解决特征检测在几何变换 (特别是尺度变化)和光学变换 下的稳定性问题,重点介绍了如何检测具有尺度不变性的特征(即"团块"或 Blob)。
1. 不变性与等变性 (Invariance & Equivariance)
在讨论特征稳定性时,我们需要区分两个概念:
- 不变性 (Invariance): 即使图像发生了变换,特征的属性(如位置、描述)保持不变。
- 等变性 (Equivariance): 如果图像发生了变换,检测到的特征也应该在对应的位置 上发生同样的变换(通常也被称为协变性)。
理想的目标: 我们希望角点位置对于光学变换 (如光照)具有不变性,而对于几何变换(如移动、旋转)具有等变性。
2. Harris 检测器的局限性分析
- 平移 (Translation): 等变。导数和窗口函数随图像移动,角点位置也随之移动。
- 旋转 (Rotation): 等变。虽然二阶矩椭圆旋转了,但其形状(由特征值决定)保持不变,因此依然能被检测为角点。
- 亮度变化 (Intensity): 部分不变。
- 对于亮度偏移 (I→I+bI \rightarrow I + bI→I+b):不变(因为导数只看变化量)。
- 对于对比度缩放 (I→aII \rightarrow aII→aI):部分不变 (如果缩放因子 aaa 太小,可能导致特征值低于阈值而被忽略)。
- 尺度 (Scale): 既不是不变的也不是等变的。这是 Harris 算子最大的弱点。
- 原因: 所有的点在微小的尺度下可能看起来像边缘,但在大尺度下可能是角点。反之,一个角点被放大后,在局部窗口内可能看起来像平坦区域或边缘。
结论: Harris 角点不具有尺度不变性。我们需要新的方法来寻找在缩放后依然稳定的特征。
3. 尺度不变性与"团块"检测 (Blob Detection)
为了解决尺度问题,我们需要找到一个特征尺度 (Characteristic Scale) ,即能够使某个函数 fff 产生局部最大值的尺度。
A. 高斯拉普拉斯 (Laplacian of Gaussian, LoG)
课件引入了 LoG 算子 作为检测工具:
- 定义: 高斯函数的二阶导数(拉普拉斯算子 ∇2g\nabla^2 g∇2g)。
- 形态: 类似于一个"墨西哥草帽",中间是正峰值,周围是负值。
- 作用: LoG 算子可以作为团块(Blob)检测器 。当 LoG 的零交叉点与圆形的边缘重合时,响应达到最大值。
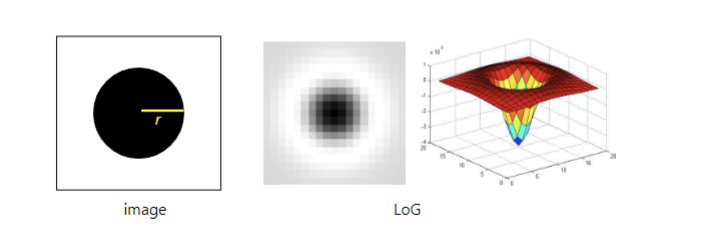
- 中间凸起 (正值): 对应团块的亮中心。
- 周围凹陷 (负值): 对应团块周围的暗背景。
- 原理: 当你拿这顶"草帽"在图像上滑动时,如果正好盖住了一个**"亮斑点"**(Blob):
- 中间的亮像素 ×\times× 草帽尖的正值 = 大正数。
- 周围的暗像素 ×\times× 草帽沿的负值 = 也是正数(负负得正)。
- 结果: 响应值瞬间爆表,达到最大。
如果你把这顶帽子盖在平坦区域或直边上,正负抵消,结果接近 0。所以,LoG 本质上就是一个专门为此形状设计的"模具"。
B. 尺度选择与归一化
如何在不同尺度下比较 LoG 响应?
- 问题: 随着尺度 σ\sigmaσ 增加(高斯核变宽),二阶导数的响应幅值会下降(因为图像被平滑得更厉害)。
- 解决方案: 尺度归一化。
- 必须将 LoG 算子乘以方差 σ2\sigma^2σ2 进行归一化。
- 归一化后的 LoG 能够消除尺度的影响,使得我们可以在尺度空间中寻找峰值。
- 特征尺度: 对于一个圆形的团块,当高斯函数的尺度 σ\sigmaσ 与团块的半径 rrr 匹配时(理论上 r=2σr = \sqrt{2}\sigmar=2 σ),归一化 LoG 的响应达到最大值。这个对应的 σ\sigmaσ 就是该特征的特征尺度 。
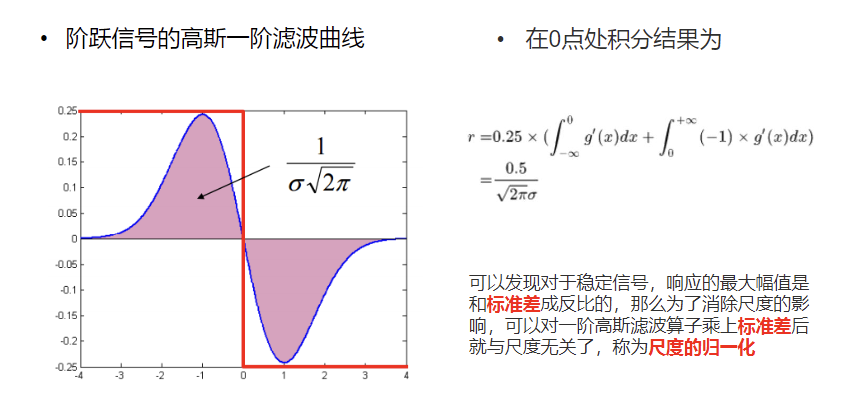
数学解释:1/σ21/\sigma^21/σ2 的衰减
从数学公式上看,这种衰减是必然的。
一维高斯函数是:
G(x,σ)=12πσe−x22σ2G(x, \sigma) = \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{x^2}{2\sigma^2}}G(x,σ)=2π σ1e−2σ2x2
如果你对它求两次导数(计算 LoG),你会发现结果中包含一个系数,它与 1σ2\frac{1}{\sigma^2}σ21 成正比。
这意味着:
-
如果不做任何处理,LoG 的响应幅度会随着 σ\sigmaσ 的平方成反比下降。
-
这就导致了一个严重的问题:大尺度的 Blob(大斑点)永远竞争不过小尺度的 Blob。 哪怕那个大斑点真的很完美,但因为检测器(σ\sigmaσ 大)本身的信号太弱,它也会被忽略。
既然响应会随着 σ2\sigma^2σ2 衰减,那我们就在计算完 LoG 之后,人为地乘回一个 σ2\sigma^2σ2。
归一化 LoG 公式:
Normalized LoG=σ2⋅(I∗LoG)\text{Normalized LoG} = \sigma^2 \cdot (I * \text{LoG})Normalized LoG=σ2⋅(I∗LoG)
这样一来
- 小尺度 (σ\sigmaσ 小):原始响应大,但乘以一个小的 σ2\sigma^2σ2,结果适中。
- 大尺度 (σ\sigmaσ 大):原始响应小,但乘以一个大的 σ2\sigma^2σ2,被拉高了。
结论:
如果不乘这个 σ2\sigma^2σ2,响应确实会随 σ\sigmaσ 增大而减小(如 PPT 所示);但为了在多尺度检测中公平地找到最大值,我们通常会使用归一化的高斯拉普拉斯算子。
特征尺度
我们将特征尺度定义为能够产生拉普拉斯响应峰值的尺度
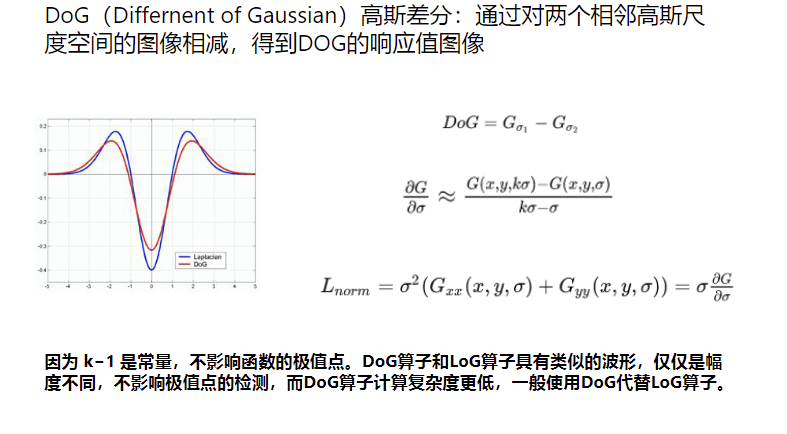
DoG 与 LoG