OpenCV(四十四)：SIFT计算描述子

SIFT 算法

SIFT（Scale-Invariant Feature Transform，尺度不变特征变换）是一种经典的局部特征提取算法，由 David Lowe 提出。SIFT 的核心目标是从图像中提取对尺度、旋转、一定光照变化和仿射变换不敏感的特征点，并为每个特征点构建一个高区分度的描述子，用于图像匹配、目标识别、三维重建等任务。

完整的 SIFT 算法流程包括四个阶段：

尺度空间极值检测（DoG）
关键点精确定位
主方向分配
关键点描述子计算

SIFT 描述子的设计思想

SIFT 描述子的核心思想是：

用关键点邻域内的局部梯度方向分布来描述该特征点。

这样做的好处是：

梯度对光照变化不敏感（相比像素值）
使用方向直方图增强旋转不变性
空间分块增强区分性和鲁棒性

最终，每个 SIFT 描述子是一个 128 维向量。

描述子计算前的准备工作

1. 坐标与尺度归一化

对于每个关键点，已知其：

位置 (x, y)
尺度 σ
主方向 θ

在计算描述子前，需要将关键点邻域：

旋转到主方向对齐
按尺度 σ 进行归一化

这样可以保证描述子对旋转和尺度变化具有不变性。

2. 邻域窗口选择

SIFT 选择关键点周围一个 16×16 的采样区域（在尺度空间中），该区域会随着关键点尺度放大或缩小。

该区域并不是简单的像素块，而是一个连续空间中按高斯加权采样的区域。

梯度计算

在关键点邻域内，对每个采样点计算：

梯度幅值
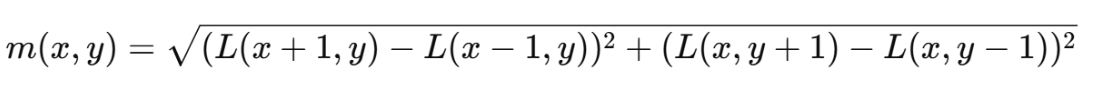
梯度方向

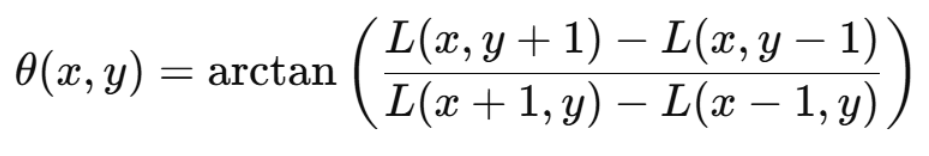
其中 L 表示高斯平滑后的图像。

在 OpenCV 中，这一步是在内部通过 Sobel 或差分方式完成的，对用户是透明的。

空间分块与方向直方图

1. 4×4 子区域划分

16×16 的邻域被划分为 4×4 个子区域，每个子区域大小约为 4×4 像素。

每个子区域单独统计梯度方向分布，这种设计兼顾了：

局部结构信息
空间布局信息

2. 8 个方向的梯度直方图

对每个子区域：

梯度方向被量化为 8 个方向区间（360° / 8 = 45°）
梯度幅值作为权重累加到对应方向

因此：

每个子区域 → 8 维向量
4×4 子区域 → 16 × 8 = 128 维

这正是 SIFT 描述子的维度来源。

高斯加权与插值

为了降低边缘噪声和量化误差，SIFT 在描述子计算中引入了两个重要机制：

1. 高斯权重

使用一个以关键点为中心的高斯函数
距离中心越远，权重越小
防止边缘像素对描述子产生过大影响

2. 三线性插值（Trilinear Interpolation）

OpenCV 的 SIFT 实现会在以下三个维度进行插值：

空间位置（x、y）
梯度方向

一个采样点的梯度能量会被分配到相邻的多个子区域和方向 bin中，从而减少量化误差，提高匹配稳定性。

描述子归一化与截断

1. L2 归一化

生成 128 维向量后，首先进行 L2 归一化：

d=d∣∣d∣∣2\mathbf{d} = \frac{\mathbf{d}}{||\mathbf{d}||_2}d=∣∣d∣∣2d

这样可以增强对整体光照变化的鲁棒性。

2. 截断（Clipping）

将向量中大于 0.2 的元素截断为 0.2
再次进行 L2 归一化

这一操作可以防止某些强梯度方向主导整个描述子，提高匹配泛化能力。

示例

python 复制代码

import cv2
import numpy as np

# 1. 读取图像（灰度图）
img = cv2.imread("test.jpg", cv2.IMREAD_GRAYSCALE)
if img is None:
    raise IOError("图像读取失败")

# 2. 创建 SIFT 对象
sift = cv2.SIFT_create(
    nfeatures=0,
    nOctaveLayers=3,
    contrastThreshold=0.04,
    edgeThreshold=10,
    sigma=1.6
)

# 3. 检测关键点并计算描述子
keypoints, descriptors = sift.detectAndCompute(img, None)

print(f"关键点数量: {len(keypoints)}")
print(f"描述子形状: {descriptors.shape}")  # (N, 128)
print(f"描述子类型: {descriptors.dtype}")   # float32

# 4. 绘制关键点
img_kp = cv2.drawKeypoints(
    img,
    keypoints,
    None,
    flags=cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS
)

cv2.imshow("SIFT Keypoints", img_kp)
cv2.waitKey(0)
cv2.destroyAllWindows()

总结

SIFT 描述子通过尺度归一化、方向对齐、空间分块和梯度方向统计，构建了一个高度稳定且区分性极强的 128 维特征向量。OpenCV 对 SIFT 的实现高度工程化，封装了复杂的数学细节，使其在计算机视觉领域长期占据重要地位。

尽管在实时性和计算成本上存在不足，但在对匹配精度和鲁棒性要求极高的场景中，SIFT 描述子仍然是一个标杆级算法。