1658. 将 x 减到 0 的最小操作数 - 力扣(LeetCode)

方法一:滑动窗口(最优解法)
思路分析:
- 计算数组的总总和 sum ,目标中间子数组的总和为
target = sum - x。- 若
target < 0:说明所有元素总和都小于 x,直接返回 - 1。 - 若
target == 0:说明需要移除所有元素,返回数组长度。
- 若
- 用滑动窗口 找中间子数组的最大长度:
- 窗口内元素总和小于
target:右指针右移,扩大窗口。 - 窗口内元素总和等于
target:记录当前窗口长度,尝试更新最大长度。 - 窗口内元素总和大于
target:左指针右移,缩小窗口。
- 窗口内元素总和小于
- 最终最少操作数 = 数组长度 - 最大窗口长度(若存在合法窗口),否则返回 - 1。
流程
-
问题转化 计算目标值:
target = sum(nums) - x- 若
target < 0:数组总和小于 x,直接返回-1(无解)
- 若
-
初始化参数
- 左指针
l = 0,右指针r = 0(窗口区间定义为[l, r),左闭右开) - 窗口内元素和
sum = 0 - 满足条件的最长子数组长度
maxLen = -1(初始为 - 1 表示无合法子数组)
- 左指针
-
滑动窗口循环 当
r ≤ 数组长度时,循环执行:- 若
sum < target:右移r,将nums[r]加入sum,直至sum ≥ target或r到数组末尾; - 若
sum > target:右移l,将nums[l]从sum中减去,直至sum ≤ target或l到数组末尾; - 若
sum == target:- 更新
maxLen = max(maxLen, r - l)(当前窗口长度为r - l) - 右移
r,让下一个元素进入窗口
- 更新
- 若
-
结果判定
- 若
maxLen ≠ -1:最少操作数 =数组长度 - maxLen,返回该值; - 若
maxLen = -1:无合法子数组,返回-1
- 若
java
class Solution {
public int minOperations(int[] nums, int x) {
int left = 0,right = 0;
int sum = 0;
int arrLength = 0,target = Arrays.stream(nums).sum() - x;
if (target == 0) {
return nums.length;
}
if(target < 0){
return -1;
}
for(;right < nums.length;right++){
sum += nums[right];
while(sum > target && left < nums.length){
sum -= nums[left++];
}
if(sum == target){
arrLength = Math.max(arrLength,right - left + 1);
}
}
return arrLength == 0 ? -1 : nums.length - arrLength;
}
}904. 水果成篮 - 力扣(LeetCode)


 、
、
这个题题目要求:虽然说了很多但是说白了就是:
找一个最长连续子数组,满足子数组中至多有两种数字。返回子数组的长度。
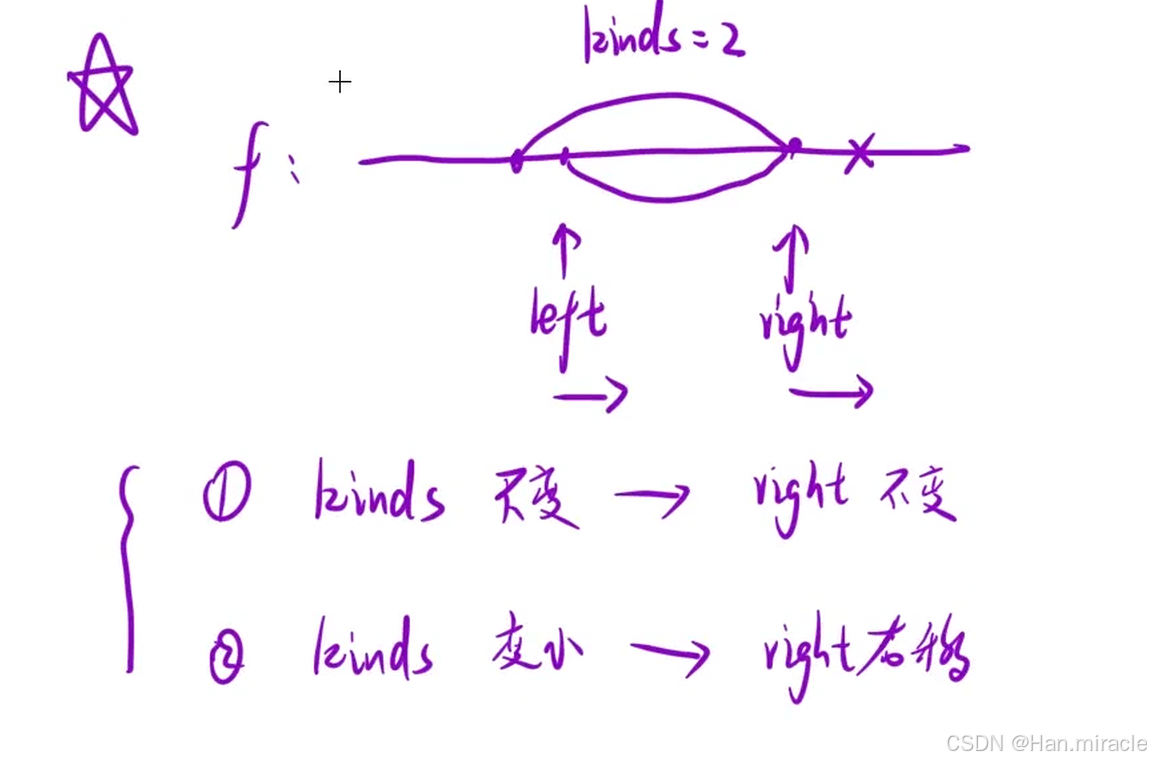
第一种暴力解法:滑动窗口 + HashMap
java
class Solution {
public int totalFruit(int[] fruits) {
int n = fruits.length;
int maxLen = 0;
int left = 0;
Map<Integer, Integer> map = new HashMap<>();
for (int right = 0; right < n; right++) {
// 将当前水果加入窗口
map.put(fruits[right], map.getOrDefault(fruits[right], 0) + 1);
// 如果窗口内水果种类超过2,移动左指针
while (map.size() > 2) {
map.put(fruits[left], map.get(fruits[left]) - 1);
if (map.get(fruits[left]) == 0) {
map.remove(fruits[left]);
}
left++;
}
// 更新最大长度
maxLen = Math.max(maxLen, right - left + 1);
}
return maxLen;
}
}暴力解法二:set
暴力枚举 + 哈希表的解法逻辑
- 遍历所有子数组的起点:从数组的第 0 个元素到最后一个元素,依次作为子数组的起点;
- 遍历子数组的终点:从起点开始,依次扩展子数组的终点;
- 用哈希表统计种类:每扩展一个元素,就将其加入哈希表,若哈希表大小(种类数)>2,则停止当前子数组的扩展;
- 记录最长长度:每次找到符合条件的子数组,更新最长长度。
java
public int totalFruit(int[] fruits) {
int maxLen = 0;
int n = fruits.length;
for (int i = 0; i < n; i++) { // 枚举子数组起点i
Set<Integer> typeSet = new HashSet<>();
for (int j = i; j < n; j++) { // 枚举子数组终点j
typeSet.add(fruits[j]);
if (typeSet.size() > 2) {
break; // 种类超过2,停止扩展
}
maxLen = Math.max(maxLen, j - i + 1); // 更新最长长度
}
}
return maxLen;
}解法三:Set + 滑动窗口
核心思路(4 步走)
1. 定义滑动窗口
用两个指针 left(左边界)、right(右边界)表示当前窗口 [left, right],窗口内的元素就是 "当前选中的水果"。
2. 扩展窗口右边界
- 遍历数组,
right逐个右移,把当前水果fruits[right]加入HashSet(Set 自动去重,仅记录 "窗口内有哪些水果种类")。
3. 校验窗口规则(核心)
- 若
Set.size() > 2(窗口内水果种类超 2 种),触发「收缩左边界」逻辑:- 临时统计:左边界水果
fruits[left]在[left+1, right]范围内的出现次数; - 若次数为 0:说明窗口剩余区域已无该水果,从 Set 中移除该种类(保证 Set.size () 准确);
- 左指针
left右移,缩小窗口,直到Set.size() ≤ 2(窗口符合规则)。
- 临时统计:左边界水果
4. 记录最大窗口长度
每次调整完窗口后,计算当前窗口长度 right - left + 1,用 maxLen 保留最大的长度(最终结果)。
通俗类比
把数组想象成一排水果摊,你用一个 "可移动的框"(窗口 [left, right])框住连续的摊位:
- 右手(
right)不断向右挪,把摊位加入框中,用一个 "种类清单"(Set)记框里有几种水果; - 若清单上水果种类超过 2 种,左手(
left)必须向右挪,挪之前先查:"当前左手边的水果,框里后面还有吗?"(统计次数);- 若没有了,就从清单上删掉这个水果;
- 不管有没有,左手都要右挪,直到清单上只剩≤2 种水果;
- 全程记录框的最大宽度(最长子数组长度)。
java
import java.util.HashSet;
import java.util.Set;
class Solution {
public int totalFruit(int[] fruits) {
int n = fruits.length;
int maxLen = 0;
int left = 0;
Set<Integer> typeSet = new HashSet<>(); // 仅记录窗口内的水果种类
for (int right = 0; right < n; right++) {
// 1. 将当前水果加入种类集合
typeSet.add(fruits[right]);
// 2. 若种类超过2种,收缩左边界
while (typeSet.size() > 2) {
// 临时统计:左边界水果在 [left+1, right] 中的出现次数
int count = 0;
for (int i = left + 1; i <= right; i++) {
if (fruits[i] == fruits[left]) {
count++;
}
}
// 若剩余次数为0,说明窗口内无该水果,从Set移除
if (count == 0) {
typeSet.remove(fruits[left]);
}
// 左指针右移,缩小窗口
left++;
}
// 3. 更新最长窗口长度
maxLen = Math.max(maxLen, right - left + 1);
}
return maxLen;
}
// 测试示例
public static void main(String[] args) {
Solution solution = new Solution();
int[] fruits = {1,2,3,2,2};
System.out.println(solution.totalFruit(fruits)); // 输出4
}
}关键逻辑补充
- 窗口定义 :
[left, right]为当前窗口,保证窗口内水果种类 ≤ 2 种; - Set 的作用 :仅判断 "窗口内有多少种水果"(
set.size()),不记录次数; - 窗口扩展 :右指针
right遍历数组,将当前水果加入 Set; - 窗口收缩 :若
set.size() > 2,需移动左指针left,临时统计左边界水果在窗口内的剩余次数 ,当次数为 0 时从 Set 中移除该种类,直到set.size() ≤ 2; - 更新最大长度:每次调整完窗口后,记录窗口的最大长度。
解法四:map+滑动窗口
1. 问题核心
需找到数组中连续、种类≤2 种的最长子数组,本质是 "子数组种类限制" 类问题,滑动窗口是最优解法,HashMap 用于辅助统计窗口内关键信息。
2. 滑动窗口定义
用双指针left(左)、right(右)表示窗口[left, right],窗口内元素为当前待校验的子数组:
right:主动扩展,遍历数组所有元素,探索更大的窗口;left:被动收缩,仅当窗口违反 "种类≤2" 规则时右移,保证窗口合法性。
3. HashMap 的作用
键为水果种类,值为该种类在窗口内的出现次数:
- 扩展窗口时:更新当前水果的次数(存在则 + 1,不存在则初始化为 1);
- 收缩窗口时:减少左边界水果的次数,次数为 0 则移除该种类(保证
map.size()精准反映窗口内种类数); - 规则校验:通过
map.size()直接判断窗口内种类是否超过 2 种。
4. 完整执行流程
- 初始化:
left=0、maxLen=0(最长长度)、空 HashMap; - 遍历数组(
right从 0 到数组末尾):- 把
fruits[right]加入 HashMap,更新次数; - 若
map.size()>2,循环收缩左边界:fruits[left]次数 - 1,次数为 0 则从 Map 中移除;left右移;
- 计算当前窗口长度
right-left+1,更新maxLen为最大值;
- 把
- 返回
maxLen。
5. 性能逻辑
- 时间复杂度 O (n):每个元素仅被
left和right各遍历一次,无重复操作; - 空间复杂度 O (1):HashMap 最多存储 2 种水果的次数,空间消耗固定。
java
import java.util.HashMap;
import java.util.Map;
class Solution {
public int totalFruit(int[] fruits) {
int n = fruits.length;
int maxLen = 0; // 最长符合条件的子数组长度
int left = 0; // 窗口左指针
// key:水果种类,value:该种类在窗口内的出现次数
Map<Integer, Integer> fruitCountMap = new HashMap<>();
// 扩展右边界
for (int right = 0; right < n; right++) {
int currFruit = fruits[right];
// 更新当前水果的次数(存在则+1,不存在则初始化为1)
fruitCountMap.put(currFruit, fruitCountMap.getOrDefault(currFruit, 0) + 1);
// 种类超2,收缩左边界
while (fruitCountMap.size() > 2) {
int leftFruit = fruits[left];
// 左边界水果次数-1
fruitCountMap.put(leftFruit, fruitCountMap.get(leftFruit) - 1);
// 次数为0则移除该种类,保证size()准确
if (fruitCountMap.get(leftFruit) == 0) {
fruitCountMap.remove(leftFruit);
}
left++; // 左指针右移
}
// 更新最长窗口长度
maxLen = Math.max(maxLen, right - left + 1);
}
return maxLen;
}
// 测试示例
public static void main(String[] args) {
Solution solution = new Solution();
int[] fruits = {1,2,3,2,2};
System.out.println(solution.totalFruit(fruits)); // 输出4
}
}