算法-动态规划-13

力扣-真题-最大正方形

对于这道题，题目要求找到二维矩阵内的最大正方形。

我们可以转化一下问题 ,

我们定义 f[m][n] 是以 val[m][n]作为右下角的最大的正方形。

如果 val[0][0] 的值是 '1' 时， f[0][0] 为 1 ；

而且对于 m = 0 或者 n = 0 的 f[m][n] 当其 val[m][n]值为 '1' 时都有

f[m][n] = 1 ;

上面就是我们已知的条件了，那么我们要怎么计算后续的f[m][n]呢？

我们从 f[1][1]开始，

f[1][1] 如果是 0 ，那么 val[1][1] 一定等于 '0'

如果是 1 ，那么 val[1][1] 等于 '1' ， val[1[0],val[0][1],val[0][0]肯定有一个等于 '0', 此时 f[1][0], f[0][1], f[0][0]其中一个为 '0'

如果是 2 ，那么 val[1[0],val[0][1],val[0][0],val[1][1] 的值都为'1'

f[1][0 ], f[0][1], f[0][0]肯定都为1 。

也就是说f[m][n]的值跟 f[m-1][n], f[m][n-1], f[m-1][n-1]有关。

首先两种情况一种情况是 val[m][n]是 '0' 所以 f[m][n]肯定为0 。

另一种情况，则是根据 f[m-1][n], f[m][n-1], f[m-1][n-1]进行计算。

针对三个值，进行分析。

如果存在一个是 0 ，那么 f[m][n] = 1

如果都大于 0，存在一个是'1' ， f[m][n] 好像只有可能是 2 ，因为都大于0 ，所以至少是1 ，那么 f[m][n]等于2 就满足条件了。

那么f[m][n]可能等于3吗？等于3的条件好像周边三个值f[][]都得至少为2 ，因为存在一个等于1

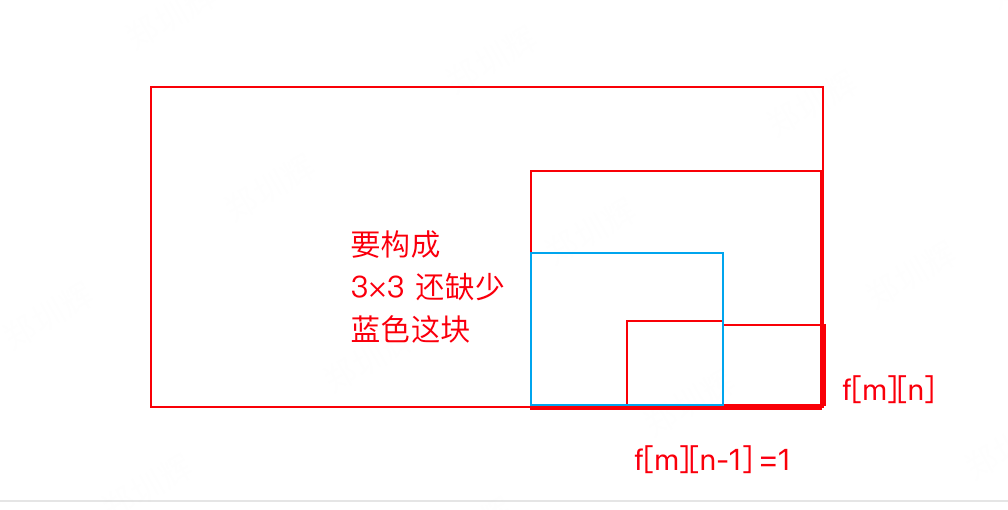
那么往下推， f[m][n]的值，跟 f[m-1][n], f[m][n-1], f[m-1][n-1]中的最小值，假如说是 x , 那么其值就是x +1 。

java 复制代码

public int maximalSquare(char[][] matrix) {
        int max = 0;
        int[][] f = new int[matrix.length][matrix[0].length];
        for (int i = 0; i < matrix.length; i++) {
            if (matrix[i][0] == '1') {
                f[i][0] = 1;
                max = 1;
            }
        }

        for (int i = 0; i < matrix[0].length; i++) {
            if (matrix[0][i] == '1') {
                f[0][i] = 1;
                max = 1;
            }
        }


        for (int i = 1; i < matrix.length; i++) {
            for (int j = 1; j < matrix[0].length; j++) {
                if (matrix[i][j] == '1') {
                    int min = Math.min(f[i - 1][j], f[i][j - 1]);
                    min = Math.min(min, f[i - 1][j - 1]);
                    f[i][j] = min + 1;
                    max = Math.max(max, f[i][j]);
                } else {
                    f[i][j] = 0;
                }
            }
        }

        return max * max;
    }

复杂度

时间复杂度分析

初始化第一列：遍历 matrix 的行数，执行 m 次操作

初始化第一行：遍历 matrix 的列数，执行 n 次操作

填充DP表：嵌套循环遍历从 (1,1) 到 (m-1,n-1) 的每个位置，执行 (m-1)*(n-1) 次操作

总的操作次数约为 m + n + (m-1)(n-1) = O(mn)，因此时间复杂度确实是 O(mn)。

空间复杂度分析

主要的空间消耗来自创建的二维数组 f：

f 数组大小为 m × n，存储了每个位置的最大正方形边长

其他变量如 max、min 等都是常量空间

所以空间复杂度也是 O(mn)。