更多内容:XiaoJ的知识星球
目录
- Matcha-TTS:一种带条件流程匹配的快速TTS架构
- 1.介绍
- 2.背景
-
- [2.1 近期的编码器-解码器TTS架构](#2.1 近期的编码器-解码器TTS架构)
- [2.2 流匹配与TTS](#2.2 流匹配与TTS)
- 3.方法
-
- [3.1 OT-CFM(解释部分)](#3.1 OT-CFM(解释部分))
-
- [1)公式1: 常微分方程(ODE)](#1)公式1: 常微分方程(ODE))
- [2)公式2: 流匹配损失(FM)](#2)公式2: 流匹配损失(FM))
- [3)公式3: 条件流匹配损失(CFM)](#3)公式3: 条件流匹配损失(CFM))
- [4)公式4: OT-CFM损失(最优传输版本)](#4)公式4: OT-CFM损失(最优传输版本))
- [3.1 OT-CFM(原义)](#3.1 OT-CFM(原义))
- [3.2 提出的架构](#3.2 提出的架构)
- 参考:
Matcha-TTS:一种带条件流程匹配的快速TTS架构
Matcha-TTS是一种用于快速TTS声学建模的新型编码-解码器架构,采用最优传输条件流匹配(OT-CFM)训练。
-
这使得基于常微分方程的译码器能够在更少的合成步骤内实现高输出质量,而非使用分数匹配训练的模型。
-
精心设计的选择还确保了每个合成步骤的快速运行。
-
该方法具有概率性、非自回归性,并且能够从零开始学习在没有外部对齐的情况下进行交流。
-
与强力的预训练基线模型相比,Matcha-TTS系统内存占用最小,在长语句上速度可媲美最快模型,并在听力测试中获得最高的平均意见分数。
.
1.介绍
扩散概率模型 (DPMs,Diffusion probabilistic models)是当前生成模型领域的新标准,特别擅长生成图像、动作、语音等连续数据。其核心原理很简单:
-
先通过逐步加噪将真实数据"破坏"成纯噪声,如高斯噪声;
-
然后训练模型学会从噪声"重建"出原始数据。
这个重建过程可以用两种数学方式描述:
-
随机性的随机微分方程 (SDEs,stochastic differential equations),每次生成结果略有不同;
-
确定性的常微分方程 (ODE,ordinary differential equation),称为概率流ODE(probability flow ODE),它能从相同噪声生成完全相同的结果,且计算效率更高。
概率流ODE就像一个精确的导航系统:给定一个噪声起点,它能确定性地将你引导到清晰的数据终点。相比传统方法,如连续时间归一化流(CNF,continuous-time normalising flows),它不需要复杂的训练技巧,就能高效生成高质量数据。
DPM的SDE训练核心在于得分函数 (score function)------即数据分布对数概率密度的梯度。其训练特点如下:
训练方式:通过均方误差(MSE)目标函数来近似分数函数,这一目标可从似然的证据下界(ELBO)推导而来
显著优势:
-
训练过程快速简单,无需数值SDE/ODE求解器参与
-
与传统归一化流模型不同,不限制模型架构设计,为网络结构提供更大灵活性
核心瓶颈:(合成速度慢,这是DPMs长期面临的主要实践挑战)
-
每个样本生成需要大量迭代步骤(通常数百步);
-
每一步都必须顺序计算,无法并行化;
-
每个步骤都需要完整评估整个神经网络,计算开销巨大
这种"训练快、生成慢"的特性形成了鲜明对比:虽然DPMs在训练阶段高效灵活,但实际应用时的生成效率问题成为制约其广泛部署的关键因素。
Matcha-TTS,这是一个基于连续归一化流的概率性、非自回归、快速采样自TTS的声学模型。 主要有两项创新:
(1)采用1D CNN 与Transformer 混合的编码器-解码器架构。而且还显著降低内存消耗,提升模型评估速度
(2)使用最优传输条件流匹配 (OT-CFM,optimal-transport conditional flow matching)训练模型:
-
这是一种学习从数据分布中采样的常微分方程的新方法。
-
与传统CNF和评分匹配概率流常微分方程相比,OT-CFM定义了从源(噪声)到目标(数据)的更简易路径,使得比DPM更少的步骤实现准确合成。
实验表明,这两项创新都加快了合成速度,减少了速度与合成质量之间的权衡。尽管速度快且轻便,Matcha-TTS学会说话和对齐,无需外部矫正器。与强大的预训练基线模型相比,Matcha-TTS实现了快速的合成和更好的自然性评分。音频示例和代码在 https://shivammehta25.github.io/Matcha-TTS/
.
2.背景
2.1 近期的编码器-解码器TTS架构
扩散概率模型(DPMs)已应用于众多语音合成任务中,并取得了令人印象深刻的结果,包括波形生成和端到端TTS。Diff-TTS首次将DPMs应用于声学建模。随后,Grad-TTS将扩散过程概念化为随机微分方程(SDE)。尽管这些模型以及其衍生模型如Fast Grad-TTS是非自回归的,但TorToiSe展示了在具有量化潜变量的自回归TTS模型中应用DPMs的效果。
上述模型------与许多现代TTS声学模型一样------采用编码器-解码器架构,编码器中使用Transformer模块。
-
许多模型(如FastSpeech 1和2)使用正弦位置嵌入来处理位置依赖关系。然而,研究发现这种方法在长序列上的泛化能力较差;
-
Glow-TTS、VITS和Grad-TTS则采用相对位置嵌入。不幸的是,这些方法将短上下文窗口之外的输入视为"词袋",通常导致不自然的韵律。
-
LinearSpeech转而采用旋转位置嵌入 (RoPE),与相对嵌入相比,RoPE在计算和内存方面具有优势,并且能够更好地泛化到更长的距离。
因此,Matcha-TTS在编码器中使用带有RoPE的Transformer,相比Grad-TTS减少了内存使用。这应该是首个在基于SDE或ODE的TTS方法中使用RoPE的工作。
现代TTS架构在解码器网络设计方面也存在差异。
-
基于归一化流的方法Glow-TTS和OverFlow使用膨胀一维卷积。
-
基于DPM(扩散概率模型)的方法使用一维卷积来合成梅尔频谱图。
-
Grad-TTS使用带有二维卷积的U-Net网络。这种方法将梅尔频谱图视为图像,并隐含地假设在时间和频率两个维度上都具有平移不变性。然而,语音的梅尔频谱在频率轴上并不完全具有平移不变性,而且二维解码器通常需要更多内存,因为它们在张量中引入了额外的维度。
-
同时,像FastSpeech 1和2这样的非概率模型已经证明,使用 1D Transformer 的解码器能够学习长距离依赖关系并实现快速、并行的合成。
Matcha-TTS在解码器中使用Transformer,但采用了 1D U-Net 设计,该设计受到Stable Diffusion图像生成模型中 2D U-Net 的启发。
虽然一些TTS系统(如FastSpeech)依赖于外部提供的对齐信息,但大多数系统能够同时学习说话和对齐能力,尽管研究发现鼓励或强制执行单调对齐对于快速有效的训练至关重要。实现这一目标的一种机制是单调对齐搜索(MAS),该机制被Glow-TTS和VITS等系统所采用。特别是,Grad-TTS使用了一种基于MAS的机制,他们称之为先验损失(prior loss),以快速学习将输入符号与输出帧对齐。这些对齐信息还用于训练一个确定性时长预测器,该预测器在对数域中最小化均方误差(MSE)。Matcha-TTS在对齐和时长建模方面采用了相同的这些方法。最后,Matcha-TTS的不同之处,在于在所有解码器前馈层中使用了来自BigVGAN的snake beta激活函数。
.
2.2 流匹配与TTS
目前,一些最高质量的TTS系统要么利用扩散概率模型(DPMs),要么使用离散时间归一化流,而连续时间流的研究相对较少。
Lipman等人最近提出了一种使用常微分方程(ODEs)进行合成的框架,该框架统一并扩展了概率流ODEs和连续归一化流(CNFs)。随后,他们提出了一种高效的学习ODEs用于合成的方法,使用一种称为条件流匹配 (CFM)的简单向量场回归损失,作为学习DPMs的评分函数或在训练时使用数值ODE求解器(如经典CNFs)的替代方案。
关键的是,通过利用最优传输的思想,CFM可以被设置为产生具有简单向量场的ODEs,这些向量场在将样本从源分布映射到数据分布的过程中变化很小,因为它本质上只是沿着直线传输概率质量。这种技术被称为OT-CFM;校正流(rectified flows)代表了具有类似思想的同期工作。这些简单的路径意味着ODE可以使用较少的离散化步骤被精确求解,即与DPMs相比,可以在更少的神经网络评估次数下绘制出精确的模型样本,从而在相同质量下实现更快的合成速度。
CFM是一种新技术,与早期加速基于SDE/ODE的TTS方法不同,后者通常基于知识蒸馏。在Matcha-TTS之前,唯一公开的关于基于CFM的声学建模的预印本是Meta的Voicebox模型。Voicebox(VB)是一个基于大规模训练数据执行各种文本引导语音填充任务的系统,其英文变体(VB-En)在6万小时的专有数据上进行训练。
VB与Matcha-TTS存在显著差异:VB执行TTS、去噪和文本引导声学填充任务,使用掩码和CFM相结合的方式进行训练,而Matcha-TTS是一个纯粹的TTS模型,仅使用OT-CFM进行训练。VB使用带有AliBi自注意力偏置的卷积位置编码,而Matcha-TTS的文本编码器使用RoPE。与VB不同,Matcha-TTS在标准数据上进行训练,并公开提供代码和模型检查点。VB-En消耗3.3亿个参数,这比实验中的Matcha-TTS模型大18倍。此外,VB使用外部对齐进行训练,而Matcha-TTS无需外部对齐即可学习说话。
.
3.方法
下面将介绍两个内容:
-
一是最优传输条件流匹配(**OT-CFM,**Optimal-transport conditional flow matching),为方便理解,这部分内容将分为(解释部分+原义)
-
提出的架构(Proposed architecture)
.
3.1 OT-CFM(解释部分)
最优传输条件流匹配(OT-CFM) 是一种生成模型的训练方法。下面介绍一些概念,然后将会对公式进行说明:
概率密度路径 (公式中的 p t p_t pt)
想象你有一堆数据点(比如图片),它们分布在空间中。 p t p_t pt 就是一条"路径",描述了如何从一个简单的分布(比如标准正态分布)逐渐变化到复杂的数据分布。
-
p 0 ( x ) p_0(x) p0(x) : 起点,是简单的标准正态分布 N ( x ; 0 , I ) \mathcal{N}(x; \mathbf{0}, I) N(x;0,I)
-
p 1 ( x ) p_1(x) p1(x) : 终点,是复杂的数据分布 q ( x ) q(x) q(x)
-
t ∈ [ 0 , 1 ] t \in [0,1] t∈[0,1] : 时间参数, t = 0 t=0 t=0 时是起点, t = 1 t=1 t=1 时是终点
向量场 (公式中的 v t \mathbf{v}_t vt 和 u t \mathbf{u}_t ut)
向量场就像"风向图",告诉每个点在每个时间 t t t 应该往哪个方向移动。
-
v t ( x ; θ ) \mathbf{v}_t(x; \theta) vt(x;θ): 我们要训练的神经网络,预测每个点的移动方向
-
u t ( x ) \mathbf{u}_t(x) ut(x): 理想的、正确的移动方向(我们想让神经网络学会这个)
1)公式1: 常微分方程(ODE)
d d t ϕ t ( x ) = v t ( ϕ t ( x ) ) ; ϕ 0 ( x ) = x \frac{d}{dt} \phi_t(x) = \mathbf{v}_t(\phi_t(x)); \quad \phi_0(x) = x dtdϕt(x)=vt(ϕt(x));ϕ0(x)=x
通俗解释:
-
ϕ t ( x ) \phi_t(x) ϕt(x) 表示一个点 x x x 在时间 t t t 的位置
-
这个公式说:点的位置变化速度 = 当前位置的向量场值
-
就像一艘船在河流中航行,河流的流速(向量场)决定了船的移动轨迹
实际应用 :如果我们知道向量场 v t \mathbf{v}_t vt,就能通过解这个方程,把简单的噪声( t = 0 t=0 t=0)变成复杂的数据( t = 1 t=1 t=1)。
2)公式2: 流匹配损失(FM)
L FM ( θ ) = E t , p t ( x ) ∥ u t ( x ) − v t ( x ; θ ) ∥ 2 \mathcal{L}{\text{FM}}(\theta) = \mathbb{E}{t, p_t(x)} \left\| \mathbf{u}_t(x) - \mathbf{v}_t(x; \theta) \right\|^2 LFM(θ)=Et,pt(x)∥ut(x)−vt(x;θ)∥2
通俗解释:
-
这是训练神经网络的目标函数
-
意思是:让神经网络预测的移动方向 v t \mathbf{v}_t vt 尽可能接近正确的移动方向 u t \mathbf{u}_t ut
-
E t , p t ( x ) \mathbb{E}_{t, p_t(x)} Et,pt(x) 表示在所有时间点 t t t 和所有位置 x x x 上取平均
-
∥ ⋅ ∥ 2 \left\| \cdot \right\|^2 ∥⋅∥2 是平方误差,衡量两个向量的差距
问题 :实际中我们不知道真实的 u t \mathbf{u}_t ut 和 p t ( x ) p_t(x) pt(x),所以这个损失无法直接计算。
3)公式3: 条件流匹配损失(CFM)
L CFM ( θ ) = E t , q ( x 1 ) , p 0 ( x 0 ) ∥ u t ( x 1 ) − v t ( x ; θ ) ∥ 2 \mathcal{L}{\text{CFM}}(\theta) = \mathbb{E}{t, q(x_1), p_0(x_0)} \left\| \mathbf{u}_t(x_1) - \mathbf{v}_t(x; \theta) \right\|^2 LCFM(θ)=Et,q(x1),p0(x0)∥ut(x1)−vt(x;θ)∥2
改进点:
-
不再需要知道 p t ( x ) p_t(x) pt(x),而是直接使用:
-
q ( x 1 ) q(x_1) q(x1): 真实数据分布(我们有的数据)
-
p 0 ( x 0 ) p_0(x_0) p0(x0): 简单的标准正态分布(我们可以生成的噪声)
-
-
u t ( x 1 ) \mathbf{u}_t(x_1) ut(x1): 给定终点 x 1 x_1 x1 时的条件向量场
关键优势:这个损失可以实际计算!因为我们有真实数据,也能生成噪声。
4)公式4: OT-CFM损失(最优传输版本)
L ( θ ) = E t , q ( x 1 ) , p 0 ( x 0 ) ∥ u t OT ( ϕ t OT ( x ) ∣ x 1 ) − v t ( ϕ t OT ( x ) ; μ ) ∥ 2 \mathcal{L}(\theta) = \mathbb{E}_{t, q(x_1), p_0(x_0)} \left\| \mathbf{u}_t^{\text{OT}}(\phi_t^{\text{OT}}(x) | x_1) - \mathbf{v}_t(\phi_t^{\text{OT}}(x); \mu) \right\|^2 L(θ)=Et,q(x1),p0(x0) utOT(ϕtOT(x)∣x1)−vt(ϕtOT(x);μ) 2
最优传输的核心思想:
-
为每个真实数据点 x 1 x_1 x1 随机匹配一个噪声点 x 0 x_0 x0
-
定义一条直线路径 : ϕ t OT ( x ) = ( 1 − ( 1 − σ min ) t ) x 0 + t x 1 \phi_t^{\text{OT}}(x) = (1 - (1 - \sigma_{\text{min}})t)x_0 + t x_1 ϕtOT(x)=(1−(1−σmin)t)x0+tx1
-
这条路径是最优的,因为两点之间直线最短
目标向量场 : u t OT ( ϕ t OT ( x 0 ) ∣ x 1 ) = x 1 − ( 1 − σ min ) x 0 \mathbf{u}t^{\text{OT}}(\phi_t^{\text{OT}}(x_0) | x_1) = x_1 - (1 - \sigma{\text{min}})x_0 utOT(ϕtOT(x0)∣x1)=x1−(1−σmin)x0
实际应用中的意义
以 Matcha-TTS(语音合成模型)为例:
训练时:
-
从语音数据中随机选一个真实语音片段 x1
-
生成一个随机噪声 x0(标准正态分布)
-
用直线连接它们,得到中间状态 ϕtOT(x)
-
让神经网络预测从当前状态到目标状态的方向
-
用公式(4)的损失函数训练网络
生成时(语音合成):
-
从噪声 x0 开始
-
用训练好的神经网络预测移动方向
-
沿着预测的方向一步步移动(解ODE)
-
最终得到高质量的语音 x1
.
3.1 OT-CFM(原义)
在此对流匹配方法进行高层次概述,首先介绍由向量场生成的概率密度路径,然后推导出OT-CFM目标函数。
设 x x x 表示从复杂且未知的数据分布 q ( x ) q(x) q(x) 中采样的数据空间 R d \mathbb{R}^d Rd 中的一个观测值。概率密度路径 ( p t : [ 0 , 1 ] × R d → R p_t: [0,1] \times \mathbb{R}^d \to \mathbb{R} pt:[0,1]×Rd→R)是一个随时间变化的概率密度函数,其中 t ∈ [ 0 , 1 ] t \in [0,1] t∈[0,1],且 p 1 ( x ) = q ( x ) p_1(x) = q(x) p1(x)=q(x)。一种从数据分布 q q q 生成样本的方法是构建一个概率路径 p t p_t pt,使得当 t ∈ [ 0 , 1 ] t \in [0,1] t∈[0,1] 时, p 0 ( x ) = N ( x ; 0 , I ) p_0(x) = \mathcal{N}(x; \mathbf{0}, I) p0(x)=N(x;0,I) 是一个先验分布,且 p 1 ( x ) p_1(x) p1(x) 逼近数据分布 q ( x ) q(x) q(x)。例如,CNFs(连续归一化流)首先定义一个向量场 v t : [ 0 , 1 ] × R d → R d \mathbf{v}_t: [0,1] \times \mathbb{R}^d \to \mathbb{R}^d vt:[0,1]×Rd→Rd,该向量场通过以下常微分方程生成流 ϕ t : [ 0 , 1 ] × R d → R d \phi_t: [0,1] \times \mathbb{R}^d \to \mathbb{R}^d ϕt:[0,1]×Rd→Rd:
d d t ϕ t ( x ) = v t ( ϕ t ( x ) ) ; ϕ 0 ( x ) = x . (1) \frac{d}{dt} \phi_t(x) = \mathbf{v}_t(\phi_t(x)); \quad \phi_0(x) = x. \tag{1} dtdϕt(x)=vt(ϕt(x));ϕ0(x)=x.(1)
这生成了路径 p t p_t pt,作为数据点的边缘概率分布。可以通过求解方程 (1) 中的初始值问题,从近似的数据分布 p 1 p_1 p1 中采样。
假设存在一个已知的向量场 u t \mathbf{u}_t ut,它能生成从 p 0 p_0 p0 到 p 1 ≈ q p_1 \approx q p1≈q 的概率路径 p t p_t pt。流匹配损失定义为:
L FM ( θ ) = E t , p t ( x ) ∥ u t ( x ) − v t ( x ; θ ) ∥ 2 , (2) \mathcal{L}{\text{FM}}(\theta) = \mathbb{E}{t, p_t(x)} \left\| \mathbf{u}_t(x) - \mathbf{v}_t(x; \theta) \right\|^2, \tag{2} LFM(θ)=Et,pt(x)∥ut(x)−vt(x;θ)∥2,(2)
其中 t ∼ U [ 0 , 1 ] t \sim \mathcal{U}[0,1] t∼U[0,1], v t ( x ; θ ) \mathbf{v}_t(x; \theta) vt(x;θ) 是一个参数为 θ \theta θ 的神经网络。尽管如此,流匹配在实际应用中难以处理,因为通常无法直接获取向量场 u t \mathbf{u}_t ut 和目标概率 p t p_t pt。因此,条件流匹配转而考虑:
L CFM ( θ ) = E t , q ( x 1 ) , p 0 ( x 0 ) ∥ u t ( x 1 ) − v t ( x ; θ ) ∥ 2 . (3) \mathcal{L}{\text{CFM}}(\theta) = \mathbb{E}{t, q(x_1), p_0(x_0)} \left\| \mathbf{u}_t(x_1) - \mathbf{v}_t(x; \theta) \right\|^2. \tag{3} LCFM(θ)=Et,q(x1),p0(x0)∥ut(x1)−vt(x;θ)∥2.(3)
这将难以处理的边缘概率密度和向量场替换为条件概率密度和条件向量场。关键的是,这些在一般情况下是可处理的,并且具有闭式解;此外可以进一步证明, L CFM ( θ ) \mathcal{L}{\text{CFM}}(\theta) LCFM(θ) 和 L FM ( θ ) \mathcal{L}{\text{FM}}(\theta) LFM(θ) 关于 θ \theta θ 具有相同的梯度。
Matcha-TTS 使用最优传输条件流匹配(OT-CFM)进行训练,这是流匹配的一种变体,具有特别简单的梯度。OT-CFM 损失函数可表示为:
L ( θ ) = E t , q ( x 1 ) , p 0 ( x 0 ) ∥ u t OT ( ϕ t OT ( x ) ∣ x 1 ) − v t ( ϕ t OT ( x ) ; μ ) ∥ 2 , (4) \mathcal{L}(\theta) = \mathbb{E}_{t, q(x_1), p_0(x_0)} \left\| \mathbf{u}_t^{\text{OT}}(\phi_t^{\text{OT}}(x) | x_1) - \mathbf{v}_t(\phi_t^{\text{OT}}(x); \mu) \right\|^2, \tag{4} L(θ)=Et,q(x1),p0(x0) utOT(ϕtOT(x)∣x1)−vt(ϕtOT(x);μ) 2,(4)
其中定义 ϕ t OT ( x ) = ( 1 − ( 1 − σ min ) t ) x 0 + t x 1 \phi_t^{\text{OT}}(x) = (1 - (1 - \sigma_{\text{min}})t)x_0 + t x_1 ϕtOT(x)=(1−(1−σmin)t)x0+tx1 为从 x 0 x_0 x0 到 x 1 x_1 x1 的流,其中每个数据点 x 1 x_1 x1 与从随机样本 x 0 ∼ N ( 0 , I ) x_0 \sim \mathcal{N}(\mathbf{0}, I) x0∼N(0,I) 中匹配的样本配对。其梯度向量场(即学习目标)为 u t OT ( ϕ t OT ( x 0 ) ∣ x 1 ) = x 1 − ( 1 − σ min ) x 0 \mathbf{u}t^{\text{OT}}(\phi_t^{\text{OT}}(x_0) | x_1) = x_1 - (1 - \sigma{\text{min}})x_0 utOT(ϕtOT(x0)∣x1)=x1−(1−σmin)x0。这些性质使得训练更简单、更快,生成速度更快,且性能优于 DPMs(扩散概率模型)。
.
3.2 提出的架构
图 1:合成时所提出的方法概览
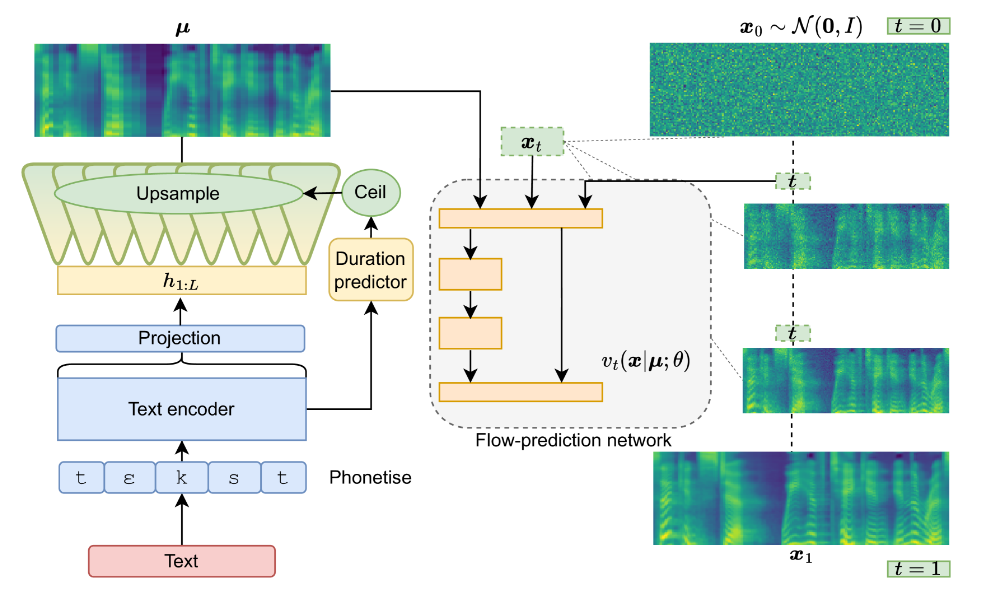
Matcha-TTS是一种用于神经语音合成(TTS)的非自回归编码器-解码器架构。上图提供了该架构的概览。文本编码器和时长预测器的架构,但使用旋转位置嵌入替代了相对位置嵌入。对齐和时长模型的训练使用MAS(单调对齐搜索)以及先验损失ℒenc。
预测的时长(向上取整)用于上采样(复制)编码器输出的向量,从而获得𝝁,即给定文本和所选时长条件下预测的平均声学特征(例如,梅尔频谱图)。该均值用于调节解码器,该解码器预测用于合成的向量场 v t ( ϕ t O T ( x 0 ) ∣ μ ; θ ) \mathbf{v}_t(\phi_t^{OT}(x_0)|\mu; \theta) vt(ϕtOT(x0)∣μ;θ),但不作为初始噪声样本𝒙₀的均值(与Grad-TTS不同)。
图 2:Matcha-TTS解码器(图1中的flow-prediction network)
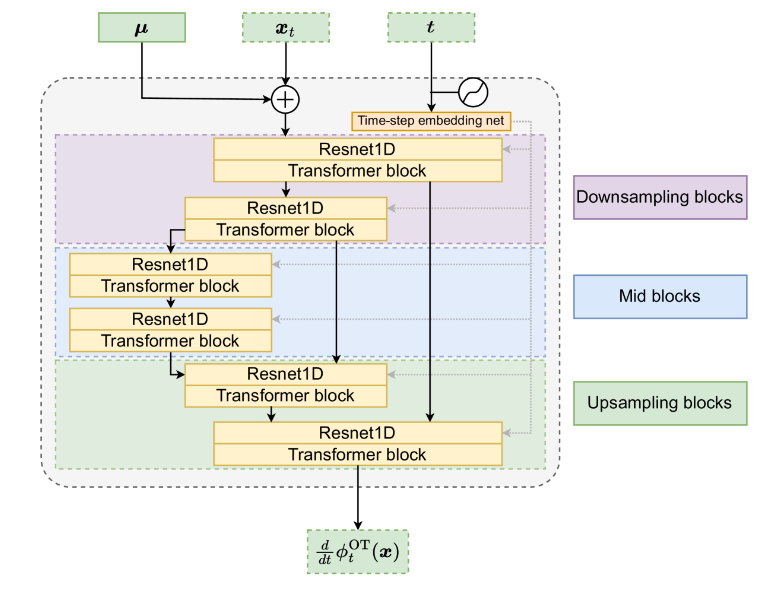
上图展示了Matcha-TTS解码器架构。它是一个包含一维卷积残差块的U-Net,用于对输入进行下采样和上采样,并嵌入了流匹配步骤𝑡∈[0,1]。每个残差块后跟一个Transformer块,其前馈网络使用snake beta激活函数。这些Transformer不使用任何位置嵌入,因为音素间的位置信息已经由编码器处理,而卷积和下采样操作则用于在同一音素内对帧间进行插值,并区分它们之间的相对位置。与Grad-TTS使用的纯2D卷积U-Net相比,该解码器网络评估速度显著更快,且内存消耗更少。
.
接下来就是论文中的实验与简单总结,感兴趣请阅读原文。
.
参考:
.
声明:资源可能存在第三方来源,若有侵权请联系删除!