此分类用于记录吴恩达深度学习课程的学习笔记。
课程相关信息链接如下:
- 原课程视频链接:[双语字幕]吴恩达深度学习deeplearning.ai
- github课程资料,含课件与笔记:吴恩达深度学习教学资料
- 课程配套练习(中英)与答案:吴恩达深度学习课后习题与答案
本周为第四课的第三周内容,这一课所有内容的中心只有一个:计算机视觉 。应用在深度学习里,就是专门用来进行图学习的模型和技术,是在之前全连接基础上的"特化",也是相关专业里的一个重要研究大类。
这一整节课都存在大量需要反复理解的内容和机器学习、数学基础。 因此我会尽可能的补足基础,用比喻和实例来演示每个部分,从而帮助理解。
第三周的内容将从图像分类 进一步拓展到目标检测(Object Detection) 这一更具挑战性的计算机视觉任务。
与分类任务只需回答"图中有什么"不同,目标检测需要同时解决" 有什么 "以及"在什么位置 "两个问题,因此在模型结构设计、训练方式和评价标准上都更为复杂。
本篇的内容关于交并比、非极大值抑制和锚框,是对上一篇目标检测算法对的一些补充。
1.交并比(Intersection over Union,IoU)
在分类任务中,我们介绍过一些评估指标来评估分类模型的性能,现在当任务从分类发展到检测,自然也要有相应的评估指标来评估"定位的准不准"以及"有多准"。
因此,交并比就是我们针对目标检测任务而定义的评估指标,它的字面意思是"交集面积除以并集面积",用于衡量两个边界框的重叠程度 。
这个概念并不难理解,我们来看课程中里例子:
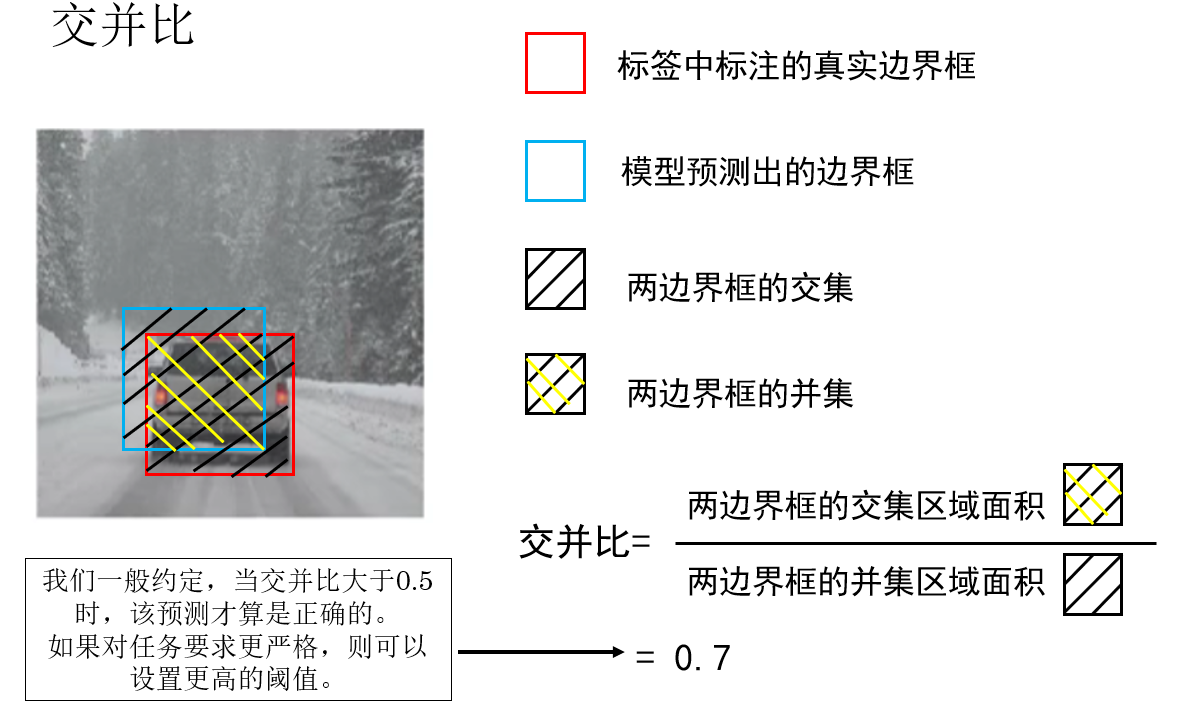
很显然,交并比越大,就代表我们预测的目标位置越接近真实值,模型的效果就越好:
- \(IoU = 0\):完全不重叠
- \(IoU = 1\):完全重合
并且,不同于之前我们使用的准确率,F1 分数等指标仅仅用作评估,我们还可以依靠交并比进一步提升模型性能。
怎么做到?就是下面这一部分:
2. 非极大值抑制(Non-Maximum Suppression,NMS)
2.1 多个重叠预测框现象
在上一篇对 YOLO 算法的基础介绍中,我们提到过,算法会将输入图像划分为网格,每个网格独立预测本网格内的目标,而我们在标注样本的标签时,会把目标归入目标中心点所在网格中。
就像这样:
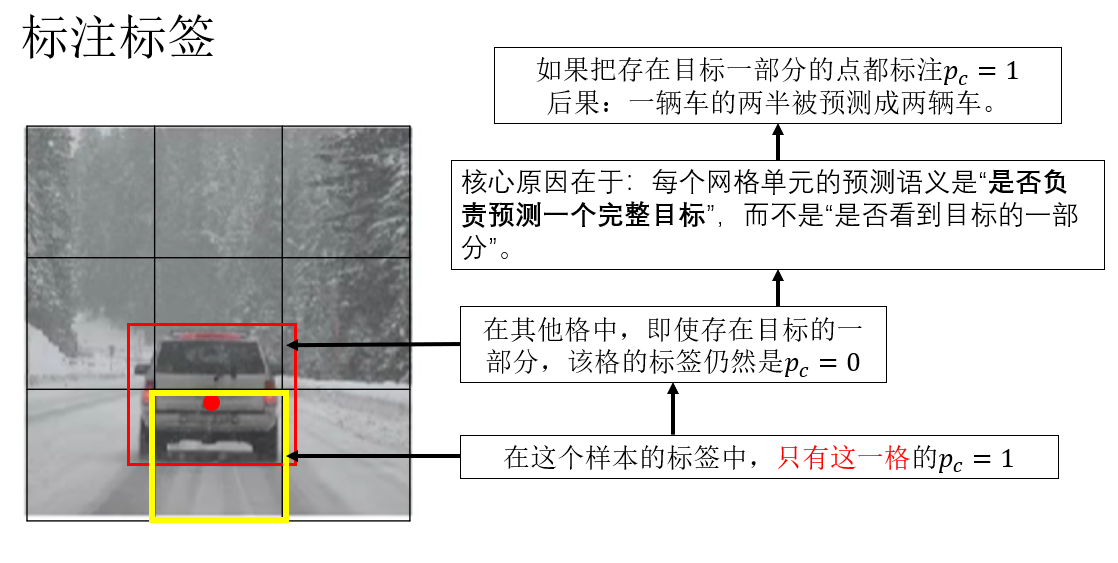
但是,这只是我们标注的逻辑 。
在推理阶段,模型并不知道"哪个网格被分配了哪个目标",它只是在每个网格上独立判断"这里是否存在目标",并回归一个可能的边界框。
因此,当网格内存在目标特征时,它就可能给出一个较高置信度的预测。
所以就会出现这样一种现象:模型明明已经"找对了目标",却给出了很多个高度重叠的预测框。
就像这样:
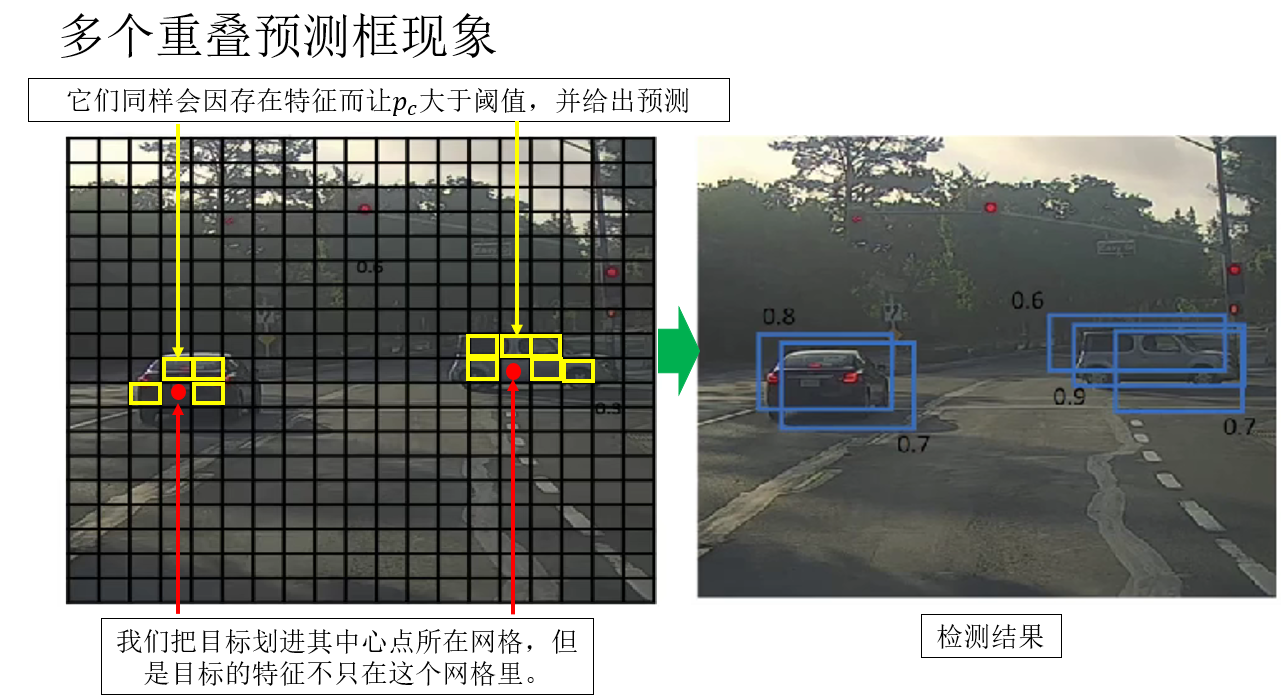
如果我们直接把这些结果全部输出,会发生什么?
答案是:一个目标被检测成了很多个目标 。
显然,这并不是我们想要的结果。
所以,就有了非极大值抑制,来看看如何使用它。
2.2 应用非极大值抑制
非极大值抑制的作用,就是在这些高度重叠的"候选框"中,只保留最有代表性的那一个,其余的全部抑制掉。
这里的"高度重叠",就是通过我们刚刚介绍的 IoU 来量化的。
我们来看一下非极大值抑制的标准流程:
- 按置信度排序 :将所有预测框按照分类得分从高到低排序。
- 选出当前得分最高的框,作为最终结果之一 :这个框被认为是对某个目标的"最可信描述"。
- 计算该框与其他所有框的 IoU :如果某个框与当前框的 IoU 大于预设阈值(如 0.5),说明它们指向的是同一个目标。
- 抑制(删除)这些高 IoU 的框 :只保留与当前框重叠程度较低的预测框。
- 重复上述过程,直到没有候选框为止。
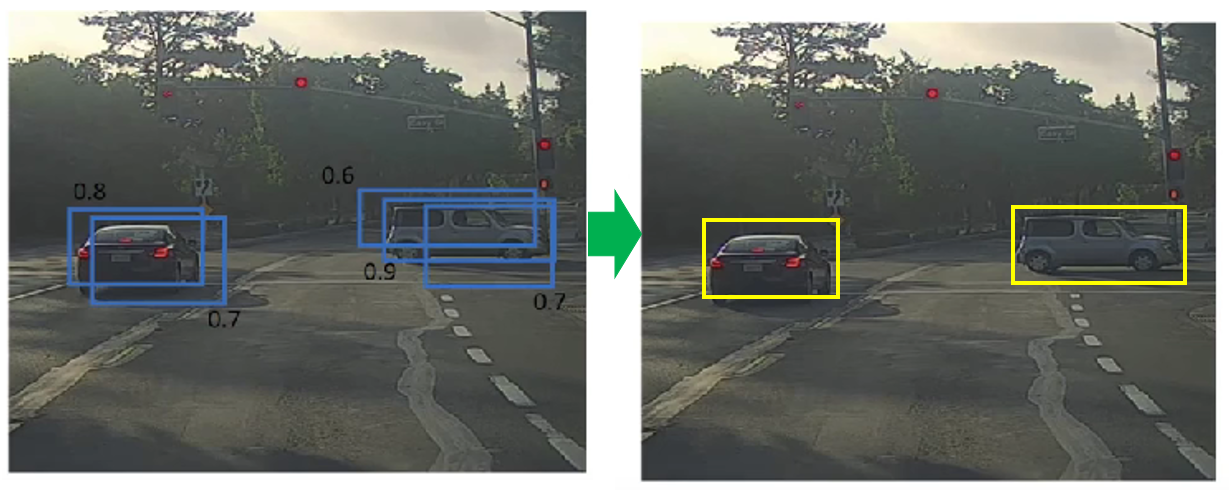
再演示一下,来看课程里这个例子:
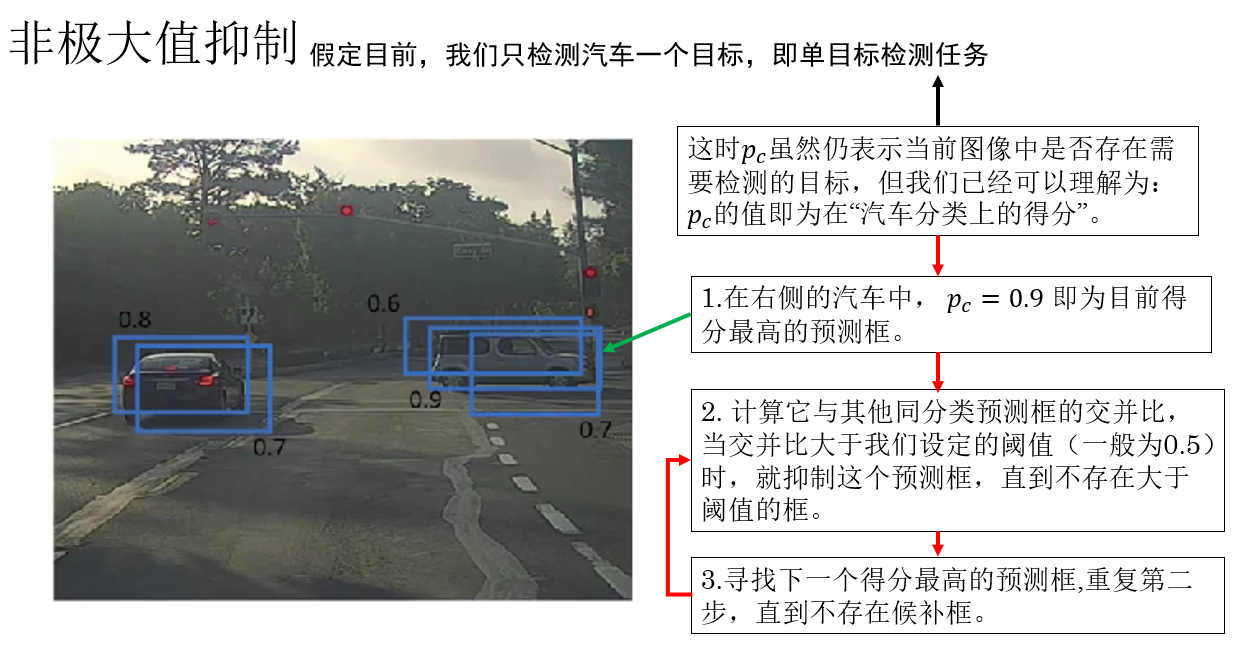
于是,应用非极大值抑制后,我们就得到了: 数量合理、位置准确、重复度极低的检测结果。
2.3 预测框在传播中的两次筛选
在应用了非极大值抑制后,你就会发现,我们在对目标的预测过程中,为了得到更准确的结果,进行了两次筛选。
(1)第一次筛选:基于置信度的"是否存在目标"
在模型完成正向传播后,每一个网格都会给出一组预测,其中首先便是目标存在概率 \(p_c\)
这一步中,通常会先进行一次置信度阈值过滤 :当 \(p_c\) 较低时,说明模型认为这里更可能是背景,这些预测框会被直接丢弃 。
只有 \(p_c\) 高于阈值的预测,才会进入下一阶段。
这一步的作用是:快速过滤掉大量明显的背景区域,减少后续计算量。
(2)第二次筛选:基于 IoU 的非极大值抑制
经过第一次筛选后,剩下的预测框已经基本都是:置信度较高且确实"命中目标特征"的候选框
现在要解决的问题就是:它们可能仍然在描述同一个目标。
于是,就需要第二次筛选------非极大值抑制 ,即通过 IoU 进行比较,只保留最具代表性的预测框,其余全部抑制掉。
这样,我们最终才能得到一组:数量合理、位置准确、对应真实目标的检测结果。

打个比方来理解:
第一次筛选是在问:"你确定你看到了东西吗?"
第二次筛选是在问:"你们是不是都在看同一个东西?"
2.4 多个检测目标:类别得分
我们现在已经知道了如何对单目标检测任务进行非极大值抑制,可要是扩展到多分类呢?
这时,你会发现,我们不能再用 \(p_c\) 的大小来代表检测目标的得分了。
因此,我们针对多目标检测任务中选择置信度最高的检测框引入了一个新概念:类别得分 。
它的公式并不难:
\[\text{Class Score}_n = p_c \times c_n \]
我们直接通过一个例子来说明它:
假设我们正在做一个 三分类目标检测任务 ,需要检测: 人(Person)、车(Car)、狗(Dog)
对于某一个预测框,模型给出了如下输出:
\[p_c = 0.8 \]
表示: 该位置存在某个目标的置信度为 0.8。
同时,模型在"存在目标"的前提下,给出了类别预测概率:
\[(c_{\text{person}}, c_{\text{car}}, c_{\text{dog}}) = (0.1, 0.7, 0.2) \]
在多类别目标检测中,真正用于排序和筛选预测框的不是 \(p_c\),而是分类得分,代入上面的数值,我们得到:
- 人(Person): \(0.8 \times 0.1 = 0.08\)
- 车(Car): \(0.8 \times 0.7 = 0.56\)
- 狗(Dog): \(0.8 \times 0.2 = 0.16\)
该预测框最终会被判定为:"车" ,它在"车"这一类别下的得分为:0.56
因此,在执行非极大值抑制时:该框会参与"车"类别的非极大值抑制 ,并与其他"车"类预测框按照 0.56 的得分进行排序和抑制。
总结一下:在多类别目标检测中,\(p_c\) 只负责判断"是否存在目标",真正用于筛选、排序和执行 NMS 的,是结合了类别信息的"分类得分"。
3. 锚框(Anchor Boxes)
3.1 为什么需要锚框?
在前面的内容中,我们默认了一个前提: 每个网格只预测一个边界框。
这种设定在"目标数量较少、尺度差异不大"的场景下是可以工作的,但它很快就会暴露出一个致命问题: 一个网格里,可能同时存在多个不同目标。
如果同一个网格中:
- 既有一个高而瘦的人。
- 又有一辆矮而宽的车 。

这时,如果我们仍然强制这个网格只预测一个边界框,那么显然,很可能二者都无法被较好地定位。
这不是训练不充分的问题, 而是面对多目标检测,输出空间本身不够用 。
锚框的引入,本质上就是为了解决多目标检测中,同一网格中出现多个不同形态的目标而导致的定位混乱现象。
3.2 如何使用锚框?
锚框的思想可以用一句话概括:不再让模型"从零开始"去猜边界框,而是让它在多个"预设形态"的参考框基础上进行微调。
具体做法是:在每一个网格位置预先放置 \(K\) 个形状不同的参考框 ,这些参考框就是锚框 。
例如:我们预先知道预测目标一个是人,一个是汽车,于是便预先为每个网格设置两个锚框:
- 一个偏高偏瘦,用来预测行人位置。
- 一个偏矮偏宽,用来预测汽车位置。
就像课程里这样:
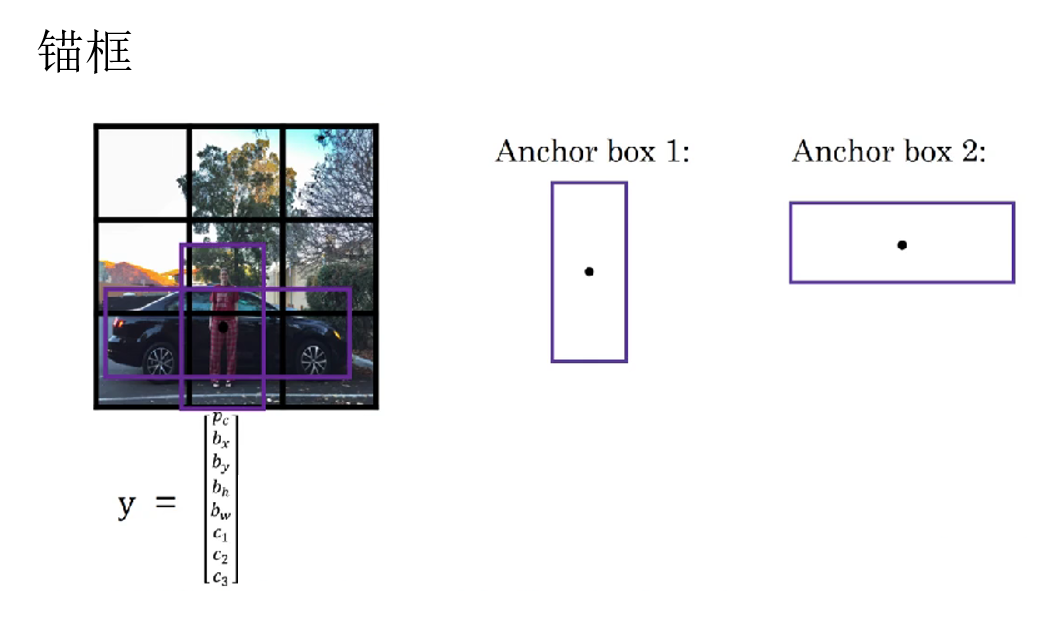
于是,一个网格不再只输出一组预测 ,而是输出 \(K\) 组预测结果 ,分别对应这 \(K\) 个锚框。
3.3 当同一个网格中可能出现多个目标时的标签变化
我们知道,在之前,我们假定一个网格中只会出现一种目标,因此,我们这样定义标签:
\[y =(p_c, b_x,b_y,b_h,b_w,c_1, c_2, \dots, c_n) \]
但很显然,当一个网格中可能出现多个目标时,一组标签是不够用的。如果网格里同时出现了行人和汽车,我们就要为它们各自设置一组标签来让网络学习。
同理,当一个网格不再只输出一组预测 ,而是输出 \(K\) 组预测结果 时,我们就要为其设置 \(K\) 组标签:
\[y =K \times(p_c, b_x,b_y,b_h,b_w,c_1, c_2, \dots, c_n) \]
就像这样:
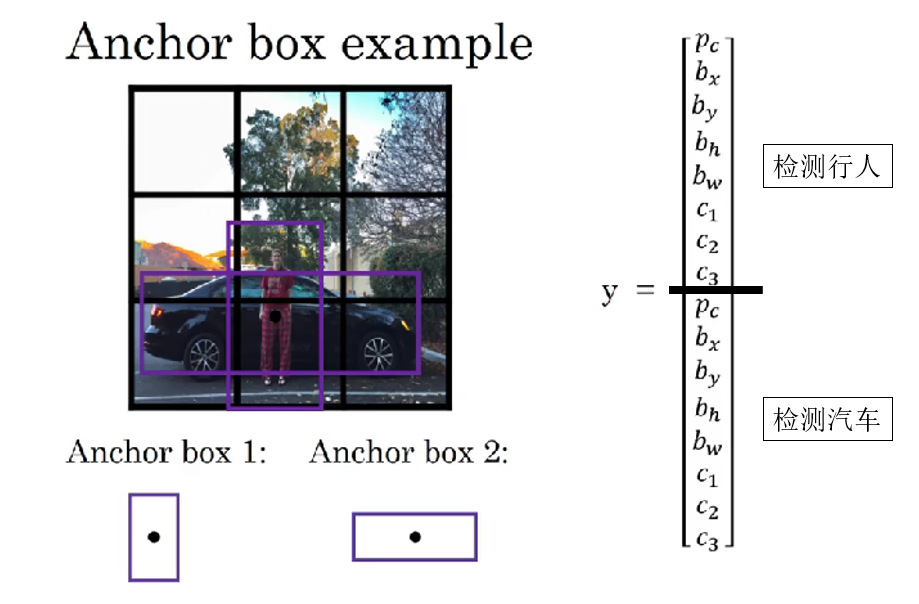
现在,我想你可能会有一个问题:我通过更改标签适应了同一网格中存在多种目标的情况,那网络不是就可以直接学每个目标的检测了吗?锚框是不是不设置也没有问题?
别急,我们了解完锚框的具体使用逻辑,这个问题自然会迎刃而解。
3.4 标签如何使用锚框
首先,在多锚框机制下,每个网格不仅有 \(K\) 个预测框,还对应 \(K\) 组标签。这些标签并不是随意分配的,而是与锚框紧密对应,形成训练的监督信号:
- 对于每个网格内的每个锚框,计算它与所有真实目标框的 IoU。
- 将 IoU 最大的目标分配给该锚框,该锚框就是正样本锚框。
- 如果某个锚框与任何目标 IoU 都低于阈值,则该锚框为负样本 ,其标签 \(p_c=0\),其他参数忽略。
这样,我们就完成了锚框和要检测的目标的匹配。
同时,锚框机制还把位置信息的学习转换为锚框中心和大小的微调 。也就是说,网络不再直接去预测目标在图像中的绝对位置和尺寸,而是预测目标相对于锚框的偏移量和缩放比例。
它并不是改变标签里的位置信息的语义,而是通过运算将原本的绝对尺度转换为相对锚框的偏移量并学习。
我们这里不摆复杂的公式,了解原理即可。
这部分其实和残差学习的逻辑有一定的相似之处:只需预测相对于参考框的微调量,降低了学习难度,使网络更容易收敛并稳定检测多目标。
现在,我们再来解释上面的问题:
你会发现 : 锚框其实是我们人为帮助模型进行目标检测的一种手工设计。
如果你只是简单地在标签中为同一网格增加多组目标信息,而不使用锚框,就会遇到这样几个问题:
- 没有锚框的目标匹配,输出与标签会匹配混乱。
- 没有锚框的偏移学习,面对多目标任务会收敛困难。
- 没有锚框的"个性定制",网络多目标检测的能力不足。
3.5 小结
这部分内容较多,我们简单小结一下:
锚框的引入是为了解决单网格只能预测一个目标而无法处理同网格多目标的问题 ,通过在每个网格预设多个不同形状的参考框,让网络只需预测目标相对于锚框的偏移量和类别概率 ,从而简化学习任务并提高收敛性。
每个网格对应 \(K\) 个锚框,也就对应 \(K\) 组标签,通过与真实目标的 IoU 匹配确定正负样本 。
如果没有锚框,网络在多目标检测中容易出现目标匹配混乱、偏移量学习困难和收敛不稳定等问题。
锚框本质上是一种人为设计的参考机制,用来帮助网络更高效、稳定地完成多目标检测。
4. 总结
| 概念 | 原理 | 比喻 |
|---|---|---|
| 交并比(IoU) | 衡量预测框与真实框重叠程度,计算公式为交集面积除以并集面积,越大表示预测越准确 | 就像量尺量两个重叠物体的重合面积,越大说明测量越精确 |
| 非极大值抑制(NMS) | 对候选预测框进行筛选,先按置信度排序,保留最可信预测框,再根据 IoU 删除重叠度高的框 | 第一次筛选:问"你确定看到东西了吗?",第二次筛选:问"你们是不是都在看同一个东西?" |
| 置信度(\(p_c\)) | 预测该网格存在目标的概率 | 判断"这里有没有东西" |
| 类别得分(Class Score) | 用 \(p_c \times c_n\) 表示某类别的最终得分,用于多类别 NMS 排序 | 确定目标的"身份得分",选择最可能的类别进行抑制 |
| 锚框(Anchor Boxes) | 在每个网格预设多个不同形状的参考框,让网络只需预测相对于锚框的偏移量和类别概率,每个锚框与真实目标通过 IoU 匹配形成正负样本 | 就像给网络提供模板,让它只需微调而不是从零猜测,类似残差学习只学变化量 |
| 标签变化 | 每个网格输出 \(K\) 组预测,对应 \(K\) 组标签,分别匹配不同锚框 | 原本一个网格只需写一份作业,现在每个模板都写一份作业 |
| 锚框作用 | 解决单网格多目标、提高收敛性、稳定训练 | 给网络参考框,让它"照模板微调"而不是盲目猜测 |