Transformer位置编码演进：从绝对位置到RoPE的数学本质

文章目录

Transformer位置编码演进：从绝对位置到RoPE的数学本质
- 引言：当Transformer"忘记"了顺序
- [一、绝对位置编码：为序列中的每个位置分配独特标识](#一、绝对位置编码：为序列中的每个位置分配独特标识)
- - [1.1 原始Transformer的正余弦编码](#1.1 原始Transformer的正余弦编码)
  - [1.2 可学习的位置编码](#1.2 可学习的位置编码)
- [二、相对位置编码：关注相对距离而非绝对位置](#二、相对位置编码：关注相对距离而非绝对位置)
- - [2.1 相对位置的核心思想](#2.1 相对位置的核心思想)
  - [2.2 T5的相对位置偏置](#2.2 T5的相对位置偏置)
- [三、 RoPE（旋转位置编码）的数学本质](#三、 RoPE（旋转位置编码）的数学本质)
- - [3.1 从复数旋转到高维空间](#3.1 从复数旋转到高维空间)
  - [3.2 RoPE的完整实现](#3.2 RoPE的完整实现)
  - [3.3 RoPE的数学本质：保持内积的相对性](#3.3 RoPE的数学本质：保持内积的相对性)
- [四、不同位置编码方案的比较与演进](#四、不同位置编码方案的比较与演进)
- - [4.1 各方案特性对比](#4.1 各方案特性对比)
  - [4.2 位置编码的演进趋势](#4.2 位置编码的演进趋势)
- [五、 RoPE在主流大模型中的应用与优化](#五、 RoPE在主流大模型中的应用与优化)
- - [5.1 LLaMA中的RoPE实现](#5.1 LLaMA中的RoPE实现)
  - [5.2 长度外推：NTK-aware Scaled RoPE](#5.2 长度外推：NTK-aware Scaled RoPE)
- [六、位置编码的未来发展方向](#六、位置编码的未来发展方向)
- - [6.1 动态位置编码](#6.1 动态位置编码)
  - [6.2 超长序列的位置编码](#6.2 超长序列的位置编码)
  - [6.3 多模态位置编码](#6.3 多模态位置编码)
- [七、实践建议：如何选择位置编码方案](#七、实践建议：如何选择位置编码方案)
- - [7.1 根据任务特性选择](#7.1 根据任务特性选择)
  - [7.2 根据资源约束选择](#7.2 根据资源约束选择)
  - [7.3 实现考虑](#7.3 实现考虑)
- 结论

Transformer位置编码演进：从绝对位置到RoPE的数学本质

引言：当Transformer"忘记"了顺序

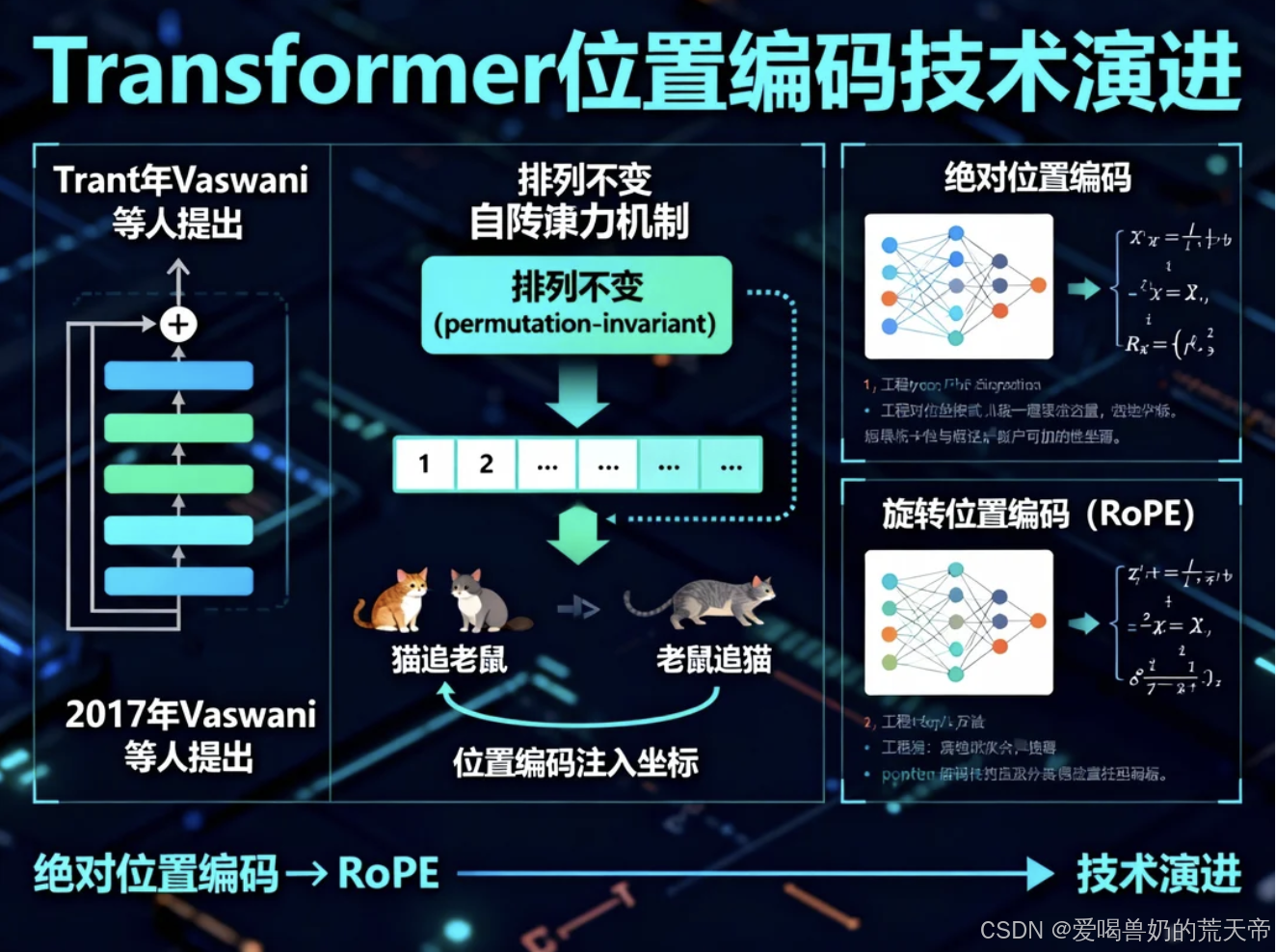
在深度学习处理序列数据的历程中，有一个根本性的突破发生在2017年：Vaswani等人提出了Transformer架构。这个架构彻底改变了自然语言处理的格局，但它有一个看似微小的技术细节------位置编码（Positional Encoding） 。为什么这个细节如此重要？因为Transformer的核心自注意力机制本身是排列不变（permutation-invariant） 的，它"看待"输入的序列就像我们看待一袋单词：知道有哪些单词，但不知道它们的顺序。

想象一下，如果语言模型无法区分"猫追老鼠"和"老鼠追猫"，那么所有基于序列的逻辑都将崩溃。位置编码就是解决这一问题的钥匙，它为每个单词的位置注入"坐标"，让模型能够理解序列中的顺序关系。本文将从最简单的绝对位置编码出发，一直深入到当前大模型广泛采用的旋转位置编码（RoPE），揭示这一技术演进背后的数学本质与工程智慧。

一、绝对位置编码：为序列中的每个位置分配独特标识

1.1 原始Transformer的正余弦编码

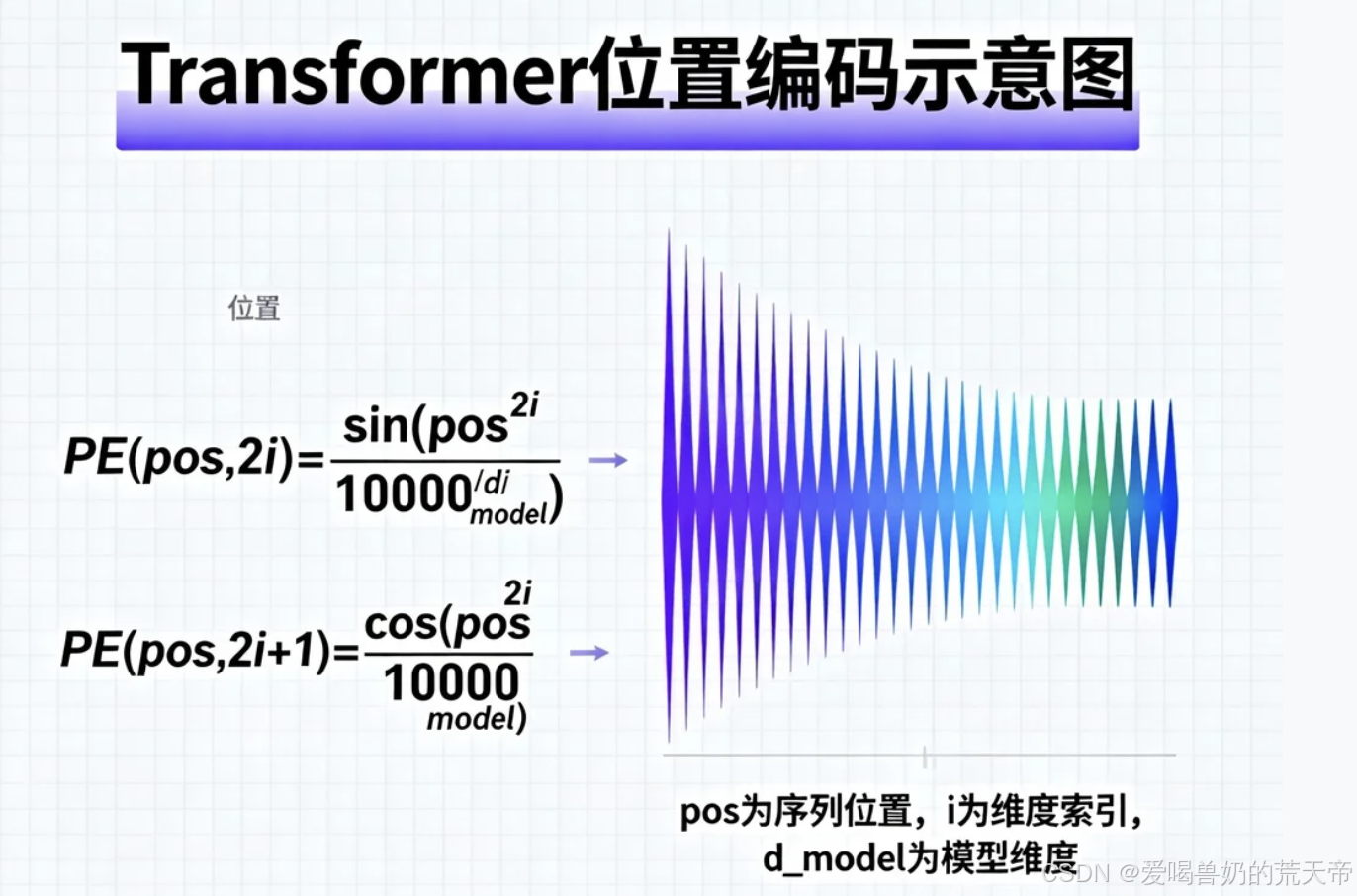
原始Transformer论文中的位置编码设计堪称经典，它采用了一组固定的正余弦函数来生成位置向量：

python 复制代码

import torch
import math

def get_original_transformer_pe(max_len, d_model):
    """
    生成原始Transformer的位置编码矩阵
    max_len: 最大序列长度
    d_model: 模型维度
    """
    pe = torch.zeros(max_len, d_model)
    
    for pos in range(max_len):
        for i in range(0, d_model, 2):
            # 偶数维度使用正弦
            pe[pos, i] = math.sin(pos / (10000 ** (2 * i / d_model)))
            # 奇数维度使用余弦
            if i + 1 < d_model:
                pe[pos, i + 1] = math.cos(pos / (10000 ** (2 * i / d_model)))
    
    return pe

# 示例：可视化位置编码
import matplotlib.pyplot as plt

pe = get_original_transformer_pe(100, 512)
plt.figure(figsize=(12, 6))
plt.imshow(pe[:50, :100].T, aspect='auto', cmap='RdBu')
plt.colorbar()
plt.xlabel('位置索引')
plt.ylabel('编码维度')
plt.title('原始Transformer位置编码（前50位置，前100维度）')
plt.show()

这个设计的巧妙之处在于几个方面：

确定性函数：编码是确定性的，不需要学习参数
值域有界：正弦余弦函数的值域在[-1, 1]之间，与词嵌入的范围相似
相对位置的可学习性：模型可以学习关注相对位置而非绝对位置

但这种编码方式有一个潜在问题：它假设模型在处理序列时预先知道最大长度，这在处理可变长序列或需要泛化到训练时未见过的长度时可能成为限制。

1.2 可学习的位置编码

BERT等后续模型采用了更简单直接的方法：可学习的位置嵌入。每个位置学习一个独立的向量：

python 复制代码

class LearnablePositionalEncoding(nn.Module):
    """可学习的位置编码"""
    def __init__(self, max_len, d_model):
        super().__init__()
        self.pe = nn.Parameter(torch.randn(max_len, d_model))
        
    def forward(self, x):
        # x: [batch_size, seq_len, d_model]
        seq_len = x.size(1)
        return x + self.pe[:seq_len, :]

这种方法简单有效，但存在两个主要限制：

模型无法处理比训练时更长的序列
每个位置独立学习，可能无法很好捕捉位置之间的相对关系

二、相对位置编码：关注相对距离而非绝对位置

2.1 相对位置的核心思想

随着研究的深入，研究者发现对于许多语言任务，单词之间的相对位置比绝对位置更重要。例如，在语法分析中，"动词"和"它的宾语"之间的关系比它们各自在句子中的绝对位置更重要。

相对位置编码的核心思想是：在计算注意力时，显式地考虑查询和键之间的相对距离。2018年，Shaw等人首次在Transformer中引入了相对位置编码：

python 复制代码

class RelativePositionEncoding(nn.Module):
    """简化的相对位置编码实现"""
    def __init__(self, max_relative_distance, d_model):
        super().__init__()
        self.max_relative_distance = max_relative_distance
        # 为每个可能的相对距离学习一个嵌入
        self.embeddings = nn.Embedding(2 * max_relative_distance + 1, d_model)
        
    def forward(self, seq_len):
        # 生成相对位置索引
        range_vec = torch.arange(seq_len)
        distance_mat = range_vec[None, :] - range_vec[:, None]
        
        # 将距离限制在[-max_relative_distance, max_relative_distance]内
        distance_mat_clipped = torch.clamp(
            distance_mat, 
            -self.max_relative_distance, 
            self.max_relative_distance
        )
        
        # 转换为非负索引
        final_mat = distance_mat_clipped + self.max_relative_distance
        
        return self.embeddings(final_mat)

2.2 T5的相对位置偏置

T5模型采用了一种更高效的相对位置编码变体：相对位置偏置。它不是将位置信息添加到词嵌入中，而是直接添加到注意力分数中：

python 复制代码

def compute_relative_position_bias(seq_len, num_heads, max_distance=128):
    """
    计算相对位置偏置
    简化实现，实际T5使用学习到的偏置参数
    """
    # 创建相对距离矩阵
    relative_indices = torch.arange(seq_len).unsqueeze(0) - torch.arange(seq_len).unsqueeze(1)
    relative_indices = torch.clamp(relative_indices, -max_distance, max_distance)
    
    # 为每个注意力头学习不同的偏置
    bias = nn.Parameter(torch.randn(num_heads, 2 * max_distance + 1))
    
    # 为每个位置对获取对应的偏置
    relative_bias = bias[:, relative_indices + max_distance]
    
    return relative_bias

# 在注意力计算中应用相对位置偏置
def attention_with_relative_bias(q, k, v, relative_bias):
    """带相对位置偏置的注意力计算"""
    attn_scores = torch.matmul(q, k.transpose(-2, -1)) / math.sqrt(q.size(-1))
    attn_scores = attn_scores + relative_bias  # 添加相对位置偏置
    attn_weights = F.softmax(attn_scores, dim=-1)
    return torch.matmul(attn_weights, v)

这种方法显著减少了参数量，并且能够处理比训练时更长的序列，只要相对距离在训练范围内。

三、 RoPE（旋转位置编码）的数学本质

3.1 从复数旋转到高维空间

旋转位置编码（RoPE）由苏剑林等人提出，其核心思想非常优雅：通过旋转操作将位置信息编码到词向量中。要理解RoPE，我们先从二维空间中的复数旋转开始。

在二维复数平面上，一个复数可以表示为 ( z = x + yi )。当我们将其旋转角度θ时，新坐标为：
z ′ = z ⋅ e i θ = ( x + y i ) ( cos ⁡ θ + i sin ⁡ θ ) z' = z \cdot e^{i\theta} = (x + yi)(\cos\theta + i\sin\theta) z′=z⋅eiθ=(x+yi)(cosθ+isinθ)

在RoPE中，我们将这个思想扩展到高维空间。假设我们有一个d维的词向量，我们将它看作d/2个二维向量组成的集合。对于每个二维子空间，我们应用一个旋转，旋转角度与位置成正比。

python 复制代码

def apply_rope_2d(x, position):
    """
    在二维空间中应用旋转位置编码
    x: [batch_size, seq_len, 2] 或 [batch_size, seq_len, d_model] 的最后两维
    position: 位置索引
    """
    # 计算旋转角度：与位置成正比
    theta = position * 0.0001  # 这里使用简化的小常数，实际为10000^{-2i/d}
    
    # 旋转矩阵
    cos_theta = math.cos(theta)
    sin_theta = math.sin(theta)
    
    # 应用旋转
    x1, x2 = x[..., 0], x[..., 1]
    x1_rot = x1 * cos_theta - x2 * sin_theta
    x2_rot = x1 * sin_theta + x2 * cos_theta
    
    return torch.stack([x1_rot, x2_rot], dim=-1)

3.2 RoPE的完整实现

在实际实现中，RoPE被同时应用于查询（Q）和键（K）向量，这样在计算注意力分数时，相对位置信息会自动体现在内积中：

python 复制代码

def apply_rope(x, positions, theta_base=10000.0):
    """
    应用旋转位置编码到高维向量
    x: [batch_size, seq_len, num_heads, head_dim]
    positions: [seq_len] 位置索引
    """
    batch_size, seq_len, num_heads, head_dim = x.shape
    
    # 将head_dim分成d/2对
    half_dim = head_dim // 2
    freq_seq = torch.arange(half_dim, device=x.device).float()
    
    # 计算频率：theta_i = theta_base^{-2i/d}
    freqs = 1.0 / (theta_base ** (freq_seq / half_dim))
    
    # 为每个位置计算角度
    positions = positions.unsqueeze(-1)  # [seq_len, 1]
    angles = positions * freqs.unsqueeze(0)  # [seq_len, half_dim]
    
    # 计算正弦和余弦
    cos_vals = torch.cos(angles).unsqueeze(0).unsqueeze(2)  # [1, seq_len, 1, half_dim]
    sin_vals = torch.sin(angles).unsqueeze(0).unsqueeze(2)  # [1, seq_len, 1, half_dim]
    
    # 重塑x为两个部分以便旋转
    x_reshaped = x.reshape(batch_size, seq_len, num_heads, half_dim, 2)
    x1, x2 = x_reshaped[..., 0], x_reshaped[..., 1]
    
    # 应用旋转
    x1_rot = x1 * cos_vals - x2 * sin_vals
    x2_rot = x1 * sin_vals + x2 * cos_vals
    
    # 重新组合
    x_rotated = torch.stack([x1_rot, x2_rot], dim=-1)
    x_rotated = x_rotated.reshape(batch_size, seq_len, num_heads, head_dim)
    
    return x_rotated

3.3 RoPE的数学本质：保持内积的相对性

RoPE最精妙的地方在于它的数学性质。当我们将RoPE同时应用于查询向量q和键向量k时，它们的内积变为：

⟨ RoPE ( q , m ) , RoPE ( k , n ) ⟩ = ⟨ q , k ⟩ ⋅ cos ⁡ ( ( m − n ) θ ) + 交叉项 \langle \text{RoPE}(q, m), \text{RoPE}(k, n) \rangle = \langle q, k \rangle \cdot \cos((m-n)\theta) + \text{交叉项} ⟨RoPE(q,m),RoPE(k,n)⟩=⟨q,k⟩⋅cos((m−n)θ)+交叉项

这个公式表明，注意力分数仅依赖于q和k的原始内容以及它们之间的相对位置(m-n)，而不是它们的绝对位置m和n。这正是我们想要的特性！

python 复制代码

def rope_attention(q, k, v, positions):
    """使用RoPE的注意力计算"""
    # 应用RoPE到q和k
    q_rope = apply_rope(q, positions)
    k_rope = apply_rope(k, positions)
    
    # 计算注意力分数
    attn_scores = torch.matmul(q_rope, k_rope.transpose(-2, -1)) / math.sqrt(q.size(-1))
    attn_weights = F.softmax(attn_scores, dim=-1)
    
    return torch.matmul(attn_weights, v)

四、不同位置编码方案的比较与演进

4.1 各方案特性对比

编码类型	代表模型	核心思想	优点	缺点
绝对位置编码	原始Transformer	为正弦余弦函数分配固定位置	简单，可泛化到未见过的长度	假设固定最大长度，不能很好捕捉相对位置
可学习绝对编码	BERT, GPT-2	每个位置学习一个独立向量	灵活，可从数据中学习	无法处理比训练更长的序列，参数量大
相对位置编码	Transformer-XL, T5	编码相对距离而非绝对位置	更好的相对位置建模，长度外推性好	实现相对复杂，计算开销较大
旋转位置编码	GPT-NeoX, LLaMA	通过旋转操作编码位置信息	精确的相对位置编码，长度外推性好，数学性质优雅	实现相对复杂，需要特定优化

4.2 位置编码的演进趋势

从绝对位置到相对位置再到旋转位置，位置编码的演进呈现出几个明显趋势：

从绝对到相对：越来越强调相对位置关系的重要性
从加法到乘法：从将位置信息加到词嵌入中，变为通过变换（如旋转）融入
从启发式到理论驱动：从启发式的正弦函数到有严格数学基础的旋转操作
长度外推能力的增强：现代位置编码越来越关注处理比训练时更长的序列

五、 RoPE在主流大模型中的应用与优化

5.1 LLaMA中的RoPE实现

Meta的LLaMA系列模型采用了RoPE，并在实现上进行了优化：

python 复制代码

class LlamaRoPE(nn.Module):
    """LLaMA中的RoPE实现，进行了优化"""
    def __init__(self, dim, max_seq_len=2048, theta=10000.0):
        super().__init__()
        self.dim = dim
        self.theta = theta
        
        # 预计算频率和旋转矩阵
        inv_freq = 1.0 / (theta ** (torch.arange(0, dim, 2).float() / dim))
        t = torch.arange(max_seq_len).float()
        freqs = torch.einsum('i,j->ij', t, inv_freq)
        
        # 预计算旋转矩阵
        self.register_buffer('cos_cached', torch.cos(freqs))
        self.register_buffer('sin_cached', torch.sin(freqs))
        
    def forward(self, x, positions):
        seq_len = positions.shape[-1]
        cos = self.cos_cached[:seq_len]
        sin = self.sin_cached[:seq_len]
        
        # 应用旋转的高效实现
        x1 = x[..., 0::2]  # 偶数索引
        x2 = x[..., 1::2]  # 奇数索引
        
        # 旋转操作
        rotated_x1 = x1 * cos - x2 * sin
        rotated_x2 = x1 * sin + x2 * cos
        
        # 重新组合
        result = torch.zeros_like(x)
        result[..., 0::2] = rotated_x1
        result[..., 1::2] = rotated_x2
        
        return result

5.2 长度外推：NTK-aware Scaled RoPE

原始RoPE在处理远长于训练序列的文本时仍会遇到困难。研究者提出了NTK-aware Scaled RoPE来改进长度外推能力：

python 复制代码

def ntk_scaled_rope(x, positions, dim, base=10000, scale_factor=2.0):
    """
    NTK-aware Scaled RoPE
    通过调整频率基来增强长度外推能力
    """
    # 调整频率基
    adjusted_base = base * scale_factor ** (dim / (dim - 2))
    
    # 应用调整后的RoPE
    return apply_rope(x, positions, theta_base=adjusted_base)

这种方法的核心思想是：当序列长度增加时，适当"拉伸"频率基，使得高频部分变化更慢，从而让模型能够更好地泛化到更长的序列。

六、位置编码的未来发展方向

6.1 动态位置编码

当前的位置编码大多是静态的，但序列中的位置重要性可能是动态变化的。未来的方向可能包括：

内容感知的位置编码：位置编码不仅取决于位置，还取决于该位置的内容
可学习的位置编码方案：让模型自己学习如何编码位置信息
层次化位置编码：同时编码字符级、词级、句子级等多层次的位置信息

6.2 超长序列的位置编码

随着模型处理序列长度的不断增加（从最初的512到现在的100K+），如何有效编码超长序列中的位置信息成为关键挑战：

压缩位置表示：使用更紧凑的方式表示长序列中的位置
局部与全局结合：结合局部相对位置和全局绝对位置
层次化相对位置：在多个粒度上编码相对位置关系

6.3 多模态位置编码

在处理多模态数据（如图像、视频、音频）时，位置编码需要适应不同模态的特性：

二维位置编码：为图像处理设计二维网格位置编码
时空位置编码：为视频同时编码空间和时间位置
跨模态对齐的位置编码：在不同模态间对齐位置信息

七、实践建议：如何选择位置编码方案

7.1 根据任务特性选择

短文本分类任务：简单的绝对位置编码可能就足够了
长文档处理：相对位置编码或RoPE更合适
代码生成/数学推理：需要精确位置信息的任务适合RoPE
多语言模型：需要考虑不同语言语序差异，相对位置编码可能更有优势

7.2 根据资源约束选择

计算资源有限：简单的绝对位置编码计算开销最小
内存受限：RoPE相比可学习的绝对位置编码参数量更少
需要部署到不同长度：相对位置编码或RoPE的长度外推性更好

7.3 实现考虑

python 复制代码

def create_position_encoding(config, model_type):
    """根据配置选择位置编码方案"""
    if config.position_encoding == "absolute":
        return AbsolutePositionEncoding(config.max_seq_len, config.hidden_size)
    elif config.position_encoding == "learnable":
        return LearnablePositionalEncoding(config.max_seq_len, config.hidden_size)
    elif config.position_encoding == "relative":
        return RelativePositionEncoding(config.max_relative_distance, config.hidden_size)
    elif config.position_encoding == "rope":
        return RoPEEncoding(config.hidden_size, config.max_seq_len)
    else:
        raise ValueError(f"未知的位置编码类型: {config.position_encoding}")

结论

位置编码从Transformer的一个看似微小的技术细节，已经发展成为影响模型性能的关键因素。从绝对位置编码到相对位置编码，再到当前主流的旋转位置编码（RoPE），这一演进过程反映了我们对序列建模理解的不断深化。

RoPE以其优雅的数学形式和优秀的长度外推能力，已经成为当前大语言模型的标准配置。它的核心洞察------通过旋转操作将相对位置信息编码到注意力机制中------不仅解决了位置编码的根本问题，还为未来的研究提供了新的思路。

然而，位置编码的故事远未结束。随着模型处理更长的序列、更复杂的多模态数据，以及更动态的任务需求，我们可能需要更灵活、更智能的位置编码方案。理解位置编码的演进历程和数学本质，将帮助我们更好地设计下一代序列模型。

在人工智能理解语言的旅程中，位置编码就像是给无界的语言空间添加的坐标系。它让模型能够在这个空间中定位、导航，最终理解语言的内在结构和意义。这一技术仍在快速发展中，而每一次进步都在推动着语言模型向更智能、更理解人类语言的方向迈进。

Transformer位置编码演进：从绝对位置到RoPE的数学本质

文章目录