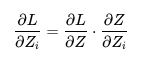在GPT Model中,初始化了Transformer模型头尾、MTP多token预测模块以及中间所需的Embedding和Rotary Embedding。在那之后,传入transformer的decoder,正式进行Attention以及MLP的层层叠叠计算。非常朴实无华。

这里可以通过传入自定义的Spec来定制你想要的模型结构。默认情况下就是最常见的transformer decoder结构。pre_process和post_process用于判断当前rank上的模型是不是pipeline开始或者结束的部分。
具体的模型定义是core/transformer/transformer_block/TransformerBlock,其中会进行_build_layers来创建具体的模型参数。对于layers,根据layer specs来一层层创建torch.nn.ModuleList格式的层。先知道当前PP开始的这一层,确定每一层在完整的模型里是第几层;然后获取这一层的具体spec,最后调用build_module。如果是最后一层,还需要加上最后的layernorm。
CPU Offloading是transformer engine提供的把一部分模型层权重或激活搬到CPU、异步预取来隐藏传输开销和降低显存占用的能力
以最常见的GPT模型为例,首先会有get_gpt_decoder_block_spec生成TransformerBlockSubmodules,其中 layer_specs 是若干个 ModuleSpec(module=TransformerLayer, submodules=TransformerLayerSubmodules(...)),子模块规格里包含输入 LN、SelfAttention、BiasDropoutAdd、(可选) CrossAttention、MLP 等;layer_norm 指定块尾的 LayerNorm 实现。另外layer_spec.module是类TransformerLayer,因此build_module返回的是实例化的TransformerLayer,此时就是调用了transformerlayer的init。这些会被放进ModuleList。
每个TransformerLayer的组成在core/transformer/transformer_layer/TransformerLayer中。在init里,可以看到以下几个内容:
- input LayerNorm,对输入数据做层归一化。在transformer中相当于对每个token的embedding维度做归一化,在保证输入内容不过大过小的同时维持其分布特点。现在的主流是pre-norm,即归一化在注意力/MLP之前,先LN再输入后续计算后连接残差,y=x+sublayer(LN(x)),保障稳定的梯度流稳定训练;原始的post-norm即先计算子层,再连接残差后统一LN,由于稳定性等问题基本不再使用。y=LN(x+sublayer(x))。在Megatron中,进注意力前先input layernorm,再进入mlp之前做pre_mlp_layernorm。final layernorm是在全局计算最后做一次post norm,可选
- self_attention,attention bias dropout(把加bias和dropout和残差连接都包含起来的高效实现,另外现在一般dropout都设置成0.0),可选post norm,cross attention(一般也用不到),pre_mlp_layernorm(一个新的pre-norm)
- MLP Block,包含FFN层。FFN其实就是MLP,这里还会额外记录一下层数,以及合并残差dropout等的BiasDropout
- 选择性重计算 selective recompute。0.12.1版本没有MoE的重计算,可能是涉及到专家重放或者说MoE激活也不是很大;具体来说就是不再保留这些计算起来很快但是中间激活值非常大的内容,而是用checkpoint without output上下文包裹LN和MLP算子,丢弃输出只保留输入。在反向到这里的时候,重新根据保存的输入计算得到中间的激活,从而用计算换显存。众所周知现在的硬件显存比算力吃紧的多(大小,带宽)。
IdentityOp等其实就是空壳,什么都不做,只返回输入。相当于nn.Module的一个占位用
在初始化好这些以后,GPT Model会初始化一个output layer,这个地方会有些不同。在transformers这个库里,或者直接使用torch实现的版本里,这里就是用nn.Linear线性层输出即可。但是为了支持模型并行,需要用ColumnPrallelLinear特殊的Linear实现。ColumnParallel代表着Y = XA + b中的A第二维并行化,即列并行A = [A_1, ..., A_p].每个TP rank计算自己的那个Yi = X*Ai,通过all-gather操作收集所有分片。
- Init初始化自己的TP位置,计算输出维度output_size//world size,因为只能输出给定数量的列的内容。存储分割后维度,input维度的权重。因为linear执行的是X*A^T。最后初始化权重
- 前向传播forward里,输入seq,bs,hidden。会考虑是否将输入复制到各个rank上(例如开启SP或者异步梯度计算就不需要复制,同步发生在别的地方)。
copy_to_tensor_model_parallel_region前向值返回输入,反向时会对梯度all reduce保障TP内GPU有相同输入梯度
- 实际的矩阵乘法是linear_with_grad_accumulation_and_async_allreduce,如果有sp就先all gather从buffer里读输入;然后用torch.matmul(total_input, weight.t()),最后加bias。最后也会有判断是否要gather output。前向all gather,反向则split切分
- 正向和反向基本是共轭的。Backward过程中我们需要计算:输入x的梯度,权重w的梯度,偏置b的梯度。权重梯度可以延迟计算,把多个micro batch的权重梯度计算合并减少矩阵乘法调用的次数。公式:y=x*W+b
- 准备完整的输入,如果采用SP,则异步all gather所有输入x。此时我们是可以计算x的梯度的,因为用不上x本身,x梯度计算公式如下。gy是上游梯度的切片。如果要用完整的梯度,则需要通过all reduce把所有梯度分片计算结果求和。
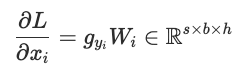
- 前一步异步all gather完成后,可以计算权重梯度了。prepare input tensors把张量内存连续,并且把seq,bs,hidden重构为二维矩阵 seq*bs, hidden用于大规模GEMM计算(提速和避免复制开销)
- 这里异步进行输入x的梯度的all reduce求和,从而能够与后续权重梯度计算重叠(计算权重w梯度不需要x的梯度)。如果使用了SP,则使用reduce scatter聚合后的输入梯度分片给其他参与SP的GPU。权重梯度计算公式如下。
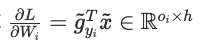
- 计算权重梯度完成后,计算偏置梯度(最简单,直接求和上游梯度,因为W和X都求导没了)
- 最后等待所有发起的异步通信完成后,返回grad_input(x梯度),grad_weight(权重w梯度),以及grad_bias(偏置梯度)
上述反向传播的核心优化就是重叠通信计算。体现在两个地方:1、序列并行在最开始要all gather x,此步骤与计算x的梯度重合,一直到需要计算权重梯度之前都不会被阻塞;2、all reduce或者reduce scatter x的梯度,此时输入梯度已经计算完成不会再用在反向传播的其他地方,因此可以与权重梯度重合。
那么列并行结束了。行并行RowParallelLinear有用在哪里呢?可以看到GPT的MLP中包含两个linear_fc,第一个是列并行,第二个是行并行。在get get layer local spec中以及mlp的module spec,可以看到有一些RowParallelLinear出现。



Row中,权重沿着第一维输入维度切分(匹配输入的hidden),输入沿着最后一维切分(hidden)。计算出来的结果z=x*w^T = (s,b,h//tp) * (h//tp, o) = s,b,o。也就是说结果的维度就是完整的维度,但是每个数都只是一部分,必须求和获取完整的结果。
前向时,Row的输入x如果已经是切片,则无需处理;如果不是,必须要scatter 切分。输出时,必须要all reduce(reduce scatter如果是SP)从而把局部结果求和成完整输出。公式是Z_i = X_i * W_i^T, Z=AllReduce(Z_i),Y=Z+b
反向时,从上游获取的是完整梯度g_Y(代码中为grad_output)。计算b的梯度,sum_{s,b} g_Y即可(相当于对每个token都产生梯度求和);接下来,由于前向传播中的All Reduce操作Z=sum(Z)的Jacobian矩阵(partial Z/ partial Z_i)为单位对角阵I,因此对每个GPU来说所需的梯度就是完整的梯度g_Y(所以All Reduce操作的反向就是复制梯度到各个GPU)
根据链式法则来计算。要计算左侧对每个GPU的梯度,则右侧为上游g_Y乘一个雅可比矩阵。Z的第 k个元素只依赖于 Zi 的第 k个元素且偏导数为 1(当索引相同时),其他为 0,所以雅可比矩阵是对角线为 1 的单位矩阵

线性层就比较简单了。求权重梯度的公式和之前是一样的,如下。total input即X_i,用grad_output.t()和total input做matmul即可(g_Y^T X_i)。此处得到的形状就是out*h//tp,和分片的权重矩阵是一样的
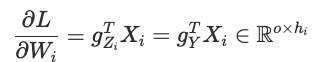
最后计算输入X的梯度。直接g_Y*W_i即可,得到的就是沿着hidden分片的输入形状。当然这里就不需要all reduce梯度了,形状已经对了。
如果有SP,则使用all gather(reduce scatter的反向操作)把完整的x拼起来还回去。
一次前向 all‑reduce + 一次反向 all‑gather。与 ColumnParallelLinear 形成对称:
- Column:前向 all‑gather(可选) + 反向 all‑reduce。
- Row:前向 all‑reduce + 反向 all‑gather(可选)。
经常可以看见,这两个是配套使用的。为什么呢?

一个原因是,Column的输出结果是分片的,直接传给Row能避免掉一次gather减少通信量,只需要在最后Row输出时来一次all-reduce。如果用两个column连接起来,中间必须有一次all gather,最后还要一次all reduce,大幅增加了通信量;
第二个原因是,Colomn和Row层中每个GPU计算的量分别是(sb*h) * (h o_i)和(sbo_i) * (o_i *o)。当h和o大小相当时,计算量是接近的,能够实现负载均衡。
part 1中有提到,每一个矩阵乘法,MK*KN需要的浮点计算次数是2MNK(MN个元素,每个元素需要K次乘法和加法)
另外,需要扩大维度的时候,输入x比输出小(h->o),可以用输入完整X输出部分O即Column;缩减则反过来用Row。在MLP中很多时候h升维到4h再降回来h,刚好配对使用。