排序算法：基数排序算法

文章目录

- 一、基数排序是什么？
- 二、图示解析
- [三、时间 & 空间复杂度分析](#三、时间 & 空间复杂度分析)
- 四、基数排序完整示例

一、基数排序是什么？

基数排序是一种"不比较大小"的排序算法，它按"数位"一位一位地排。这是它和冒泡 / 快排 / 归并排序本质上最大的区别。

基数排序的核心思想

以十进制整数为例：

先按个位排序

再按十位排序

再按百位排序

......

直到最高位；每一轮都是稳定排序

二、图示解析

假设数组：

cpp 复制代码

[170, 45, 75, 90, 802, 24, 2, 66]

按「个位」排序

cpp 复制代码

桶0: 170, 90
桶2: 802, 2
桶4: 24
桶5: 45, 75
桶6: 66

收集后：

cpp 复制代码

[170, 90, 802, 2, 24, 45, 75, 66]

按「十位」排序

cpp 复制代码

桶0: 802, 2
桶2: 24
桶4: 45
桶6: 66
桶7: 170, 75
桶9: 90

结果：

cpp 复制代码

[802, 2, 24, 45, 66, 170, 75, 90]

按「百位」排序

cpp 复制代码

桶0: 2, 24, 45, 66, 75, 90
桶1: 170
桶8: 802

总的来说，排序如下所示：

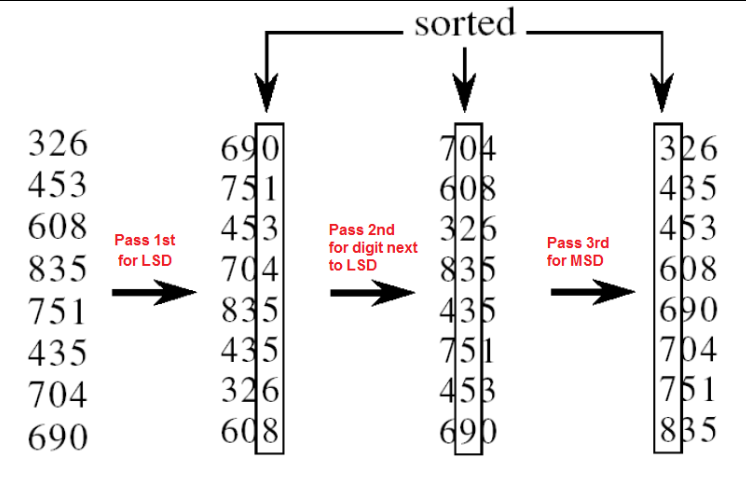
为什么"必须是稳定排序"？

如果低位排序打乱了高位的相对顺序；结果一定错

因此：

基数排序 = 多轮稳定排序

通常使用：计数排序、桶排序作为"子排序"

基数排序的优缺点

优点：

不比较大小

时间复杂度稳定

大数据量时非常快

特别适合：整数、固定长度字符串、ID / 编号

缺点：

只能用于 "可拆分为位"的数据

需要额外空间

不适合：浮点数、比较规则复杂的对象

三、时间 & 空间复杂度分析

设：

n = 元素个数

d = 最大数字的位数

k = 基数（十进制 = 10）

时间复杂度：

cpp 复制代码

O(d × (n + k)) ≈ O(d × n)

线性时间排序（非常快）

空间复杂度：

cpp 复制代码

O(n + k)

四、基数排序完整示例

示例：对非负整数排序

cpp 复制代码

#include <iostream>
#include <vector>
using namespace std;

// 按某一位进行计数排序
void countingSort(vector<int>& arr, int exp)
{
    int n = arr.size();
    vector<int> output(n);
    int count[10] = {0};

    // 统计当前位出现次数
    for (int i = 0; i < n; i++)
        count[(arr[i] / exp) % 10]++;

    // 前缀和（确定位置）
    for (int i = 1; i < 10; i++)
        count[i] += count[i - 1];

    // 从后往前保证稳定性
    for (int i = n - 1; i >= 0; i--)
    {
        int digit = (arr[i] / exp) % 10;
        output[count[digit] - 1] = arr[i];
        count[digit]--;
    }

    arr = output;
}

// 基数排序
void radixSort(vector<int>& arr)
{
    int maxVal = *max_element(arr.begin(), arr.end());

    for (int exp = 1; maxVal / exp > 0; exp *= 10)
        countingSort(arr, exp);
}

int main()
{
    vector<int> arr = {170, 45, 75, 90, 802, 24, 2, 66};

    radixSort(arr);

    for (int x : arr)
        cout << x << " ";
}