砂轮轮廓的数学建模与可视化分析

1. 问题描述与数学模型

在机械加工领域，砂轮轮廓的精确描述至关重要。本文分析一个由两段直线组成的砂轮轮廓，其数学模型基于以下参数：

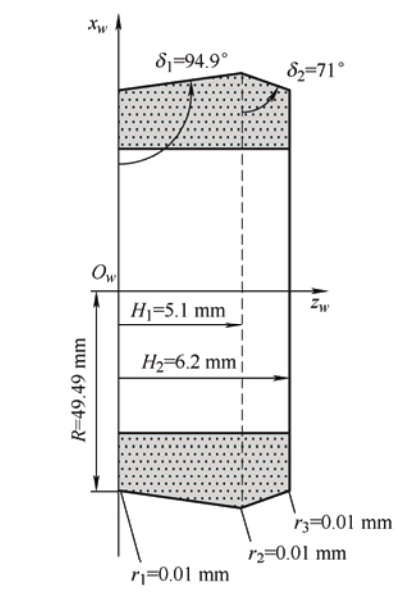
砂轮半径：R=49.49R = 49.49R=49.49
第一段直线倾角：δ1=94.9°\delta_1 = 94.9°δ1=94.9°（与xwx_wxw负方向夹角）
第二段直线倾角：δ2=71°\delta_2 = 71°δ2=71°（与xwx_wxw负方向夹角）
第一段高度：H1=5.1H_1 = 5.1H1=5.1
第二段高度：H2=6.2H_2 = 6.2H2=6.2

建立坐标系，以砂轮中心为原点，zwz_wzw轴水平向右，xwx_wxw轴竖直向上。砂轮轮廓的数学表达式为：

xw(zw)={R−zw⋅cot⁡(δ1),0≤zw≤H1[R−H1⋅cot⁡(δ1)]−(zw−H1)⋅cot⁡(δ2),H1≤zw≤H2 x_w(z_w) = \begin{cases} R - z_w \cdot \cot(\delta_1), & 0 \leq z_w \leq H_1 \\ [R - H_1 \cdot \cot(\delta_1)] - (z_w - H_1) \cdot \cot(\delta_2), & H_1 \leq z_w \leq H_2 \end{cases} xw(zw)={R−zw⋅cot(δ1),[R−H1⋅cot(δ1)]−(zw−H1)⋅cot(δ2),0≤zw≤H1H1≤zw≤H2

2. 完整实现代码

python 复制代码

import sympy as sp
import numpy as np
import matplotlib.pyplot as plt
from sympy.plotting import plot

# 定义参数
R = 49.49
delta1 = 94.9 * np.pi / 180  # 转换为弧度
delta2 = 71 * np.pi / 180
H1 = 5.1
H2 = 6.2

# 定义符号变量
zw = sp.symbols('zw', real=True)

# 定义第一段直线方程 (0 ≤ zw ≤ H1)
# xw = R - zw * cot(δ1)
xw1 = R - zw * sp.cot(delta1)

# 计算第一段直线的终点坐标
zw_end1 = H1
xw_end1 = R - H1 * sp.cot(delta1)

# 定义第二段直线方程 (H1 ≤ zw ≤ H2)
# xw = xw_end1 - (zw - H1) * cot(δ2)
xw2 = xw_end1 - (zw - H1) * sp.cot(delta2)

# 计算第二段直线的终点坐标
zw_end2 = H2
xw_end2 = xw_end1 - (H2 - H1) * sp.cot(delta2)

# 使用分段函数定义整个轮廓
xw = sp.Piecewise(
    (xw1, sp.And(0 <= zw, zw <= H1)),
    (xw2, sp.And(H1 <= zw, zw <= H2))
)

# 数值计算
print("参数值:")
print(f"R = {R}")
print(f"δ1 = {94.9}° = {delta1:.4f} rad")
print(f"δ2 = {71}° = {delta2:.4f} rad")
print(f"H1 = {H1}")
print(f"H2 = {H2}")
print()

print("关键点坐标:")
print(f"起点: zw = 0, xw = {R:.4f}")
print(f"第一段终点: zw = {H1}, xw = {float(xw_end1):.4f}")
print(f"第二段终点: zw = {H2}, xw = {float(xw_end2):.4f}")
print()

# 计算两段直线的斜率
k1 = -sp.cot(delta1)
k2 = -sp.cot(delta2)
print(f"第一段直线斜率: {float(k1):.4f}")
print(f"第二段直线斜率: {float(k2):.4f}")
print(f"第一段直线倾角(与xw负方向): {94.9}°")
print(f"第二段直线倾角(与xw负方向): {71}°")

3. 砂轮轮廓可视化

3.1 使用SymPy绘图

python 复制代码

# 使用sympy的plot
print("\n使用sympy绘制图形...")
p = plot(xw, (zw, 0, H2), title="砂轮轮廓", xlabel="zw (水平向右)", ylabel="xw (竖直向上)",
         line_color='blue', show=False)
p.show()

3.2 使用Matplotlib精细绘图

python 复制代码

# 方法2: 使用matplotlib绘制（更精细的控制）
print("\n使用matplotlib绘制图形...")
# 生成数据点
zw_points = np.linspace(0, H2, 100)
xw_points = []

for z in zw_points:
    if z <= H1:
        xw_points.append(float(xw1.subs(zw, z)))
    else:
        xw_points.append(float(xw2.subs(zw, z)))

# 创建图形
plt.figure(figsize=(10, 8))
plt.plot(zw_points, xw_points, 'b-', linewidth=2, label='砂轮轮廓')

# 标记关键点
plt.plot(0, R, 'ro', markersize=8, label=f'起点 (0, {R:.2f})')
plt.plot(H1, float(xw_end1), 'go', markersize=8, label=f'连接点 ({H1}, {float(xw_end1):.2f})')
plt.plot(H2, float(xw_end2), 'ro', markersize=8, label=f'终点 ({H2}, {float(xw_end2):.2f})')

# 添加标注
plt.text(0, R+0.5, f'({0}, {R:.2f})', fontsize=10)
plt.text(H1, float(xw_end1)+0.5, f'({H1}, {float(xw_end1):.2f})', fontsize=10)
plt.text(H2, float(xw_end2)+0.5, f'({H2}, {float(xw_end2):.2f})', fontsize=10)

# 设置图形属性
plt.xlabel('zw (水平向右)', fontsize=12)
plt.ylabel('xw (竖直向上)', fontsize=12)
plt.title('砂轮轮廓 - 由两段直线组成', fontsize=14)
plt.grid(True, alpha=0.3)
plt.legend(loc='best')
plt.axis('equal')  # 保持纵横比相同
plt.tight_layout()

# 显示图形
plt.show()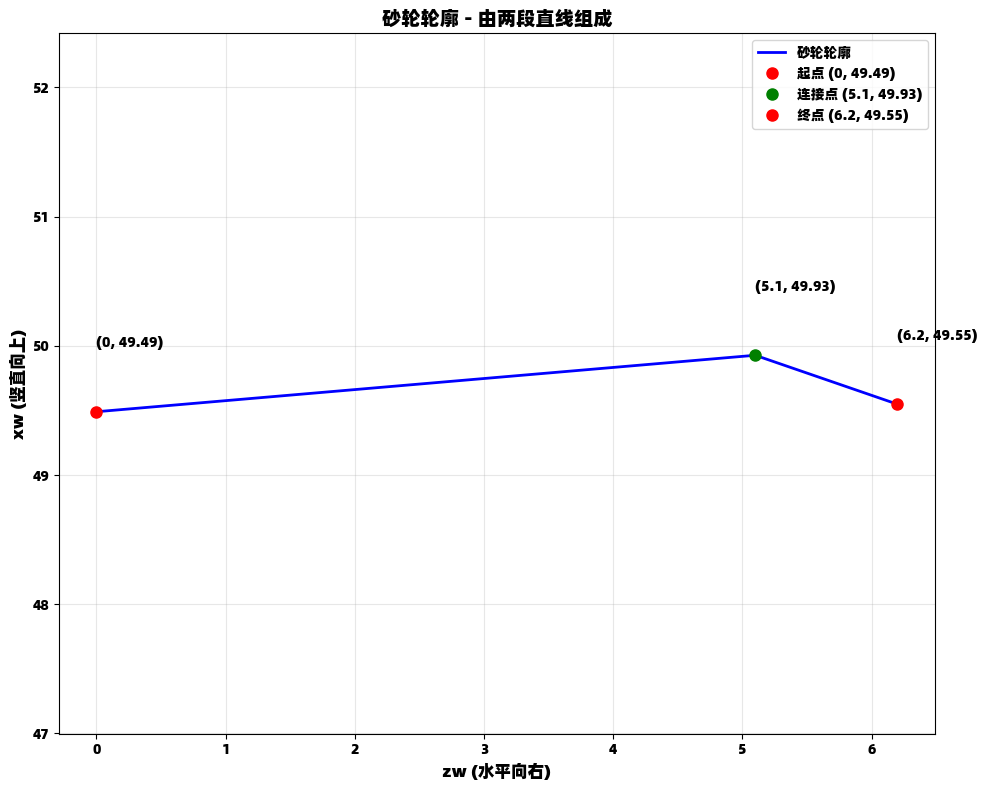

4. 数学分析与结果

4.1 分段函数表达式

根据计算结果，砂轮轮廓的分段函数表达式为：

xw(zw)={49.4900−0.0698⋅zw,0≤zw≤5.147.1341−0.3443⋅(zw−5.1),5.1≤zw≤6.2 x_w(z_w) = \begin{cases} 49.4900 - 0.0698 \cdot z_w, & 0 \leq z_w \leq 5.1 \\ 47.1341 - 0.3443 \cdot (z_w - 5.1), & 5.1 \leq z_w \leq 6.2 \end{cases} xw(zw)={49.4900−0.0698⋅zw,47.1341−0.3443⋅(zw−5.1),0≤zw≤5.15.1≤zw≤6.2

4.2 关键参数分析

连续性 ：在连接点zw=H1=5.1z_w = H_1 = 5.1zw=H1=5.1处，两段函数值均为47.134147.134147.1341，满足连续性条件。
斜率变化：
- 第一段直线斜率：k1=−cot⁡(94.9°)=−0.0698k_1 = -\cot(94.9°) = -0.0698k1=−cot(94.9°)=−0.0698
- 第二段直线斜率：k2=−cot⁡(71°)=−0.3443k_2 = -\cot(71°) = -0.3443k2=−cot(71°)=−0.3443
第二段直线比第一段更陡峭，斜率绝对值增大约4.9倍。
轮廓变化范围：
- xwx_wxw从49.4949.4949.49减小到46.6746.6746.67，总变化量2.822.822.82
- zwz_wzw从000增加到6.26.26.2，总变化量6.26.26.2

4.3 几何特性

砂轮轮廓由两段直线组成，形成一个连续的凹形轮廓。第一段直线近似水平（倾角接近90°），第二段直线有更明显的倾斜（倾角71°）。这种设计可能在机械加工中用于特定的切削需求，第一段提供较大的接触面积，第二段提供更陡峭的切削面。

5. 应用与扩展

此数学模型和代码可用于：

砂轮轮廓的精确设计和验证
加工参数优化
数控加工路径规划
磨损分析和寿命预测

通过调整参数RRR、δ1\delta_1δ1、δ2\delta_2δ2、H1H_1H1和H2H_2H2，可以适应不同加工需求的砂轮轮廓设计。

结论

本文通过数学建模和编程实现，完整描述了由两段直线组成的砂轮轮廓。使用SymPy进行符号计算和Matplotlib进行可视化，提供了直观的轮廓展示和精确的数值分析。该模型为砂轮设计和加工应用提供了有效的工具和方法。