【C++数据结构进阶】从B + 树 / B * 树到数据库索引：B树的进化之路与 MySQL 实战解析

前言

在上一篇博客中，我们深入剖析了 B 树的设计精髓 ------ 通过 "多叉平衡" 结构降低树的高度，减少磁盘 IO 次数，完美解决了海量数据的外部存储检索问题。但在实际应用中，尤其是数据库、文件系统等场景，B 树却很少被直接使用，取而代之的是它的 "进化版"------B + 树和 B * 树。

你是否好奇：B 树已经如此高效，为什么还需要进一步优化？B + 树在 B 树的基础上做了哪些改进？今天，我们就来揭开这些谜底，带你打通从数据结构到数据库应用的任督二脉！下面就让我们正式开始吧！

一、B 树的 "软肋"：为什么需要 B + 树和 B * 树？

B 树的核心优势是 "低高度、平衡、磁盘友好"，但在实际应用中，它依然存在几个难以忽视的局限性，这些局限性成为了 B + 树和 B * 树诞生的契机。

1.1 范围查询效率低

B 树的关键字分散在各个节点中（根节点、分支节点、叶子节点都可能存储关键字），当需要进行范围查询时（比如 "查找所有大于 100 且小于 200 的关键字"），需要遍历整个树的多个分支，多次回溯，效率很低。

举个例子：在一棵 3 阶 B 树中查找 "50~150" 的关键字，需要先找到 50 所在的叶子节点，然后通过父节点指针回溯到分支节点，再向下遍历到 150 所在的叶子节点，整个过程涉及多次磁盘 IO，操作复杂。

1.2 关键字冗余存储

B 树的分支节点中存储了关键字，而这些关键字同样会出现在叶子节点中（或子树中），导致关键字的冗余存储。对于海量数据来说，这种冗余会占用大量的磁盘空间，增加存储成本。

1.3 磁盘 IO 利用率不高

B 树的每个节点同时存储关键字和子节点指针，且关键字的长度可能不固定（比如字符串类型），这会导致节点的大小难以精准匹配磁盘块大小。此外，分支节点中的关键字会占用部分空间，使得每个节点能存储的子节点指针数量减少，间接增加了树的高度，影响检索效率。

1.4 顺序访问不友好

B 树的叶子节点之间没有直接的关联，无法像链表一样进行高效的顺序访问。在需要遍历所有数据（比如全表扫描）时，只能从根节点开始逐层遍历，效率远低于链表式的顺序访问。

为了解决这些问题，B + 树应运而生。它在 B 树的基础上进行了针对性优化，完美适配了数据库、文件系统等场景的需求。而 B * 树则是 B + 树的进一步升级，在空间利用率上实现了更大的突破。

二、B + 树：为索引而生的 "进化版 B 树"

2.1 B + 树的定义与核心特性

B + 树是 B 树的变体，本质上是一棵平衡的多路搜索树，其设计初衷是为了优化索引的查询和存储效率。与 B 树相比，B + 树在结构上做了 4 点关键改进，形成了自己独有的特性：

核心特性 1：所有关键字都存储在叶子节点

B + 树的分支节点（根节点、非叶子节点）仅存储关键字和子节点指针，不存储数据记录；所有关键字及其对应的 data 都集中在叶子节点中，且叶子节点中的关键字按照从小到大的顺序排列。

这一设计解决了 B 树的关键字冗余问题 ------ 分支节点的关键字仅作为 "索引指引"，无需存储重复数据，大幅节省了磁盘空间。

核心特性 2：分支节点的子节点指针与关键字个数相同

B 树的分支节点中，子节点指针个数 = 关键字个数 + 1；而 B + 树的分支节点中，子节点指针个数 = 关键字个数。

具体来说，B + 树分支节点的结构为：(K₁, P₁, K₂, P₂, ..., Kₙ, Pₙ)，其中：

Kᵢ 为关键字，且K₁ < K₂ < ... < Kₙ；

Pᵢ 为子节点指针，指向的子树中所有关键字的取值范围是 [Kᵢ, Kᵢ₊₁)（对于最后一个指针 Pₙ，其指向的子树关键字 ≥ Kₙ）。

这种结构让分支节点的索引逻辑更清晰，每个指针对应的关键字范围更明确，查找时无需额外判断，效率更高。

核心特性 3：叶子节点通过链表串联

B + 树的所有叶子节点通过一个双向链表（或单向链表）连接起来，链表中的关键字保持有序。这一设计让范围查询和顺序访问变得极其高效：

范围查询：只需找到范围的起始关键字所在的叶子节点，然后通过链表依次遍历到范围的结束关键字，无需回溯父节点；

顺序访问：直接遍历叶子节点的链表即可，效率等同于链表的 O (N)，但无需逐层遍历树结构。

核心特性 4：查找必达叶子节点

B + 树的查找过程中，无论目标关键字是否存在，最终都必须到达叶子节点。分支节点的关键字仅用于指引查找方向，不会在分支节点中 "命中" 数据。

这一特性保证了查找效率的稳定性 ------ 所有查找操作的磁盘 IO 次数都等于树的高度，不会出现 B 树中 "在分支节点命中" 的不确定情况，便于系统优化。

2.2 B + 树的结构示意图

为了更直观地理解 B + 树的结构，我们以一棵 3 阶 B + 树为例，结构如下：

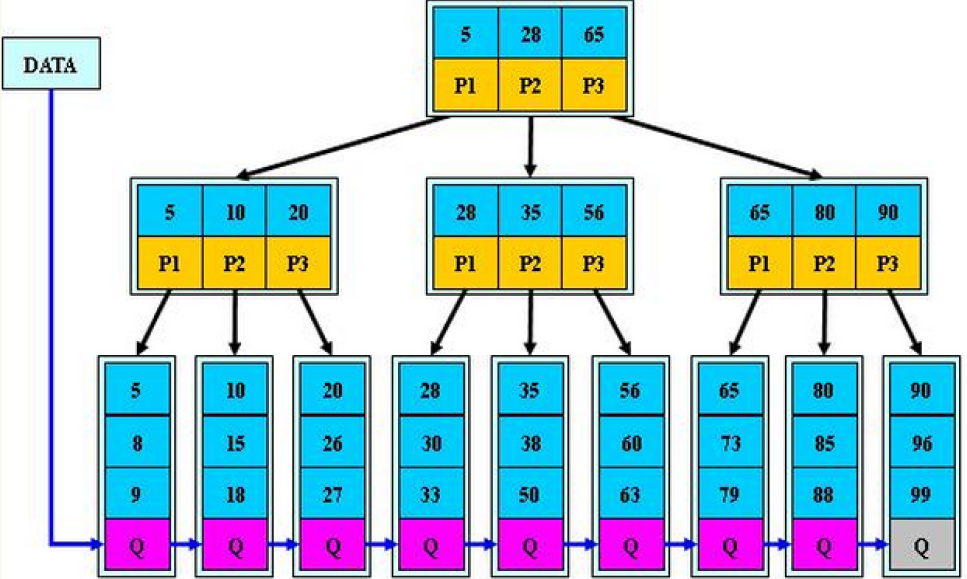结构解读：

根节点 [5, 28, 65]：三个关键字，三个子节点指针，分别指向子树 [5, 10, 20) 、 [28, 35, 56)和[65, 80, 90)；

分支节点 [5, 10, 20]：三个关键字，三个子节点指针，分别指向子树 [5, 8, 9) 、 [10, 15, 18)和[20, 26, 27)；

叶子节点 [5, 8, 9] 、 [10, 15, 18]和[20, 26, 27] 等：存储关键字和对应数据，通过链表串联，链表顺序为 5→8→9→10→15→18→......→99。

2.3 B + 树的查找、插入与分裂流程

（1）查找流程

B + 树的查找过程与 B 树类似，但最终必须到达叶子节点：

从根节点开始，根据目标关键字 key 与当前节点关键字的比较结果，选择对应的子节点指针，进入下一层节点；

重复步骤 1，直到进入叶子节点；

在叶子节点的有序关键字中查找 key：

若找到，返回对应的 data；

若未找到，返回 "不存在"。

（2）插入流程

B + 树的插入核心原则：插入位置始终在叶子节点，插入后需保证叶子节点有序、链表连接正常，且节点关键字个数不超过 m-1（m 为阶数）。若节点满，则进行分裂。

插入流程步骤：

查找插入位置：通过 B + 树的查找逻辑，找到 key 应插入的叶子节点（若 key 已存在，根据业务需求处理，如覆盖或报错）；

插入关键字：按照有序原则将 key 插入到叶子节点的对应位置，更新叶子节点的链表连接；

检测节点是否满：若叶子节点的关键字个数 ≤ m-1，插入成功；若等于 m，则需要分裂；

节点分裂 ：

将叶子节点的关键字平均分成两部分（前半部分留在原节点，后半部分移入新节点）；

新节点接入叶子节点的链表中（更新前后节点的链表指针）；

将分裂后的中间关键字（通常是新节点的第一个关键字）插入到父分支节点中；

若父节点也满，则重复分裂流程，直到根节点（根节点分裂后树的高度加 1）。

（3）分裂流程与 B 树的区别

B + 树的分裂与 B 树的核心差异在于：

B 树分裂时，中间关键字会从原节点移除，上升到父节点；

B + 树分裂时，中间关键字会保留在原节点（叶子节点），仅将其副本插入到父节点中，保证所有关键字都集中在叶子节点。

这一差异是由 B + 树 "所有关键字存储在叶子节点" 的特性决定的，确保了分裂后不会丢失关键字。

2.4 B + 树的优势总结

对比 B 树，B + 树的核心优势如下：

对比维度	B 树	B + 树
范围查询	效率低，需多次回溯	效率高，叶子节点链表遍历
顺序访问	需逐层遍历树结构	直接遍历叶子节点链表
存储效率	关键字冗余，存储成本高	分支节点仅存索引，节省空间
查找稳定性	可能在分支节点命中，IO 次数不确定	必达叶子节点，IO 次数固定
数据一致性	关键字分散，维护成本高	数据集中在叶子节点，维护简单

正是这些优势，让 B + 树成为了数据库索引的 "首选数据结构"。

三、B * 树：空间利用率拉满的 "终极进化版"

B * 树是 B + 树的进一步优化，核心目标是提高节点的空间利用率 ，减少分裂次数，降低磁盘 IO 开销。它在 B + 树的基础上增加了一个关键设计：非根、非叶子节点增加指向兄弟节点的指针。

3.1 B * 树的核心特性

核心特性 1：兄弟节点指针优化分裂逻辑

B * 树的非根、非叶子节点除了存储关键字和子节点指针，还额外存储一个兄弟节点指针（通常是右兄弟指针）。这一设计让节点满时，优先尝试 "借空间" 而非 "分裂"，大幅降低了分裂频率。

核心特性 2：分裂策略更高效

B + 树的节点满时，直接分裂为两个节点，各占一半数据；而 B * 树的分裂策略分为两步：

尝试向兄弟节点 "借空间"：若当前节点满，且其右兄弟节点未满，则将当前节点的部分关键字移到兄弟节点中，同时更新父节点中对应关键字的范围（因为兄弟节点的关键字范围发生了变化）；

兄弟节点也满时才分裂：若兄弟节点也满，则将当前节点和兄弟节点各拿出 1/3 的关键字，共同分裂出一个新节点，三个节点的关键字个数均为 2m/3 左右（m 为阶数）。

这种分裂策略有如下优势：

减少分裂次数：借空间操作无需创建新节点，比分裂更高效；

提高空间利用率 ：B + 树分裂后节点的空间利用率为 50%，而 B * 树分裂后节点的空间利用率约为 66.7%，大幅节省磁盘空间；

降低树的高度：空间利用率高意味着每个节点能存储更多关键字，树的高度更低，磁盘 IO 次数更少。

核心特性 3：继承 B + 树的所有优势

B * 树完全继承了 B + 树的核心优势：

所有关键字存储在叶子节点；

叶子节点通过链表串联，支持高效范围查询；

查找必达叶子节点，效率稳定。

3.2 B * 树的结构示意图

以 3 阶 B * 树为例，结构如下：

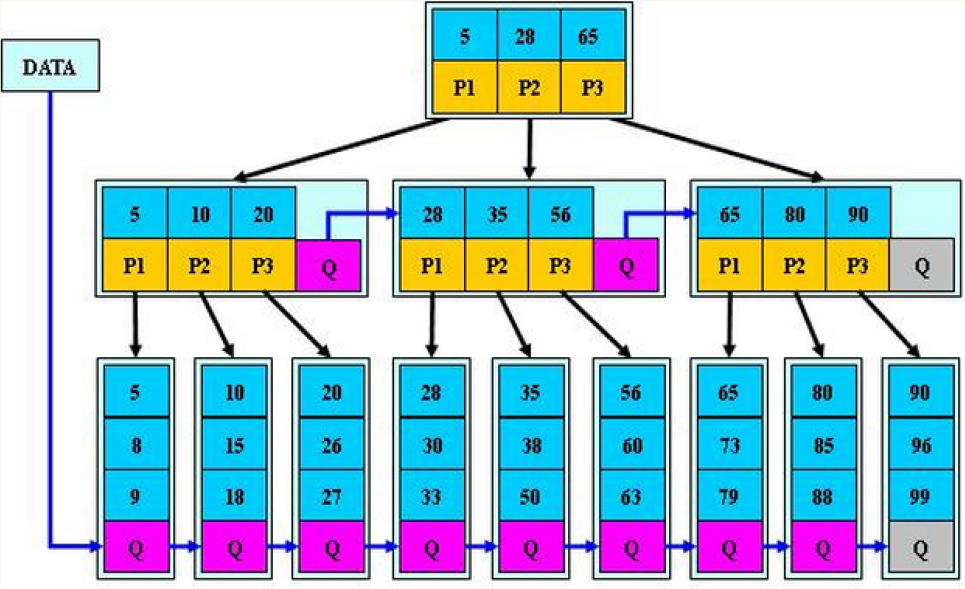
3.3 B * 树与 B + 树的对比

对比维度	B + 树	B * 树
节点结构	无兄弟指针	非根非叶子节点有兄弟指针
分裂策略	直接分裂为两个节点，各占 1/2	优先借空间，否则分裂为三个节点，各占 1/3
空间利用率	约 50%	约 66.7%
分裂频率	高	低
适用场景	读写均衡、范围查询频繁	写操作密集、空间资源紧张

B * 树的空间利用率更高，分裂次数更少，更适合写操作密集的场景（如高并发插入的数据库表）；而 B + 树的实现更简单，读写均衡性更好，是更通用的索引选择。

四、B 树家族大比拼：B 树 vs B + 树 vs B * 树

为了让大家更清晰地梳理三者的关系和差异，我们用一张表格总结核心对比：

特性	B 树	B + 树	B * 树
关键字存储位置	分支节点 + 叶子节点	仅叶子节点（分支节点存索引）	仅叶子节点（分支节点存索引）
子节点指针个数	关键字个数 + 1	关键字个数	关键字个数
叶子节点连接	无	双向链表	双向链表
查找终点	分支节点或叶子节点	必达叶子节点	必达叶子节点
范围查询效率	低	高	高
空间利用率	低（关键字冗余）	中（分裂后 50%）	高（分裂后 66.7%）
分裂频率	中	高	低
核心优势	基础平衡多叉树，实现简单	范围查询高效，读写均衡	空间利用率高，分裂少
典型应用	少量外部存储场景	数据库索引（MyISAM、InnoDB）、文件系统	高并发写场景、大容量数据存储

一句话总结就是：B 树是基础，B + 树优化了查询和存储，B * 树优化了空间和分裂 ------ 三者都是为了适应外部存储场景，核心目标是减少磁盘 IO，提高检索效率。

五、B 树家族的核心应用：MySQL 索引实战

B + 树（及变种）最核心的应用场景就是数据库索引。MySQL 作为最流行的开源关系型数据库，其两大核心存储引擎（MyISAM、InnoDB）都采用 B + 树作为索引结构，但实现方式存在显著差异。

5.1 索引的本质：为什么选择 B + 树？

MySQL 官方对索引的定义是：索引是帮助 MySQL 高效获取数据的数据结构 。简单来说，索引就是 "数据的目录"，其核心目标是减少数据查找时的磁盘 IO 次数。

选择 B + 树作为索引结构的核心原因：

低高度：B + 树是多路平衡树，高度通常在 2~4 层（对于 1 亿条数据，100 阶 B + 树的高度仅为 3 层），最多 3 次磁盘 IO 即可找到目标数据；

范围查询高效 ：叶子节点链表让范围查询（如 WHERE id BETWEEN 100 AND 200）无需回溯，效率远超其他结构；

顺序访问友好：全表扫描时直接遍历叶子节点链表，效率高于 B 树；

空间利用率高：分支节点仅存索引，不存数据，节省磁盘空间，能让每个节点存储更多关键字，进一步降低树高。

5.2 MyISAM 存储引擎的 B + 树索引实现（非聚集索引）

MyISAM 是 MySQL 5.5.8 版本之前的默认存储引擎，不支持事务、行锁，支持全文索引，其索引实现采用非聚集索引（又称 "二级索引"），核心特点是 "索引文件与数据文件分离"。

（1）索引结构

MyISAM 的索引文件（.MYI）和数据文件（.MYD）是两个独立的文件，索引结构如下：

主索引（Primary Key） ：B + 树结构，叶子节点的 data 域存储的是数据记录的物理地址（如磁盘块地址 0x07、0x56）；

辅助索引（Secondary Key）：与主索引结构完全一致，叶子节点的 data 域同样存储数据记录的物理地址，仅要求关键字可以重复（无需唯一）。

（2）主索引示意图

以Col1为主索引：

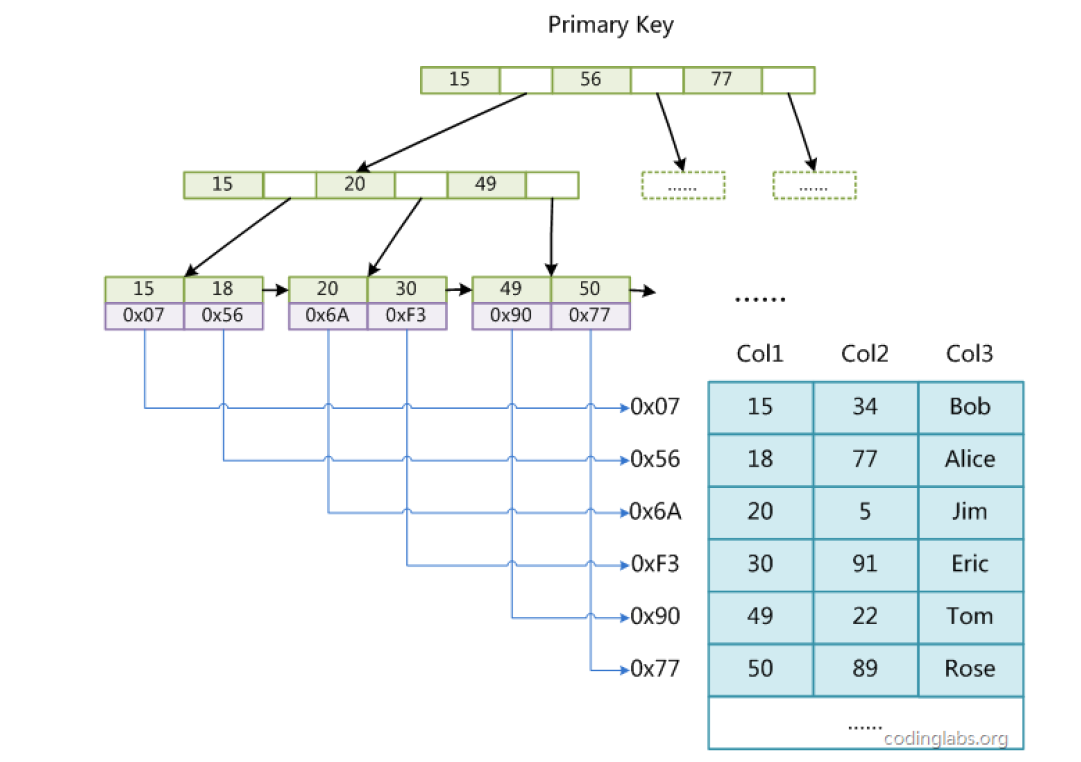
（3）辅助索引示意图

若在 Col2 上建立辅助索引，其结构如下：

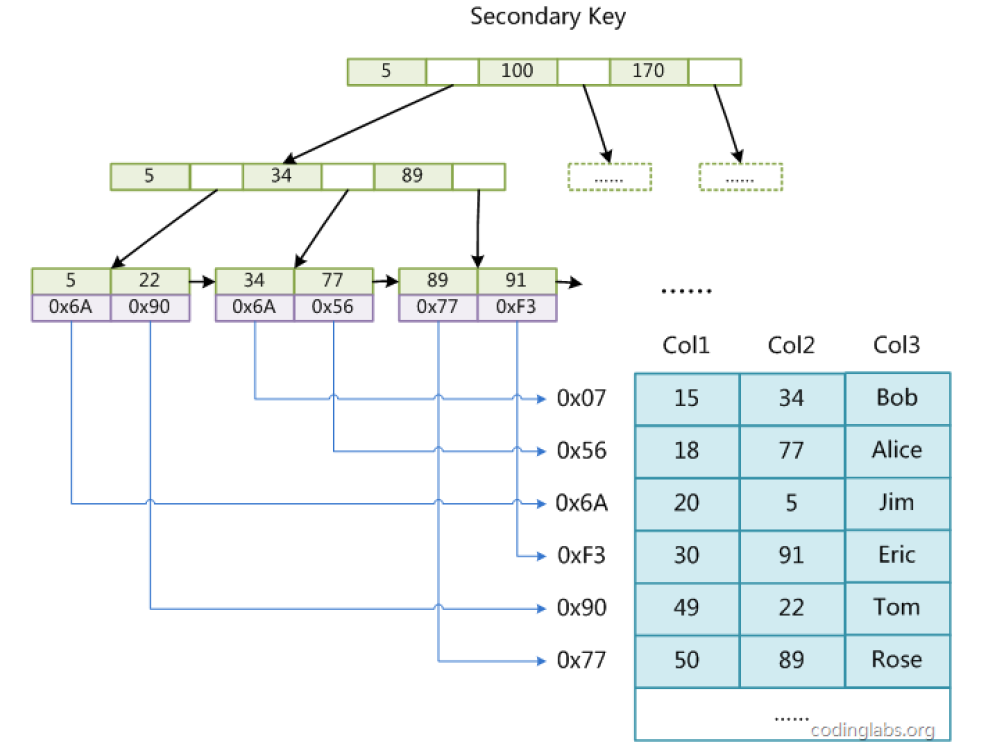
（4）查询流程

以查询 SELECT * FROM user WHERE Col2 = 77 为例，MyISAM 的查询流程：

访问辅助索引（Col2）的 B + 树，查找 key=77，得到数据记录的物理地址 0x56；

直接通过物理地址访问数据文件（.MYD），读取地址 0x56 对应的数据记录（18, 77, Alice）；

返回结果。

（5）核心特点

索引与数据分离，索引仅存储地址，结构简单；

主索引和辅助索引无本质区别，仅主索引要求关键字唯一；

查询时需要 "索引查找→地址访问" 两步，效率受磁盘地址访问速度影响；

不支持事务，崩溃后数据恢复困难。

5.3 InnoDB 存储引擎的 B + 树索引实现（聚集索引）

InnoDB 是 MySQL 5.5.8 版本之后的默认存储引擎，支持事务、行锁、外键，其索引实现采用聚集索引（Clustered Index），核心特点是 "数据文件本身就是索引文件"。

（1）核心设计理念

InnoDB 的核心设计：表数据文件（.ibd）本身就是一棵 B + 树，这棵树的叶子节点存储完整的数据记录，非叶子节点存储主键关键字和子节点指针。这意味着：

主索引就是数据文件，无需额外的索引文件；

所有数据记录都按照主键的顺序存储，主键的顺序就是数据的物理存储顺序。

（2）主索引（聚集索引）结构

沿用上面的数据，InnoDB 的主索引（以 Col1 为键）结构如下：

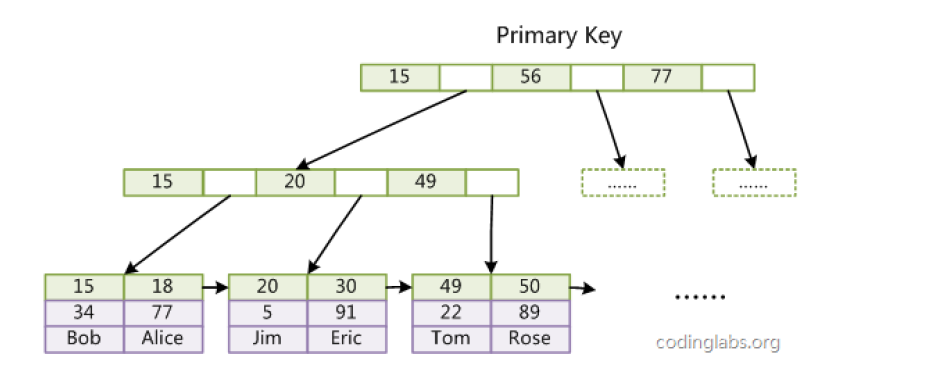
（3）辅助索引结构

InnoDB 的辅助索引与 MyISAM 的核心差异：辅助索引的叶子节点 data 域存储的是主键关键字，而非物理地址。

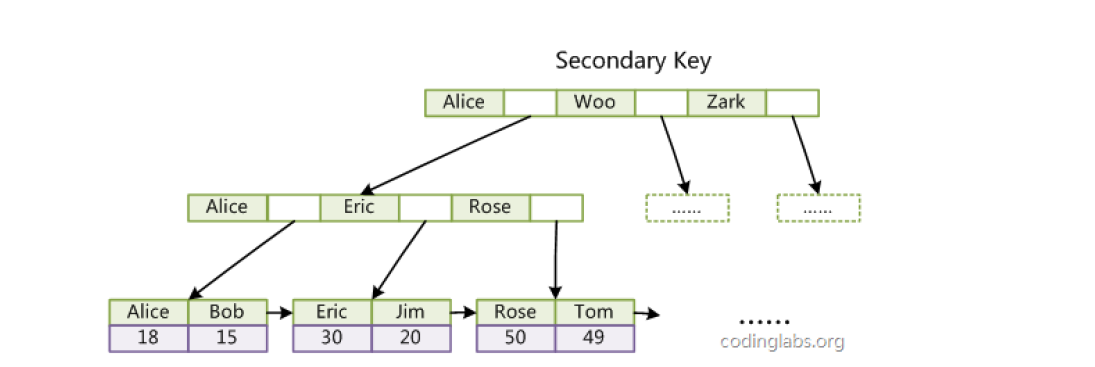
（4）查询流程

以查询SELECT * FROM user WHERE Col2 = 77为例，InnoDB 的查询流程（"回表查询"）：

访问辅助索引（Col2）的 B + 树，查找 key=77，得到对应的主键关键字 18；

访问主索引（聚集索引）的 B + 树，查找 key=18，得到完整的数据记录（18, 77, Alice）；

返回结果。

（5）核心特点

主索引与数据文件合一，查询主键时无需回表，效率极高；

辅助索引依赖主键，查询时需要 "辅助索引→主索引" 两步（回表），效率略低于 MyISAM，但事务支持更完善；

数据按照主键顺序存储，主键的选择对性能影响极大（建议使用自增主键，避免插入时频繁分裂节点）；

支持事务、行锁，崩溃后可通过事务日志恢复数据，可靠性更高。

5.4 两种存储引擎索引实现的核心差异

对比维度	MyISAM	InnoDB
索引类型	非聚集索引	聚集索引
索引与数据关系	索引文件与数据文件分离	数据文件本身就是主索引
主索引 data 域	物理地址	完整数据记录
辅助索引 data 域	物理地址	主键关键字
查询流程	索引查找→地址访问（一步）	辅助索引→主索引（回表，两步）
主键要求	可选，无强制要求	必须有主键（无显式则自动生成）
事务支持	不支持	支持
锁粒度	表锁	行锁
崩溃恢复	困难	支持（通过 redo/undo 日志）

5.5 实战建议：如何选择索引与存储引擎？

优先使用 InnoDB：支持事务、行锁，数据可靠性更高，适合大多数业务场景（如电商、金融、社交）；

主键设计 ：使用自增整数主键，避免使用字符串或随机数主键 ------ 自增主键能保证插入时数据顺序存储，减少节点分裂，提高插入效率；

辅助索引优化：避免过度创建辅助索引（每个辅助索引都会占用磁盘空间，且插入 / 更新时需要维护），针对频繁查询的字段建立索引；

范围查询优化：利用 B + 树的叶子节点链表特性，对于范围查询（如时间范围、数值范围），尽量使用主键或辅助索引的有序字段，减少回表次数。

六、C++ 实现简易 B + 树（索引核心功能）

为了让大家更深入地理解 B + 树的实现逻辑，我们用 C++ 编写一个简易的 B + 树模板类，实现核心的插入、查找、范围查询功能。

6.1 设计思路

节点类型：分为分支节点（非叶子节点）和叶子节点，采用继承体系实现；

关键字类型：模板参数 K，支持任意可比较类型；

数据存储：叶子节点存储 <K, V> 键值对，分支节点存储 <K, 子节点指针 >；

链表连接：叶子节点通过双向链表串联，支持范围查询；

核心功能：Insert（插入）、Find（单值查找）、RangeFind（范围查询）。

6.2 代码实现

cpp 复制代码

#include <iostream>
#include <vector>
#include <utility>
#include <algorithm>
#include <cassert>
using namespace std;

// 前向声明
template <class K, class V, int M = 3>
class BPlusTree;

// 节点基类
template <class K, class V, int M>
struct BPlusTreeNode {
    BPlusTreeNode() : _parent(nullptr) {}
    virtual ~BPlusTreeNode() {}

    BPlusTreeNode<K, V, M>* _parent; // 父节点指针
    size_t _size; // 关键字个数
};

// 叶子节点
template <class K, class V, int M>
struct BPlusTreeLeafNode : public BPlusTreeNode<K, V, M> {
    pair<K, V> _data[M]; // 存储键值对，最多M个
    BPlusTreeLeafNode<K, V, M>* _prev; // 前驱叶子节点
    BPlusTreeLeafNode<K, V, M>* _next; // 后继叶子节点

    BPlusTreeLeafNode() : _prev(nullptr), _next(nullptr) {
        this->_size = 0;
        this->_parent = nullptr;
    }

    // 查找key在叶子节点中的位置，返回索引（未找到返回-1）
    int FindKey(const K& key) {
        for (size_t i = 0; i < this->_size; ++i) {
            if (_data[i].first == key) {
                return i;
            }
        }
        return -1;
    }

    // 插入键值对，返回插入位置
    int Insert(const pair<K, V>& kv) {
        int end = this->_size - 1;
        // 有序插入（插入排序逻辑）
        while (end >= 0 && kv.first < _data[end].first) {
            _data[end + 1] = _data[end];
            --end;
        }
        _data[end + 1] = kv;
        ++this->_size;
        return end + 1;
    }
};

// 分支节点（非叶子节点）
template <class K, class V, int M>
struct BPlusTreeBranchNode : public BPlusTreeNode<K, V, M> {
    K _keys[M]; // 关键字，最多M个
    BPlusTreeNode<K, V, M>* _children[M]; // 子节点指针，最多M个

    BPlusTreeBranchNode() {
        this->_size = 0;
        this->_parent = nullptr;
        for (size_t i = 0; i < M; ++i) {
            _children[i] = nullptr;
        }
    }

    // 查找key对应的子节点指针索引
    int FindChildIndex(const K& key) {
        int index = this->_size - 1;
        while (index >= 0 && key < _keys[index]) {
            --index;
        }
        return index + 1; // 返回子节点指针索引
    }

    // 插入关键字和对应的子节点指针
    void Insert(const K& key, BPlusTreeNode<K, V, M>* child) {
        int end = this->_size - 1;
        while (end >= 0 && key < _keys[end]) {
            _keys[end + 1] = _keys[end];
            _children[end + 1] = _children[end];
            --end;
        }
        _keys[end + 1] = key;
        _children[end + 1] = child;
        child->_parent = this;
        ++this->_size;
    }
};

// B+树模板类
template <class K, class V, int M = 3>
class BPlusTree {
    typedef BPlusTreeNode<K, V, M> Node;
    typedef BPlusTreeLeafNode<K, V, M> LeafNode;
    typedef BPlusTreeBranchNode<K, V, M> BranchNode;

public:
    BPlusTree() : _root(nullptr) {}
    ~BPlusTree() {
        Destroy(_root);
    }

    // 插入键值对
    bool Insert(const K& key, const V& value) {
        // 树为空，创建根节点（叶子节点）
        if (_root == nullptr) {
            _root = new LeafNode;
            static_cast<LeafNode*>(_root)->Insert(make_pair(key, value));
            return true;
        }

        // 查找插入位置（叶子节点）
        LeafNode* leaf = FindLeafNode(key);
        // 关键字已存在，插入失败
        if (leaf->FindKey(key) != -1) {
            cout << "Key " << key << " already exists!" << endl;
            return false;
        }

        // 插入到叶子节点
        leaf->Insert(make_pair(key, value));
        // 检查叶子节点是否满
        if (leaf->_size < M) {
            return true;
        }

        // 叶子节点满，需要分裂
        SplitLeafNode(leaf);
        return true;
    }

    // 查找关键字对应的value，找到返回true，否则返回false
    bool Find(const K& key, V& value) {
        if (_root == nullptr) {
            return false;
        }

        LeafNode* leaf = FindLeafNode(key);
        int index = leaf->FindKey(key);
        if (index == -1) {
            return false;
        }

        value = leaf->_data[index].second;
        return true;
    }

    // 范围查询：查找[key1, key2]之间的所有键值对
    vector<pair<K, V>> RangeFind(const K& key1, const K& key2) {
        vector<pair<K, V>> result;
        if (_root == nullptr) {
            return result;
        }

        // 找到key1所在的叶子节点
        LeafNode* leaf = FindLeafNode(key1);
        while (leaf != nullptr) {
            // 遍历当前叶子节点的关键字
            for (size_t i = 0; i < leaf->_size; ++i) {
                K currentKey = leaf->_data[i].first;
                if (currentKey > key2) {
                    goto END; // 超出范围，退出
                }
                if (currentKey >= key1) {
                    result.push_back(leaf->_data[i]);
                }
            }
            // 遍历下一个叶子节点
            leaf = leaf->_next;
        }

    END:
        return result;
    }

    // 中序遍历（验证B+树有序性）
    void InOrder() {
        InOrder(_root);
        cout << endl;
    }

private:
    // 递归中序遍历
    void InOrder(Node* root) {
        if (root == nullptr) {
            return;
        }

        BranchNode* branch = dynamic_cast<BranchNode*>(root);
        if (branch != nullptr) {
            // 分支节点：遍历子节点
            for (size_t i = 0; i < branch->_size; ++i) {
                InOrder(branch->_children[i]);
                cout << branch->_keys[i] << " ";
            }
            InOrder(branch->_children[branch->_size]);
            return;
        }

        // 叶子节点：输出关键字
        LeafNode* leaf = dynamic_cast<LeafNode*>(root);
        for (size_t i = 0; i < leaf->_size; ++i) {
            cout << leaf->_data[i].first << " ";
        }
    }

    // 查找key对应的叶子节点
    LeafNode* FindLeafNode(const K& key) {
        Node* cur = _root;
        while (true) {
            BranchNode* branch = dynamic_cast<BranchNode*>(cur);
            if (branch == nullptr) {
                // 到达叶子节点
                return static_cast<LeafNode*>(cur);
            }
            // 分支节点，查找子节点索引
            int index = branch->FindChildIndex(key);
            cur = branch->_children[index];
        }
    }

    // 分裂叶子节点
    void SplitLeafNode(LeafNode* leaf) {
        // 创建新的叶子节点
        LeafNode* newLeaf = new LeafNode;
        // 分裂点：中间位置，前半部分留在原节点，后半部分移入新节点
        int mid = M / 2;
        for (int i = mid; i < leaf->_size; ++i) {
            newLeaf->_data[newLeaf->_size++] = leaf->_data[i];
        }
        // 更新原节点的关键字个数
        leaf->_size = mid;

        // 更新叶子节点的链表连接
        newLeaf->_prev = leaf;
        newLeaf->_next = leaf->_next;
        if (leaf->_next != nullptr) {
            leaf->_next->_prev = newLeaf;
        }
        leaf->_next = newLeaf;

        // 向上插入中间关键字到父节点
        K midKey = newLeaf->_data[0].first;
        InsertToParent(leaf, midKey, newLeaf);
    }

    // 向上插入关键字到父节点
    void InsertToParent(Node* leftChild, const K& key, Node* rightChild) {
        Node* parent = leftChild->_parent;
        // 父节点为空（原节点是根节点），创建新的根节点（分支节点）
        if (parent == nullptr) {
            BranchNode* newRoot = new BranchNode;
            newRoot->Insert(key, rightChild);
            newRoot->_children[0] = leftChild;
            leftChild->_parent = newRoot;
            rightChild->_parent = newRoot;
            newRoot->_size = 1;
            _root = newRoot;
            return;
        }

        // 父节点是分支节点，插入关键字和子节点
        BranchNode* branchParent = dynamic_cast<BranchNode*>(parent);
        branchParent->Insert(key, rightChild);
        // 检查父节点是否满
        if (branchParent->_size < M) {
            return;
        }

        // 父节点满，分裂分支节点
        SplitBranchNode(branchParent);
    }

    // 分裂分支节点
    void SplitBranchNode(BranchNode* branch) {
        // 创建新的分支节点
        BranchNode* newBranch = new BranchNode;
        // 分裂点：中间位置，前半部分留在原节点，后半部分移入新节点
        int mid = M / 2;
        K midKey = branch->_keys[mid]; // 上升到父节点的关键字

        // 搬移关键字和子节点指针
        for (int i = mid + 1; i < branch->_size; ++i) {
            newBranch->_keys[newBranch->_size] = branch->_keys[i];
            newBranch->_children[newBranch->_size] = branch->_children[i];
            newBranch->_children[newBranch->_size]->_parent = newBranch;
            ++newBranch->_size;
        }
        // 搬移最后一个子节点指针
        newBranch->_children[newBranch->_size] = branch->_children[branch->_size];
        if (newBranch->_children[newBranch->_size] != nullptr) {
            newBranch->_children[newBranch->_size]->_parent = newBranch;
        }

        // 更新原节点的关键字个数
        branch->_size = mid;

        // 向上插入中间关键字到父节点
        InsertToParent(branch, midKey, newBranch);
    }

    // 销毁树（递归释放节点）
    void Destroy(Node* root) {
        if (root == nullptr) {
            return;
        }

        BranchNode* branch = dynamic_cast<BranchNode*>(root);
        if (branch != nullptr) {
            for (size_t i = 0; i <= branch->_size; ++i) {
                Destroy(branch->_children[i]);
            }
        }

        delete root;
        root = nullptr;
    }

private:
    Node* _root; // B+树根节点
};

// 测试代码
int main() {
    // 创建3阶B+树（叶子节点最多存储2个键值对）
    BPlusTree<int, string, 3> bpt;

    // 插入测试数据
    bpt.Insert(5, "Jim");
    bpt.Insert(10, "Tom");
    bpt.Insert(20, "Alice");
    bpt.Insert(28, "Bob");
    bpt.Insert(35, "Eric");
    bpt.Insert(56, "Rose");
    bpt.Insert(65, "Lily");
    bpt.Insert(80, "Jack");
    bpt.Insert(90, "Lucy");

    // 中序遍历（预期输出：5 10 20 28 35 56 65 80 90）
    cout << "B+树中序遍历结果：";
    bpt.InOrder();

    // 单值查找
    string value;
    if (bpt.Find(28, value)) {
        cout << "Find key=28, value=" << value << endl;
    } else {
        cout << "Key=28 not found!" << endl;
    }

    // 范围查询（key=20~65）
    vector<pair<int, string>> rangeResult = bpt.RangeFind(20, 65);
    cout << "RangeFind [20, 65] result：";
    for (auto& kv : rangeResult) {
        cout << "(" << kv.first << ", " << kv.second << ") ";
    }
    cout << endl;

    // 插入重复关键字
    bpt.Insert(28, "Bob2");

    return 0;
}

6.3 测试结果

运行测试代码后，输出如下：

复制代码

B+树中序遍历结果：5 10 20 28 35 56 65 80 90 
Find key=28, value=Bob
RangeFind [20, 65] result：(20, Alice) (28, Bob) (35, Eric) (56, Rose) (65, Lily) 
Key 28 already exists!

测试结果说明：

中序遍历结果有序，验证了 B + 树的关键字有序性；

单值查找能正确找到对应的 value；

范围查询能高效返回指定区间的键值对；

重复关键字插入失败，符合索引唯一性要求。

总结

从 B 树到 B + 树，再到 B * 树，每一次进化都是为了更好地适应外部存储场景的需求 ------ 核心目标始终是 "减少磁盘 IO、提高检索效率、优化空间利用率"。而 MySQL 的索引实现，则是将这些数据结构理论与实际业务场景深度结合的典范。

数据结构是程序的骨架，而 B 树家族则是骨架中最坚硬的部分之一。掌握它们的设计原理与应用场景，不仅能帮助你在面试中脱颖而出，更能让你在实际开发中写出更高效、更可靠的代码。如果你有任何疑问或想要深入探讨某个知识点，欢迎在评论区留言交流～