n 维向量及其运算
n 维向量是线性代数的核心基础概念之一,也是 AI 领域中数据表示、特征提取、模型计算 的核心载体(例如机器学习中用 n 维向量表示样本的特征)。以下从定义、核心运算、运算性质、应用场景四个维度展开,结合推导和示例进行详细讲解。
一、n 维向量的定义
1. 基本定义
由 n 个实数 a1,a2,...,an 组成的有序数组,称为 n 维实向量,记作:
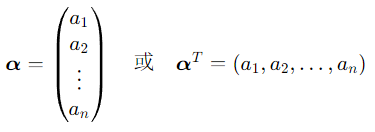
- 前者称为 n 维列向量(默认形式,与矩阵运算兼容性更好);
- 后者称为 n 维行向量(列向量的转置);
- ai 称为向量 α 的第 i 个分量(或坐标)。
2. 特殊向量

3. 向量相等的条件
两个 n 维向量 α=(a1,a2,...,an)T 和 β=(b1,b2,...,bn)T 相等,当且仅当对应分量全部相等,即:
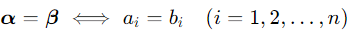
二、n 维向量的核心运算
n 维向量的运算分为 ** 线性运算(加法、数乘)和非线性运算(内积、范数)** 两大类,其中线性运算是向量空间的基础,内积和范数则是度量向量关系的核心工具。
1. 线性运算:加法与数乘
(1)向量加法
定义:设两个 n 维列向量 α=(a1,a2,...,an)T,β=(b1,b2,...,bn)T,则它们的和为:
(3)线性运算的性质
设 α,β,γ 为 n 维向量,k,l 为实数,则满足以下 8 条运算律(构成向量空间的核心条件):
- 交换律:α+β=β+α
- 结合律:(α+β)+γ=α+(β+γ)
- 零向量存在:α+0=α
- 负向量存在:α+(−α)=0
- 数乘单位律:1⋅α=α
- 数乘结合律:k(lα)=(kl)α
- 数乘分配律 1:k(α+β)=kα+kβ
- 数乘分配律 2:(k+l)α=kα+lα