【1】41. 缺失的第一个正数
日期：12.16
https://leetcode.cn/problems/first-missing-positive/description/?envType=problem-list-v2&envId=array2.类型：数组，哈希表
3.方法一：哈希表（官方题解）
算法思想：
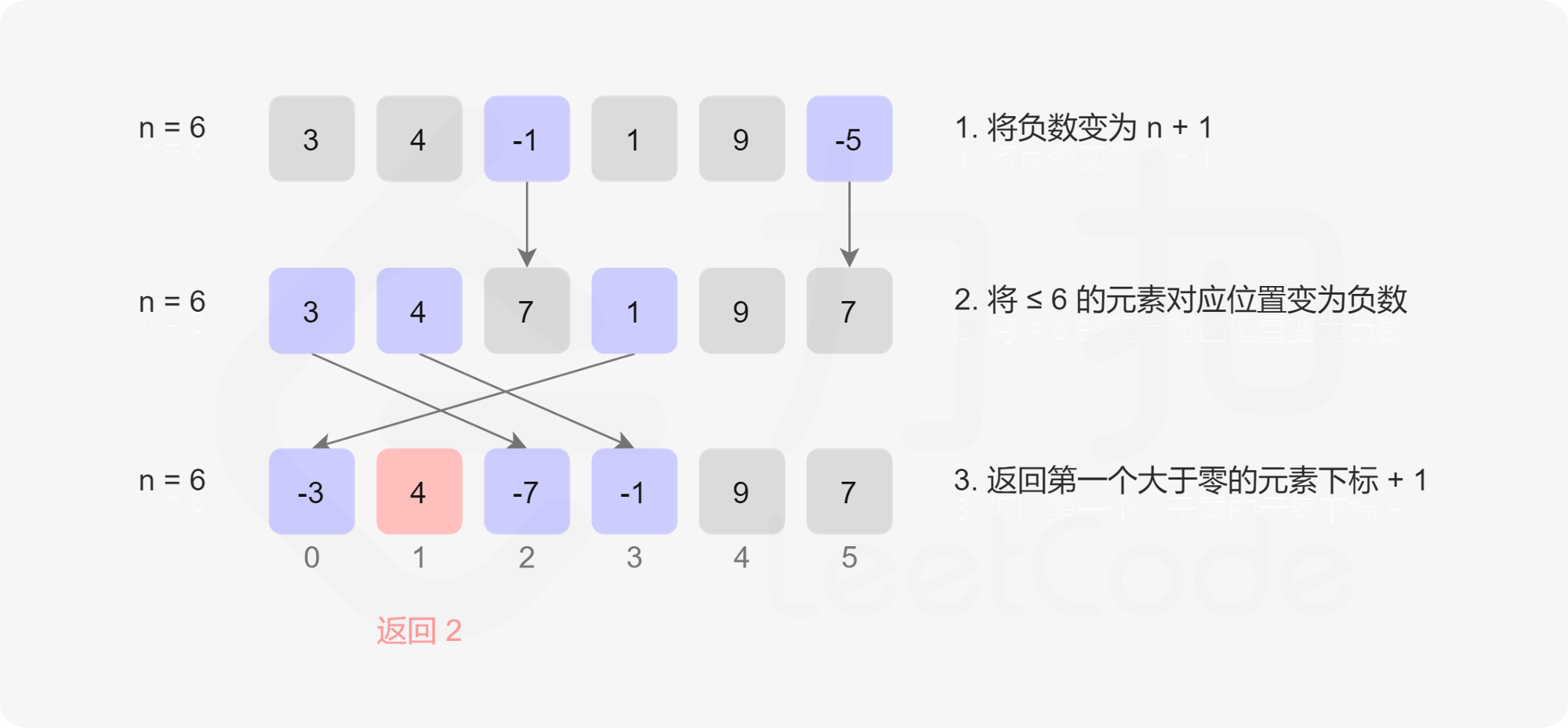
对于一个长度为 N 的数组，其中没有出现的最小正整数只能在 [1,N+1] 中。这是因为如果 [1,N] 都出现了，那么答案是 N+1，否则答案是 [1,N] 中没有出现的最小正整数。对数组进行遍历，对于遍历到的数 x，如果它在 [1,N] 的范围内，那么就将数组中的第 x−1 个位置（注意：数组下标从 0 开始）打上「标记」。在遍历结束之后，如果所有的位置都被打上了标记，那么答案是 N+1，否则答案是最小的没有打上标记的位置加 1。
算法的流程：
可以继续利用上面的提到的性质：可以先对数组进行遍历，把不在 [1,N] 范围内的数修改成任意一个大于 N 的数（例如 N+1）。这样一来，数组中的所有数就都是正数了，就可以将「标记」表示为「负号」。
关键代码：
cpp
// 第一步：将所有非正数（负数和0）替换为 n+1
for(int& num: nums){
if(num<=0){
num=n+1;
}
}
// 第二步：遍历数组，将出现的数字标记为负数
for(int i=0;i<n;++i){
int num=abs(nums[i]);
if(num<=n){
nums[num-1]=-abs(nums[num-1]);
}
}
// 第三步：找到第一个正数的位置
for(int i=0;i<n;++i){
if(nums[i]>0){
// 如果 nums[i] > 0，说明数字 i+1 没有出现过
return i+1;
}
}
// 如果所有位置都是负数，说明 1 到 n 都出现过
// 那么缺失的第一个正数就是 n+1
return n + 1;4.方法二：置换（半解）
如果数组中包含 x∈[1,N]，那么恢复后，数组的第 x−1 个元素为 x。
在恢复后，数组应当有 [1, 2, ..., N] 的形式，但其中有若干个位置上的数是错误的，每一个错误的位置就代表了一个缺失的正数。以题目中的示例二 [3, 4, -1, 1] 为例，恢复后的数组应当为 [1, -1, 3, 4]，可以知道缺失的数为 2。
可以对数组进行一次遍历，对于遍历到的数 x=nums[i]，如果 x∈[1,N]，就知道 x 应当出现在数组中的 x−1 的位置，因此交换 nums[i] 和 nums[x−1]，这样 x 就出现在了正确的位置。在完成交换后，新的 nums[i] 可能还在 [1,N] 的范围内，需要继续进行交换操作，直到 x∈/[1,N]。
当 nums[i]=x=nums[x−1]，说明 x 已经出现在了正确的位置。因此我们可以跳出循环，开始遍历下一个数。
关键代码：
cpp
// 第一步：将每个正整数放到正确的位置
for(int i=0;i<n;++i){
// 当当前位置的数字在[1, n]范围内，且不在正确位置上时，进行交换
while(nums[i]>0&&nums[i]<=n&&nums[nums[i]-1]!=nums[i]){
swap(nums[nums[i]-1],nums[i]);
}
}
// 第二步：寻找第一个位置不正确的数字
for(int i=0;i<n;++i){
if(nums[i]!=i+1){
return i+1;
}
}
return n+1;【2】46. 全排列
日期：12.17
2.类型：数组，回溯
3.方法一：回溯（官方题解）
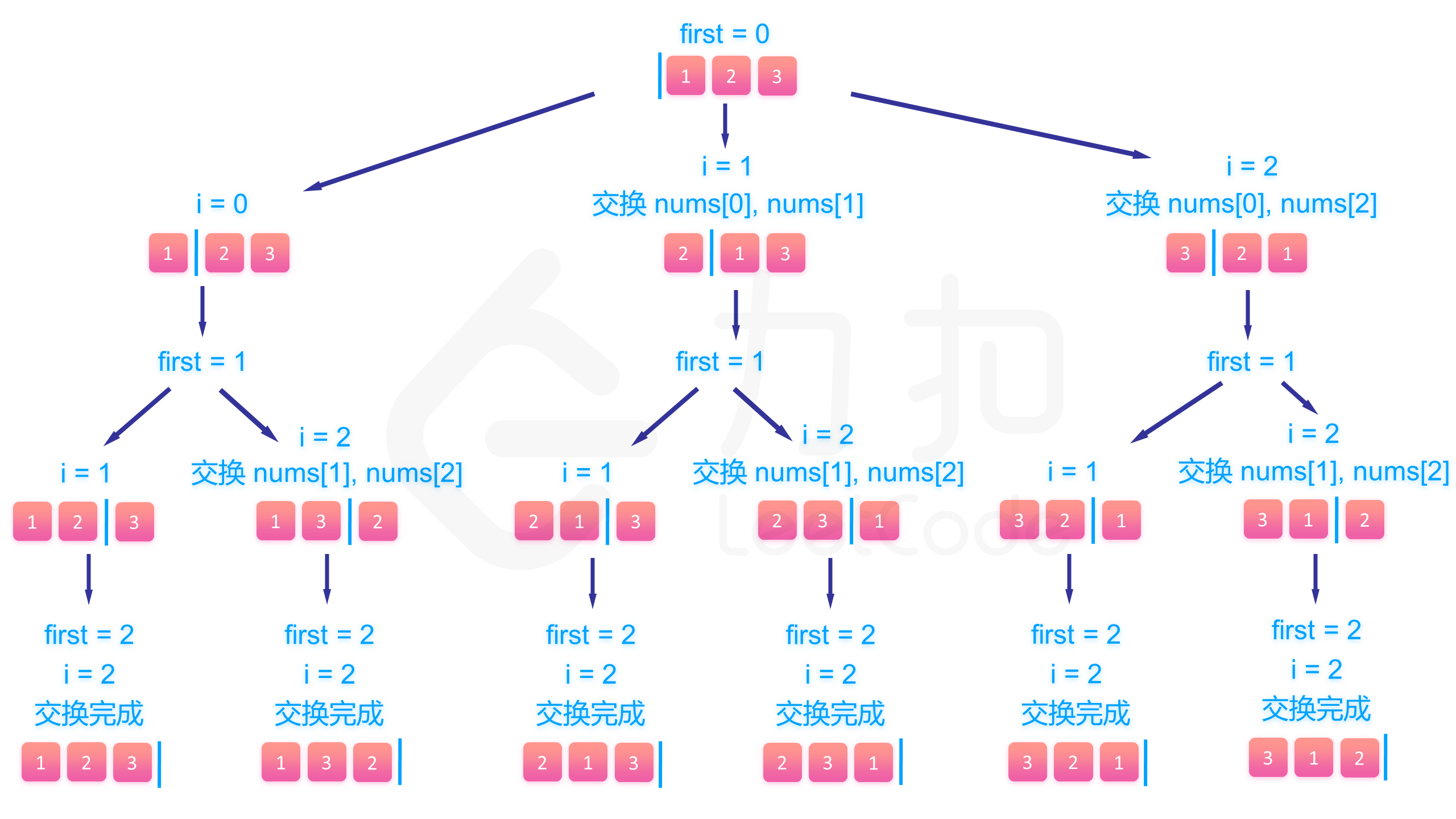
假设已经填到第 first 个位置，那么 nums 数组中 [0,first−1] 是已填过的数的集合，[first,n−1] 是待填的数的集合。尝试用 [first,n−1] 里的数去填第 first 个数，假设待填的数的下标为 i，那么填完以后我们将第 i 个数和第 first 个数交换，即能使得在填第 first+1 个数的时候 nums 数组的 [0,first] 部分为已填过的数，[first+1,n−1] 为待填的数，回溯的时候交换回来即能完成撤销操作。
关键代码：
cpp
// 遍历从当前位置到末尾的所有可能选择
for(int i=first;i<len;++i){
// 交换：将第i个元素放到当前位置first
swap(output[i],output[first]);
// 递归：处理下一个位置
backtrack(res,output,first+1,len);
// 回溯：撤销交换，恢复原状
swap(output[i], output[first]);
}
}【3】47. 全排列 II
日期：12.18
2.类型：数组，回溯
3.方法一：回溯（半解）
核心思想：对于相同数字，我们保证它们的使用顺序是从左到右的。
如果前一个相同数字没有被使用（!vis[i - 1]），那么当前数字不能使用
这样确保在树的同一层，相同的数字只会被选择一次
避免了因为顺序不同而产生的重复排列
关键代码：
cpp
for(int i=0;i<(int)nums.size();++i){
// 剪枝条件1：该数字已被使用
// 剪枝条件2：避免重复排列的关键条件
if(vis[i] || (i > 0 && nums[i]==nums[i-1]&&!vis[i-1])){
continue;
}
perm.emplace_back(nums[i]);
vis[i]=1; // 标记为已使用
backtrack(nums,ans,idx+1,perm);
vis[i]=0;
perm.pop_back();
}
}【4】57. 插入区间
日期：12.19
2.类型：数组，模拟
3.方法一：模拟（半解）
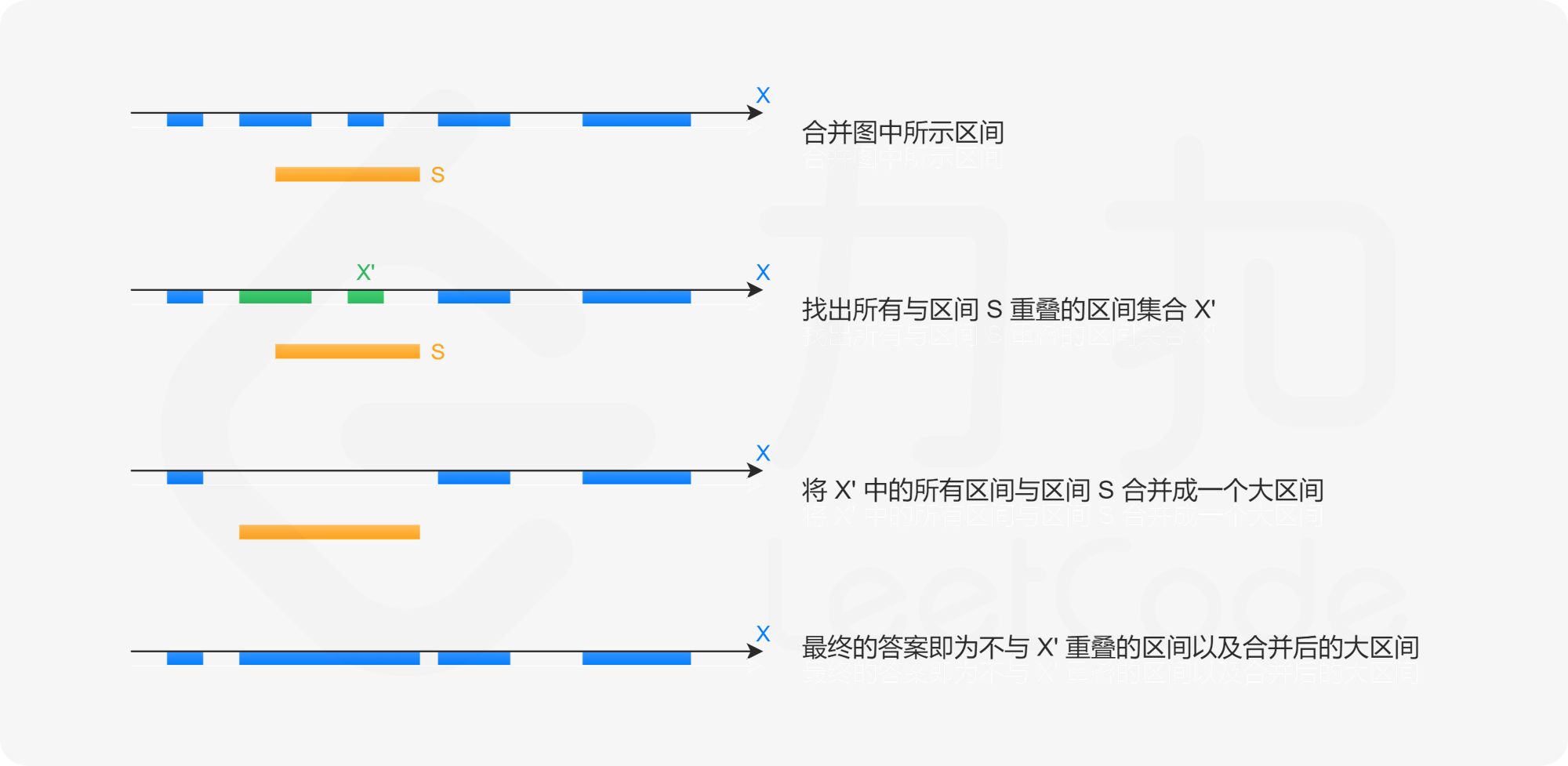
在给定的区间集合 X 互不重叠的前提下，当需要插入一个新的区间 S=[left,right] 时，只需要：
找出所有与区间 S 重叠的区间集合 X ′ ；
将 X ′中的所有区间连带上区间 S 合并成一个大区间；
最终的答案即为不与 X ′重叠的区间以及合并后的大区间。
当遍历到区间 [l i,r i] 时：
如果 r i<left，说明 [l i,r i] 与 S 不重叠并且在其左侧，可以直接将 [l i,r i] 加入答案；
如果 l i>right，说明 [l i,r i] 与 S 不重叠并且在其右侧，可以直接将 [l i,r i] 加入答案；
如果上面两种情况均不满足，说明 [l i,r i] 与 S 重叠，无需将 [li,ri] 加入答案。此时，需要将 S 与 [li,ri] 合并，即将 S 更新为其与 [li,ri] 的并集。
关键代码：
cpp
for(const auto& interval:intervals){
if(interval[0]>right){
// 情况1：当前区间在新区间的右侧且无交集
if(!placed){
// 如果新区间还没插入，先插入新区间
ans.push_back({left,right});
placed=true;
}
// 然后插入当前区间
ans.push_back(interval);
}
else if(interval[1]<left){
// 情况2：当前区间在新区间的左侧且无交集
// 直接插入当前区间
ans.push_back(interval);
}
else {
// 情况3：当前区间与新区间有交集
// 合并区间：更新新区间的左右端点
left=min(left, interval[0]);
right=max(right, interval[1]);
}
}
// 如果遍历结束后新区间还没插入（可能在最后面）
if(!placed){
ans.push_back({left,right});
}【5】88. 合并两个有序数组
日期：12.20
2.类型：数组，排序
3.方法一：直接合并后排序（一次题解）
先将数组 nums2 放进数组 nums1 的尾部，然后直接对整个数组进行排序。
关键代码：
cpp
for(int i=0;i<n;++i){
nums1[m+i]=nums2[i];
}
sort(nums1.begin(),nums1.end());【6】75. 颜色分类
日期：12.21
2.类型：数组，双指针
3.方法一：单指针（一次题解）
第一次遍历：处理所有的 0
将所有的 0 交换到数组开头
遍历结束后，前 ptr 个位置都是 0
第二次遍历：处理所有的 1
从 ptr 开始（跳过已放置的 0）
将所有的 1 交换到 0 后面
遍历结束后，ptr 指向 1 的末尾
关键代码:
cpp
for(int i=0;i<n;++i){
if(nums[i]==0){
swap(nums[i],nums[ptr]);
++ptr;
}
}
for (int i=ptr;i<n;++i){
if(nums[i]==1){
swap(nums[i],nums[ptr]);
++ptr;
}
}【7】78. 子集
日期：12.22
2.类型：数组，位运算
3.方法一：迭代法实现子集枚举（官方题解）
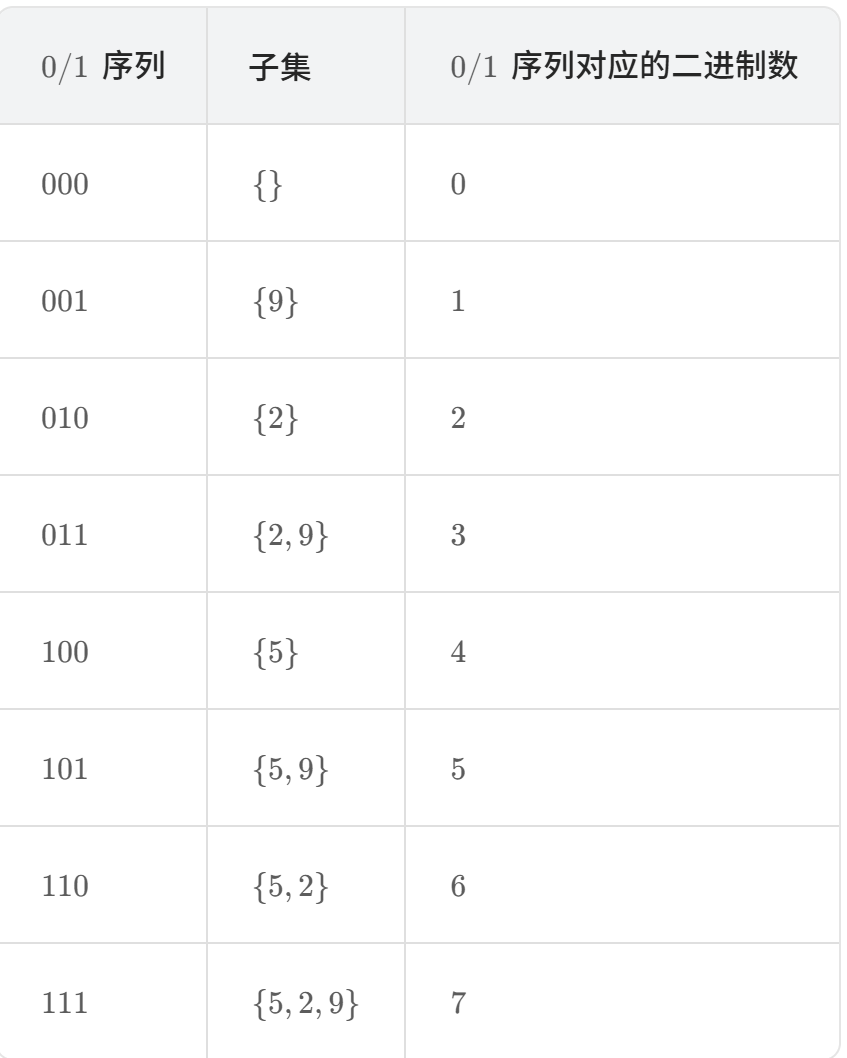
记原序列中元素的总数为 n。原序列中的每个数字 ai的状态可能有两种，即「在子集中」和「不在子集中」。用 1 表示「在子集中」，0 表示不在子集中，那么每一个子集可以对应一个长度为 n 的 0/1 序列，第 i 位表示 ai是否在子集中。例如，n=3 ，a={5,2,9} 时：
关键代码：
cpp
// 遍历所有可能的掩码（0 到 2^n - 1）
// 1 << n 等于 2^n
for(int mask=0;mask<(1 << n); ++mask){
t.clear(); // 清空临时子集，准备构建新的子集
for(int i=0;i<n;++i){
// (1 << i) 创建一个只有第i位为1的二进制数
// mask & (1 << i) 检查mask的第i位是否为1
// 如果为1，表示选择nums[i]加入子集
if mask &(1 << i)){
t.push_back(nums[i]);
}
}
ans.push_back(t);
}日期：12.23
2.类型：数组，哈希表
3.方法一：哈希表（一次题解）
使用哈希映射统计数组中每个元素的出现次数。对于哈希映射中的每个键值对，键表示一个元素，值表示其出现的次数。在统计完成后，遍历哈希映射即可找出只出现一次的元素。
关键代码：
cpp
for(int num: nums){
++freq[num];
}
int ans=0;
for(auto [num, occ]: freq){
if(occ==1){
ans=num;
break;
}
}【9】162. 寻找峰值
日期：12.24
2.类型：数组，二分查找，枚举
3.方法一：寻找最大值（一次题解）
由于题目保证了 nums[i]！=nums[i+1]，那么数组 nums 中最大值两侧的元素一定严格小于最大值本身。因此，最大值所在的位置就是一个可行的峰值位置。
关键代码：
cpp
return max_element(nums.begin(), nums.end()) - nums.begin();4.方法二：迭代爬坡（半解）
因此，首先在 [0,n) 的范围内随机一个初始位置 i，随后根据 nums[i−1],nums[i],nums[i+1] 三者的关系决定向哪个方向走：
如果 nums[i−1]<nums[i]>nums[i+1]，那么位置 i 就是峰值位置，直接返回 i 作为答案；
如果 nums[i−1]<nums[i]<nums[i+1]，那么位置 i 处于上坡，需要往右走，即 i←i+1；
如果 nums[i−1]>nums[i]>nums[i+1]，那么位置 i 处于下坡，需要往左走，即 i←i−1；
如果 nums[i−1]>nums[i]<nums[i+1]，那么位置 i 位于山谷，两侧都是上坡，可以朝任意方向走。
如果规定对于最后一种情况往右走，那么当位置 i 不是峰值位置时：
如果 nums[i]<nums[i+1]，那么往右走；
如果 nums[i]>nums[i+1]，那么往左走。
关键代码：
cpp
while(!(get(idx-1)<get(idx) && get(idx)>get(idx+1))){
if(get(idx)<get(idx+1)){
// 右侧更高，向右移动
idx+=1;
}else{
// 左侧更高（或相等），向左移动
idx-=1;
}
}【10】174. 地下城游戏
日期：12.25
2.类型：数组，动态规划
3.方法一：动态规划（官方题解）
公式推导
minn：从 (i,j) 的右边或下边到达终点所需的最小生命值
minn - dungeon[i][j]：
如果 dungeon[i][j] 是正数（加血）：所需初始生命值减少
如果 dungeon[i][j] 是负数（扣血）：所需初始生命值增加
max(..., 1)：保证生命值至少为1
问题转化：将"从起点到终点"转化为"从终点到起点"
状态设计：dp[i][j] 表示从 (i,j) 到终点所需的最小生命值
状态转移：dp[i][j] = max(min(dp[i+1][j], dp[i][j+1]) - dungeon[i][j], 1)
边界处理：使用虚拟位置和 INT_MAX 简化边界条件
关键代码：
cpp
// 终点右边和下边的位置设为1
dp[n][m-1]=dp[n-1][m]=1;
// 从终点(n-1,m-1)反向计算到起点(0,0)
for(int i=n-1;i>=0;--i){
for(int j=m-1;j>=0;--j){
// 选择向右或向下所需生命值较小的路径
int minn=min(dp[i+1][j], dp[i][j+1]);
// 公式：max(1, minn-dungeon[i][j])
dp[i][j]=max(minn-dungeon[i][j], 1);
}
}