计算机组成原理(10):逻辑门电路
(友情提示,本文为数字电路基础补充,有基础的可以跳过)
开篇:你以为你在写 if (a && b),其实你是在操控电流!
大家好!想问大家一个小问题------在 CPU 的硅片里,那些"0"和"1"到底是怎么被"算"出来的呢。
有人知道吗?当你写下这行 C 代码:
c
if (x > 0 && y < 100) { ... }编译器会把它翻译成一条条机器指令,而最终,这些逻辑判断会变成数以亿计的晶体管开关动作 。而连接这些晶体管的,正是我们今天要讲的主角------逻辑门电路 。

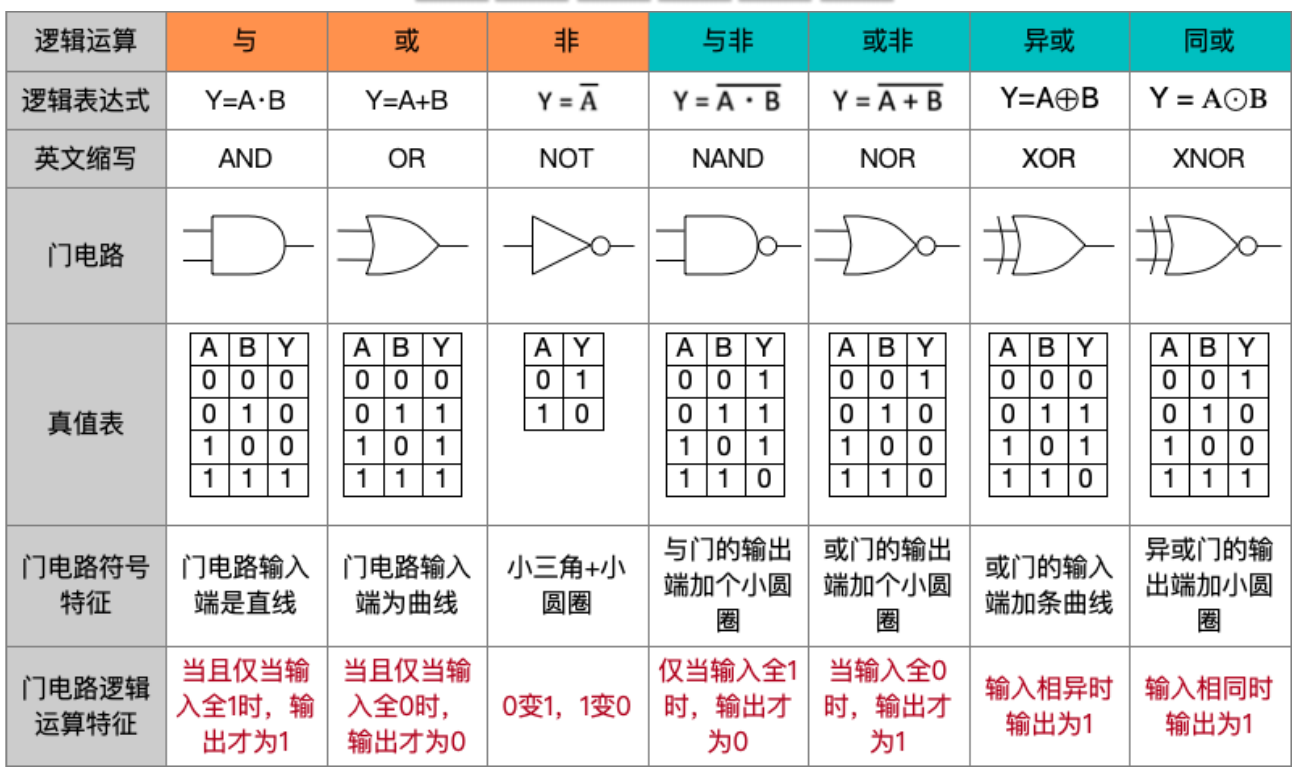
逻辑门电路是用于处理二进制的逻辑运算的,基本的逻辑运算包括与、或、非这样的三种。
而由这三种逻辑运算,可以组合形成更复杂的复合逻辑运算。比如说、与非、或非,异或和同或。当然,还有其他更复杂的复合逻辑运算,
希望大家别被"数字电路"吓到!本文将用最直观的方式 ,带你从"与或非"三大基本门出发,一路构建出异或门、同或门,甚至告诉你:为什么现代芯片能塞下上百亿个晶体管?
准备好了吗?Let's go!
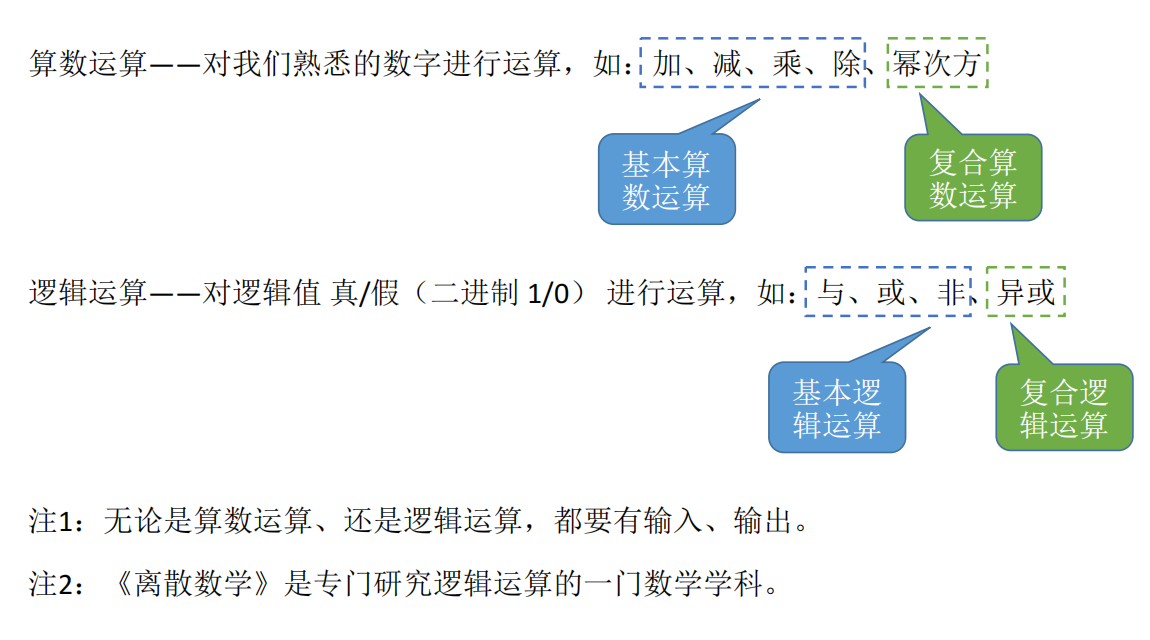
一、逻辑运算 vs 算术运算:两种世界的对话
1.1 算术运算:处理"连续"的世界
我们熟悉的加减乘除,操作对象是实数 (如 3.14、-5、1000)。比如:
x 3 = x × x × x x^3 = x \times x \times x x3=x×x×x
幂运算是复合算术运算,由多个乘法组合而成。
1.2 逻辑运算:处理"离散"的世界
而计算机的世界只有两个值:真(1)和假(0)。所有逻辑判断,最终都归结为对这两个值的操作。
💡 关键类比:
- 算术的基本运算是 +、−、×、÷
- 逻辑的基本运算是 与(AND)、或(OR)、非(NOT)
而且,就像 x 3 x^3 x3 可由乘法构建一样,所有复杂逻辑(如异或、同或)都可由 AND、OR、NOT 组合而成 !
二、三大基本逻辑门:数字世界的"原子"
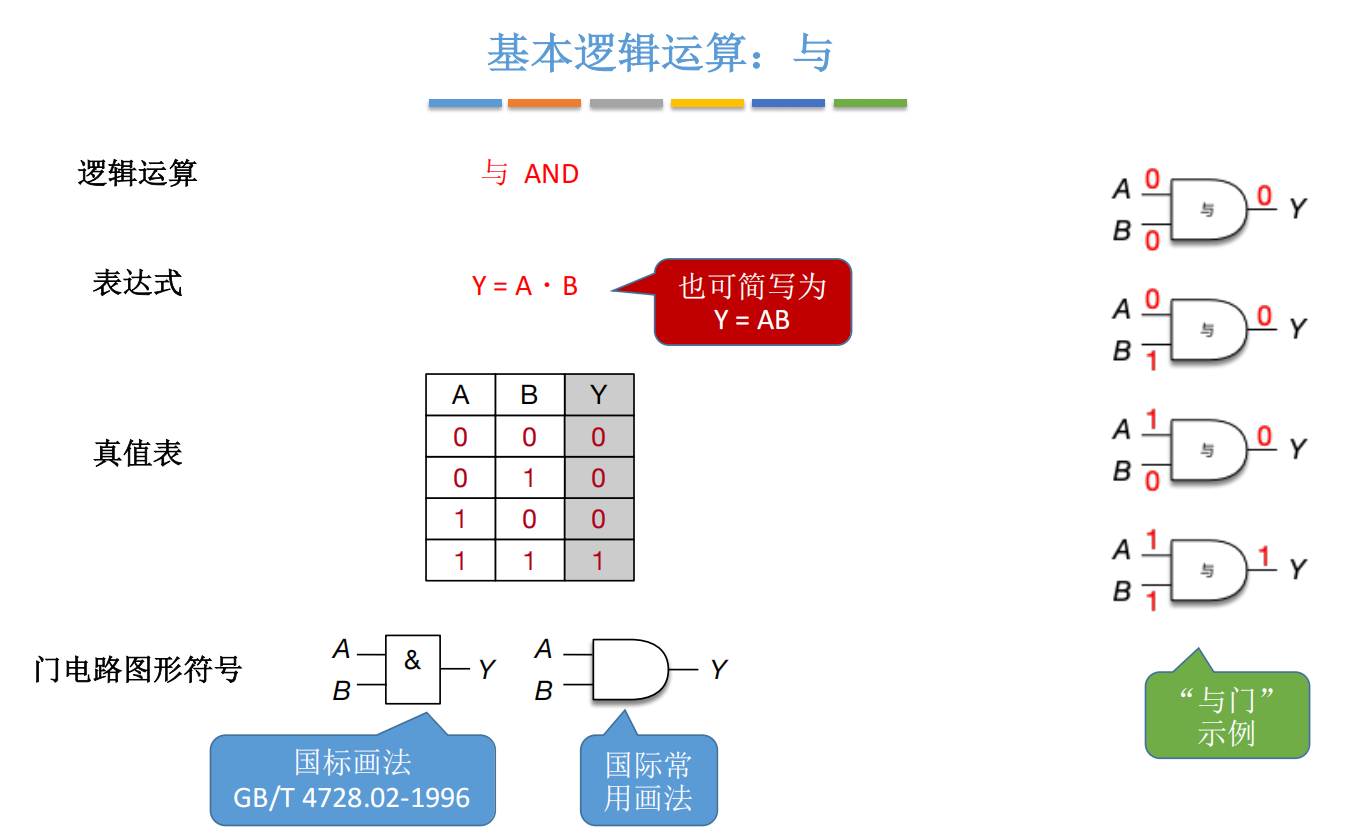
2.1 与门(AND Gate)------ "全都要,才给过"
逻辑表达式 :
Y = A ⋅ B 或简写为 Y = A B Y = A \cdot B \quad \text{或简写为} \quad Y = AB Y=A⋅B或简写为Y=AB
真值表:
| A | B | Y = A·B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
✅ 规则 :只有 A 和 B 同时为 1 ,输出才为 1。
🔁 C 语言类比 :
if (a && b)------ 两个条件都为真,才执行。
电路符号:
- 国标:矩形带"&"
- 国际通用 :输入端为直线 ,输出端为尖角
``
图示说明 :左侧为国标画法(矩形内写"&"),右侧为国际标准(DIN/IEEE)画法,输入为直线,输出为锥形。重点记忆:与门 = 直线输入。
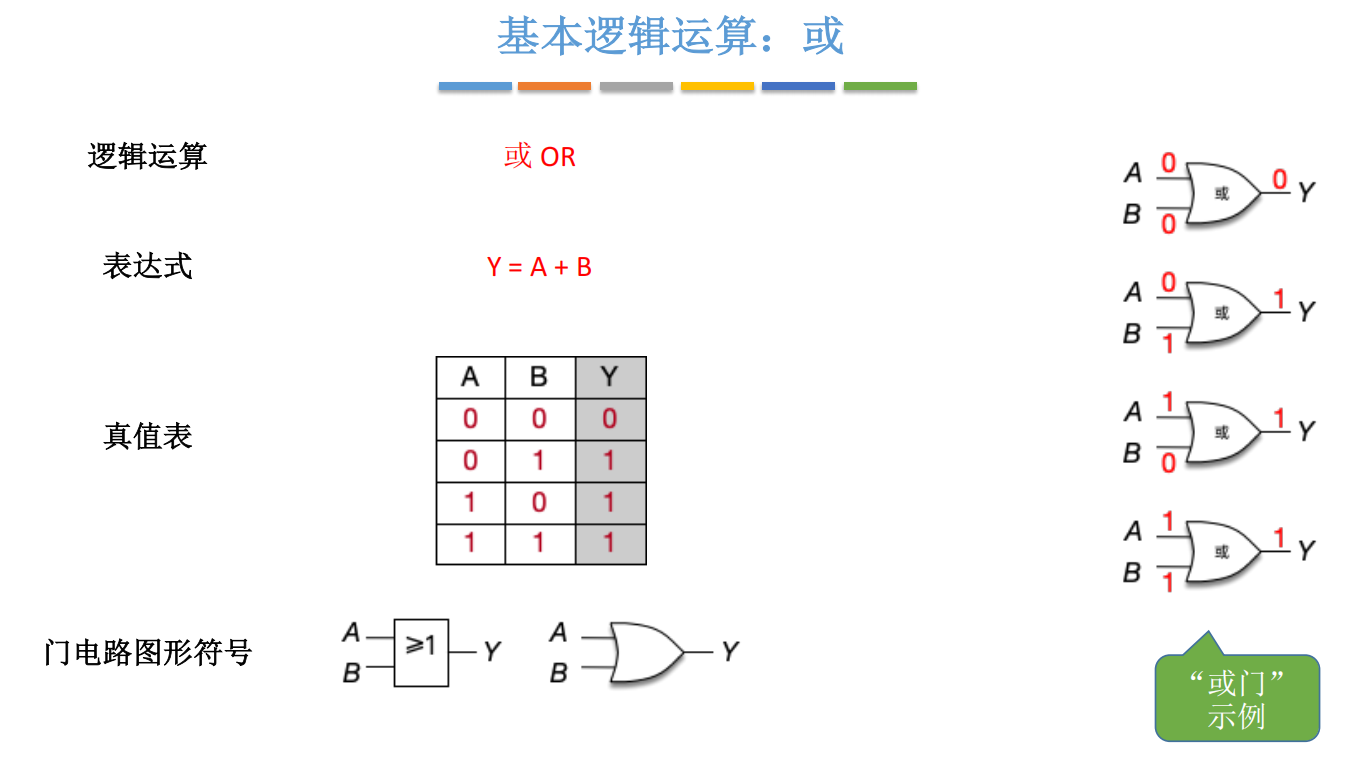
2.2 或门(OR Gate)------ "有一个就行"
逻辑表达式 :
Y = A + B (注意:这里的"+"读作"或",不是加法!) Y = A + B \quad \text{(注意:这里的"+"读作"或",不是加法!)} Y=A+B(注意:这里的"+"读作"或",不是加法!)
真值表:
| A | B | Y = A+B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
✅ 规则 :只要 A 或 B 有一个为 1 ,输出就是 1。
🔁 C 语言类比 :
if (a || b)
电路符号:
- 输入端为弧线(像微笑的嘴巴 😊)
- 输出端形状可变(圆、尖、平),但输入弧线是识别关键
``
图示说明 :或门输入端呈明显弧形,与与门的直线形成鲜明对比。记住口诀:"或弯与直"。
2.3 非门(NOT Gate)------ "唱反调专家"
逻辑表达式 :
Y = A ‾ Y = \overline{A} Y=A
真值表:
| A | Y = A ‾ \overline{A} A |
|---|---|
| 0 | 1 |
| 1 | 0 |
规则 :输入 0 → 输出 1;输入 1 → 输出 0。取反!
电路符号:
- 一个三角形 + 输出端的小圆圈(●)
- 小圆圈也可出现在输入端(表示"低电平有效")
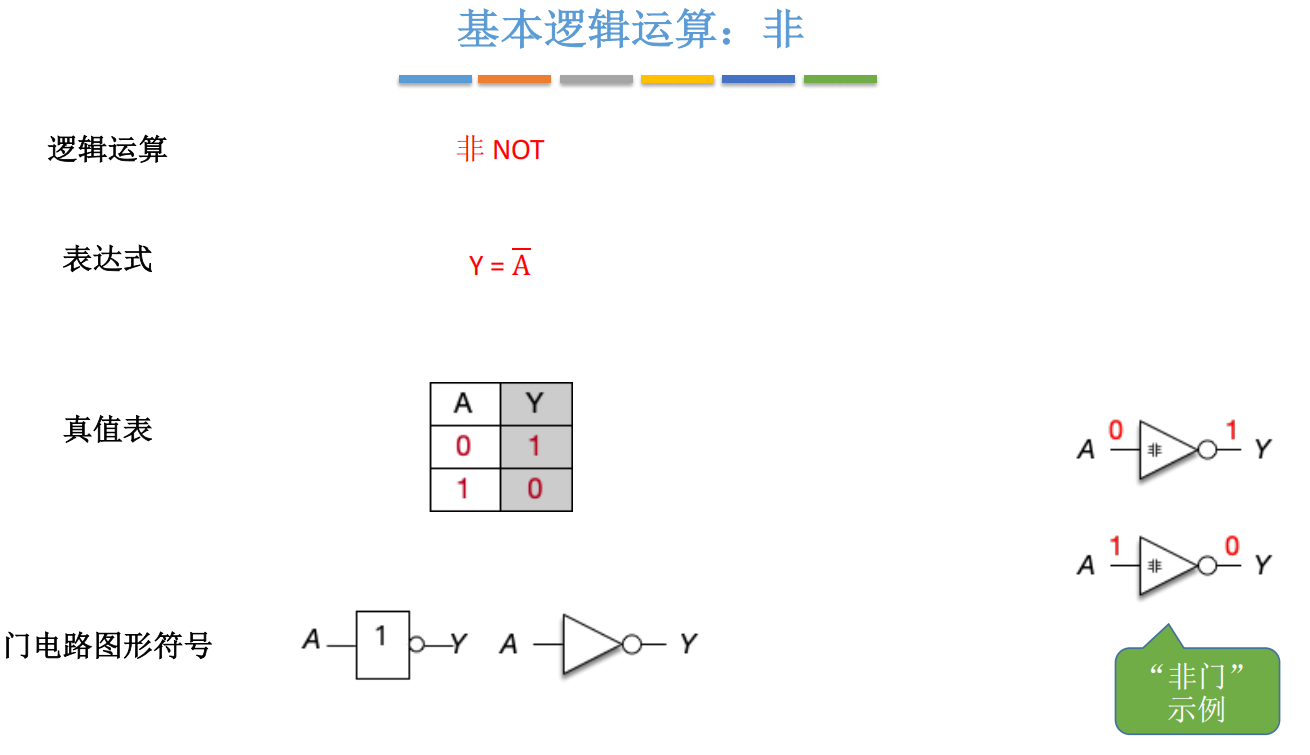
``
图示说明:非门由一个放大器符号(三角形)加输出端小圆圈构成。小圆圈 = "取反"标志,是所有"非"操作的视觉锚点。
博主提示 :
在考试中,经常要求你根据符号判断门类型。记住三句话:
- 输入直线 → 与门
- 输入弧线 → 或门
- 有小圆圈 → 带"非"操作
三、复合逻辑门
有了 AND、OR、NOT,我们就能搭出更复杂的逻辑。
3.1 与非门(NAND)
表达式为y=ā·b,先与后⾮
逻辑表达式 :
Y = A ⋅ B ‾ Y = \overline{A \cdot B} Y=A⋅B
实现方式 :AND + NOT
简化符号:与门 + 输出小圆圈
真值表(与 AND 完全相反):
| A | B | Y = A B ‾ \overline{AB} AB |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
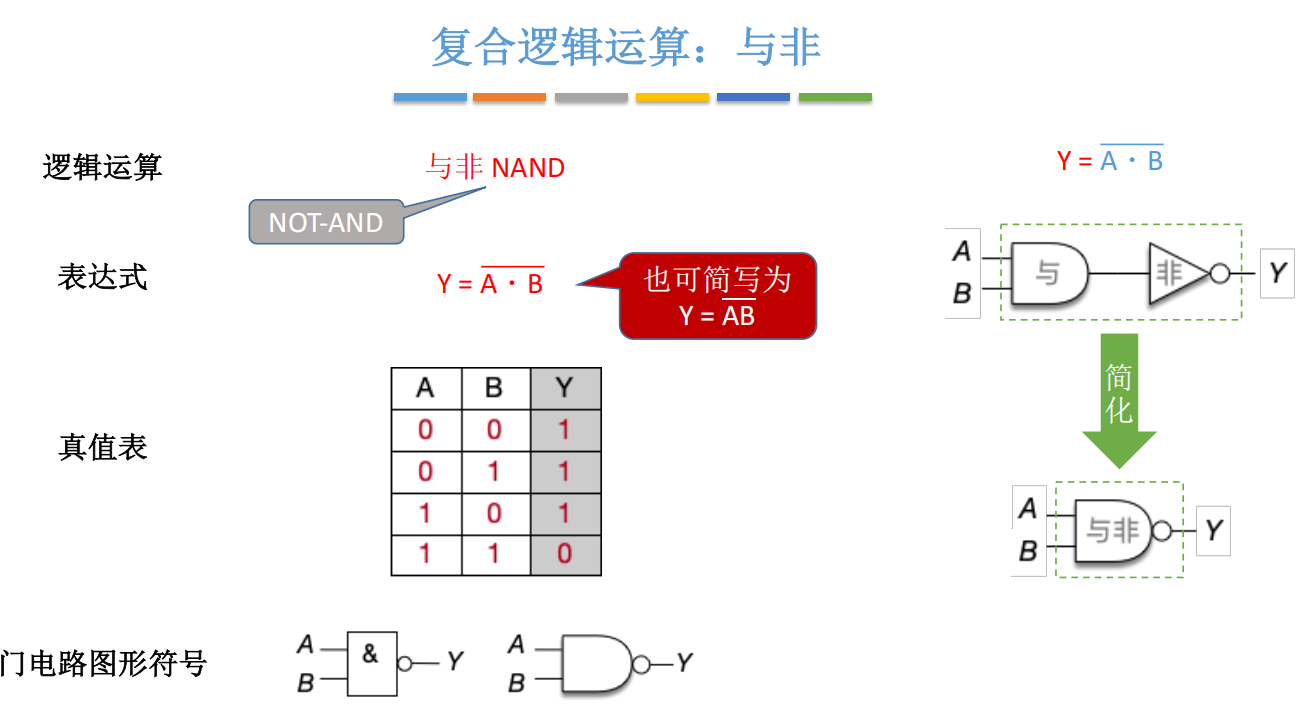 |
神奇事实 :仅用 NAND 门,就能构建任何逻辑电路! (包括 CPU!)
这就是为什么 NAND 是芯片制造中最基础的单元之一。
3.2 或非门(NOR)
表达式为y=a+b,先或后⾮
逻辑表达式 :
Y = A + B ‾ Y = \overline{A + B} Y=A+B
实现方式 :OR + NOT
简化符号:或门 + 输出小圆圈
真值表:
| A | B | Y = A + B ‾ \overline{A+B} A+B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
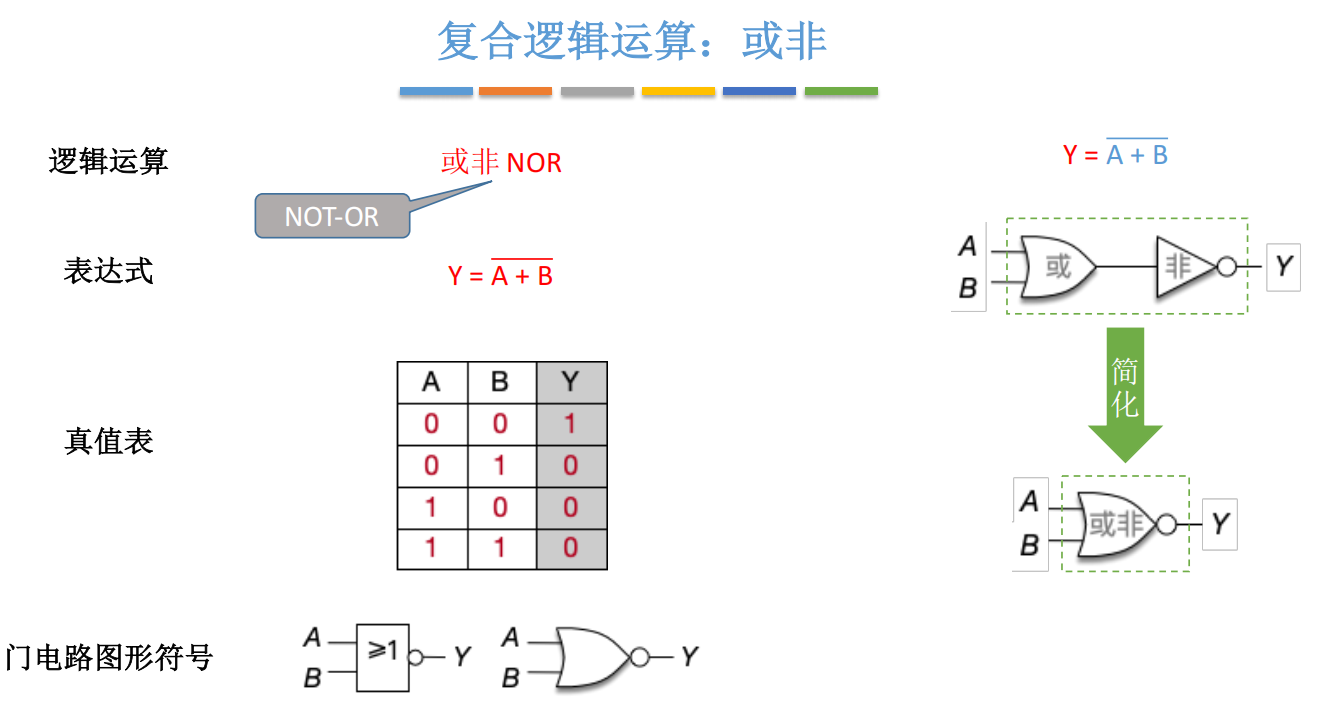 |
规则 :只有 A 和 B 都为 0,输出才是 1。
3.3 异或门(XOR)
表达式为y=a⊕b,输⼊相异时输出1
逻辑表达式 :
Y = A ⊕ B Y = A \oplus B Y=A⊕B
运算规则:
- A ≠ B → Y = 1
- A = B → Y = 0
真值表:
| A | B | Y = A⊕B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
如何用基本门实现 XOR?
核心思想:"A=0,B=1" 或 "A=1,B=0"
Y = ( A ‾ ⋅ B ) + ( A ⋅ B ‾ ) Y = (\overline{A} \cdot B) + (A \cdot \overline{B}) Y=(A⋅B)+(A⋅B)
电路实现:
- 用两个 NOT 门得到 A ‾ \overline{A} A 和 B ‾ \overline{B} B
- 用两个 AND 门计算 A ‾ B \overline{A}B AB 和 A B ‾ A\overline{B} AB
- 用一个 OR 门合并结果
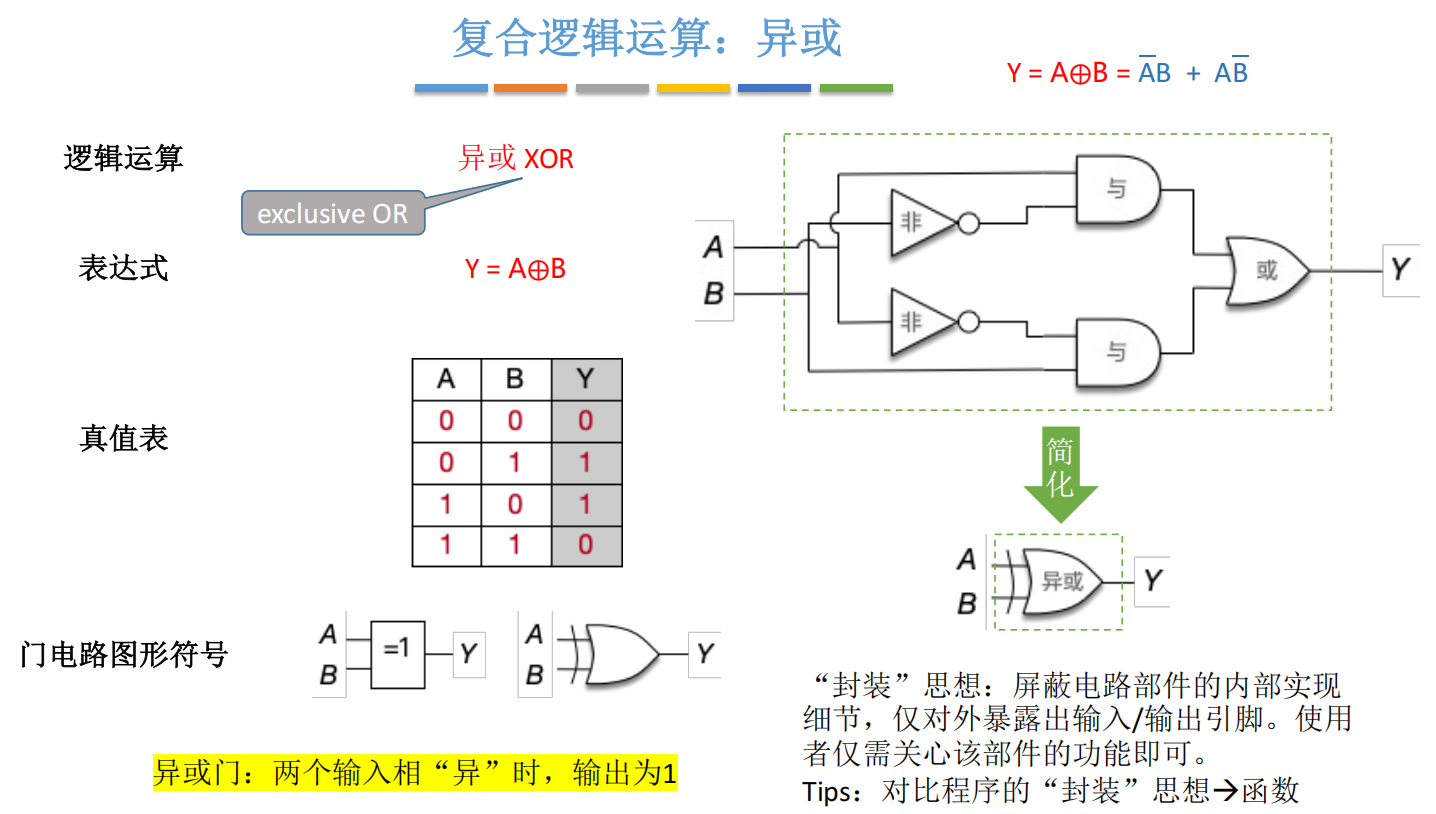
``
图示说明 :上侧展示由 2 个 NOT、2 个 AND、1 个 OR 构成的完整 XOR 电路;下侧为封装后的 XOR 门符号------或门输入端加一层"双眼皮"弧线,极具辨识度。
多比特异或的奇偶特性
对 n n n 个比特进行连续异或:
Y = b 1 ⊕ b 2 ⊕ ⋯ ⊕ b n Y = b_1 \oplus b_2 \oplus \cdots \oplus b_n Y=b1⊕b2⊕⋯⊕bn
- 若 1 的个数为奇数 → Y = 1 Y = 1 Y=1
- 若 1 的个数为偶数 → Y = 0 Y = 0 Y=0
应用:
- 奇偶校验:检测数据传输错误
- 二进制加法:半加器的核心(不考虑进位时,和 = A ⊕ B)
验证:
c// 4 个 1(偶数)→ 结果为 0 int r1 = 1 ^ 0 ^ 0 ^ 1 ^ 1 ^ 0 ^ 1; // = 0 // 5 个 1(奇数)→ 结果为 1 int r2 = 1 ^ 0 ^ 1 ^ 0 ^ 1 ^ 1 ^ 1; // = 1
3.4 同或门(XNOR)
同或运算(NOR)是异或运算的逆运算,其符号为⼀个圆圈中间加⼀个点。实现同或运算的逻辑⻔电路需在异或⻔输出端接⼀个⾮⻔,封装后图形表现为异或⻔输出端加⼩圆圈。
同或⻔与异或⻔逻辑相反:当输⼊值相同时输出为1,相异时输出为0。部分教材将同或⻔称为异或非门,但主流仍采⽤同或门命名。
逻辑表达式 :
Y = A ⊙ B = A ⊕ B ‾ Y = A \odot B = \overline{A \oplus B} Y=A⊙B=A⊕B
规则:A = B → Y = 1;A ≠ B → Y = 0
实现方式 :XOR + NOT
符号 :XOR 门 + 输出小圆圈
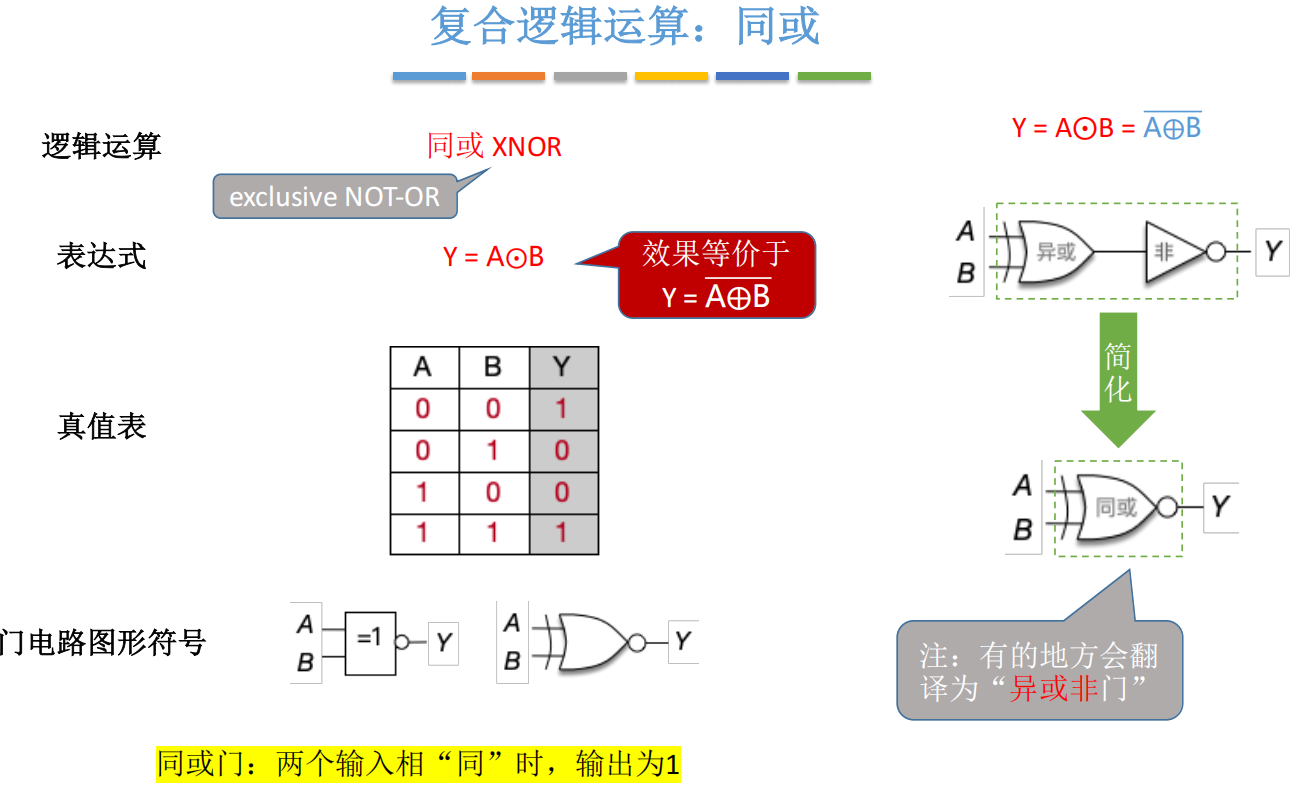
💬 别名:也叫"异或非门",但主流教材称"同或"。
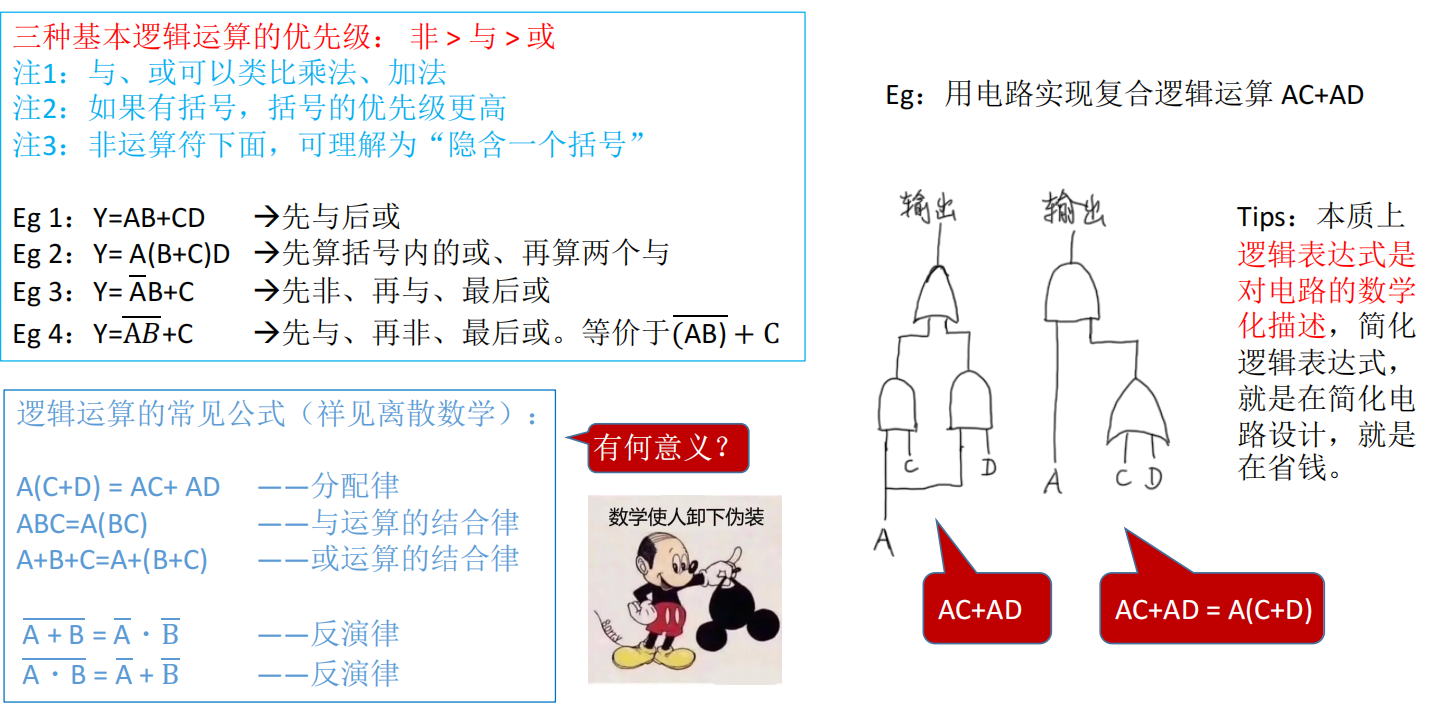
四、逻辑表达式的优先级与化简
4.1 运算优先级
非(NOT) > 与(AND) > 或(OR) \text{非(NOT)} > \text{与(AND)} > \text{或(OR)} 非(NOT)>与(AND)>或(OR)
类比算术:非 ≈ 幂,与 ≈ 乘,或 ≈ 加
示例分析:
c
// 逻辑表达式:Y = A·B + C·D
// 先算 A·B 和 C·D(与),再或
c
// Y = A·(B + C)·D
// 括号优先:先算 B+C,再与 A、D 相与
c
// Y = \overline{A·B} + C
// 先算 A·B,再取非,最后 + C踩坑指南 :
当非运算的横线覆盖多个变量(如 A B ‾ \overline{AB} AB),相当于对整个子表达式取反 ,等价于 ( A ⋅ B ) ‾ \overline{(A \cdot B)} (A⋅B)。不要误以为只对 B 取反!
4.2 逻辑公式
(1)分配律(节省门电路!)
A ⋅ ( C + D ) = A ⋅ C + A ⋅ D A \cdot (C + D) = A \cdot C + A \cdot D A⋅(C+D)=A⋅C+A⋅D
电路优化案例:
- 原始设计:需要 2 个 AND + 1 个 OR
- 优化后:1 个 OR + 1 个 AND
省下一个 AND 门 = 省下成千上万个晶体管 = 省下百万美元制造成本!
(2)结合律
A ⋅ B ⋅ C = ( A ⋅ B ) ⋅ C = A ⋅ ( B ⋅ C ) A \cdot B \cdot C = (A \cdot B) \cdot C = A \cdot (B \cdot C) A⋅B⋅C=(A⋅B)⋅C=A⋅(B⋅C)
A + B + C = ( A + B ) + C = A + ( B + C ) A + B + C = (A + B) + C = A + (B + C) A+B+C=(A+B)+C=A+(B+C)
(3)德摩根律(De Morgan's Laws)
A ⋅ B ‾ = A ‾ + B ‾ \overline{A \cdot B} = \overline{A} + \overline{B} A⋅B=A+B
A + B ‾ = A ‾ ⋅ B ‾ \overline{A + B} = \overline{A} \cdot \overline{B} A+B=A⋅B
口诀 :"打破横线,符号翻转"
应用:将 NAND 转换为 OR+NOT,便于电路布局。
高频考点 :
"如何用 NAND 门实现 NOT、AND、OR?"
答案:
- NOT A = NAND(A, A)
- A AND B = NOT(NAND(A, B)) = NAND(NAND(A,B), NAND(A,B))
- A OR B = NAND(NOT A, NOT B) = NAND(NAND(A,A), NAND(B,B))
五、从门电路到芯片
5.1 门电路如何实现?
每个逻辑门,最终都由晶体管(Transistor)构成。例如:
- CMOS 与非门:用 2 个 PMOS + 2 个 NMOS 晶体管
- CMOS 或非门:用 2 个 PMOS + 2 个 NMOS(不同连接方式)
5.2 芯片制程:
- 芯片制程 (如 10nm、7nm、3nm):指晶体管栅极宽度
- 人类头发直径 ≈ 0.1 mm = 100,000 纳米
- 10nm 晶体管宽度 = 头发丝的 1/10,000
现实意义:
- 制程越小 → 晶体管越小 → 单位面积晶体管越多
- 苹果 M3 芯片:200 亿个晶体管集成在指甲盖大小的硅片上!
5.3 光刻机:
- EUV 光刻机(Extreme Ultraviolet):使用 13.5nm 波长的极紫外光
- 全球唯一供应商:荷兰 ASML 公司
- 一台 EUV 光刻机重达 180 吨,售价超 1.5 亿美元

结语:
逻辑门看似简单,却是整个数字世界的基石。从 if 判断到 AI 大模型,背后都是 AND、OR、NOT 的无限组合。
本篇文章是为了帮助大家温习一下数字电路的相关知识,帮助大家更好的理解,所以数字电路基础的知识点会占据几篇的篇幅。