一、矩阵的初等变换
1、背景引入

2、三种初等变换
(1)交换:
①交换两行:
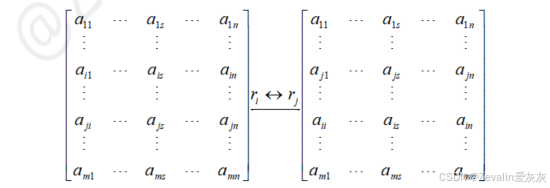
②交换两列:
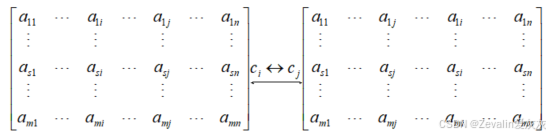
(2)数乘:
①某行乘以系数:
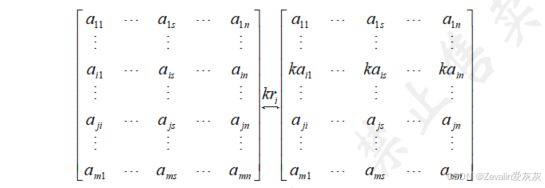
②某列乘以系数:
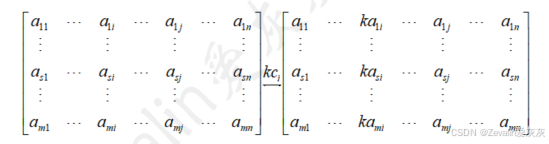
(3)倍加变换:
①某行的k倍加到另外一行:
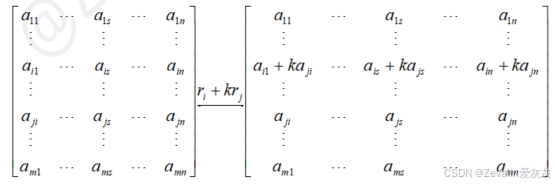
②某列的k倍加到另外一列:
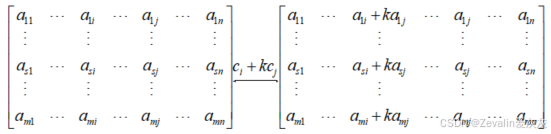
3、初等矩阵
(1)将单位矩阵做一次且仅做一次初等变换(对同序号的行或列做同样的初等变换,结果是一致的,故不区分行/列)得到的矩阵称为初等矩阵。

(2)初等矩阵的意义为,在任一矩阵左边乘以一个初等矩阵,相当于对其进行了一次一样的初等行变换,而在任一矩阵右边乘以一个初等矩阵,相当于对其进行了一次一样的初等列变换。

(3)初等矩阵求逆公式:

4、利用初等变换求逆矩阵
(1)初等变换的性质:

(2)数字型逆矩阵的求法:

5、矩阵的等价

6、例题


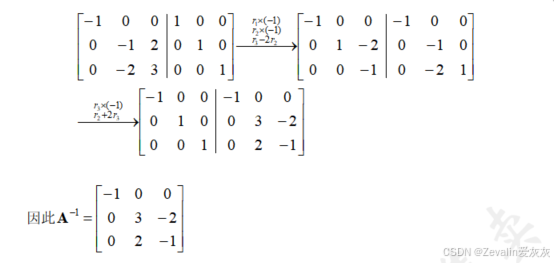


二、矩阵的秩
1、k阶子式

2、矩阵的秩的定义

3、矩阵的秩的性质

4、两类特殊矩阵
(1)行阶梯型矩阵:矩阵中每一行的非0首元素所在列比下一行的非0首元素所在的列都靠前(并排不算)。
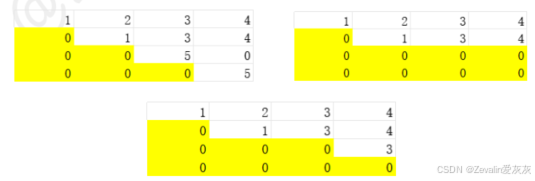
(2)行最简型矩阵:矩阵中每一行的非0首元素为1,且非0首元素所在列的其它元素为0。

5、例题



三、线性方程组解的存在性
1、非齐次线性方程组与齐次线性方程组回顾
(1)任意一个n元非齐次线性方程组均可表示为
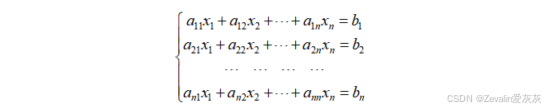

(2)任意一个n元齐次线性方程组均可表示为
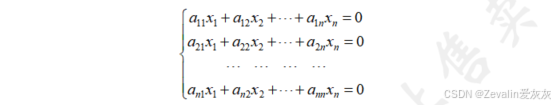

2、解的存在性


3、举例



