论文题目：SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS（基于图卷积网络的半监督分类）
会议：ICLR2017
摘要：我们提出了一种可扩展的方法，用于图结构数据的半监督学习，该方法基于直接在图上操作的卷积神经网络的有效变体。我们通过谱图卷积的局部一阶近似来激励卷积架构的选择。我们的模型在图边的数量上线性扩展，并学习编码局部图结构和节点特征的隐藏层表示。在引文网络和知识图谱数据集的大量实验中，我们证明了我们的方法在很大程度上优于相关方法。
深入理解图卷积网络（GCN）
引言
图神经网络（Graph Neural Networks）正在成为处理非欧几里得数据的重要工具。今天我们来详细解读Thomas Kipf和Max Welling于ICLR 2017发表的经典论文《Semi-Supervised Classification with Graph Convolutional Networks》。这篇论文提出的GCN模型已成为图学习领域的基础架构。
问题定义
考虑这样一个场景：我们有一个引用网络，其中文档是节点，引用关系是边，每个文档有词袋特征向量。我们只知道少量文档的类别标签（例如每类只有20个），但可以访问所有文档的特征和整个图结构。如何有效利用图结构来改善分类性能？
传统的图半监督学习方法使用以下损失函数：
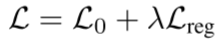
其中正则化项为：
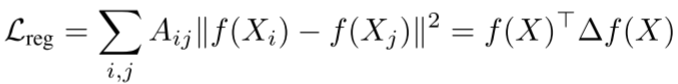
这个正则化项强制相连节点的表示相似，但这一假设过于简化了图边的含义。
GCN的核心创新
1. 从谱图理论到简化卷积
GCN的理论基础源于谱图卷积。在图的傅里叶域中，卷积操作定义为：
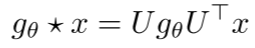
其中U是归一化图拉普拉斯矩阵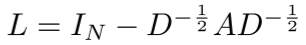
的特征向量矩阵。
然而，这种方法有两个问题：
- 计算复杂度高（O(N^2)）
- 需要计算图拉普拉斯的特征分解
为解决这些问题，论文采用了以下简化策略：
第一步：使用切比雪夫多项式近似（Chebyshev approximation）：
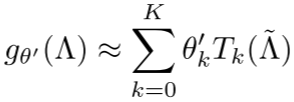
第二步：限制为一阶近似（K=1），假设最大特征值λ≈2：
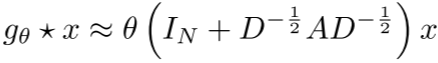
第三步：重归一化技巧，避免数值不稳定：
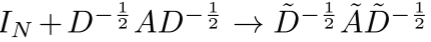
其中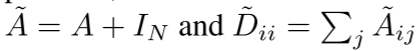
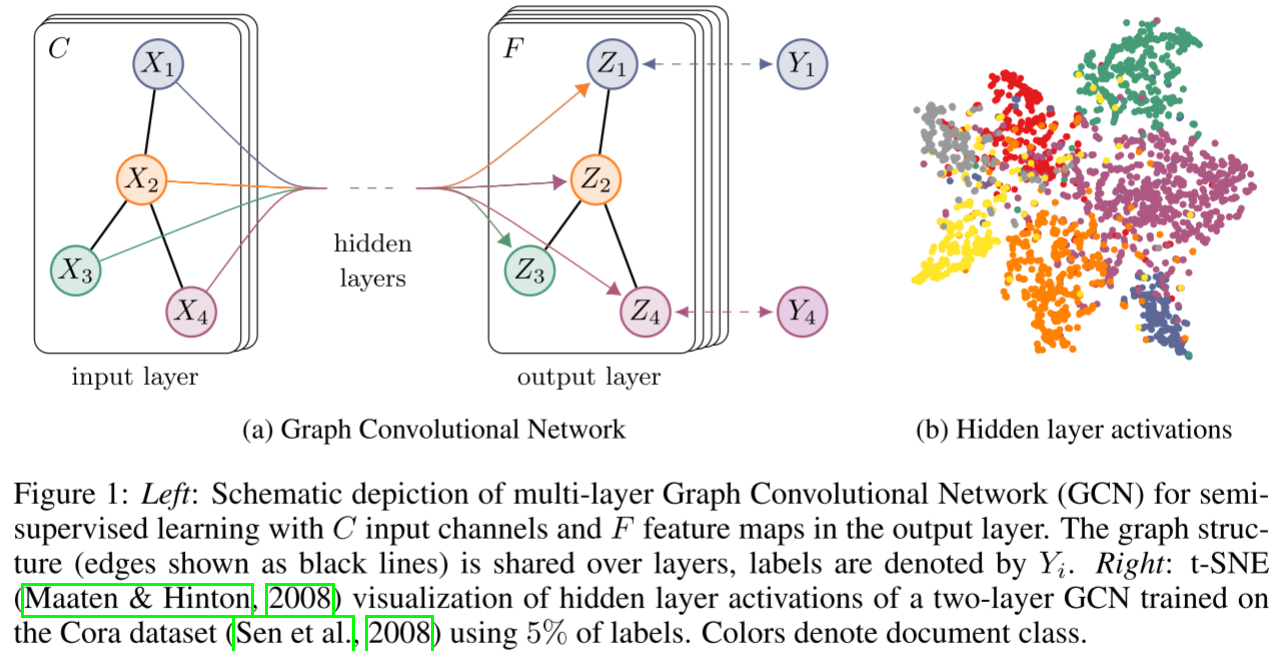
2. 多层GCN架构
对于半监督节点分类，论文使用两层GCN：
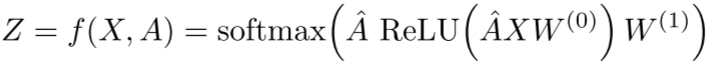
损失函数为标记节点的交叉熵：
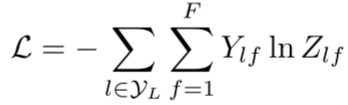
实验验证
数据集统计：
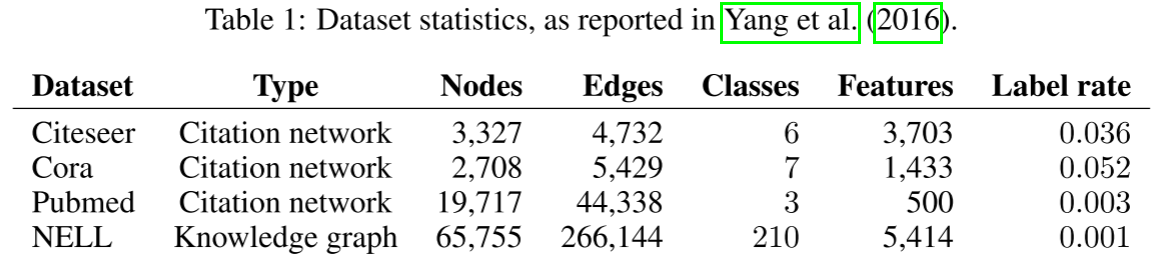
- Cora: 2,708个节点，5,429条边，7个类别，1,433维特征
- Citeseer: 3,327个节点，4,732条边，6个类别，3,703维特征
- Pubmed: 19,717个节点，44,338条边，3个类别，500维特征
训练设置：
- 每类仅使用20个标记样本训练
- 使用500个节点验证
- 1000个节点测试
- 优化器：Adam（学习率0.01）
- 正则化：Dropout (0.5) + L2正则化 (5 \\times 10\^{-4})
- 早停策略：验证损失10个epoch不下降则停止
性能对比：
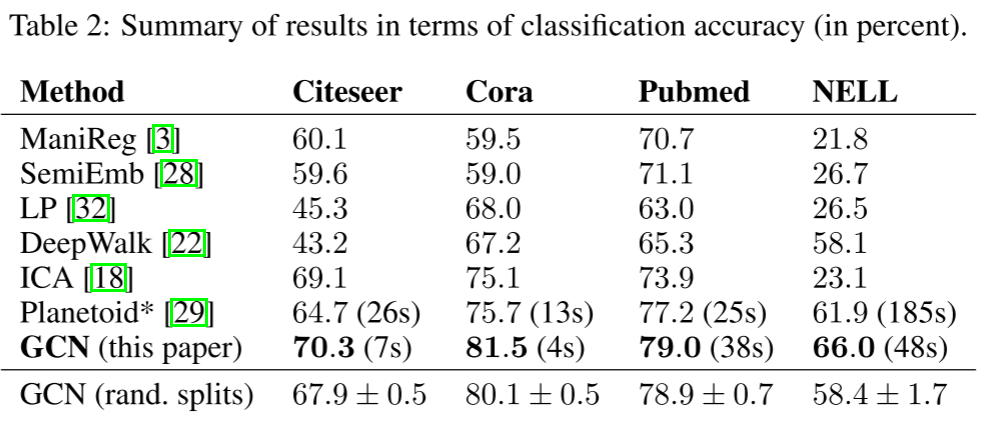
GCN在所有三个数据集上都达到了最佳或接近最佳的性能。
传播模型消融实验（Cora数据集）：
- 3阶Chebyshev滤波器：79.5%
- 一阶模型（两个参数）：80.0%
- 单参数模型：79.2%
- 重归一化技巧 ：81.5%
- 仅一阶项：80.5%
- MLP（无图结构）：55.1%
可以看到重归一化技巧带来了关键的性能提升。
训练效率： 在随机图上的训练时间（每个epoch，GPU）：
- 1k边：~0.001秒
- 10k边：~0.01秒
- 100k边：~0.1秒
- 1M边：~1秒
时间复杂度确实与边数呈线性关系。
模型深度分析
论文附录中还研究了模型深度的影响。在5折交叉验证实验中发现：
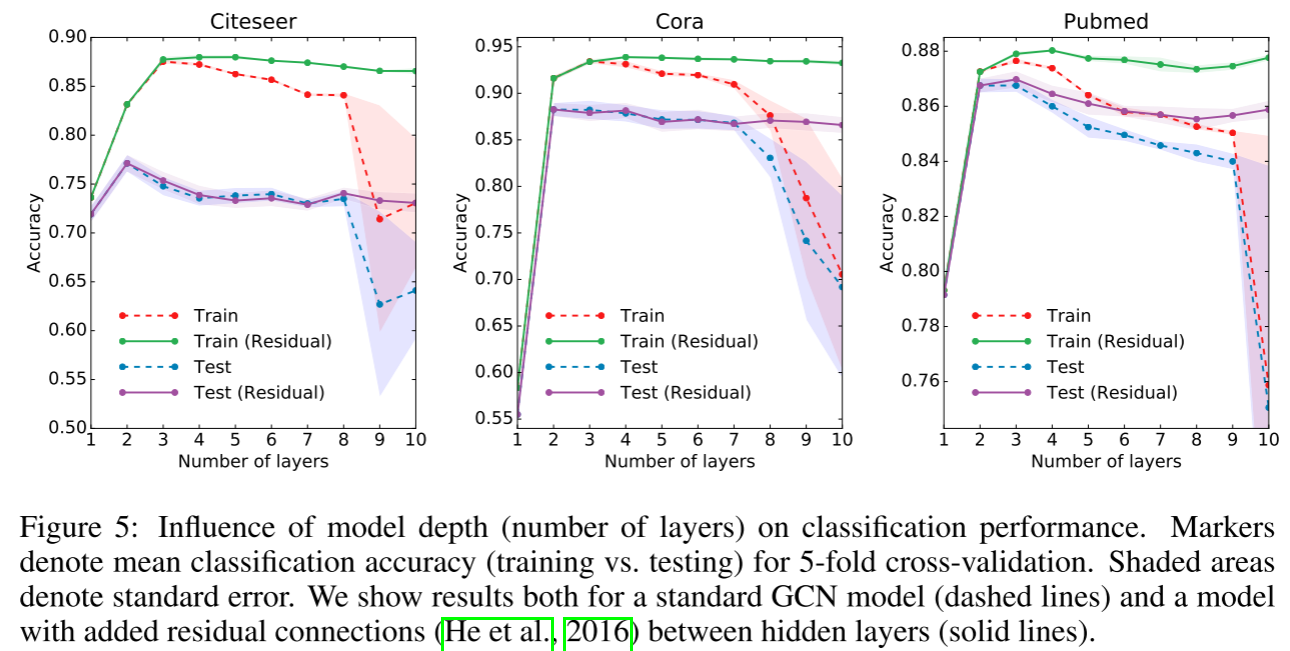
- 2-3层模型效果最好
- 超过7层，训练变得困难（过拟合和梯度问题）
- 残差连接可以帮助训练更深的模型
局限性与未来方向
论文诚实地讨论了几个局限：
-
内存需求：当前使用全批次梯度下降，内存随数据集大小线性增长。可以通过mini-batch训练改进。
-
有向图和边特征：当前框架不直接支持。可以通过二部图表示来处理。
-
假设的局限性：隐式假设了局部性（K层GCN依赖K阶邻域）和自连接与邻居边的等重要性。
总结
GCN通过巧妙的理论简化和工程设计，提出了一个简单而强大的图神经网络架构。其核心贡献包括：
- 从谱图理论出发，推导出简单高效的传播规则
- 实现了线性时间复杂度（相对于边数）
- 在多个基准数据集上取得了SOTA性能
- 为后续大量图神经网络研究奠定了基础
这篇论文的引用量已超过数万次，充分证明了其在图学习领域的重要地位。如果你对图神经网络感兴趣，GCN绝对是必读的经典论文。