1. 引言
2018年一个严重的蓝牙漏洞引起了广泛关注。这是 Biham 和 Newman 的一项精彩发现。鉴于 BLE(Bluetooth Low Energy,低功耗蓝牙) 在"很少打补丁"的物联网世界中的广泛使用,该漏洞具有非常严重的影响。然而,这个漏洞在概念上却异常干净、简单。不同于许多椭圆曲线漏洞,普通人完全可以理解这个漏洞及其利用方式。这是一个在概念上相当容易理解的攻击的绝佳应用。
本文将介绍这个漏洞本身、如何对其进行利用,以及它是如何具体出现在蓝牙协议中的。但在此之前,先快速了解一下椭圆曲线和无效曲线点攻击。
2. 何为椭圆曲线?
这个名字其实相当具有误导性。在密码学中,"椭圆曲线"既不是椭圆形的,也不是连续的曲线。相反,它是一组 ( x , y ) (x, y) (x,y) 坐标点,其中 x x x 和 y y y 的取值范围在 0 0 0 到 p p p 之间, p p p 是一个素数,并且满足:
y 2 = x 3 + a x + b ( m o d p ) y^2 = x^3 + ax + b \pmod p y2=x3+ax+b(modp)
此外,还有一个额外的"无穷远点",它的行为在直觉上很像 0 0 0:
- 把它加到任何点上,结果还是原来的点。
图 1 展示了这样一条曲线,其中 y 2 = x 3 − x y^2 = x^3 - x y2=x3−x,而 x x x 和 y y y 的取值范围是 0 0 0 到 71 71 71。(严格来说, x x x 和 y y y 是定义在有限域上的,但当 p p p 是素数时,所有阶为 p p p 的有限域彼此同构(isomorphic),因此本定义是等价的。)
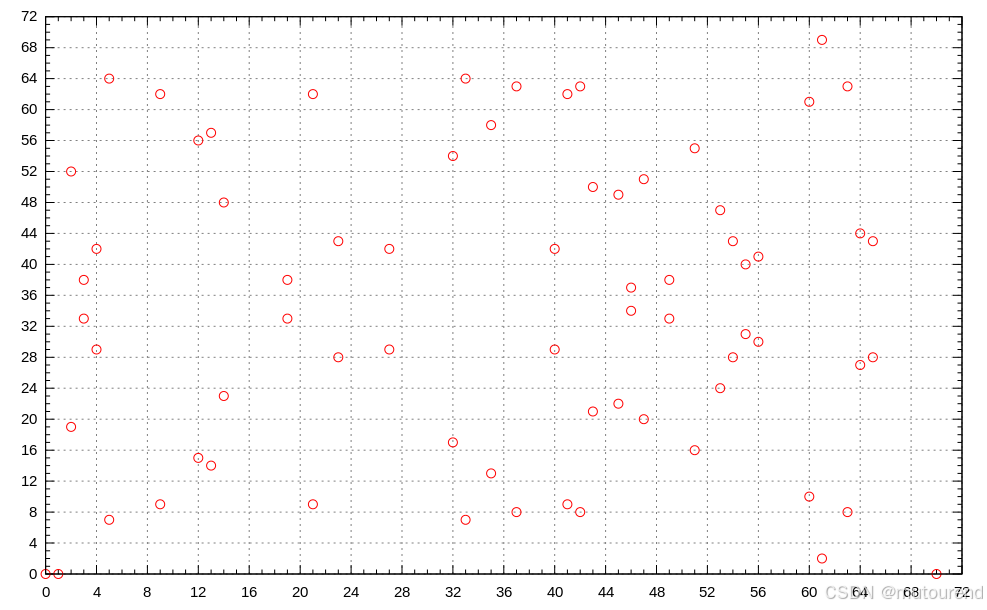
图 1:椭圆曲线(密码学中使用的形式)
椭圆曲线具有一些非常有用的性质:
- 可以将椭圆曲线上的点相加,其规则看起来很像普通加法: x + y = y + x x + y = y + x x+y=y+x, x + ( y + z ) = ( x + y ) + z x + (y + z) = (x + y) + z x+(y+z)=(x+y)+z,等等。这是因为曲线上的点构成了一个阿贝尔群。可以在下方的图 2 中看到这种加法的可视化表示。
- 一个点可以通过"加自身 n n n 次"的方式,与某个自然数(记为 n n n)相乘。
- 对于每一个点 ( x , y ) (x, y) (x,y),都存在一个逆元 ( x , − y ) (x, -y) (x,−y),使得该点与其逆元相加得到无穷远点。
- 最重要的是,如果在上面的方程中恰当地选择 a a a、 b b b 和 n n n,那么"乘以一个普通数"就构成了一个trapdoor 陷门函数:
- 给定一个点 P P P 和一个数 n n n,计算出满足 Q = n ∗ P Q = n * P Q=n∗P 的点 Q Q Q 非常容易;但反过来,给定点 P P P 和点 Q Q Q,要找到满足 Q = n ∗ P Q = n * P Q=n∗P 的 n n n 却极其困难。正是这一简单的困难性假设,使得能够构建大量的密码学算法。

图 2:点的加法与无穷远点(注意:这些插图为了便于理解使用了连续曲线,但这并不是实际使用的对象)
通常,椭圆曲线算法都是围绕某一条特定的曲线来编写的。通信双方交换曲线上的点和标量,并使用上面定义的运算规则进行计算。然而,当这些算法接收到不满足曲线方程的 ((x, y)) 坐标对时,就会产生问题,而这正是所谓的"无效曲线点攻击(invalid curve point attack)"得以利用的根源。
3. 何为无效曲线点攻击(Invalid Curve Point Attack)?
回顾一下,所谓"点",是指一对 ( x , y ) (x, y) (x,y),满足对某些 a a a、 b b b、 p p p 有
y 2 = x 3 + a x + b ( m o d p ) y^2 = x^3 + ax + b \pmod p y2=x3+ax+b(modp)。
如果该等式不成立,那么 ( x , y ) (x, y) (x,y) 就是一个无效的曲线点(invalid curve point)。
相当多的密码学算法会要求用户提供一个曲线点,并在设计上假设该点是有效的 、即默认曲线方程成立。如果在对接收到的曲线点进行数学运算之前,没有先验证它是否确实在曲线上,这种做法几乎等同于违反了加密学末日原则(cryptographic doom principle),并且会带来类似的严重后果。
在椭圆曲线密码体制中,秘密通常是一个普通的数(如 已知 P P P 和 Q = n ∗ P Q = n * P Q=n∗P,求 n n n 是困难问题)。如果攻击者能够发送一个未经验证的点 ,让系统用秘密值 n n n 去乘它,并且攻击者能观察结果,那么就可以利用这种缺乏验证的漏洞来推断出秘密密钥。通常,攻击者可以选择属于另一条曲线的点,而不是算法所指定的那条曲线,并且那条曲线上的点数可能非常少。
如,攻击者可以选择一个不在曲线上 、且 y 坐标为 0 的点。任何这样的点,在与自身相加时,结果必然是无穷远点。原因是:
- 计算逆元时,会对 y 坐标取负数,而 0 乘以 −1 仍然是 0,因此任何 y 坐标为 0 的点都是它自己的逆元。于是,该点与自身相加的结果必然是无穷远点。
如果攻击者选择了这样的点,那么只要观察"秘密值乘以该点"的结果,就可以判断秘密是奇数还是偶数!输入的点只有两种可能的结果:
- 如果秘密是奇数,结果就是该点本身;
- 如果秘密是偶数,结果就是无穷远点。
同理,还可以提交一些点,使得它们在乘以 3 3 3 时等于无穷远点,从而得到秘密 m o d 3 \mod 3 mod3;乘以 5 时等于无穷远点,从而得到秘密 m o d 5 \mod 5 mod5;依此类推。最终,可以使用中国剩余定理(Chinese Remainder Theorem)来计算出真正的秘密值。
这并不是利用无效曲线点泄露密钥的唯一方式,但它可能是最容易理解的一种 ,而且已经在现实中被用来攻破来自 Oracle 和 Google 的 TLS 库。
最近针对 Bluetooth 的攻击虽然不完全像上面的例子那样简单,但在概念上非常相似,同样利用了**小子群限制(small subgroup confinement)**技术来实现密钥泄露。
4. Bluetooth 攻击原理
Bluetooth 协议使用椭圆曲线 Diffie--Hellman(ECDH) 来协商用于加密的共享密钥。正确地使用 Diffie--Hellman 算法是非常困难的,一些看似细微的错误就足以破坏整个系统的安全性。
本案例中的协议实际上要求进行曲线点验证 ,但只验证了 x 坐标。这是一个看起来无伤大雅、却足以在十年间未被发现的错误。而它恰恰让聪明的攻击者能够彻底攻破整个系统。
椭圆曲线 Diffie--Hellman 算法本身非常简单。假设 Alice 和 Bob 想要协商一个秘密值。双方各自拥有一个秘密数,并且事先约定了一条椭圆曲线上的"基点"。
Alice 将基点乘以她的秘密数后发送给 Bob,Bob 也将基点乘以他的秘密数后发送给 Alice。随后,Alice 用自己的秘密数去乘 Bob 发来的点,而 Bob 用自己的秘密数去乘 Alice 发来的点。
如果将基点记为 P P P,秘密记为 a a a 和 b b b,那么:
- Alice 发送给 Bob: a ∗ P a * P a∗P
- Bob 发送给 Alice: b ∗ P b * P b∗P
- Alice 计算: a ∗ ( b ∗ P ) a * (b * P) a∗(b∗P)(共享秘密)
- Bob 计算: b ∗ ( a ∗ P ) b * (a * P) b∗(a∗P)(同一个共享秘密)
即使攻击者 Chuck 能看到这些消息,他也无法推导出 a a a 或 b b b,也无法将 a ∗ P a * P a∗P 和 b ∗ P b * P b∗P 组合出共享秘密,因此看起来毫无办法。
然而,当 Chuck 不只是被动监听 ,而是能够篡改消息时,问题就出现了。由于 y 坐标没有被验证,Chuck 可以将其修改为恒等于 0。
回忆一下:如果一个点的 y 坐标为 0,那么将它乘以一个随机数时,有 50% 的概率得到无穷远点 ,50% 的概率得到原始点,而不可能得到其他结果。
综合来看,如果 Chuck 将 Alice 和 Bob 之间传递的点 ( x , y ) (x, y) (x,y) 替换为 ( x , 0 ) (x, 0) (x,0),那么当 Alice 或 Bob 用自己的私钥去乘这个点时,就有 50% 的概率得到无穷远点,50% 的概率得到 ( x , 0 ) (x, 0) (x,0)。
如果 Chuck 替换了两个中间消息 ,那么 Alice 和 Bob 有 25% 的概率 会一致认为共享密钥是无穷远点,而且不可能在其他值上达成一致。
这意味着:
- 要么 ECDH 协议失败,Alice 和 Bob 需要重试(给了 Chuck 再一次机会);
- 要么 Chuck 已经知道了共享密钥,从而能够读取并篡改通信内容。
5. 如何避免这类漏洞?
从整个事件中最重要的启示,并不是某一次具体攻击的细节,而是:这一整类攻击其实是完全可以避免的。下面是一些更具体的建议:
- Diffie-Hellman 是一种实现起来异常危险的算法。几乎可以肯定,自己并不应该直接使用它(参考 Latacora 的2018年4月博客《Cryptographic Right Answers》)。若发现有人在使用它,那么很有可能还能发现其他漏洞。说真的,几乎没有人真正需要自己实现它,而要把它正确实现又极其困难。
- 对于 ECDH,使用 X25519;对于 ECDSA,使用 Ed25519。在这些曲线上,任何 32 字节的字符串都是一个合法的曲线点,因此从根本上杜绝了无效曲线点攻击。
- 如果输入有可能是无效的,而又要对其执行密码学运算,那么在做任何运算之前,必须先进行校验。
关于"如何自行校验曲线点",可参看2003年论文《Validation of Elliptic Curve Public Keys》。
关于如何亲手练习利用这类漏洞(以及一些更酷的漏洞),可参看 Crypto Challenge Set 8。
参考资料
1\] The Trail of Bits 2018年8月博客 [You could have invented that Bluetooth attack](https://blog.trailofbits.com/2018/08/01/bluetooth-invalid-curve-points/)