密码学末日原则（The Cryptographic Doom Principle）

1. 引言

在设计安全协议时，有一个原则，大致可以表述为：

这是一个最著名的例子，展示了在验证 MAC 之前执行密码学操作是如何出问题的。一般来说，将消息认证码（MAC）与加密消息结合，有三种方式：

1）先认证再附加（Authenticate And Encrypt）：通常会严重失败。
发送方对明文计算 MAC，加密明文，然后将 MAC 追加到密文后面。
Ek1(P) || MACk2(P)
2）先认证后加密（Authenticate Then Encrypt）：在多数情况下可用。
发送方对明文计算 MAC，然后将明文和 MAC 一起加密。
Ek1(P || MACk2(P))
3）先加密后认证（Encrypt Then Authenticate）：通常是最优的。
发送方先加密明文，然后对密文计算 MAC 并追加。
Ek1(P) || MACk2(Ek1(P))

第一种方式通常会严重失败，第二种方式在多数情况下可用，而第三种方式通常是最优的。

第三种"先加密后认证"是最优的，因为它不违反末日原则：

相比之下，"先认证后加密"虽然乍看之下可行，但它确实违反了末日原则。因为要验证 MAC，接收方必须先解密消息------因为 MAC 本身是加密负载的一部分。许多协议设计者（包括 SSL 的设计者）并未认为这是个问题，于是他们选择去验证"末日是否真的不可避免"。

在 CBC 模式下解密密文时，解密过程的一部分是移除最初为使明文长度满足分组大小而添加的填充（padding）。填充格式有多种，但最常见的一种（由 PKCS#5 定义）是：追加 N 个字节，每个字节的值都等于 N。

如，如果需要填充 5 个字节，就追加 5 个值为 0x05 的字节。

接收消息时，接收方会先解密，然后查看最后一个字节的值（记为 N），并确保前面的 N−1 个字节也都是值 N。如果不满足，就判定为填充错误并中止。由于 MAC 是加密负载的一部分，所有这些操作都必须在验证 MAC 之前完成。于是，末日降临。

回顾下CBC 的解密过程如下：

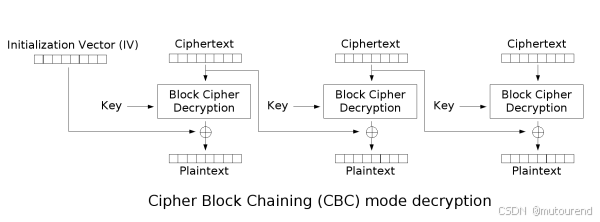
如果攻击者持有一条他们想要解密的密文消息，只需在发送给接收方之前，随意修改倒数第二个密文块的最后一个字节，就会对最后一个密文块的最后一个字节产生确定性的影响。而正是这个字节会被接收方用来处理填充。

因此，接收方在处理消息时，会遇到两种与密码相关的错误条件：

有时协议会针对不同错误返回不同的响应；即使没有，攻击者通常也能通过时间差来区分这两种情况。

这意味着，如果攻击者随意修改倒数第二个块的最后一个字节（上文提到的 R），大概率会触发填充错误。因为修改会影响最后一个块的最后一个字节，而接收方正是依赖该字节来判断填充。如，原本应该是 5 个 0x05，结果变成了 4 个 0x05 加上一个随机值。

如果攻击者对 R 尝试足够多次不同的修改（而它只有 8 比特空间），最终就会触发 MAC 错误 ，而不是填充错误。这是因为最后一个字节最终会被设置为 0x01，而这是一个合法的填充值。

此时，攻击者就知道：最后一个密文块的真实最后一个字节等于 R xor 1。

攻击者成功解密了一个字节！

接下来，他们可以有目的地将最后一个字节设为 0x02，并对倒数第二个块的倒数第二个字节重复同样的过程。如此反复，直到恢复整个消息。

末日降临。

下面这个针对 SSH 的明文恢复攻击是另一个对末日原则极其巧妙的利用。SSH 的数据包格式如下：

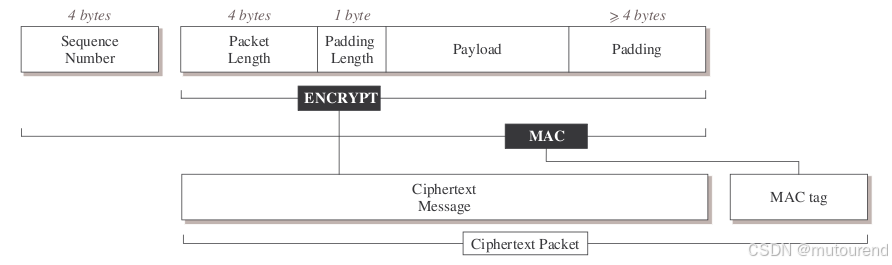
可以看到，SSH 和上面的情况有同样的问题：

乍一看，SSH 似乎是安全的，因为它使用的填充方式并不会像 Vaudenay 攻击那样暴露问题------它在负载之前的固定位置用一个字节指定填充长度，从而绕开了该问题。

然而，SSH 还有一个奇怪的特性：

这意味着，在验证 MAC 之前，接收方必须先解密消息的第一个分组。不仅是为了计算 MAC，更是为了知道消息的长度，以及需要从网络中读取多少数据来完成解密。

因此，在验证 MAC 之前，接收方第一件事 就是解密第一个分组，并将前四个字节解释为消息长度。略去一些细节，这意味着：

如果攻击者手中有一个他们想解密的密文块（比如来自之前传输消息的中间部分），他们只需把它发送给接收方。接收方会解密它，并将前四个字节解析为长度，然后从网络中读取对应数量的数据，直到验证 MAC。

攻击者随后可以一次发送一个字节，直到接收方遇到 MAC 错误并关闭连接。此时，攻击者就知道接收方将那四个字节解释成了什么长度，从而泄露了该密文块中的前四个明文字节。

末日再次降临。

以上只是两个示例，实际上这种问题还有很多其他变体。一定要警惕它------即使这些具体案例并不适用，这种通用模式也总会以某种方式引发问题。
它从不失手。

1\] 2011年12月博客 [The Cryptographic Doom Principle](https://moxie.org/2011/12/13/the-cryptographic-doom-principle.html)