1. 引言
前序博客:
Latacora团队2018年博客 crypto right answers 的初衷是作为一份易于使用的指南,帮助工程师在不必深入复杂细节的情况下,选择合适的密码学方案。随着后量子密码学(Post-Quantum Cryptography,PQC)逐渐从纯学术研究话题转变为实际工程中需要认真对待的密码学问题,Latacora团队认为是时候更新其密码学建议了。
推荐 PQC 的一个主要难点在于:
- 从历史上看,人们一直能够为经典密码学提供"更好的"答案------更快、更安全的哈希函数,更强的密码 KDF,更易用的原语......
- 这些改进在本质上具有相同的"形状":可以在现有设计中直接替换掉旧组件,用新的组件无缝升级系统。如,MD5 和 BLAKE3 在安全性上不可同日而语,但几乎可以直接用 BLAKE3 替换 MD5,在 API 基本不变的情况下获得显著更高的安全性。
有时,还会获得一些更安全的设计或特性,使原语更快或更易用,如内置 nonce、带 MAC 模式的哈希函数等。也会得到一些新的基础构件,比如 XOF(可扩展输出函数),但除非你是协议设计者,否则通常不会直接受到影响。此外,通常会把那些潜在危险的组件封装得较难被误用,从而在大多数情况下保证安全。
不幸的是,当把视角扩展到 PQC 时,事情就变得复杂得多了。
- 首先,并不是所有新方案都和旧方案具有相同的"形状";
- 其次,权衡取舍明显增多。
在经典密码学中,可以同时拥有快速、小尺寸、安全、易用的签名算法;而在 PQC 中,往往必须在这些属性之间做选择,得到某些好处的同时失去另一些。这意味着,需要更深入地讨论实际目标。最后,许多 PQC 系统------即便是一些看起来非常有前景的方案------后来也被证明是完全不安全的,这使得很难给出一个有把握、经得起时间考验的推荐。
2018 年的 密码学的正确答案(Cryptographic right answers) 建立在 Ptacek 和 Percival 更早工作的基础之上,其中一些建议在十多年后依然完全适用;而 PQC 的局势则要更加反复无常。
正因为这是一个完全不同的"怪兽",决定把这篇文章拆分开来。仍然希望为那些已经听过相关背景、只需要一份"速查表"的读者提供直接的推荐(如果是这种情况,可以直接跳到"正确答案"部分),但与旧版不同的是,这一次必须先铺垫更多背景说明。
2. 为什么是现在?
之所以频繁敲响警钟,是因为人们已经意识到:足以威胁当前密码算法的量子计算机,可能会在未来 20 年内出现。根据 Mosca 定理,这意味着现在就应该开始行动。这一判断促使包括美国在内的多个政府,通过立法要求提前规划向抗量子密码系统的迁移。
秘密信息往往具有很长的生命周期。如,政府机构常常处理生命周期超过 25 年的机密信息。此外,还存在所谓的"现在存储,未来解密"攻击:攻击者可以在今天收集并保存加密通信,一旦未来拥有足够强大的量子计算机,就再进行解密。这类攻击在历史上确有先例,因此并非杞人忧天。
迁移计划的一部分,是由联邦机构协调,对可能存在风险的技术进行清点,同时由 NIST 负责推进后量子密码学的标准化工作。这最终促成了 NIST 发起一项竞赛,寻找能够同时抵抗经典和量子攻击者的算法。竞赛仍在进行中,但在 2022 年,已经看到了四个早期"优胜者"的雏形,其中三种算法的标准化工作已于 2024 年 8 月 13 日正式完成并发布。
不出所料,该迁移计划还强调了动员私营组织并推动这些标准的广泛采用。迁移往往需要很长时间(比如 Python 2 的淘汰就花了 12 年),因此提前启动会带来巨大优势。
3. 量子计算机为什么与众不同?
量子计算机基于量子比特(qubit)运算。一个理想的单个量子比特是如下基态的叠加:
- ∣ 0 ⟩ \lvert 0 \rangle ∣0⟩ 和 ∣ 1 ⟩ \lvert 1 \rangle ∣1⟩
它们对应经典计算中的比特 0 和 1,但在数学上,它们是相互正交的向量,构成一个线性向量空间的基。这意味着,一个量子比特可以表示 ∣0⟩ 和 ∣1⟩ 的任意线性组合。那么,这有什么用呢?
其中一个关键点是:
- 一个量子比特可以同时编码 0 和 1。
来看一个量子比特 φ \varphi φ 的表示形式:
- ∣ φ ⟩ = α ∣ 0 ⟩ + β ∣ 1 ⟩ \lvert \varphi \rangle = \alpha \lvert 0 \rangle + \beta \lvert 1 \rangle ∣φ⟩=α∣0⟩+β∣1⟩
按照定义, α \alpha α 和 β \beta β 是所谓的"概率振幅"(因此它们的平方之和必须等于 1)。量子比特允许处于如下状态:
- ( ∣ 0 ⟩ + ∣ 1 ⟩ ) / 2 (\lvert 0 \rangle + \lvert 1 \rangle)/\sqrt{2} (∣0⟩+∣1⟩)/2
这表示它以相等的概率同时处于 0 和 1 的状态。更重要的是,这种特性可以扩展:
- 两个量子比特可以同时编码 00、01、10 和 11;
- 随着量子比特数量增加,这种并行性会指数级增长。
这为一些"数学魔法般的算法"提供了基础:
- 这些算法能够利用这种模糊叠加态,并让其最终收敛到一个正确答案。
为了便于理解,可以把它近似看作是"并行处理所有可能状态",而这正是量子计算获得巨大加速的根本来源。
当然,事情并没有这么简单。上述定义描述的是理想量子比特,而现实世界中量子比特的各种非理想问题带来了巨大的工程挑战。量子计算机是有噪声的,误差会在长时间计算中不断累积,甚至可能完全无法产生有效结果。
到这里为止,这听起来似乎还不算太糟,接下来看量子计算机究竟能做些什么。
4. 量子算法
和经典计算机一样,一旦量子计算机被提出,人们几乎立刻就开始研究如何利用它们。果不其然,在 20 世纪 90 年代,彼得·肖尔(Peter Shor)和洛夫·格罗弗(Lov Grover)先后提出了量子算法,用于改进对经典密码算法的密码分析,使密码学成为可用量子计算机下最显著的"附带损害"。这些算法分别以他们的名字命名为 Shor 算法 和 Grover 算法,分别针对非对称密码和对称密码。
- Shor 算法(严格来说是一组算法,但由于它们在数学上几乎等价且提出时间不同,通常统称为 "Shor 算法")可以高效地解决大整数分解问题和离散对数问题。
- 与此同时,Grover 算法可以将数据库搜索的时间复杂度降低为平方根级别,从而显著提高对对称密钥和哈希函数的暴力破解效率。
- Grover 算法实现起来较为困难,而且可以通过使用 256 位密钥轻松缓解。
- 基本上,128 位密钥在 Grover 算法下需要约 2 64 2^{64} 264 次操作即可破解,而使用 256 位密钥则需要约 2 128 2^{128} 2128 次计算,这在实践中仍然是安全的。
真正严峻的挑战来自 Shor 算法,它对当前的公钥密码系统构成了致命威胁。以 RSA 为例,其正常使用本身的复杂度就与模数大小呈立方关系,而 Shor 算法在模数大小上的复杂度是多项式级别的。单纯增大密钥长度并不能有效解决问题。因此,需要新的算法,而 NIST 的竞赛已经带来了一些答案。
5. 后量子算法
在 2022 年公布(并计划后续继续补充)的算法包括:用于数字签名的 Dilithium、Falcon 和 SPHINCS+,以及用于密钥交换的 Kyber。这些算法是从大量候选方案中选出的,并分别标准化为 ML-DSA(Dilithium)、SLH-DSA(SPHINCS+) 和 ML-KEM(Kyber)。在 2022 年选中的方案中,只有 FN-DSA(Falcon) 仍在等待正式标准化。
在签名算法方面:
- NIST 明确偏向 ML-DSA,因为它更容易安全实现,且资源消耗较低。
- FN-DSA 的选择是为了满足对公钥和签名尺寸要求较小的应用场景,尽管它的实现难度很高,尤其是在资源受限设备上,同时还更容易受到侧信道攻击。
- SLH-DSA 被标准化的原因在于它是基于哈希的算法,安全性机理更为成熟;
- 而 ML-DSA 和 FN-DSA 则是基于格(lattice)的算法。
- 由于格密码相对新颖,NIST 不希望完全依赖这种新范式------尽管看起来有些矛盾,因为 ML-KEM(Kyber) 是目前唯一公布的密钥交换优胜方案,而它本身正是基于格的。
基于格的密码学起源于 20 世纪 90 年代,其安全性依赖于解决某些与格相关的数学难题的困难性,如最短向量问题(SVP)、最近向量问题(CVP),以及相关的 短基问题(SBP)、近似最短向量问题(apprSVP)、近似最近向量问题(apprCVP) 等。极大地简化来说:一个特定的格可以由不同的基来表示,其中有些基是"好"的(几乎正交且向量较短),使得上述问题容易求解;而给定一个"坏"的基(向量几乎平行且长度较大),这些问题就变得非常困难。因此,可以构造这样的公钥密码系统:公钥包含"坏"的基,允许公众将数据编码到格中的某个点;而只有掌握"好"基的私钥持有者,才能高效地解码。
这只是格密码学的基本思想。实际上,存在多种基于格的密码系统,它们在权衡、安全证明、密钥大小等方面各不相同。仅以带误差学习(LWE)为例,就有 LWE、Ring-LWE 和 Module-LWE 三种变体。若想获得直观理解,可以观看这些 Chalk Talk 视频;如果更有探索精神,也可以通过这门由先驱者讲授的 录制夏季课程An Introduction to Lattices, Lattice Reduction, and Lattice-Based Cryptography | Joseph H. Silverman, Brown University 入门。
不过,这也正是"未来补充方案"发挥作用的地方。密钥交换算法的竞赛尚未结束,尽管 Kyber 是早期赢家,NIST 仍在进行第四轮评选,以寻找替代性的密钥交换算法。在签名算法方面也出现了类似情况:由于签名尺寸和性能问题,许多人对现有选择并不满意,促使 NIST 几乎立即启动了征集更多后量子签名方案的流程。
事实上,后量子算法的一个重要特征是:
- 与经典算法相比,它们的密钥、签名和密文都要大得多。
- 这意味着在向后量子算法迁移的过程中,一个现实问题就是如何处理这些更大的数据结构------如,它们可能已经无法装入一个不分片的 IPv6 数据包中。
此外,还失去了使用 Diffie--Hellman(DH) 的能力。虽然平时不太关注这一点,但 DH 提供了非交互式密钥交换的能力,也就是说,一方可以在无需来回通信的情况下与另一方建立密钥,如在线客户端与离线客户端之间。DH 的这一特性常被用作一种认证方式,从而避免频繁交换签名。当前,人们正在积极研究能够在依赖该特性的协议中,替代 DH 的后量子方案。
格密码的新颖性也带来了另一个问题:
- 它们尚未经历与经典密码算法同等程度的长期密码分析。
为了在增强抗量子攻击能力的同时,继续利用数十年来的密码分析成果,后量子密码(PQC)算法的设计者本身就建议采用混合方案,即将经典算法与 PQC 算法结合使用。接下来,将简要看看两种常见的混合方案------即便并不真正需要理解这一部分,仍希望通过它展示混合方案背后所隐藏的复杂性:
- 混合签名方案:使用 Ed25519 的椭圆曲线签名 + 使用格算法 ML-DSA-65 的后量子签名
- 混合密钥交换方案:基于 X25519 的一次性(ephemeral)椭圆曲线 Diffie--Hellman + ML-KEM-768
5.1 为混合方案让路
混合方案1------混合签名方案:
- 将使用 Ed25519 的椭圆曲线签名与使用格算法 ML-DSA-65 的后量子签名结合在一起。
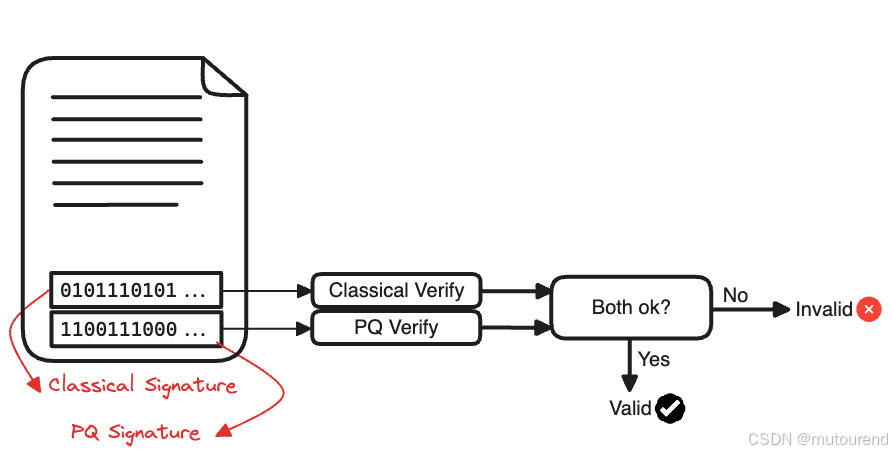
一条消息的混合签名,是使用发送方的椭圆曲线私钥和后量子私钥,对同一条消息分别生成的椭圆曲线签名与后量子签名的拼接。
在验证签名时,验证者会将签名拆分为两部分,并分别使用发送方对应的公钥进行验证;只有当两部分签名都验证通过时,整体签名才是有效的。因此,在该协议中,攻击者若想伪造签名,必须同时伪造这两种签名,这意味着该协议的安全性至少不低于两种基础原语中最安全的那一个。
混合方案2------混合密钥交换方案:
- 将椭圆曲线密码学与具备抗量子能力的、基于格的公钥密码算法结合在一起。
该协议的设计目标是:任何能够恢复派生密钥的攻击,都必须同时攻破经典密码原语和后量子密码原语。
在协议的经典部分,使用基于 X25519 的一次性(ephemeral)椭圆曲线 Diffie--Hellman。具体来说,协议中假设接收方拥有椭圆曲线公钥 P K r e c PK_{r}^{ec} PKrec,并生成一个一次性的椭圆曲线密钥对 ( S K e p h e c , P K e p h e c ) (SK_{eph}^{ec},PK_{eph}^{ec}) (SKephec,PKephec)
然后,计算椭圆曲线共享秘密:
s s e c = X 25519 ( S K e p h e c , P K r e c ) ss_{ec} = X25519(SK_{eph}^{ec}, PK_{r}^{ec}) ssec=X25519(SKephec,PKrec)
对于后量子部分,使用 ML-KEM-768。给定接收方的后量子公钥 P K r p q PK_{r}^{pq} PKrpq ,计算密文 C p q C_{pq} Cpq 和后量子共享秘密 s s p q ss_{pq} sspq ,其中:
s s p q = E N C ( P K r p q ) ss_{pq} = ENC(PK_{r}^{pq}) sspq=ENC(PKrpq)
其中, E N C ENC ENC 是 ML-KEM-768 密钥封装函数。
通过这两个共享密钥,使用 KDF 计算共享的 256 位密钥 K E K_E KE ,并构建一个双重伪随机函数(dual PRF),该函数将共享密钥作为输入。dual PRF 是一个接受两个密钥和一个输入的函数,使得如果攻击者控制其中一个密钥,输出仍然与随机值无法区分。有多种方法可以通过 KDF 构造dual PRF,下面的图示就是其中之一:
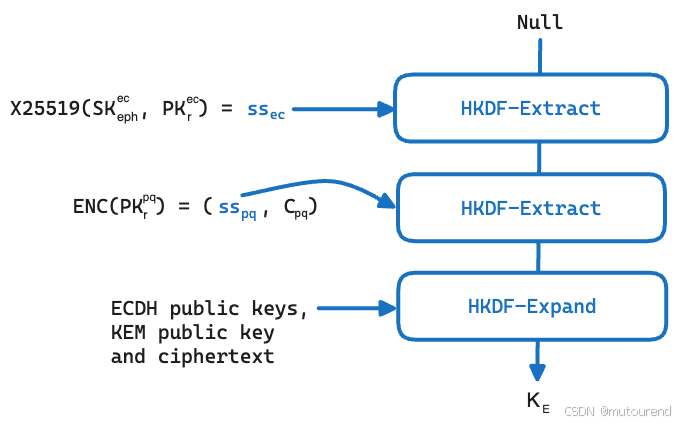
于是,公式为:
K E = K D F s s e c , s s p q ( P K r p q ∥ C p q ∥ P K r e c ∥ P K e p h e c ) K_E = KDF_{ss_{ec}, ss_{pq}}(PK_{r}^{pq} \parallel C_{pq} \parallel PK_{r}^{ec} \parallel PK_{eph}^{ec}) KE=KDFssec,sspq(PKrpq∥Cpq∥PKrec∥PKephec)
该协议返回密钥 K E K_E KE 、临时椭圆曲线公钥 P K e p h e c PK_{eph}^{ec} PKephec 和后量子封装密文 C p q C_{pq} Cpq 。
然后, K E K_E KE 被用于派生加密明文的密钥和随机数。接着,需要将 P K e p h e c PK_{eph}^{ec} PKephec 和 C p q C_{pq} Cpq 发送给接收方,以便其能够恢复 K E K_E KE 用于解密。
接收方通过三个步骤恢复密钥 K E K_E KE 。
- 首先,接收方使用其私钥 S K r e c SK_{r}^{ec} SKrec 和接收到的临时公钥 P K e p h e c PK_{eph}^{ec} PKephec ,执行椭圆曲线 Diffie-Hellman,得到第一个共享秘密:
s s e c = X 25519 ( S K r e c , P K e p h e c ) ss_{ec} = X25519(SK_{r}^{ec}, PK_{eph}^{ec}) ssec=X25519(SKrec,PKephec) - 然后,使用密文 C p q C_{pq} Cpq 和其私钥 S K r p q SK_{r}^{pq} SKrpq ,接收方能够恢复第二个共享秘密:
s s p q = D E C ( C p q , S K r p q ) ss_{pq }= DEC(C_{pq}, SK_{r}^{pq}) sspq=DEC(Cpq,SKrpq)
这一步使用 ML-KEM-768 密钥解封装函数(Key Decapsulation function)完成。 - 通过以上两个共享秘密,可以得到最终的密钥 K E K_E KE :
K E = K D F s s e c , s s p q ( P K r p q ∥ C p q ∥ P K r e c ∥ P K e p h e c ) K_E = KDF_{ss_{ec}, ss_{pq}}(PK_{r}^{pq} \parallel C_{pq} \parallel PK_{r}^{ec} \parallel PK_{eph}^{ec}) KE=KDFssec,sspq(PKrpq∥Cpq∥PKrec∥PKephec)
注意,还将后量子公钥和密文关联起来,原因是密钥封装易受到单一密钥泄露伪装攻击,将派生的密钥与接收方的公钥绑定可以解决这个问题,Kyber有防护机制,但这意味着不需要直接信任它,而是可以重用旧的密钥封装证明并继续进行。类似地,将密文绑定使得可以更容易地声明该协议能有效防范选择密文攻击。为了安全起见,还将其他所有因素也绑定起来。
6. 该如何应对?
关于迁移到后量子加密(PQC),许多重要的变更可能不直接依赖于应用系统开发者;它们由底层库和基础设施控制。然而,应用系统开发者需要识别出依赖公钥加密的地方,并确定是否有任何长期变化是开发者需要准备的。如,在混合协议中,既需要经典的密钥对,也需要后量子的密钥对,而后量子密钥比经典密钥大四个数量级。
那么,该应用系统是否依赖于运行这些算法的低端设备?是否有足够的带宽来处理较大的公钥和签名/密文大小?是否有足够的处理能力来应对额外的工作负载?这些是目前需要考虑的问题。加密提取和密钥派生:如,HKDF方案和后量子签名存在一些微妙的权衡。但如果急需快速签名和验证,将不得不为此付出较大的公钥大小和/或签名,反之亦然。SQIsign 是一个在数字签名中颇受青睐的算法,其公钥为128字节,签名为335字节,但签名过程需要高达1280亿次计算周期。即便是在新一轮竞赛中,数字签名方案似乎也无法成为万能解。幸运的是,大多数数字签名的应用并不急于实现后量子安全,至少不像密钥交换那样急需,这使得它们能接受更多的权衡。
以下两张表格,可帮助了解这些变更的影响。这些表格是从NIST的提交中编译的,同时也加入了Curve25519作为对比。需要注意的是,签名是使用Haswell处理器进行的,而密钥交换是在Coffee Lake上进行的。还找到了Curve25519在这些微架构上的基准数据。但Latacora团队计划通过在相同的CPU上运行自己的基准测试来更新这些数据,这样也可以帮助测量内存占用。
| 算法 | NIST安全级别 | 私钥大小 | 公钥大小 | 签名大小 | 周期(签名/验证) |
|---|---|---|---|---|---|
| ML-DSA-44 | 2 | 2528 | 1312 | 2420 | 333k/118k |
| ML-DSA-65 | 3 | 4000 | 1952 | 3293 | 529k/179k |
| ML-DSA-87 | 5 | 4864 | 2592 | 4595 | 642k/279k |
| Falcon-512 | 1 | 1281 | 897 | 666 | 1M/80k |
| Falcon-1024 | 5 | 2305 | 1793 | 1280 | 2M/160k |
| Ed25519 | 1 | 32 | 32 | 64 | 42k/130k |
| 算法 | NIST安全级别 | 私钥大小 | 公钥大小 | 密文大小 | 周期(加密/解密) |
|---|---|---|---|---|---|
| ML-KEM-512 | 1 | 1632 | 800 | 768 | 45k/59k |
| ML-KEM-768 | 3 | 2400 | 1184 | 1088 | 68k/82k |
| ML-KEM-1024 | 5 | 3168 | 1568 | 1568 | 97k/115k |
| X25519 | 1 | 32 | 32 | - | 125k/125k |
其中NIST安全级别描述:
- 1 - 至少和 AES128 一样难破解;
- 2 - 至少和 SHA256 一样难破解;
- 3 - 至少和 AES192 一样难破解;
- 4 - 至少和 SHA384 一样难破解;
- 5 - 至少和 AES256 一样难破解。
7. 现实世界中的后量子示例
一些应用程序已经在开辟这片新天地,现实世界中的后量子示例有:
- 1)OpenSSH
自版本9起,它们默认使用了后量子混合协议。 - 2)Chrome
可以访问chrome://flags/并启用TLS 1.3混合支持Kyber,这实现了TLS混合草案提案。 - 3)Firefox Nightly
可以在about:config中启用security.tls.enable_kyber。 - 4)BoringSSL
已经实现了 X25519+Kyber768,并且一直在尝试加入 Dilithium 支持(遇到了一些困难)。因此,可以使用编译了 BoringSSL 的 nginx 版本来支持这些功能。 - 5)Open Quantum Safe
一组常用库的分支,旨在支持 PQC 算法。 - 6)Zig
如果对新兴编程语言感兴趣,Zig是一个有趣的选择。自版本 0.11 起,Zig的加密库已经支持后量子算法。 - 7)Signal
libsignal 和 Signal 应用程序已经对其密钥协商协议进行了更新,使其支持后量子加密。X3DH 现在变成了 PQXDH。 - 8)iMessage
iMessage 使用一种名为 PQ3 的后量子密钥协商协议。与 PQXDH 非常相似。
8. PQC 正确答案
8.1 加密数据
加密数据相关正确答案为:
- Latacora, 2018: KMS 或 XSalsa20+Poly1305。
- Latacora, 2024: KMS 或 XSalsa20+Poly1305。
Grover 算法对 256 位密钥的影响并不严重。它对于 192 位和 256 位密钥的实现较为困难,因为它是一个长时间的串行计算,量子计算机似乎对此非常不喜欢,尤其是错误传播问题。即使忽略所有这些实际问题,仍然会将 256 位的边际安全性降到 128 位,但这依然是可以接受的。
实际上,如果担心加密、密钥长度、对称"签名"、哈希、随机 ID、密码处理、在线备份等问题,Latacora团队的观点并没有像之前的文章那样发生太大变化。
在此不会深入讨论细节,因为自上次以来,动机并没有变化。但简而言之,如果有机会使用 KMS,应该使用它。它将节省时间,并减少与密钥管理相关的麻烦。这些服务通常已经获得 HIPAA、FedRAMP 等认证,如果是小公司,这有助于更快地勾选各种要求。
如果无法使用 KMS,还有很多不错的选择。选择 XSalsa20+Poly1305 有很多原因。它是 libsodium 的默认方案,因此很容易找到对应的语言绑定。它拥有扩展的 nonce,这意味着可以使用随机的 nonce 而不必担心。
还有其他好的选择吗?当然,但个人认为更愿意将时间花在别的地方,而不是担心在一个密钥下触发多少次 AES-GCM 加密。
避免:
- 非认证加密。很少有应用程序有正当理由跳过认证加密,通常是因为其他机制提供了认证。
8.2 对称密钥长度
对称密钥长度相关正确答案为:
- Latacora, 2018: 256 位密钥。
- Latacora, 2024: 256 位密钥。
这对于后量子加密很重要。对于经典加密而言,选择较小的密钥并不会带来显著的性能提升。使用 256 位密钥意味着不必担心多目标攻击或其他可能遇到的奇怪场景。
避免:
- 过大的密钥,密码"级联"。
8.3 哈希算法
哈希算法相关正确答案为:
- Latacora, 2018: SHA-2。
- Latacora, 2024: SHA-2。
不过,在此不会对使用 SHA-3 或 Blake2/3 的人进行评判,SHA 因为得到 NIST 的批准,并且几乎在任何地方都能找到,确实有一些优势。Latacora团队非常喜欢 Blake,但是开发者可能不想将其依赖于 GitHub 上的随机用户来将其移植到每个新出现的流行语言,而 SHA 通常是标准库的一部分。
此外,截断版本具有额外的防止长度扩展攻击的保护,因为攻击者看到的哈希不是函数的完整状态,因此无法重新启动。因此,可以使用 SHA-512/256,从而避免开发者在序列化不良的字符串上进行哈希操作。
避免:
- SHA-1、MD5 和 MD6。
8.4 对称"签名"
对称"签名"相关正确答案为:
- Latacora, 2018: HMAC。
- Latacora, 2024: 仍然是 HMAC。
HMAC 无处不在。这里保持简单很重要,因为 HMAC 有几个关键应用:保护 API、cookie、令牌等。同样重要的是使用一个时间常量函数来比较标签,提供 HMAC 的良好库通常也提供安全的比较函数。
避免:
- HMAC-MD5、HMAC-SHA1 等。底层的哈希函数必须是安全的。
8.5 随机 ID
随机 ID相关正确答案为:
- Latacora, 2018: 使用 256 位的随机数。
- Latacora, 2024: 使用 256 位的随机数。不过要小心来源,使用
/dev/urandom。
避免:
- 使用用户空间的随机数生成器,如 OpenSSL RNG、havaged、prngd、egd 或
/dev/random。
8.6 密码处理
密码处理相关正确答案为:
- Latacora, 2018: 按优先级顺序使用 scrypt、argon2、bcrypt,如果没有其他选择,使用 PBKDF2。
- Latacora, 2024: 小变化。按优先级顺序使用 argon2id、scrypt、bcrypt,仅在 FIPS 合规性强制要求时才使用 PBKDF2。
这些变化背后有几个动因。
- 首先,scrypt 的密码分析已经取得进展,发现了一些侧信道攻击。
- argon2 的密码分析也有所进展,其中 i 和 d 变体的安全性边际有所减小,但 id 变体仍然是安全的选择。现在,它不仅在 GPU 攻击和侧信道抗性之间取得了平衡,而且还保持了更好的安全边际。
避免:
- 普通的密码学哈希,如任何 SHA、任何 Blake、任何 MD。
8.7 Diffie-Hellman 密钥交换
Diffie-Hellman 密钥交换相关正确答案为:
- Latacora, 2018: 可能没什么变化,或者使用 Curve25519。
- Latacora, 2024: X25519+ML-KEM-768,或者如果担心合规问题,可以使用 P256+ML-KEM-768。
曾经有一个后量子 Diffie-Hellman 方案,但它在 2022 年被攻破了------使用一台 i5 笔记本电脑一天就能破解它。虽然有 CSIDH,可能在某个时刻会有所作为,但它已经被部分弃用,可能是因为难以找到合适的参数来实现所需的安全边际,所以它并不适用。最终需要将" Diffie-Hellman密钥交换"重命名为"密钥交换"。
现在,不要不必要地加速进程。虽然应该在可以使用 X25519+ML-KEM-768 时尽早过渡,但不应在 GitHub 上寻找仓库自己尝试拼凑。如果可能的话,等待一个主流库来公开支持这一方案。
当然,如果可以通过 Noise 框架运行预共享密钥,那么实际上就依赖于对称加密,并且只要使用 256 位密钥,将具备后量子安全性。如,WireGuard 就有一个预共享对称密钥功能。现在,Signal、iMessage 和一些浏览器已经具备后量子安全性,因此有办法"预共享"密钥。如果只是想设置一个 WireGuard 服务,这是一个绕过这个问题的合理方法。
如果迫切需要一个非交互式的后量子方案,目前人们正在尝试使用像 Swoosh 这样的协议来实现非交互式密钥交换。这些协议可以填补后量子 Diffie-Hellman 缺失所带来的空白。但这还只是刚刚起步,可能会遇到问题。
避免:
- 至少再等一段时间,不要使用纯 ML-KEM 实现。使用 Kyber 类似于使用 Rijndael 代替 AES,可能会在审计时遇到麻烦。
8.8 非对称签名
非对称签名相关正确答案为:
- Latacora, 2018: 使用 NaCl 或 Ed25519。
- Latacora, 2024: 对于大多数应用,可能可以继续使用 2018 年的建议,大多数签名密钥生命周期较短,这意味着它不容易受到"harvest now, decrypt later 现在收割,稍后解密"的威胁。
如果出于某种原因必须处理长期有效的密钥和签名,建议使用 Ed25519+ML-DSA-65,或者如果依赖于获得政府的批准,则使用 P256+ML-DSA-65。
另外,后量子 Diffie-Hellman 的一些漏洞可以通过签名来弥补。因此,如果希望实现通过静态 DH 密钥提供的可否认身份验证,将不得不设置一些巧妙的方案,比如环签名或指定验证者签名。但如果能保持简单,那就保持简单。密码学不是用来搞花样的,至少不在没有专家帮助的情况下。
避免:
- 再次避免使用纯 ML-DSA 实现。使用 Dilithium 实现代替 ML-DSA。
8.9 非对称加密
非对称加密相关正确答案为:
- Latacora, 2018: 使用 NaCl/libsodium(box / crypto_box)。
- Latacora, 2024: 好吧,这个有点复杂,因为它受量子计算的影响。如果真的依赖于加密数据,有一些方案可以实现,即如第一部分中所述进行混合密钥交换,并在 AEAD 中使用该密钥,基本上就是"hybrid_pq_crypto_box"或"PQ-HPKE"。但是,如果可能的话,建议等到成熟的密码学库实现这些方案。
libsodium 的维护者表示,一旦一切就绪,他们会实现这一功能。考虑到 ML-KEM 标准刚刚发布,这应该很快就会实现。同样的情况也适用于 Go 的加密库,预计它会实现 PQ HPKE。
8.10 网站安全
网站安全相关正确答案为:
- Latacora, 2018: 使用 AWS ALB/ELB 或 OpenSSL 配合 LetsEncrypt。
- Latacora, 2024: 同样的建议。
老实说,关于后量子加密,这可能不完全取决于应用开发者。客户端和 TLS 提供商需要实现带有混合密钥交换的密码套件。目前,建议保持之前的建议。
不过,有一些地方可以开始尝试,并尽早了解具体应用系统如何处理这些变更。
也有一些 BoringSSL 和 OpenSSL 的分支,供测试使用,维护者还修改了客户端,使其支持后量子混合方案。像 curl、nginx、haproxy、Chromium 等客户端也进行了修改。如果使用 Chrome 或 Firefox Nightly,可以启用混合化的 Kyber 支持,正如上面所展示的,记住这些是实验性功能,支持有限,但大多数 Google 服务已支持它。
如果使用 AWS,可以使用他们的 s2n-tls 实现,该实现支持混合密钥交换方案。AWS 证书管理器也在尝试后量子方案。
避免:
- 使用第三方、冷门的 TLS 库。
8.11 客户端-服务器应用安全
客户端-服务器应用安全相关正确答案为:
- Latacora, 2018: 使用 AWS ALB/ELB 或 OpenSSL 配合 LetsEncrypt。
- Latacora, 2024: 同样的建议。
继续使用 AWS ALB/ELB 或 OpenSSL 配合 LetsEncrypt。每个人都在准备发布混合的后量子方案。
在 2018 年,还讨论了 TLS 1.2+、Curve25519 和 ChaChaPoly,这些依然有效。而现在在 2024 年,TLS 1.3 也很不错,协议本身保证了前向保密性。
避免:
- 设计自己的加密传输,这是一个真正困难的工程问题;在默认配置下使用 TLS 1.3 以下版本,比如使用 "curl";使用 "curl" 和 IPSEC。
8.12 在线备份
在线备份相关正确答案为:
- Latacora, 2018: Tarsnap。
- Latacora, 2024: Tarsnap。
参考资料
1\] Latacora团队2024年8月博客[Cryptographic Right Answers: Post Quantum Edition](https://www.latacora.com/blog/post-quantum-cryptographic-right-answers/)