part4 反向传播算法(BP算法)

wjykp2025-12-27 9:09

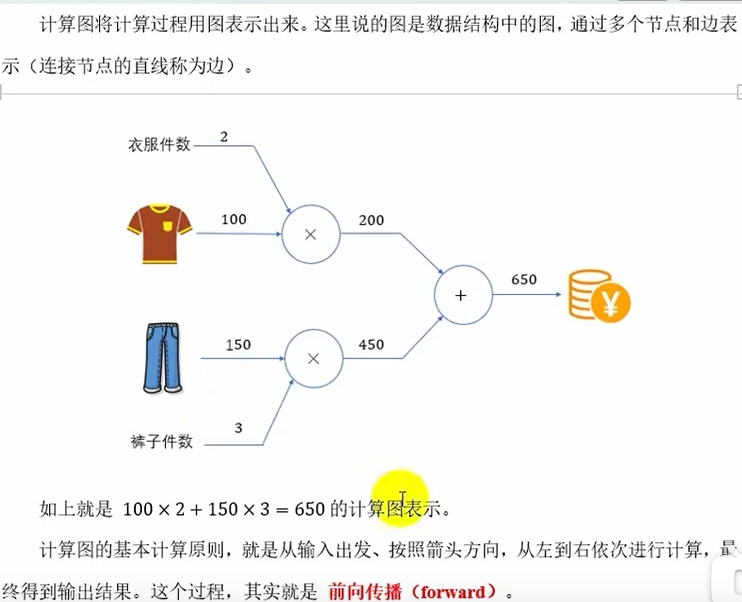
计算图

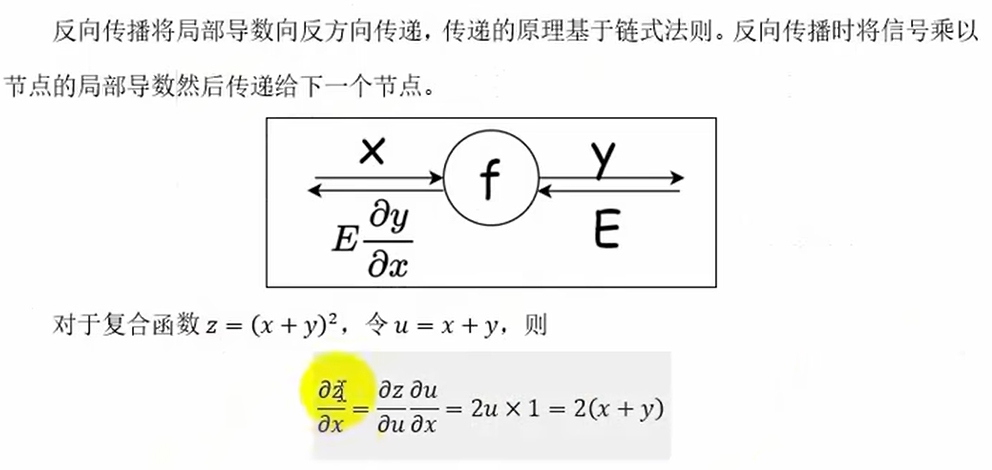
BP算法是指计算神经网络参数梯度的方法，该方法根据微积分中的链式法则，按相反的顺序从输出层到输入层遍历网络。该算法存储了计算某些参数梯度时所需的任何中间变量

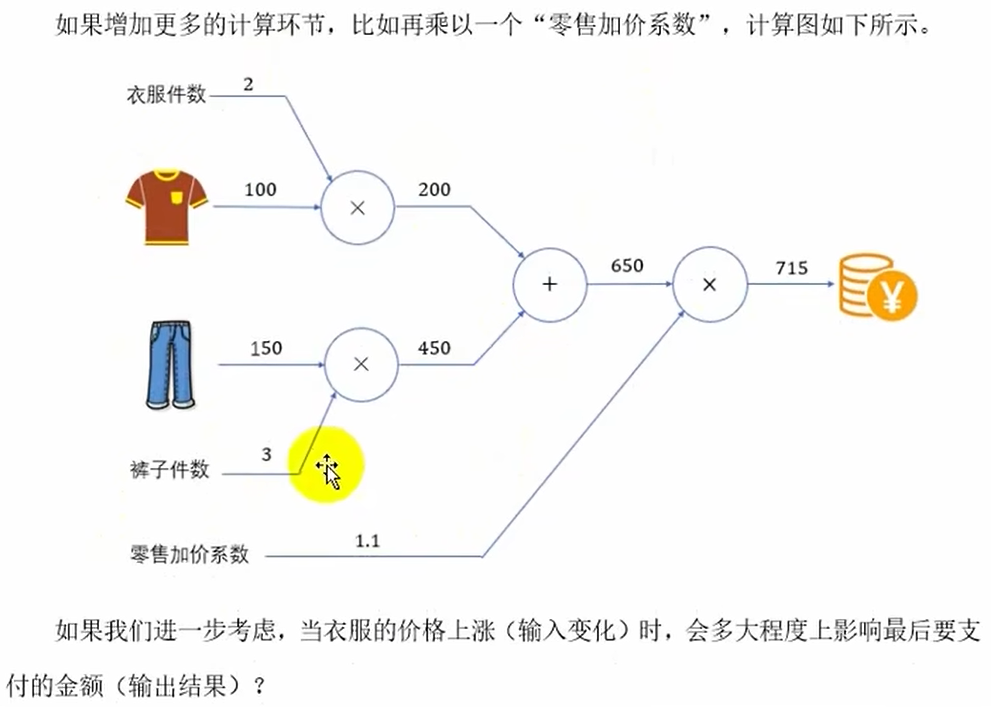
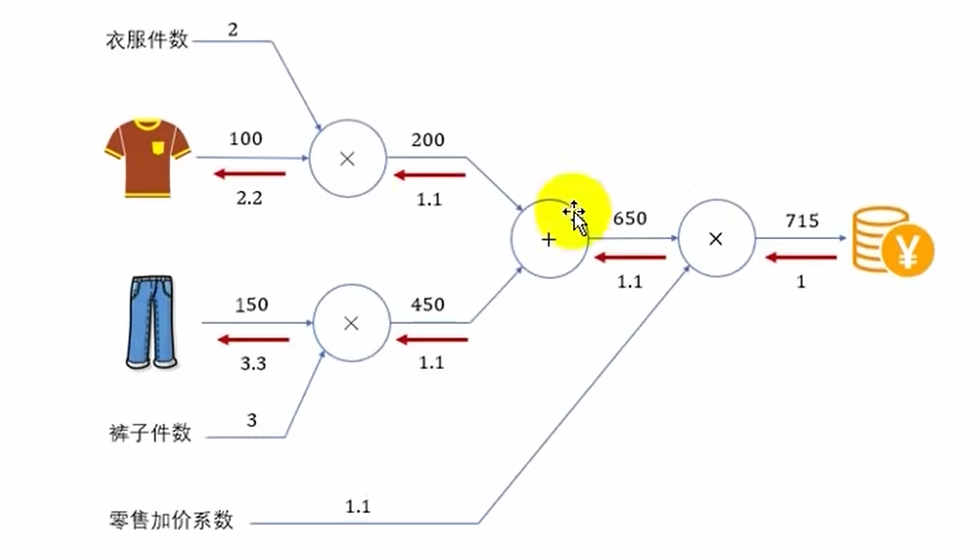
链式法则

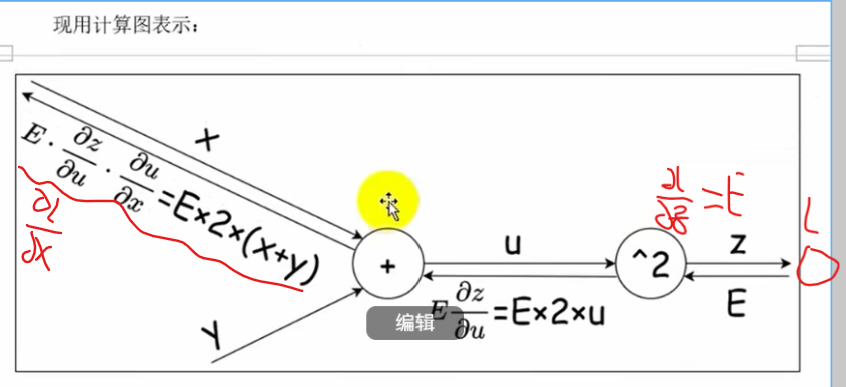
反向传播

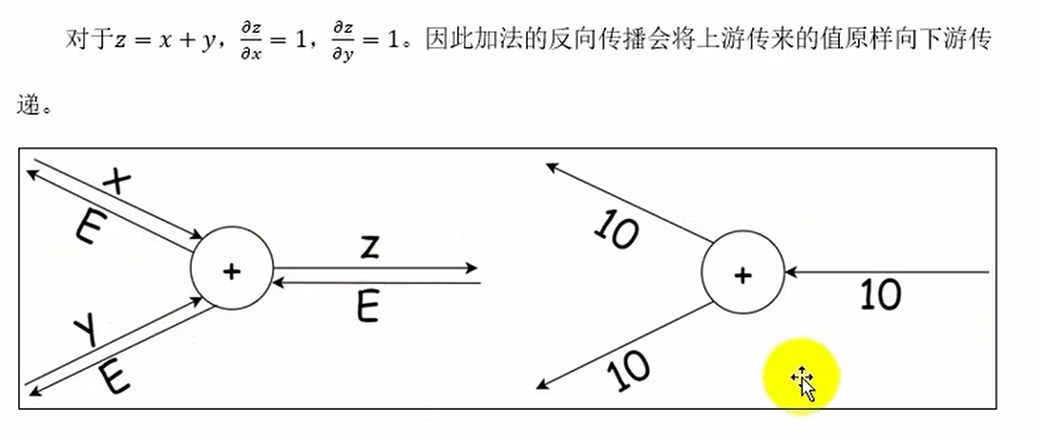
加法节点的反向传播(不变)

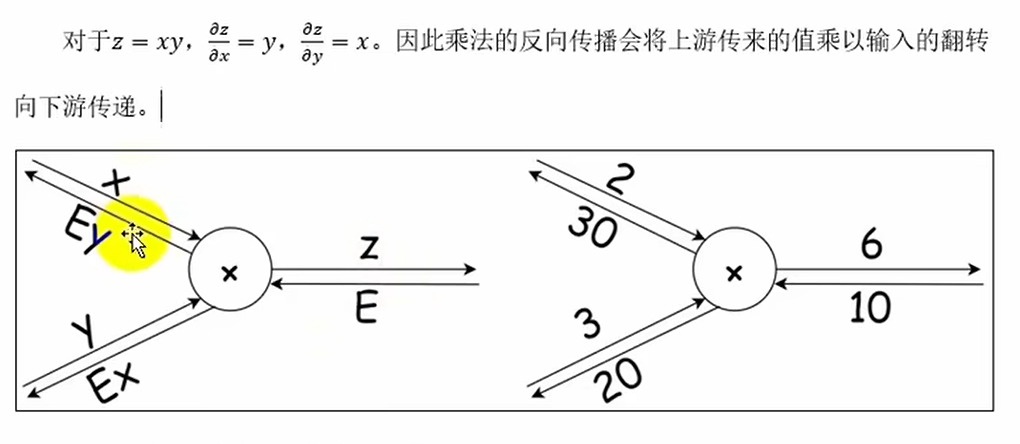
乘法节点的反向传播

激活层的反向传播与实现

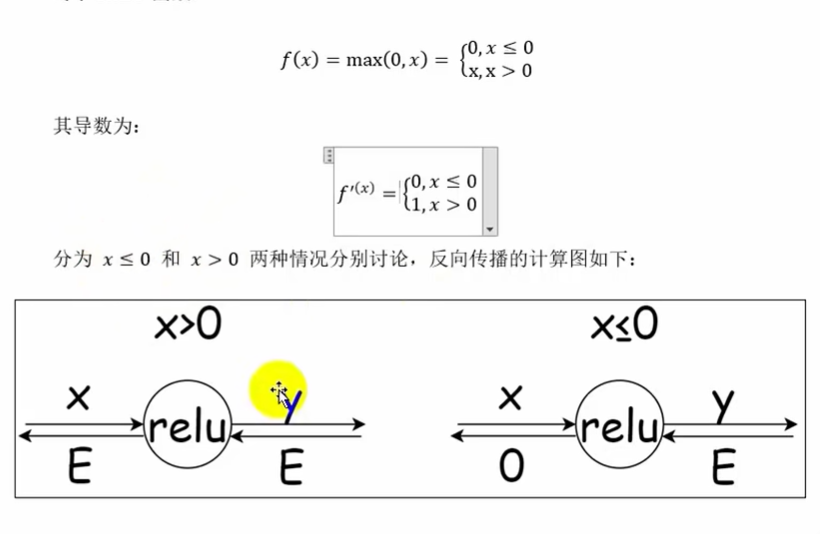
ReLU的反向传播

复制代码 
from common.functions import *
# ReLU
class ReLu:
    # 初始化
    def __init__(self):
        # 内部属性，记录哪些x<=0
        self.mask=None # mask中存true or false
    # 前向传播
    def forward(self,x):
        # 如果x是[-1, 0, 2]，那么self.mask就是[True, True, False]
        self.mask=(x<=0)
        y=x.copy()
        # 将y中所有对应掩码为True的位置（即x中小于等于0的位置）的值设置为0
        y[self.mask]=0
        return y
    # 反向传播
    # dy是上游传递过来的导数值，就是那个E
    def backward(self,dy):
        dx=dy.copy()
        dx[self.mask]=0
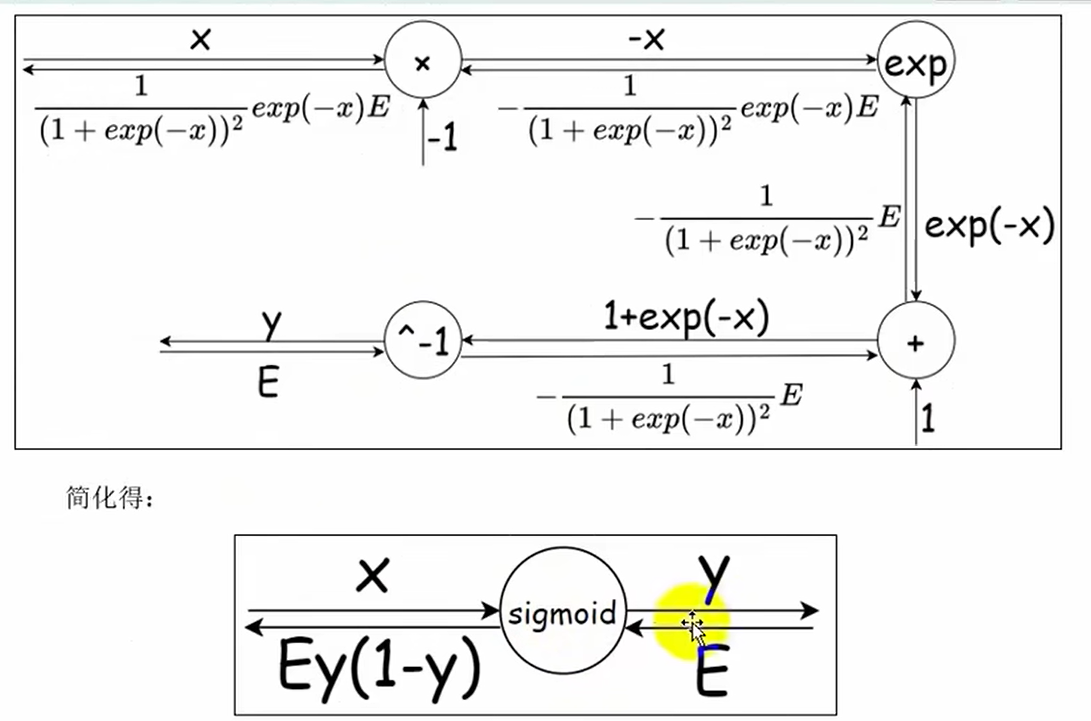
        return dx

Sigmoid的反向传播

复制代码 
# Sigmoid
class Sigmoid:
    # 初始化
    def __init__(self):
        # 定义内部属性，记录输出值y,用于反向传播时计算梯度
        self.y=None
    # 前向传播
    def forward(self,x):
        y=sigmoid(x)
        self.y=y
        return y
    # 反向传播
    # dy是上游传递过来的导数值，就是那个E
    def backward(self,dy):
        dx=dy*self.y*(1.0-self.y)
        return dx

Affine层的反向传播与实现

L对X求导：L损失函数是标量，Y形状是N*n，L对Y求导形状也是N*n,Y对X求导得W'(n*m),所以是右乘W'

L对W求导：L损失函数是标量，L对Y求导形状是N*n,Y对W求导X'的形状是(m*N),所以是左乘X'

复制代码 
# Affine 仿射层y=xw+b
class Affine:
    # 初始化
    def __init__(self,W,b):
        self.W=W
        self.b=b
        # 对输入数据X做保存，方便反向传播计算梯度
        self.X=None
        self.original_x_shape=None
        # 将权重和偏置参数的梯度(偏导数)保存成属性，方便梯度下降法计算
        self.dW=None
        self.db=None # 因为dx是反向传播的返回，所以初始化就不单独保存了
    # 前向传播
    def forward(self,X):
        self.original_x_shape=X.shape
        self.X=X.reshape(X.shape[0],-1)
        y=np.dot(self.X,self.W)+self.b
        return y
    # 反向传播 dy-->E dX-->EW'
    def backward(self,dy):
        dX=np.dot(dy,self.W.T)
        dX=dX.reshape(*self.original_x_shape)
        self.dW=np.dot(self.X.T,dy)
        self.db=np.sum(dy,axis=0)
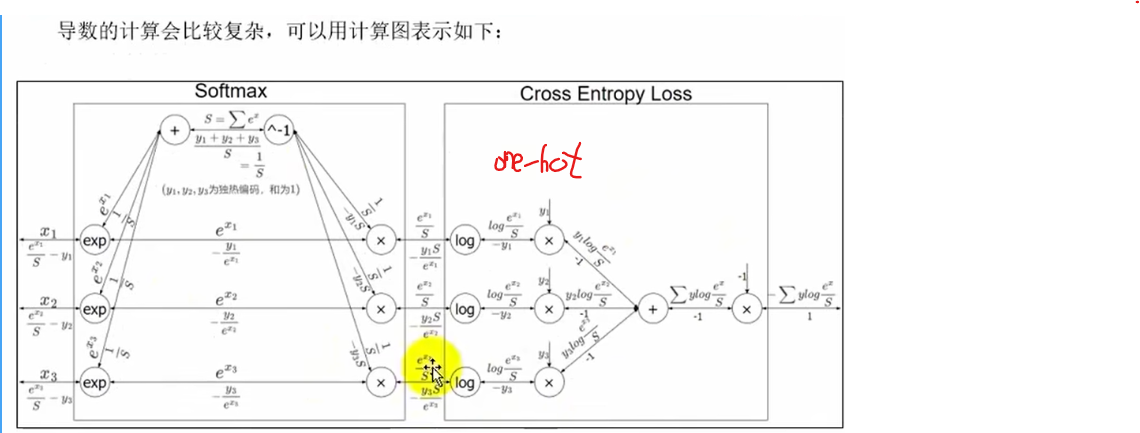
        return dX

输出层的反向传播与实现

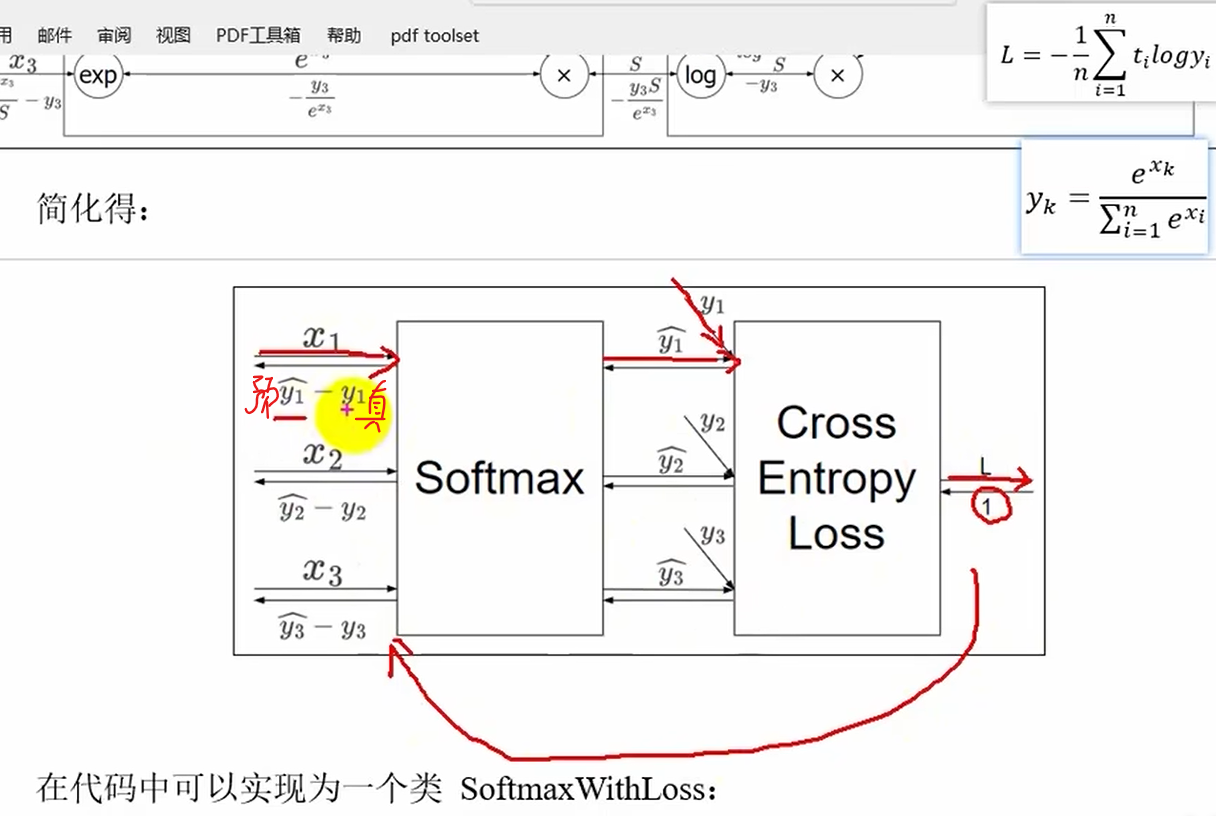
y^-->y 预测值

y-->t 真实值

复制代码 
# 输出层
class SoftmaxWithLoss:
    def __init__(self):
        self.loss=None
        self.y=None # 预测值
        self.t=None # 真实值
    # 前向传播
    def forward(self,X,t):
        self.t=t
        self.y=softmax(X)
        self.loss=cross_entropy(self.y,self.t)
        return self.loss
    # 反向传播 dy=dl/dy
    def backward(self,dy=1):
        n=self.t.shape[0] # 数据个数
        # 如果是独热编码标签，就直接带入公式计算
        if self.t.size==self.y.size:
            dx=self.y-self.t # y是n个数据，每个数据m个概率值 t是0101...
        # 如果是顺序编码的标签，就需要找到分类号对应的值，然后相减
        else:
            dx=self.y.copy()
            dx[np.arange(n),self.t]-=1 # 花式(列表)索引
        return dx/n # 前面的loss没有/n

反向传播综合案例

TwoLayerNet

复制代码 
import numpy as np
from common.functions import softmax,sigmoid,cross_entropy
from common.gradient import numerical_gradient
from common.layers import * # 反向传播的层
from collections import OrderedDict # 有序字典，用来保存各个层的结构并给出顺序
class TwoLayerNet:
    # 初始化 全0偏置b
    def __init__(self,input_size,hidden_size,output_size,weight_init_std=0.01):
        self.params={}
        self.params['W1']=weight_init_std*np.random.randn(input_size,hidden_size)
        self.params['b1']=np.zeros(hidden_size)
        self.params['W2']=weight_init_std*np.random.randn(hidden_size,output_size)
        self.params['b2'] = np.zeros(output_size)
        # 定义（反向传播用的）层结构
        self.layers=OrderedDict()
        self.layers['Affine1']=Affine(self.params['W1'],self.params['b1'])
        self.layers['ReLU1']=ReLu()
        self.layers['Affine2']=Affine(self.params['W2'],self.params['b2'])
        # 单独定义最后一层：SoftmaxWithLoss
        self.lastLayer=SoftmaxWithLoss()
    # 前向传播(预测)
    def forward(self,X):
        # W1,W2=self.params["W1"],self.params['W2']
        # b1,b2=self.params['b1'],self.params['b2']
        # a1=X@W1+b1
        # z=sigmoid(a1)
        # a2=z@W2+b2
        # y=softmax(a2)
        # return y
        # 对于神经网络中的每一层依次调用forward方法
        for layer in self.layers.values():
            X=layer.forward(X)
        return X
    # 计算损失
    def loss(self,x,t):
        y_pred=self.forward(x) # 最后层的输入,不是最后一层输出的概率
        loss_value=self.lastLayer.forward(y_pred,t)
        return loss_value
    # 计算准确度,t是分类号
    def accuracy(self,x,t):
        # 预测分类数值：最后层的输入,不是最后一层输出的概率但是与softmax后的结果也可以得出最大概率得到预测的分类号
        y_proba=self.forward(x)
        # 根据最大概率得到预测的分类号
        y_pred=np.argmax(y_proba,axis=1)
        # 与正确解标签对比，得到准确率
        accuracy=np.sum(y_pred==t)/x.shape[0]
        return accuracy
    # # 计算梯度f(w...)--Loss(w...)，使用数值微分方法
    # def numerical_gradient(self,x,t):
    #     # 定义目标函数
    #     loss_f=lambda w:self.loss(x,t)
    #     # 对每个参数使用数值微分方法计算梯度
    #     grads={}
    #     grads['W1']=numerical_gradient(loss_f,self.params['W1'])
    #     grads['W2'] = numerical_gradient(loss_f, self.params['W2'])
    #     grads['b1'] = numerical_gradient(loss_f, self.params['b1'])
    #     grads['b2'] = numerical_gradient(loss_f, self.params['b2'])
    #     return grads

    # 计算梯度，使用反向传播法计算梯度
    def gradient(self,x,t):
        # 前向传播，直接得到了每一层的所有参数
        self.loss(x,t)
        # 反向传播softmax and cee层
        # Loss(w..)=Σtlogyi dy=dL/dy
        dy=1
        dy=self.lastLayer.backward(dy)
        # 将神经网络中的所有层反向处理
        # 将字典的values存入list中
        layers=list(self.layers.values())
        layers.reverse()
        for layer in layers:
            dy=layer.backward(dy)
        # 提取各层参数梯度
        grads={}
        grads['W1'],grads['b1']=self.layers['Affine1'].dW,self.layers['Affine1'].db
        grads['W2'], grads['b2'] = self.layers['Affine2'].dW, self.layers['Affine2'].db

layers

复制代码 
import numpy as np

from common.functions import *
# ReLU
class ReLu:
    # 初始化
    def __init__(self):
        # 内部属性，记录哪些x<=0
        self.mask=None # mask中存true or false
    # 前向传播
    def forward(self,x):
        # 如果x是[-1, 0, 2]，那么self.mask就是[True, True, False]
        self.mask=(x<=0)
        y=x.copy()
        # 将y中所有对应掩码为True的位置（即x中小于等于0的位置）的值设置为0
        y[self.mask]=0
        return y
    # 反向传播
    # dy是上游传递过来的导数值，就是那个E
    def backward(self,dy):
        dx=dy.copy()
        dx[self.mask]=0
        return dx
# Sigmoid
class Sigmoid:
    # 初始化
    def __init__(self):
        # 定义内部属性，记录输出值y,用于反向传播时计算梯度
        self.y=None
    # 前向传播
    def forward(self,x):
        y=sigmoid(x)
        self.y=y
        return y
    # 反向传播
    # dy是上游传递过来的导数值，就是那个E
    def backward(self,dy):
        dx=dy*self.y*(1.0-self.y)
        return dx
# Affine 仿射层y=xw+b
class Affine:
    # 初始化
    def __init__(self,W,b):
        self.W=W
        self.b=b
        # 对输入数据X做保存，方便反向传播计算梯度
        self.X=None
        self.original_x_shape=None
        # 将权重和偏置参数的梯度(偏导数)保存成属性，方便梯度下降法计算
        self.dW=None
        self.db=None # 因为dx是反向传播的返回，所以初始化就不单独保存了
    # 前向传播
    def forward(self,X):
        self.original_x_shape=X.shape
        self.X=X.reshape(X.shape[0],-1)
        y=np.dot(self.X,self.W)+self.b
        return y
    # 反向传播 dy-->E dX-->EW'
    def backward(self,dy):
        dX=np.dot(dy,self.W.T)
        dX=dX.reshape(*self.original_x_shape)
        self.dW=np.dot(self.X.T,dy)
        self.db=np.sum(dy,axis=0)
        return dX
# 输出层
class SoftmaxWithLoss:
    def __init__(self):
        self.loss=None
        self.y=None # 预测值
        self.t=None # 真实值
    # 前向传播
    def forward(self,X,t):
        self.t=t
        self.y=softmax(X)
        self.loss=cross_entropy(self.y,self.t)
        return self.loss
    # 反向传播 dy=dl/dy
    def backward(self,dy=1):
        n=self.t.shape[0] # 数据个数
        # 如果是独热编码标签，就直接带入公式计算
        if self.t.size==self.y.size:
            dx=self.y-self.t # y是n个数据，每个数据m个概率值 t是0101...
        # 如果是顺序编码的标签，就需要找到分类号对应的值，然后相减
        else:
            dx=self.y.copy()
            dx[np.arange(n),self.t]-=1 # 花式(列表)索引
        return dx/n # 前面的loss没有/n

load_data

复制代码 
import pandas as pd
import numpy as np
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split
# 读取数据
def get_data():
    # 1.从文件内加载数据集dataframe
    data=pd.read_csv("../data/train.csv")
    # 2.划分数据集
    x=data.drop("label",axis=1) # axis=1是跨列
    y=data["label"]
    x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.3,random_state=42)
    # 3.特征工程：归一化
    scaler=MinMaxScaler()
    x_train=scaler.fit_transform(x_train)
    x_test=scaler.transform(x_test)
    # 4.将数据都转成ndarraqy
    y_train=y_train.values
    y_test=y_test.values
    return x_train,x_test,y_train,y_test

1_digit_recognizer_nn_train_bp

复制代码 
import numpy as np
import matplotlib.pyplot as plt
from two_layer_net import TwoLayerNet # 两层神经网络类
from common.load_data import get_data
# 1.加载数据
x_train,x_test,t_train,t_test=get_data()
# 2.创建模型
network=TwoLayerNet(input_size=784,hidden_size=50,output_size=10)# 784个像素点，每个像素点可能有10种
# 3.设置超参数
learning_rate=0.1
batch_size=100
num_epochs=10
train_size=x_train.shape[0]
iter_per_epoch=np.ceil(train_size/batch_size) # np.cell 向上取整
iters_num=int(num_epochs*iter_per_epoch) # 总迭代次数,转成int，才能给到range里面
train_loss_list=[]
train_acc_list=[]
test_acc_list=[]
# 4.循环迭代，梯度下降法训练模型
for i in range(iters_num):
    # 4.1随机选取批量数据(从train_size中随机选择batch_size)
    # batch_mask是一个数组
    batch_mask=np.random.choice(train_size,batch_size)
    x_batch=x_train[batch_mask]# 花式索引是指使用整数数组（或布尔数组）来索引数组，从而一次获取多个元素。
    t_batch=t_train[batch_mask]
    # 4.2计算梯度
    # 相对于非反向传播就改了这里！@！！
    #grad=network.numerical_gradient(x_batch,t_batch)
    grad=network.gradient(x_batch,t_batch)
    # 4.3变更参数
    for key in ('W1',"W2",'b1','b2'):
        network.params[key]-=learning_rate*grad[key]
    # 4.4计算并保存当前的训练损失
    loss=network.loss(x_batch,t_batch)
    train_loss_list.append(loss)
    # 4.5每完成一个epoch的迭代，就计算并保存训练准确率
    if i%iter_per_epoch==0: # i是总迭代次数
        train_acc=network.accuracy(x_train,t_train)
        test_acc=network.accuracy(x_test,t_test)
        train_acc_list.append(train_acc)
        test_acc_list.append(test_acc)
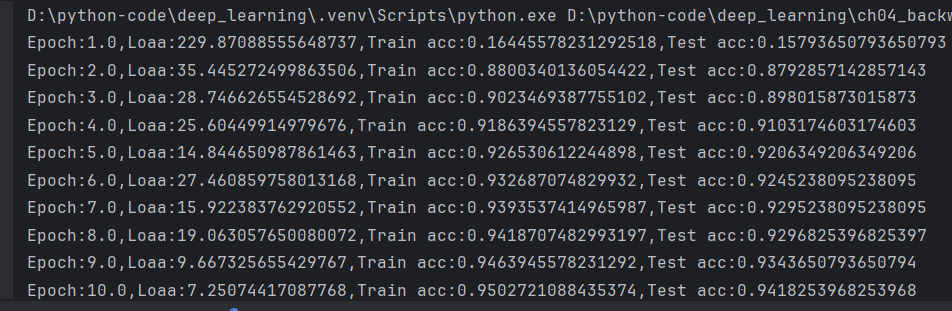
        print('Epoch:{},Loaa:{},Train acc:{},Test acc:{}'.format(i//iter_per_epoch+1,loss,train_acc,test_acc))
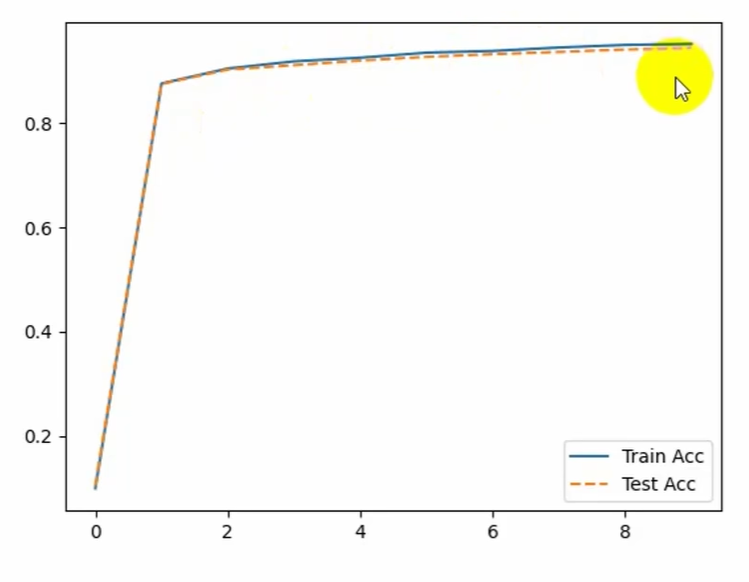
# 5.画图
x=np.arange(len(train_acc_list))
plt.plot(x,train_acc_list,label="Train acc")
plt.plot(x,test_acc_list,label="Test acc",linestyle='--')
plt.legend(loc='best')
plt.show()

运行结果：

相关推荐
水如烟2 小时前
孤能子视角:数字时代的“众“与“独“，“三观“––守护自身“本真性“
人工智能
小熊熊知识库2 小时前
Pytorch介绍以及AI模型 window 安装下载详解
人工智能·pytorch·python
AndrewHZ2 小时前
【图像处理基石】图像处理领域还有哪些核心挑战与难题？
图像处理·人工智能·算法·计算机视觉·噪声·图像增强·画质增强
极客范儿2 小时前
从快手“12·22”事故出发：AI时代，如何构建对抗自动化攻击的动态免疫体系？
网络·人工智能·自动化
啊阿狸不会拉杆2 小时前
《数字图像处理》实验8-图像识别与分类
图像处理·人工智能·算法·分类·数据挖掘·数字图像处理
core5122 小时前
XGBoost：机器学习界的“速度与激情”
机器学习·xgboost
科技快报2 小时前
联想现场演示天禧AI 3.5多模态交互，YOGA Pro 16 Aura AI元启版提供坚实算力支撑
人工智能·microsoft
week_泽2 小时前
opencv特征检测、关键点、角点检测、特征点检测
人工智能·opencv·计算机视觉
月明长歌2 小时前
【码道初阶】Leetcode138：随机链表的复制：用 HashMap 做深拷贝的标准解法
java·数据结构·算法·leetcode·链表·哈希算法
热门推荐
01从快手“12·22”直播攻击事件看：一次教科书式的业务层饱和攻击02GitHub 镜像站点033D 圣诞树网页代码04Linux下V2Ray安装配置指南05UV安装并设置国内源06在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）07电脑检测软件—图吧工具箱08Gemini3 生成的基于手势控制3D粒子圣诞树09jdk21下载、安装（Windows、Linux、macOS）102025 最新教程：注册并切换到美区 Apple ID