记数排序（基数排序和桶排序）

1、记数排序

概念：

简述：将整个数组中的各个数据的个数数出来，然后讲这些数据重新填入原数组中

将要排序的数组先遍历一遍，选出最大的和最小的，以max-min+1(左闭右闭区间)为范围range

cpp 复制代码

int min = arr[0], max = arr[0];
	//这里很巧妙，以arr[0]作为min和max，可以解决排序负数的问题
	for (int i = 0; i < n; i++)
	{
		if (arr[i] > max)
			max = arr[i];
		if (arr[i] < min)
			min = arr[i];
	}

以range为数组大小开一个数组count，将数组中的数据全都初始化为0,

这里存在一个问题：我们难道要将0到max的值全部开出来吗

答：不是，我们采用"相对值"的方法（即将数据储存在相对于最小值的位置）

cpp 复制代码

int range = max - min + 1;
	int* count = (int*)calloc(range, sizeof(int));
	//nullptr判断
	if (nullptr == count)
	{
		perror("calloc fail");
	}

我们再将原数组中的数据中的每个数据的个数统计出来

cpp 复制代码

for (int i = 0; i < n; i++)
	{
		count[arr[i] - min]++;
	}

然后将count中的数依次填入原数组

cpp 复制代码

int j = 0;
	for (int i = 0; i < range; i++)
	{
		while (count[i]-- > 0)
		{
			arr[j++] = i + min;
		}
	}

实现：

cpp 复制代码

void CountSort(int* arr, int n)
{
	int min = arr[0], max = arr[0];
	//这里很巧妙，以arr[0]作为min和max，可以解决排序负数的问题
	for (int i = 0; i < n; i++)
	{
		if (arr[i] > max)
			max = arr[i];
		if (arr[i] < min)
			min = arr[i];
	}
	int range = max - min + 1;
	int* count = (int*)calloc(range, sizeof(int));
	if (nullptr == count)
	{
		perror("calloc fail");
		return;
	}
	for (int i = 0; i < n; i++)
	{
		count[arr[i] - min]++;
	}

	int j = 0;
	for (int i = 0; i < range; i++)
	{
		while (count[i]-- > 0)
		{
			arr[j++] = i + min;
		}
	}
}

分析：

时间复杂度：O(N+range)

空间复杂度：O(range)

这使得记数排序适合排序数的大小范围较集中的数据

（当然，数据量足够大的时候这个方面的影响会减弱）

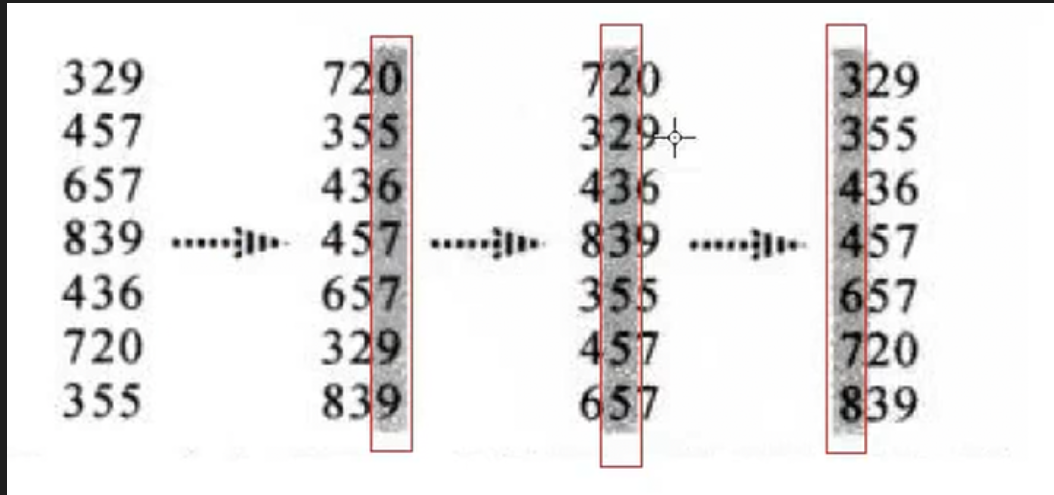
2、基数排序

太废了，不做进一步了解

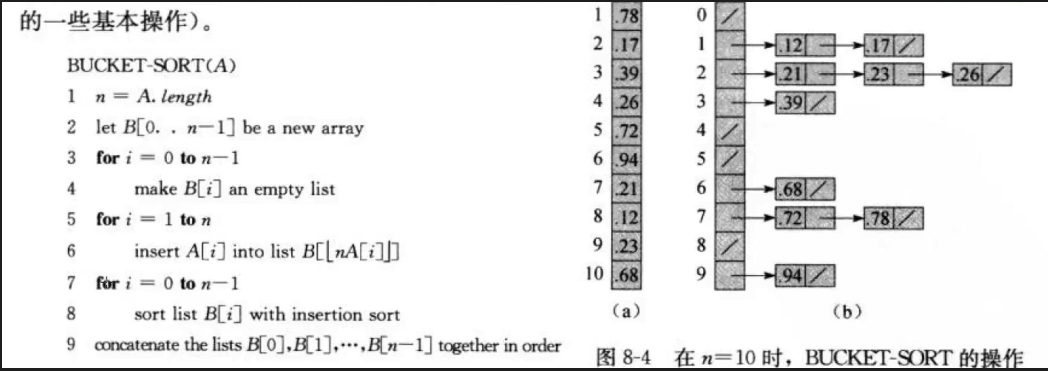
3、桶排序

太废了，不做进一步了解

在这里插入图片描述