1.子数组/子串是连续的 子序列不一定是连续的 abcde中ace就是子序列
2.给定两个字符串,求两个的最长公共子序列,dfs(i,j)定义:序列1的前i个字母和序列2的前j个字母 的最长公共子序列
下一个问题:序列1前i-1个字母和序列二前j-1个字母
序列1前i个字母和序列二前j-1个字母
序列1前i-1个字母和序列二前j个字母
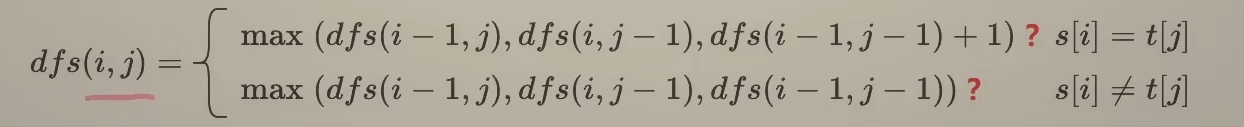
可以简化:
dfs(i,j) = dfs(i-1,j-1)+1 s[i]=t[j]
dfs(i,j) = max(dfs(i-1,j),dfs(i,j-1)) s[i]≠t[j]
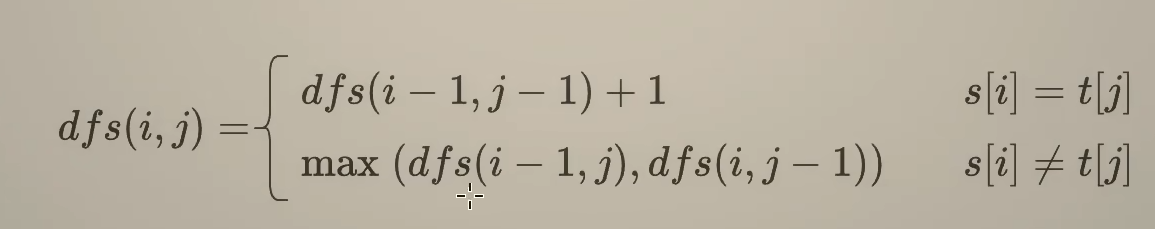
最长公共子序列
1.回溯法
时间复杂度 nm 空间复杂度 nm
class Solution:
def longestCommonSubsequence(self, text1: str, text2: str) -> int:
n = len(text1)
m = len(text2)
@cache
def dfs(i,j):
if i<0 or j<0:
return 0
if text1[i]==text2[j]:
return dfs(i-1,j-1)+1
else:
return max(dfs(i-1,j),dfs(i,j-1))
return dfs(n-1,m-1)2.递推
先得到递推公式
f[i][j] = f[i-1][j-1]+1 s[i]=t[j]
max(f[i-1][j],f[i][j-1] s[i]≠t[j]
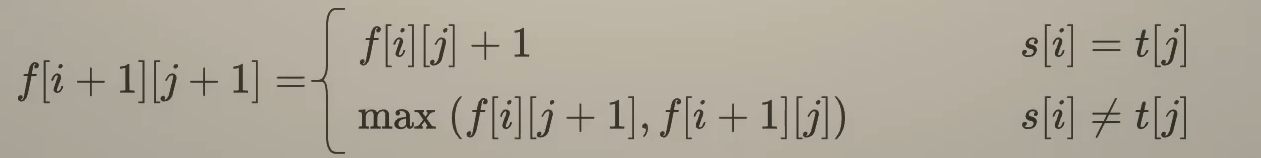
f = [[0]*(m+1)for _ in range(n+1)]
for i,x in enumerate(text1):
for j,y in enumerate(text2):
if x==y:
f[i+1][j+1] = f[i][j]+1
else:
f[i+1][j+1] = max(f[i][j+1],f[i+1][j])
return f[n][m]3.空间优化
可以发现更新f[i+1][j+1]需要三个值,左边,上面,左上,但左上的数据会被覆盖,引入pre变量
pre = f[0] 不能写在循环外面,核心原因是:进入 j 循环后,pre 会逐步保存「上一个 j 位置的旧值」,精准匹配二维 DP 中dp[i-1][j-1]的语义。
空间复杂度 m
f = [0]*(m+1)
for i,x in enumerate(text1):
pre = f[0]
for j,y in enumerate(text2):
tmp = f[j+1]
if x==y:
f[j+1] = pre+1
else:
f[j+1] = max(f[j+1],f[j])
pre = tmp
return f[m]编辑距离
为什么叫编辑距离:
"编辑":指对字符串的修改操作(插入、删除、替换是文本编辑中最基础的三种操作)
距离: 操作次数越少,差异越小,距离越近
dfs(i, j)的定义 表示将 s[0..i](s 的前 i+1 个字符)转换为 t[0..j](t 的前 j+1 个字符)所需的最少操作数。
dfs(i-1, j) + 1 → 对应「删除操作」
含义:先将 s[0..i-1] 转换为 t[0..j](操作数是 dfs(i-1, j)),再删除 s[i](+1 次操作)
dfs(i, j-1) + 1 → 对应「插入操作」
- 含义:先将
s[0..i]转换为t[0..j-1](操作数是dfs(i, j-1)),再插入t[j]到 s 中(+1 次操作)。
dfs(i-1, j-1) + 1 → 对应「替换操作」
含义:先将 s[0..i-1] 转换为 t[0..j-1](操作数是 dfs(i-1, j-1)),再将 s[i] 替换为 t[j](+1 次操作)
而如果 s[i] == t[j],则不需要任何操作,直接继承 dfs(i-1, j-1) 的结果(这是 "无操作" 的情况)。
1.回溯法
1.回溯公式:
dfs(i,j) = dfs(i-1,j-1) if s[i] == t[j]
dfs(i,j) = min(dfs(i,j-1),dfs(i-1,j),dfs(i-1,j-1)) +1 if s[i] ≠ t[j]
插入 删除 替换
2.边界条件:if i<0:return j+1 把j全加一遍,就相同了
if j<0:return i+1 把i全删了,就相同了
class Solution:
def minDistance(self, word1: str, word2: str) -> int:
n = len(word1)
m = len(word2)
@cache
def dfs(i,j):
if i<0:return j+1
if j<0:return i+1
if word1[i]==word2[j]:
return dfs(i-1,j-1)
else:
return min(dfs(i,j-1),dfs(i-1,j),dfs(i-1,j-1))+1
return dfs(n-1,m-1)2.递推:
我卡住的地方:
if i<0:return j+1
if j<0:return i+1 怎么转换到二维数组里
首先 dfs 的定义是将 text1 前 i 转换为 text2 前 j 最少需要的操作次数
DP 的f[0][j]:对应递归的i=-1,此时 DP 的j对应递归的j-1 → 应返回(j-1)+1 = j(而非j+1)
综上:i<0 对应的是 f[0][j] 数组的第一行 j+1 在这是 j
j<0对应的是 f[i][0]数组的第一列 i+1在这是i
所以边界条件:
for j in range(m+1):
f[0][j] = j
for i in range(n+1):
f[i][0] = i
f = [[0]*(m+1)for _ in range(n+1)]
for j in range(m+1):
f[0][j] = j
for i in range(n+1):
f[i][0] = i
for i,x in enumerate(word1):
for j,y in enumerate(word2):
if x==y:
f[i+1][j+1] = f[i][j]
else:
f[i+1][j+1] = min(f[i+1][j],f[i][j+1],f[i][j])+1
return f[n][m]3.空间优化
和最长公子序列不同的是,这个题的二维数组的第一行和第一列是动态的,而最长公子序列的第一行和第一列都是0,所以这个题要考虑的更多
1.一维数组的创建:
f = [j for j in range(m+1)] 并不是简单的创了一个全是0 的数组
2.pre = f[0] f[0] = i+1 pre记录旧值,f[0] = i+1对应的是
dfs的 for i in range(n+1):
f[i][0] = i的操作
综合起来达到动态的f[0]的效果
f = [j for j in range(m+1)]
for i,x in enumerate(word1):
pre = f[0]
f[0] = i+1
for j,y in enumerate(word2):
temp = f[j+1]
if x==y:
f[j+1] = pre
else:
f[j+1] = min(f[j],f[j+1],pre) +1
pre=temp
return f[m]最长递增子序列
1.回溯法:
若用常见的选或不选思路进行回溯,会递归遍历所有可能的子序列,比如数组长度为 n 时,子序列总数是 2ⁿ
修改思路,dfs(i)专注于 "以 i 结尾" 的子序列长度
外部遍历所有i,是为了覆盖 "以任意元素结尾" 的所有可能,从而得到全局最长长度。
此时dfs(i)的定义:以nums[i]结尾的最长递增子序列长度
外边再遍历一遍所有结尾情况,就能得出答案了
回溯公式:
dfs(i) = max {dfs(j)} +1 j<i and nums[j]<nums[i]
回溯代码:
def dfs(i):
temp = 0
for j in range(i):
if nums[j] < nums[i]:
temp = max(temp,dfs[j])
return temp+1
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
n = len(nums)
ans = 0
@cache
def dfs(i):
temp=0
for j in range(i):
if nums[j]<nums[i]:
temp = max(temp,dfs(j))
return temp+1
for i in range(n):
ans = max(ans,dfs(i))
return ans2.递推
递推公式:
f[i] = max{f(j)} +1 j<i and nums[j]<nums[i]
f = [0]*n
for i in range(n):
for j in range(i):
if nums[j]<nums[i]:
f[i] = max(f[i],f[j])
f[i] += 1
return max(f)