Evaluation of Clutter Suppression in CP-OFDM-Based Passive Radar (II)

文章目录

- [IV. EVALUATION OF CLUTTER SUPPRESSION](#IV. EVALUATION OF CLUTTER SUPPRESSION)
- - [A. Relationship Among Three Algorithms](#A. Relationship Among Three Algorithms)
  - [B. Clutter Suppression Performance](#B. Clutter Suppression Performance)
  - [C. Doppler Response](#C. Doppler Response)

IV. EVALUATION OF CLUTTER SUPPRESSION

在第三节中，我们简要介绍了三种子载波域杂波抑制算法。事实上，由于这些算法都在子载波域运行，它们之间可能存在内在联系。在本节中，我们将探讨这三种算法之间的关系，并比较它们的杂波抑制性能和多普勒响应。为了进行比较，我们引入了一种有效的时域方法，即广义子带对消 (generalized subband cancelation，GSC) [32]，作为基准。

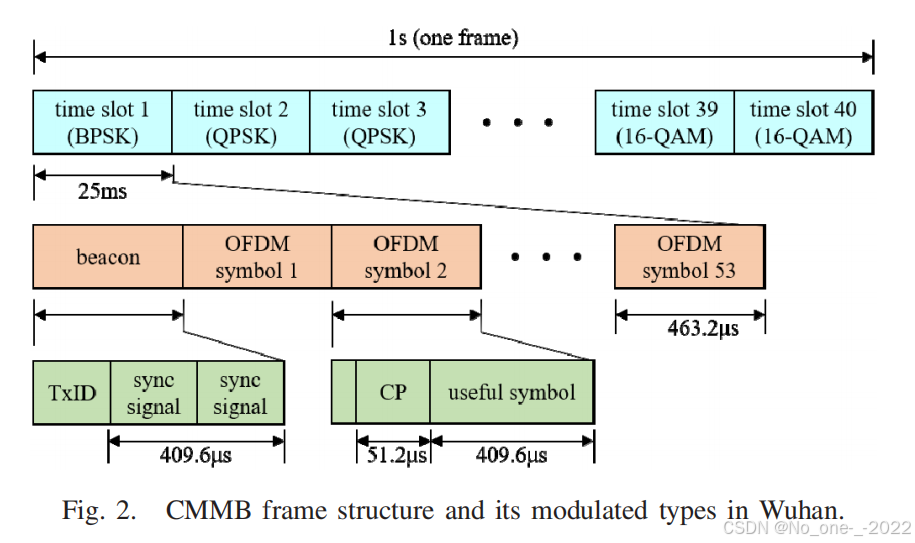
为了更直观地评估这些算法，我们在本节中考虑一个仿真场景。在仿真中，假设模拟参考信号是根据典型的 CP-OFDM 波形参数生成的，即 CMMB 信号。图 2 [16] 展示了中国武汉市的 CMMB 帧结构及其调制类型。具体而言，

一帧 CMMB 信号持续 1 s 1\text{ s} 1 s，包含 40 个时隙。
第一个时隙基于 BPSK 调制映射，
最后两个时隙基于 16-QAM 调制映射。
其他时隙均基于 QPSK 调制映射。
每个时隙由一个信标和 53 个 OFDM 符号组成。
此外，信标可分为一个发射机识别信号 (TxID) 和两个相同的同步 (sync) 信号。
OFDM 符号的主体由有用符号 ( T u = 409.6 μ s T_u = 409.6\mu s Tu=409.6μs) 和循环前缀 ( T g = 51.2 μ s T_g = 51.2\mu s Tg=51.2μs) 组成。

为简单起见，我们在仿真中忽略信标，仅使用 CMMB 中的 CP 和有用符号参数。模拟信号的生成过程如下：首先，模拟随机数据流，然后对数据流执行 IDFT 以形成 OFDM 符号。最后，模拟参考信号由这些带有 CP 的 OFDM 符号组成。此外，与一个 CMMB 帧中的多种调制类型不同，我们在模拟参考信号中仅采用一种调制类型，如 QPSK 或 16-QAM。在这种情况下，积分时长由 1696 个连续的 OFDM 符号组成，这些符号在 10 MHz 10\text{ MHz} 10 MHz 的采样率下采用 QPSK 或 16-QAM 调制，从而产生约 68.4 dB 68.4\text{ dB} 68.4 dB 的积分增益。

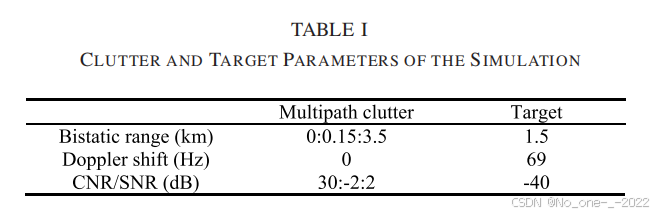
仿真参数的值列于表 I 中。在监测通道中，使用 15 个静止散射体来模拟杂波。杂波的杂噪比 (CNR) 取值为 ( 30 : − 2 : 2 ) dB (30:-2:2)\text{ dB} (30:−2:2) dB，其中 ( 30 : − 2 : 2 ) (30:-2:2) (30:−2:2) 表示从 30 到 2、步长为 -2 的序列。对应的双基地距离为 ( 0 : 0.15 : 3.5 ) km (0:0.15:3.5)\text{ km} (0:0.15:3.5) km。此外，在双基地距离 1.5 km 1.5\text{ km} 1.5 km 和多普勒频移 69 Hz 69\text{ Hz} 69 Hz 附近合成了一个信噪比 (SNR) 为 − 40 dB -40\text{ dB} −40 dB 的目标。此外，热噪声被建模为复高斯白噪声。

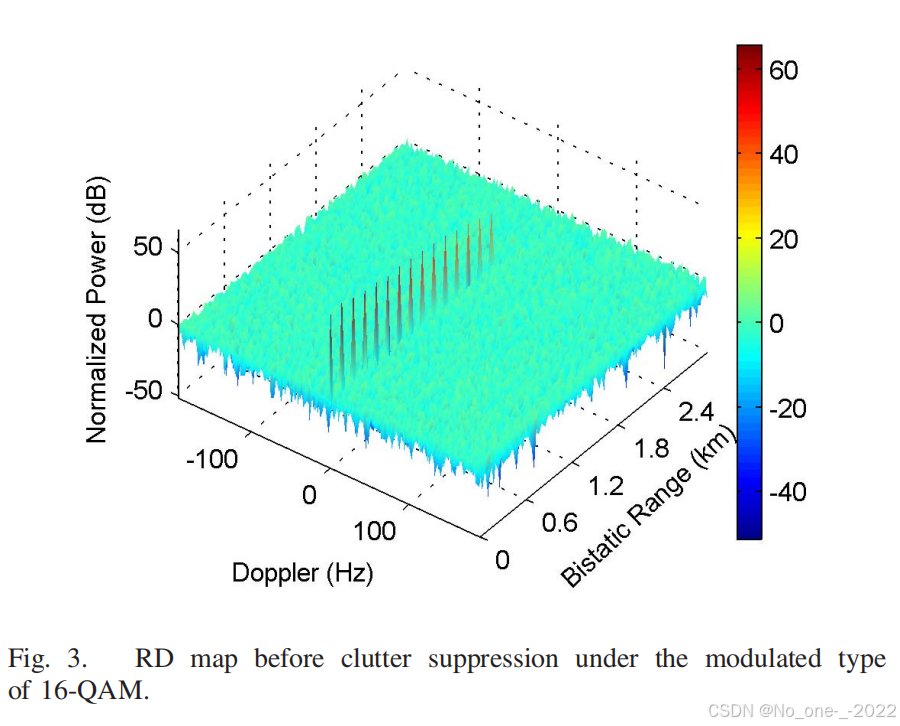
为了突显杂波抑制的重要性，图 3 给出了在 16-QAM 调制类型下杂波抑制前的距离-多普勒 (RD) 图。该图是基于 2-D DFT 方法并在 OFDM 符号上进行脉冲压缩获得的。从图 3 中我们可以看到，在没有任何对消或缓解效果之前，模拟杂波存在于零频率处，且目标被杂波旁瓣掩盖，这表明了在基于 CP-OFDM 的无源雷达中进行杂波抑制的必要性。

文中提到的 "2-D DFT approach" 通常指的是一种基于 FFT 的快速互模糊函数（CAF）计算方法（类似 FMCW 或 Batch 处理算法）。这里的"脉冲压缩"并不是在时域做卷积，而是在频域（子载波域） 实现的。请参考文中公式 (14)： χ [ m , p ] = ∑ l = 0 L − 1 e − j 2 π p l / L ∑ k = 0 N u − 1 Y l , k C l , k ∗ e j 2 π N u k m ⏟ 距离维处理 (脉冲压缩) \chi[m,p] = \sum_{l=0}^{L-1} e^{-j2\pi pl/L} \underbrace{\sum_{k=0}^{N_u-1} Y_{l,k} C_{l,k}^* e^{j\frac{2\pi}{N_u}km}}_{\text{距离维处理 (脉冲压缩)}} χ[m,p]=l=0∑L−1e−j2πpl/L距离维处理 (脉冲压缩) k=0∑Nu−1Yl,kCl,k∗ejNu2πkm

Y l , k C l , k ∗ Y_{l,k} C_{l,k}^* Yl,kCl,k∗：这一步即为频域匹配滤波。将接收到的子载波数据 Y l , k Y_{l,k} Yl,k 与参考信号的共轭 C l , k ∗ C_{l,k}^* Cl,k∗ 相乘。这在数学上等价于时域的互相关（即脉冲压缩）。

∑ k = 0 N u − 1 ( ... ) e j ... \sum_{k=0}^{N_u-1} (\dots) e^{j\dots} ∑k=0Nu−1(...)ej...：这是一个 IDFT 过程。它将频域的点乘结果变换回时域（距离门 m m m），从而完成脉冲压缩，形成尖锐的距离峰值。

A. Relationship Among Three Algorithms

根据著名的正交投影定理，我们可以将 (22) 中的矩阵 C k ( C k H C k ) − 1 C k H \boldsymbol{C}_k(\boldsymbol{C}_k^H \boldsymbol{C}_k)^{-1}\boldsymbol{C}_k^H Ck(CkHCk)−1CkH 视为正交投影矩阵。但我们也可以将标量 ( C k H C k ) − 1 C k H Y k (\boldsymbol{C}_k^H \boldsymbol{C}_k)^{-1}\boldsymbol{C}_k^H \boldsymbol{Y}_k (CkHCk)−1CkHYk 视为通过最小二乘 (LS) 准则估计的第 k k k 个子载波的信道响应。即

H ^ k = ( C k H C k ) − 1 C k H Y k (25) \hat{H}_k = (\boldsymbol{C}_k^H \boldsymbol{C}_k)^{-1}\boldsymbol{C}_k^H \boldsymbol{Y}_k \tag{25} H^k=(CkHCk)−1CkHYk(25)

然后我们将 (25) 分解为两部分：

( C k H C k ) − 1 = ( ∑ l = 0 L − 1 ∣ C l , k ∣ 2 ) − 1 (26) (\boldsymbol{C}k^H \boldsymbol{C}k)^{-1} = \left(\sum{l=0}^{L-1} |C{l,k}|^2 \right)^{-1} \tag{26} (CkHCk)−1=(l=0∑L−1∣Cl,k∣2)−1(26)

以及

C k H Y k = C k H ( H k C k + γ k Λ f d 0 C k + N k ) = ∑ l = 0 L − 1 H l , k ∣ C l , k ∣ 2 + γ k ∑ l = 0 L − 1 e j 2 π f D , 0 l T e ∣ C l , k ∣ 2 + C k H N k (27) \begin{aligned} \boldsymbol{C}k^H \boldsymbol{Y}k &= \boldsymbol{C}k^H (\boldsymbol{H}k \boldsymbol{C}k + \gamma_k \boldsymbol{\Lambda}{f_d^0} \boldsymbol{C}k + \boldsymbol{N}k) \\ &= \sum{l=0}^{L-1} H{l,k} |C{l,k}|^2 + \gamma_k \sum{l=0}^{L-1} e^{j2\pi f{D,0} l T_e} |C{l,k}|^2 + \boldsymbol{C}_k^H \boldsymbol{N}_k \end{aligned} \tag{27} CkHYk=CkH(HkCk+γkΛfd0Ck+Nk)=l=0∑L−1Hl,k∣Cl,k∣2+γkl=0∑L−1ej2πfD,0lTe∣Cl,k∣2+CkHNk(27)

现在，(25) 可以重写为

H ^ k = ∑ l = 0 L − 1 H l , k ∣ C l , k ∣ 2 ∑ l = 0 L − 1 ∣ C l , k ∣ 2 + γ k ∑ l = 0 L − 1 e j 2 π f D , 0 l T e ∣ C l , k ∣ 2 ∑ l = 0 L − 1 ∣ C l , k ∣ 2 + C k H N k ∑ l = 0 L − 1 ∣ C l , k ∣ 2 (28) \hat{H}k = \frac{\sum{l=0}^{L-1} H_{l,k} |C_{l,k}|^2}{\sum_{l=0}^{L-1} |C_{l,k}|^2} + \gamma_k \frac{\sum_{l=0}^{L-1} e^{j2\pi f_{D,0} l T_e} |C_{l,k}|^2}{\sum_{l=0}^{L-1} |C_{l,k}|^2} + \frac{\boldsymbol{C}k^H \boldsymbol{N}k}{\sum{l=0}^{L-1} |C{l,k}|^2} \tag{28} H^k=∑l=0L−1∣Cl,k∣2∑l=0L−1Hl,k∣Cl,k∣2+γk∑l=0L−1∣Cl,k∣2∑l=0L−1ej2πfD,0lTe∣Cl,k∣2+∑l=0L−1∣Cl,k∣2CkHNk(28)

如第 III-C 节所述，本文基于星座图定义了两种 OFDM 信号调制方案，即等模调制方案和非等模调制方案。它们分别代表等模和非等模星座映射。

CASE 1：OFDM 符号采用等模调制（例如 QPSK）。 在这种情况下，我们要么有 ∣ C l , k ∣ 2 = 1 |C_{l,k}|^2 = 1 ∣Cl,k∣2=1 。方程 (28) 可以简化为
H ^ k = 1 L ∑ l = 0 L − 1 ( H l , k + γ k e j 2 π f D , 0 l T e + N l , k C l , k ) ≈ 1 L ∑ l = 0 L − 1 H l , k (29) \hat{H}k = \frac{1}{L} \sum{l=0}^{L-1} \left( H_{l,k} + \gamma_k e^{j2\pi f_{D,0} l T_e} + \frac{N_{l,k}}{C_{l,k}} \right) \approx \frac{1}{L} \sum_{l=0}^{L-1} H_{l,k} \tag{29} H^k=L1l=0∑L−1(Hl,k+γkej2πfD,0lTe+Cl,kNl,k)≈L1l=0∑L−1Hl,k(29)
将上述方程与 (16) 和 (18) 进行比较，我们可以看到这三个方程是一致的。这表明 ACRF-C 和 ECA-C 方法的杂波抑制机制在等模调制方案中是完全等效的。
CASE 2：OFDM 符号采用非等模调制（例如 16-QAM）。 在这种情况下，调制数据 C l , k C_{l,k} Cl,k 的模值随星座映射而变化。然而，在这种类型的调制方案中，通常会有一个特定的缩放因子与星座映射操作相关联，以将所有符号的平均能量归一化为 1。即
E { ∣ C l , k ∣ 2 } ≈ 1 L ∑ l = 0 L − 1 ∣ C l , k ∣ 2 ≈ 1 (30) E\left\{ |C_{l,k}|^2 \right\} \approx \frac{1}{L} \sum_{l=0}^{L-1} |C_{l,k}|^2 \approx 1 \tag{30} E{∣Cl,k∣2}≈L1l=0∑L−1∣Cl,k∣2≈1(30)
在块衰落信道的假设下，即 H 0 , k ≈ ⋯ ≈ H L − 1 , k = H k H_{0,k} \approx \cdots \approx H_{L-1,k} = H_k H0,k≈⋯≈HL−1,k=Hk，(28) 中的第一项可以写为
∑ l = 0 L − 1 H l , k ∣ C l , k ∣ 2 ∑ l = 0 L − 1 ∣ C l , k ∣ 2 = H k ∑ l = 0 L − 1 ∣ C l , k ∣ 2 ∑ l = 0 L − 1 ∣ C l , k ∣ 2 = H k = 1 L ∑ l = 0 L − 1 H l , k (31) \frac{\sum_{l=0}^{L-1} H_{l,k} |C_{l,k}|^2}{\sum_{l=0}^{L-1} |C_{l,k}|^2} = H_k \frac{\sum_{l=0}^{L-1} |C_{l,k}|^2}{\sum_{l=0}^{L-1} |C_{l,k}|^2} = H_k = \frac{1}{L} \sum_{l=0}^{L-1} H_{l,k} \tag{31} ∑l=0L−1∣Cl,k∣2∑l=0L−1Hl,k∣Cl,k∣2=Hk∑l=0L−1∣Cl,k∣2∑l=0L−1∣Cl,k∣2=Hk=L1l=0∑L−1Hl,k(31)
同样，对于 (28) 中的第二项，我们有
γ k ∑ l = 0 L − 1 e j 2 π f D , 0 l T e ∣ C l , k ∣ 2 ∑ l = 0 L − 1 ∣ C l , k ∣ 2 ≈ γ k L ∑ l = 0 L − 1 e j 2 π f D , 0 l T e ∣ C l , k ∣ 2 ≈ 0 (32) \gamma_k \frac{\sum_{l=0}^{L-1} e^{j2\pi f_{D,0} l T_e} |C_{l,k}|^2}{\sum_{l=0}^{L-1} |C_{l,k}|^2} \approx \frac{\gamma_k}{L} \sum_{l=0}^{L-1} e^{j2\pi f_{D,0} l T_e} |C_{l,k}|^2 \approx 0 \tag{32} γk∑l=0L−1∣Cl,k∣2∑l=0L−1ej2πfD,0lTe∣Cl,k∣2≈Lγkl=0∑L−1ej2πfD,0lTe∣Cl,k∣2≈0(32)
现在，忽略热噪声的影响，(28) 可以最终简化为
H ^ k ≈ 1 L ∑ l = 0 L − 1 H l , k (33) \hat{H}k \approx \frac{1}{L} \sum{l=0}^{L-1} H_{l,k} \tag{33} H^k≈L1l=0∑L−1Hl,k(33)

虽然 (33) 中 H ^ k \hat{H}_k H^k 的表达式与 (18) 中的相同，但在非等模调制方案的情况下，ACRF-C 和 ECA-C 方法并不完全等效。

根据 (31)，在 ECA-C 方法中，通过 LS 准则获得的杂波信道频率响应估计是最小方差无偏 (the minimum variance unbiased (MVU)
estimation) 估计 [33]，因为考虑了子载波模值的权重。
相比之下，ACRF-C 仅仅是对杂波信道频率响应做出了渐近无偏估计（make an asymptotically unbiased estimation），如 (16) 所示。

因此，ECA-C 方法可以比 ACRF-C 获得更可靠的信道信息。这种差异将通过数值模拟和实验数据反映在 RD 图中。在非等模调制方案中，ECA-C 在零多普勒处具有比 ACRF-C 更深的零陷。

现在，我们可以部分得出结论：在等模调制方案中，ACRF-C 和 ECA-C 方法的杂波抑制机制是完全等效的；而在非等模调制方案中，它们是统计等效的。

在上述两种算法中，参考信号和监测信号在进行抑制操作之前都已被分解为 OFDM 块。为了充分利用 OFDM 块并保持信号处理的连续性，杂波抑制后的互模糊函数 (CAF) 计算也是基于 OFDM 块进行的。正如我们所见，这两种算法的目的是去除包含在 CAF 中的杂波分量，即 χ c [ m , p ] \chi_c[m, p] χc[m,p]。

但在第 III-C 小节中，我们已经指出，RSD 方法可以将 RD 图中所有静止杂波的能量集中在零多普勒处，从而在零多普勒线之外没有旁瓣。换句话说，虽然 ACRF-C 和 ECA-C 算法可以抑制监测通道中的杂波，但在旁瓣抑制方面的目标检测上，它们似乎没有优势。

ACRF-C / ECA-C：试图让杂波 Amplitude → 0 \text{Amplitude} \to 0 Amplitude→0。如果没减干净，剩下的杂波依然像原始信号一样，有由于波形相关性导致的旁瓣扩散。

RSD：通过数学变换（ C ⋅ 1 / C = 1 C \cdot 1/C = 1 C⋅1/C=1），让杂波的旁瓣结构直接消失。无论杂波多强，它在多普勒维上都不扩散。

为了验证上述理论分析，图 4 和图 5 分别展示了遵循表 I 中仿真参数的 QPSK 和 16-QAM 调制类型下的仿真结果。这些图是通过按目标功率缩放数据并将最小值截断至 − 60 dB -60\text{ dB} −60 dB 的水平获得的。

图 4(a) 和图 5(a) 分别显示了在上述两种调制类型下，由 ACRF-C、ECA-C、RSD 和时域方法 GSC 获得的 RD 图。为了节省空间，这四种方法获得的 RD 图都被放置在同一张图中，并由间隙隔开。标有方法名称的水平轴代表多普勒频率，垂直轴代表双基地距离。与图 3 中杂波抑制前的 RD 图相比，每种算法都能在两种调制方案中成功检测到目标。不同之处在于，

对于 QPSK，ACRF-C 和 ECA-C 方法都能产生很深的零多普勒零陷，
但对于 16-QAM，只有 ECA-C 方法具有相当深的零陷。这一结果与理论预测一致，因为 ECA-C 获得的估计信道响应是 MVU 估计。

图 4(b) 和图 5(b) 展示了四种算法杂波抑制后的归一化目标距离单元截面图。可以注意到，

对于 QPSK，三种子载波域算法表现出相同的目标检测性能，并且与时域方法 GSC 相当。即使对于非等模调制方案，尽管 ECA-C 在零多普勒处产生更深的零陷，ACRF-C 获得的目标检测性能也几乎与 ECA-C 相同。
与等模调制方案不同，非等模调制方案中的均衡操作使得 RSD 与其他两种子载波域算法略有不同，这将在第 IV-B 小节中进行理论分析。此外，与时域方法相比，子载波域算法在非等模调制方案中仍能保持相当的目标检测性能。

总之，三种子载波域算法之间存在密切联系。即：

在等模调制方案中，三种子载波域算法可以获得相同的目标检测性能。
在非等模调制方案中，RSD 方法在目标检测性能方面与其他两种子载波域算法略有不同。此外，ECA-C 方法产生的更深零陷并没有显着提高目标检测性能。
在任何类型的调制方案中，子载波域算法在仿真场景下都能达到与时域算法相当的目标检测性能。

B. Clutter Suppression Performance

在本小节中，我们对杂波抑制性能进行数学分析。有多种指标可用于衡量杂波抑制性能 [27]。本文选择杂波抑制后 RD 图中的目标信噪比 (SNR) 作为衡量指标。即

S N R t a r ( χ ) = E { ∣ χ [ m 0 , p 0 ] ∣ 2 } E { ∑ m ∈ T , p ∈ F ∣ χ [ m , p ] ∣ 2 } , (34) SNR_{tar}(\chi) = \frac{E\{|\chi[m_0, p_0]|^2\}}{E\{\sum_{m\in T, p\in F} |\chi[m, p]|^2\}}, \tag{34} SNRtar(χ)=E{∑m∈T,p∈F∣χ[m,p]∣2}E{∣χ[m0,p0]∣2},(34)

其中 m 0 m_0 m0 和 p 0 p_0 p0 分别是目标的距离单元和多普勒单元。参数 T T T 和 F F F 定义了 RD 图中特定区域的距离单元和多普勒单元集合，该区域不包含目标响应和主要杂波分量。我们使用 E { ∑ m ∈ T , p ∈ F ∣ χ [ m , p ] ∣ 2 } E\{\sum_{m\in T,p\in F} |\chi[m, p]|^2\} E{∑m∈T,p∈F∣χ[m,p]∣2} 来估计噪声基底的平均水平。

由于 ACRF-C 背后的原理与 ECA-C 方法几乎相同，因此本小节我们只需研究 ECA-C 和 RSD 的抑制性能。

ECA-C： 经 ECA-C 杂波抑制后的互模糊函数 (CAF) 可近似表示为
χ ~ [ m , p ] ≈ χ t a r [ m , p ] + χ n [ m , p ] , (35) \tilde{\chi}[m, p] \approx \chi_{tar}[m, p] + \chi_n[m, p], \tag{35} χ~[m,p]≈χtar[m,p]+χn[m,p],(35)

公式 (35) 的近似号 ≈ \approx ≈ 隐含了以下假设：杂波被完全抑制：

ECA-C 有效地移除了所有与参考信号相关的静态干扰。

目标未被误伤：假设目标具有一定的多普勒速度，使其未被当作杂波滤除（即目标信号不在杂波子空间内）。

其中 χ t a r [ m , p ] \chi_{tar}[m, p] χtar[m,p] 和 χ n [ m , p ] \chi_n[m, p] χn[m,p] 在 (15) 中定义。通常，假设两个独立的随机变量 C l , k C_{l,k} Cl,k 和 N l , k N_{l,k} Nl,k 是独立同分布 (i.i.d) 序列。这表明目标回波与高斯白噪声互不相关。将 (35) 中的 [ m , p ] [m, p] [m,p] 替换为 [ n 0 , p 0 ] [n_0, p_0] [n0,p0] 并遵循 E { ∣ C l , k ∣ 2 } = 1 E\{|C_{l,k}|^2\} = 1 E{∣Cl,k∣2}=1 的条件，可以得到目标峰值的平均电平如下

E { ∣ χ ~ [ n 0 , p 0 ] ∣ 2 } = E { ∣ χ t a r [ n 0 , p 0 ] ∣ 2 } + E { ∣ χ n [ n 0 , p 0 ] ∣ 2 } ≈ E { ∣ χ t a r [ n 0 , p 0 ] ∣ 2 } = ∑ l = 0 L − 1 ∑ k = 0 N u − 1 ∣ a 0 ∣ 2 E { ∣ C l , k ∣ 2 } = L 2 N u 2 ∣ a 0 ∣ 2 , (36) \begin{aligned} E\{|\tilde{\chi}[n_0, p_0]|^2\} &= E\{|\chi_{tar}[n_0, p_0]|^2\} + E\{|\chi_n[n_0, p_0]|^2\} \\ &\approx E\{|\chi_{tar}[n_0, p_0]|^2\} \\ &= \sum_{l=0}^{L-1} \sum_{k=0}^{N_u-1} |a_0|^2 E\left\{|C_{l,k}|^2\right\} \\ &= L^2 N_u^2 |a_0|^2, \end{aligned} \tag{36} E{∣χ~[n0,p0]∣2}=E{∣χtar[n0,p0]∣2}+E{∣χn[n0,p0]∣2}≈E{∣χtar[n0,p0]∣2}=l=0∑L−1k=0∑Nu−1∣a0∣2E{∣Cl,k∣2}=L2Nu2∣a0∣2,(36)

其中 L L L 和 N u N_u Nu 分别是积分的 OFDM 符号数量和每个 OFDM 符号中的总子载波数。同理，噪声基底的平均电平可以计算为

E { ∑ m ∈ T , p ∈ F ∣ χ [ m , p ] ∣ 2 } = E { ∣ χ n [ m , p ] ∣ 2 } = L N u E { ∣ N l , k ∣ 2 } . (37) \begin{aligned} E\left\{\sum_{m\in T,p\in F} |\chi[m, p]|^2\right\} &= E\{|\chi_n[m, p]|^2\} \\ &= L N_u E\left\{|N_{l,k}|^2\right\}. \end{aligned} \tag{37} E⎩ ⎨ ⎧m∈T,p∈F∑∣χ[m,p]∣2⎭ ⎬ ⎫=E{∣χn[m,p]∣2}=LNuE{∣Nl,k∣2}.(37)

将 (36) 和 (37) 代入 (34)，我们可以得到

S N R t a r ECA-C ≈ L N u ∣ a 0 ∣ 2 / E { ∣ N l , k ∣ 2 } , (38) SNR_{tar}^\text{ECA-C} \approx L N_u |a_0|^2 / E\left\{|N_{l,k}|^2\right\}, \tag{38} SNRtarECA-C≈LNu∣a0∣2/E{∣Nl,k∣2},(38)

其中 L N u L N_u LNu 是用于 CAF 计算的积分点数。

1. 初始定义

根据公式 (15)，噪声项的互模糊函数 (CAF) 定义为：
χ n [ m , p ] = ∑ l = 0 L − 1 e − j 2 π p l / L ∑ k = 0 N u − 1 N l , k C l , k ∗ e j 2 π N u k m \chi_n[m, p] = \sum_{l=0}^{L-1} e^{-j2\pi pl/L} \sum_{k=0}^{N_u-1} N_{l,k} C_{l,k}^* e^{j\frac{2\pi}{N_u}km} χn[m,p]=l=0∑L−1e−j2πpl/Lk=0∑Nu−1Nl,kCl,k∗ejNu2πkm
2. 展开模平方

我们要计算其期望功率 E { ∣ χ n [ m , p ] ∣ 2 } E\{ |\chi_n[m, p]|^2 \} E{∣χn[m,p]∣2}。首先将 ∣ χ n ∣ 2 |\chi_n|^2 ∣χn∣2 展开为 χ n ⋅ χ n ∗ \chi_n \cdot \chi_n^* χn⋅χn∗：
∣ χ n ∣ 2 = ( ∑ l = 0 L − 1 ∑ k = 0 N u − 1 e − j 2 π p l / L N l , k C l , k ∗ e j 2 π N u k m ) ⋅ ( ∑ l ′ = 0 L − 1 ∑ k ′ = 0 N u − 1 e j 2 π p l ′ / L N l ′ , k ′ ∗ C l ′ , k ′ e − j 2 π N u k ′ m ) \begin{aligned} |\chi_n|^2 &= \left( \sum_{l=0}^{L-1} \sum_{k=0}^{N_u-1} e^{-j2\pi pl/L} N_{l,k} C_{l,k}^* e^{j\frac{2\pi}{N_u}km} \right) \\ &\quad \cdot \left( \sum_{l'=0}^{L-1} \sum_{k'=0}^{N_u-1} e^{j2\pi pl'/L} N_{l',k'}^* C_{l',k'} e^{-j\frac{2\pi}{N_u}k'm} \right) \end{aligned} ∣χn∣2=(l=0∑L−1k=0∑Nu−1e−j2πpl/LNl,kCl,k∗ejNu2πkm)⋅(l′=0∑L−1k′=0∑Nu−1ej2πpl′/LNl′,k′∗Cl′,k′e−jNu2πk′m)

合并求和项并整理：
∣ χ n ∣ 2 = ∑ l , l ′ ∑ k , k ′ ( N l , k N l ′ , k ′ ∗ ) ( C l , k ∗ C l ′ , k ′ ) e − j 2 π L p ( l − l ′ ) e j 2 π N u m ( k − k ′ ) |\chi_n|^2 = \sum_{l, l'} \sum_{k, k'} \left( N_{l,k} N_{l',k'}^* \right) \left( C_{l,k}^* C_{l',k'} \right) e^{-j\frac{2\pi}{L}p(l-l')} e^{j\frac{2\pi}{N_u}m(k-k')} ∣χn∣2=l,l′∑k,k′∑(Nl,kNl′,k′∗)(Cl,k∗Cl′,k′)e−jL2πp(l−l′)ejNu2πm(k−k′)
3. 利用统计特性化简

对上式取期望 E { ⋅ } E\{\cdot\} E{⋅}，利用以下统计假设：

噪声独立性 ： N l , k N_{l,k} Nl,k 为高斯白噪声，不同样本间互不相关，即 E { N l , k N l ′ , k ′ ∗ } E\{ N_{l,k} N_{l',k'}^* \} E{Nl,kNl′,k′∗} 仅在 l = l ′ l=l' l=l′ 且 k = k ′ k=k' k=k′ 时不为 0。

信号与噪声独立 ： N N N 与 C C C 相互独立。

功率归一化 ： E { ∣ C l , k ∣ 2 } = 1 E\{|C_{l,k}|^2\} = 1 E{∣Cl,k∣2}=1。

利用假设 1（独立性），四重求和塌缩为双重求和（仅保留 l = l ′ , k = k ′ l=l', k=k' l=l′,k=k′ 的项），此时相位项指数为 0，值为 1：
E { ∣ χ n ∣ 2 } = ∑ l = 0 L − 1 ∑ k = 0 N u − 1 E { ∣ N l , k ∣ 2 } ⋅ E { ∣ C l , k ∣ 2 } ⋅ 1 = ∑ l = 0 L − 1 ∑ k = 0 N u − 1 E { ∣ N l , k ∣ 2 } ⋅ 1 \begin{aligned} E\{|\chi_n|^2\} &= \sum_{l=0}^{L-1} \sum_{k=0}^{N_u-1} E\{ |N_{l,k}|^2 \} \cdot E\{ |C_{l,k}|^2 \} \cdot 1 \\ &= \sum_{l=0}^{L-1} \sum_{k=0}^{N_u-1} E\{ |N_{l,k}|^2 \} \cdot 1 \end{aligned} E{∣χn∣2}=l=0∑L−1k=0∑Nu−1E{∣Nl,k∣2}⋅E{∣Cl,k∣2}⋅1=l=0∑L−1k=0∑Nu−1E{∣Nl,k∣2}⋅1
4. 最终结果

假设噪声功率 E { ∣ N l , k ∣ 2 } E\{ |N_{l,k}|^2 \} E{∣Nl,k∣2} 为常数，对 l l l (共 L L L 项) 和 k k k (共 N u N_u Nu 项) 进行累加：
E { ∑ m ∈ T , p ∈ F ∣ χ [ m , p ] ∣ 2 } = L N u E { ∣ N l , k ∣ 2 } (37) E\left\{\sum_{m\in T,p\in F} |\chi[m, p]|^2\right\} = L N_u E\left\{|N_{l,k}|^2\right\} \tag{37} E⎩ ⎨ ⎧m∈T,p∈F∑∣χ[m,p]∣2⎭ ⎬ ⎫=LNuE{∣Nl,k∣2}(37)
结论：由于噪声的非相干特性，其总功率是单个样本功率与总样本数 L N u LN_u LNu 的线性乘积（而非相干积累下的平方关系）。

RSD： 根据 IV-A 小节，RSD 方法执行的均衡操作将所有杂波能量集中在零多普勒处。杂波分量不影响目标峰值的平均电平，因为它们在 RD 图中通过多普勒频移与目标回波分开了。同样，将失配参考信号代入 χ t a r [ m , p ] \chi_{tar}[m, p] χtar[m,p]，可以得到目标峰值为

E { ∣ χ ~ [ n 0 , p 0 ] ∣ 2 } ≈ ∑ l = 0 L − 1 ∑ k = 0 N u − 1 ∣ a 0 ∣ 2 = L 2 N u 2 ∣ a 0 ∣ 2 , (39) E\{|\tilde{\chi}[n_0, p_0]|^2\} \approx \sum_{l=0}^{L-1} \sum_{k=0}^{N_u-1} |a_0|^2 = L^2 N_u^2 |a_0|^2, \tag{39} E{∣χ~[n0,p0]∣2}≈l=0∑L−1k=0∑Nu−1∣a0∣2=L2Nu2∣a0∣2,(39)

这似乎与 ECA-C 获得的结果完全相同。这意味着目标峰值的平均电平不受均衡操作的影响。另一方面，在 χ ~ n [ m , p ] \tilde{\chi}_n[m, p] χ~n[m,p] 中使用 (23)，我们可以得到噪声基底的平均电平

E { ∑ m ∈ T , p ∈ F ∣ χ ~ [ m , p ] ∣ 2 } = E { ∣ ∑ l = 0 L − 1 e − j 2 π p l / L ∑ k = 0 N u − 1 N l , k C l , k ∗ ∣ C l , k ∣ 2 e j 2 π N u k m ∣ 2 } = L N u E { ∣ N l , k ∣ 2 } E { 1 / ∣ C l , k ∣ 2 } = μ L N u E { ∣ N l , k ∣ 2 } , (40) \begin{aligned} &~~~~~E \left\{ \sum_{m \in T, p \in F} |\tilde{\chi}[m, p]|^2 \right\} \\ &= E \left\{ \left| \sum_{l=0}^{L-1} e^{-j2\pi pl/L} \sum_{k=0}^{N_u-1} N_{l,k} \frac{C_{l,k}^*}{|C_{l,k}|^2} e^{j\frac{2\pi}{N_u}km} \right|^2 \right\} \\ &= L N_u E \left\{ |N_{l,k}|^2 \right\} E \left\{ 1/|C_{l,k}|^2 \right\} \\ &= \mu L N_u E \left\{ |N_{l,k}|^2 \right\}, \end{aligned} \tag{40} E⎩ ⎨ ⎧m∈T,p∈F∑∣χ~[m,p]∣2⎭ ⎬ ⎫=E⎩ ⎨ ⎧ l=0∑L−1e−j2πpl/Lk=0∑Nu−1Nl,k∣Cl,k∣2Cl,k∗ejNu2πkm 2⎭ ⎬ ⎫=LNuE{∣Nl,k∣2}E{1/∣Cl,k∣2}=μLNuE{∣Nl,k∣2},(40)

其中

μ = E { 1 / ∣ C l , k ∣ 2 } . (41) \mu = E\left\{1/|C_{l,k}|^2\right\}. \tag{41} μ=E{1/∣Cl,k∣2}.(41)

最后，检测到的目标 SNR 可以写为

S N R t a r R S D = L N u ∣ a 0 ∣ 2 μ E { ∣ N l , k ∣ 2 } = 1 μ ⋅ S N R t a r E C A − C . (42) SNR_{tar}^{RSD} = \frac{L N_u |a_0|^2}{\mu E\left\{|N_{l,k}|^2\right\}} = \frac{1}{\mu} \cdot SNR_{tar}^{ECA-C}. \tag{42} SNRtarRSD=μE{∣Nl,k∣2}LNu∣a0∣2=μ1⋅SNRtarECA−C.(42)

参数 μ \mu μ 表明，RSD 方法获得的噪声基底平均电平取决于 OFDM 信号的调制方案。注意，

对于等模调制方案（例如 BPSK 和 QPSK），我们有 μ = 1 \mu = 1 μ=1。这表明三种子载波域算法表现出相同的噪声基底水平。
但在非等模调制方案的情况下，由于对于 16-QAM μ = 1.89 \mu = 1.89 μ=1.89，对于 64-QAM μ = 2.69 \mu = 2.69 μ=2.69， RSD 方法引起的噪声基底平均电平遗憾地高于其他两种子载波域算法。

这最终导致比 ECA-C 和 ACRF-C 方法更低的 SNR（例如，16-QAM 损失 2.76 dB 2.76\text{ dB} 2.76 dB，64-QAM 损失 4.29 dB 4.29\text{ dB} 4.29 dB）。

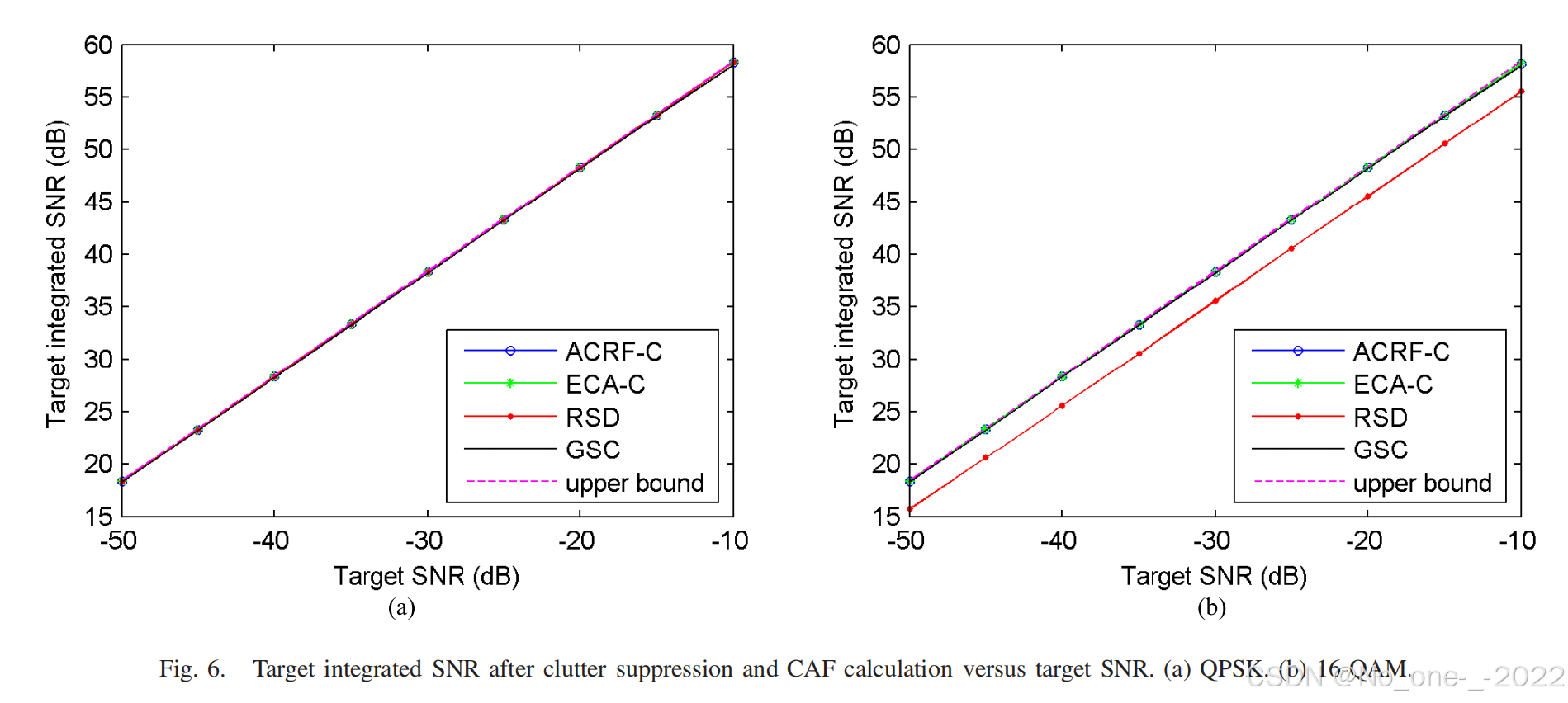
为了反映上述差异，我们将表 I 中的目标 SNR 从 − 50 dB -50\text{ dB} −50 dB 更改为 − 10 dB -10\text{ dB} −10 dB，步长为 5 dB 5\text{ dB} 5 dB。目标积分 SNR 的上限是通过将积分增益（即 68.4 dB 68.4\text{ dB} 68.4 dB）加到目标 SNR 获得的。在杂波抑制和 CAF 计算之后，从 RD 图中获得目标积分 SNR，这代表了杂波抑制性能。对每种算法在每个 SNR 下进行 100 次蒙特卡洛 (MC) 仿真，获得了如图 6 所示的仿真结果。如图 6(a) 所示，这些子载波域算法在等模调制方案中似乎具有相同的抑制性能，并且几乎与品红色虚线表示的上限重合。

相比之下，图 6(b) 表明，在 16-QAM 调制类型下，RSD 算法将目标 SNR 相比 ACRF-C 和 ECA-C 方法降低了约 2.83 dB 2.83\text{ dB} 2.83 dB，这与理论分析一致。同样，ACRF-C 和 ECA-C 方法在非等模调制方案中也能达到上限。需要注意的是，时域方法在图 6(a) 和图 6(b) 中几乎都获得了目标积分 SNR 的上限，因为它与发射波形无关。通常，就杂波抑制性能而言，

ACRF-C 和 ECA-C 方法在任何类型的调制方案下都能接近理论上限，并且三种子载波域算法在等模调制方案中完全相同。
然而，在非等模调制方案中，就目标 SNR 而言，RSD 算法的性能劣于 ACRF-C 和 ECA-C 方法。

C. Doppler Response

本质上，子载波域的方法是利用了每个子载波上杂波分量的时间相关性（即杂波随时间变化很小或不变的特性）来进行杂波抑制或旁瓣缓解的，并且依靠多普勒频率的差异来区分目标和杂波。
因此，子载波域杂波抑制算法的效果可以被看作是一种 零多普勒切除滤波器（zero-Doppler removal filters，即把多普勒频率为 0 的成分挖掉）。
可以想象，具有零多普勒频率或接近零多普勒频率的目标回波，也会因此被抑制或削弱。具体来说，我们可以注意到在公式 (17) 和 (32) 中，当目标的多普勒频率 f D , 0 f_{D,0} fD,0 小于多普勒分辨率 f 0 f_0 f0 时，原有的公式推导（即假设目标项趋于 0）就不再成立了。这意味着，在杂波抑制之后，这些（慢速）目标的回波预计也会被对消或削弱。在这种情况下，分析子载波域方法的多普勒响应，可以让我们深入了解它们对这类慢速移动目标的抑制性能（即会造成多大的信噪比损失）。

1. 信道估计中的目标分量

ACRF-C 算法通过对所有 OFDM 符号求平均来估计第 k k k 个子载波的信道响应 H ~ k \tilde{H}k H~k。根据公式 (16)，其完整表达式包含杂波、目标和噪声三项：
H ~ k = 1 L ∑ l = 0 L − 1 Y l , k C l , k = 1 L ∑ l = 0 L − 1 H l , k ⏟ 杂波项 + 1 L γ k ∑ l = 0 L − 1 e j 2 π f D , 0 l T e ⏟ 目标项 + 1 L ∑ l = 0 L − 1 N l , k C l , k ⏟ 噪声项 (16) \tilde{H}k = \frac{1}{L} \sum{l=0}^{L-1} \frac{Y{l,k}}{C_{l,k}} = \underbrace{\frac{1}{L} \sum_{l=0}^{L-1} H_{l,k}}{\text{杂波项}} + \underbrace{\frac{1}{L} \gamma_k \sum{l=0}^{L-1} e^{j2\pi f_{D,0} l T_e}}{\text{目标项}} + \underbrace{\frac{1}{L} \sum{l=0}^{L-1} \frac{N_{l,k}}{C_{l,k}}}_{\text{噪声项}} \tag{16} H~k=L1l=0∑L−1Cl,kYl,k=杂波项 L1l=0∑L−1Hl,k+目标项 L1γkl=0∑L−1ej2πfD,0lTe+噪声项 L1l=0∑L−1Cl,kNl,k(16)

其中，目标项 的具体形式由公式 (17) 给出：
TargetTerm k = γ k e j π f D , 0 ( L − 1 ) T e sin ⁡ ( π f D , 0 L T e ) L sin ⁡ ( π f D , 0 T e ) (17) \text{TargetTerm}k = \gamma_k e^{j\pi f{D,0}(L-1)T_e} \frac{\sin(\pi f_{D,0} L T_e)}{L \sin(\pi f_{D,0} T_e)} \tag{17} TargetTermk=γkejπfD,0(L−1)TeLsin(πfD,0Te)sin(πfD,0LTe)(17)
2. 狄利克雷核的关键特性

公式 (17) 中的核心部分是狄利克雷核。根据目标速度的不同，其表现如下：

快速目标 ( f D , 0 ≫ f 0 f_{D,0} \gg f_0 fD,0≫f0) ：
当 f D , 0 L T e ≫ 1 f_{D,0} L T_e \gg 1 fD,0LTe≫1 时，狄利克雷核趋近于 0。目标项在平均过程中被消除，信道估计 H ~ k \tilde{H}_k H~k 仅包含杂波（如公式 18 所示）。

慢速目标 ( f D , 0 < f 0 f_{D,0} < f_0 fD,0<f0) ：
当目标接近静止，即 f D , 0 → 0 f_{D,0} \to 0 fD,0→0 时，利用极限性质 lim ⁡ x → 0 sin ⁡ ( L x ) sin ⁡ ( x ) = L \lim_{x \to 0} \frac{\sin(Lx)}{\sin(x)} = L limx→0sin(x)sin(Lx)=L，公式 (17) 趋近于非零常数：
lim ⁡ f D , 0 → 0 sin ⁡ ( π f D , 0 L T e ) L sin ⁡ ( π f D , 0 T e ) ≈ 1 \lim_{f_{D,0} \to 0} \frac{\sin(\pi f_{D,0} L T_e)}{L \sin(\pi f_{D,0} T_e)} \approx 1 fD,0→0limLsin(πfD,0Te)sin(πfD,0LTe)≈1
这意味着目标能量 γ k \gamma_k γk 完整地泄露到了信道估计 H ~ k \tilde{H}_k H~k 中 ：
H ~ k ≈ 杂波 + γ k ( 此时估计值包含目标 ) \tilde{H}_k \approx \text{杂波} + \gamma_k \quad (\text{此时估计值包含目标}) H~k≈杂波+γk(此时估计值包含目标)

3. 抑制步骤中的"自我对消"

在子载波域执行杂波去除时，使用标准公式 (19)：
Y ~ l , k = Y l , k − H ~ k C l , k (19) \tilde{Y}{l,k} = Y{l,k} - \tilde{H}k C{l,k} \tag{19} Y~l,k=Yl,k−H~kCl,k(19)
Y ~ l , k = Y l , k − ( 杂波 + γ k ) C l , k = ( H l , k C l , k ⏟ 原始杂波 + γ k C l , k ⏟ 原始目标 ∗ + N l , k ) − ( 杂波 ⋅ C l , k ⏟ 估计杂波 + γ k C l , k ⏟ 估计出的目标 ) ≈ N l , k \begin{aligned} \tilde{Y}{l,k} &= Y{l,k} - \left( \text{杂波} + \gamma_k \right) C_{l,k} \\ &= (\underbrace{H_{l,k} C_{l,k}}{\text{原始杂波}} + \underbrace{\gamma_k C{l,k}}{\text{原始目标}^*} + N{l,k}) - (\underbrace{\text{杂波} \cdot C_{l,k}}{\text{估计杂波}} + \underbrace{\gamma_k C{l,k}}{\text{估计出的目标}}) \\ &\approx N{l,k} \end{aligned} Y~l,k=Yl,k−(杂波+γk)Cl,k=(原始杂波 Hl,kCl,k+原始目标∗ γkCl,k+Nl,k)−(估计杂波杂波⋅Cl,k+估计出的目标 γkCl,k)≈Nl,k

为简化推导，假设 f D , 0 ≈ 0 f_{D,0} \approx 0 fD,0≈0 时目标相位旋转项 e j 2 π f D , 0 l T e ≈ 1 e^{j2\pi f_{D,0}lT_e} \approx 1 ej2πfD,0lTe≈1，因此原始目标项近似为 γ k C l , k \gamma_k C_{l,k} γkCl,k

结论：由于 H ~ k \tilde{H}k H~k 错误地包含了慢速目标的特征 γ k \gamma_k γk，在执行减法操作时，目标回波 γ k C l , k \gamma_k C{l,k} γkCl,k 被自身的估计值抵消，导致目标信号丢失。

在本小节中，为了定量说明子载波域方法的多普勒响应，我们将表 I 中的目标多普勒频率以多普勒分辨率 f 0 f_0 f0 为步长，从 − 20 f 0 -20f_0 −20f0 更改为 20 f 0 20f_0 20f0 。与 IV-B 节相同，目标积分 SNR 是在进行 100 次蒙特卡洛 (MC) 仿真后，通过杂波抑制和 CAF 计算从 RD 图中获得的。为了进行比较，我们展示了时域方法 GSC，其载波频率偏移 (CFO) 杂波子空间约为 − 2 f 0 -2f_0 −2f0 到 2 f 0 2f_0 2f0 [32]。QPSK 和 16-QAM 的多普勒响应仿真结果如图 7 所示。从图 7 中，我们可以得出与 IV-A 节和 IV-B 节相同的结论。即，ACRF-C 和 ECA-C 可以在 QPSK 下产生很深的零多普勒零陷，但对于 16-QAM，只有 ECA-C 具有相当深的零陷。此外，在 16-QAM 调制类型下，RSD 方法使目标 SNR 降低了约 2.76 dB 2.76\text{ dB} 2.76 dB 。

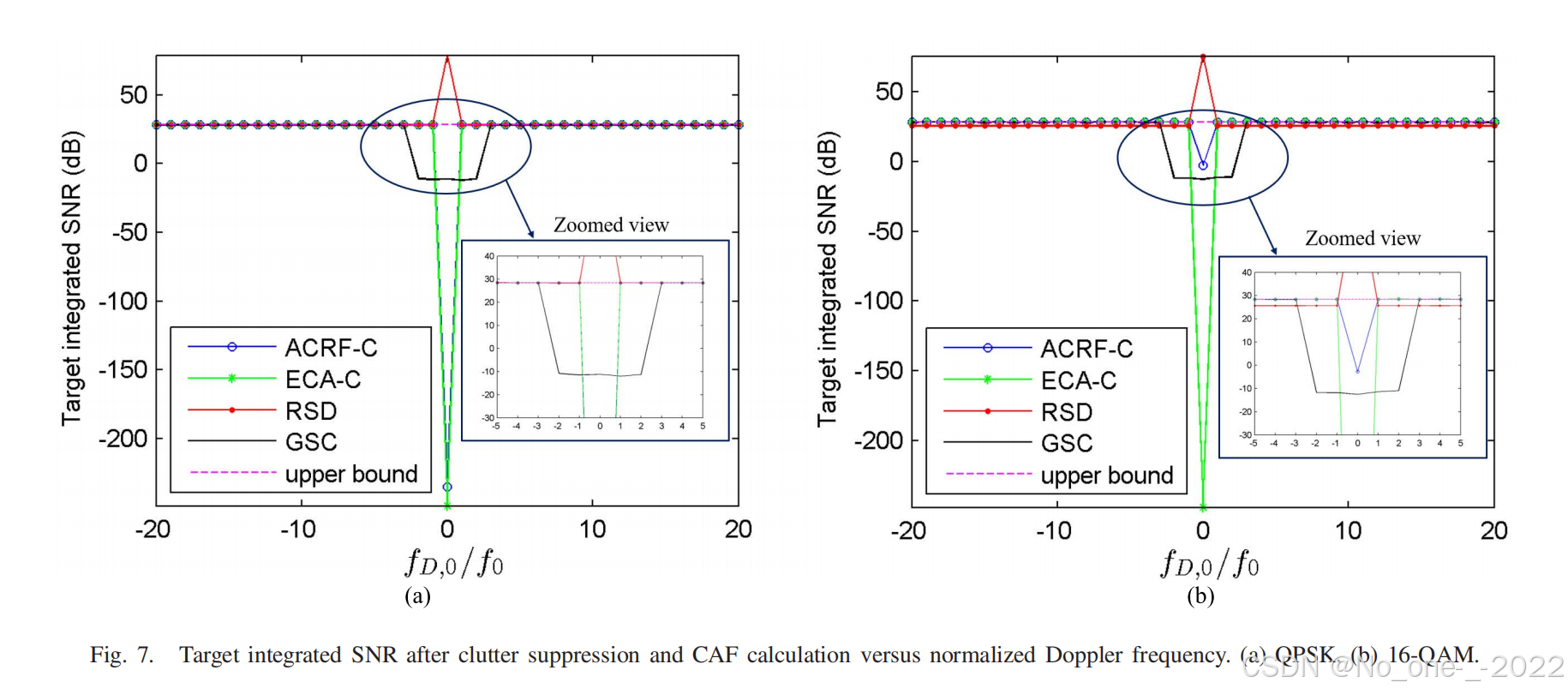
如图 7 所示，子载波域方法保持了足够窄的多普勒杂波零陷，从而不会屏蔽对慢速移动目标的检测。具体而言，当目标多普勒频率等于或大于多普勒分辨率时，目标积分 SNR 可以达到上限，这与 (17) 和 (32) 中的理论分析一致。

然而，由于 GSC 中构造了 CFO 杂波子空间，杂波抑制后 GSC 产生了一个明显的多普勒零陷。如图 7 中的放大图所示，当目标进入 CFO 杂波子空间时，目标积分 SNR 会被 GSC 削弱。因此，当目标靠近杂波时，GSC 可能会削弱积分增益。
但对于子载波域方法，只要目标多普勒频率不小于多普勒分辨率，预计就不会有积分增益损失。

此外，这些方法的多普勒响应也可以反映它们的时变杂波抑制性能。GSC 较宽的多普勒零陷使其在时变杂波抑制方面比子载波域方法更具鲁棒性。使用子载波域方法，只有小于多普勒分辨率的多普勒频率才会被抑制。对于杂波环境静止的情况，这是理想的。然而，如果关注时变杂波抑制，GSC 方法将是优先选择。