【笔记篇】【硬件基础篇】模拟电子技术基础 (童诗白) 第6章 信号的运算和处理

智嵌电子2025-12-27 14:42

模拟电子技术基础 童诗白

第6章 信号的运算和处理

本章核心问题概览

本章围绕集成运放和模拟乘法器构成的信号运算与处理电路展开，核心问题包括：

  • 基本运算电路（比例、加减、积分、微分、对数、指数）的构成与运算关系推导；
  • 模拟乘法器的工作原理及在乘方、除法、开方运算中的应用；
  • 有源滤波电路的分类、特性及分析方法（低通、高通、带通、带阻）；
  • 信号预处理专用放大电路（仪表、电荷、隔离放大器）的特点与应用；
  • 运算电路和滤波电路的误差来源及抑制措施。

6.1 基本运算电路

集成运放引入电压负反馈后工作在线性区，利用"虚短"（ u P = u N u_P = u_N uP=uN）和"虚断"（ i P = i N = 0 i_P = i_N = 0 iP=iN=0）特性，可实现多种模拟信号运算，是构成复杂信号处理电路的基础。

6.1.1 概述

1. 运算电路的核心特征
  • 必须引入电压负反馈，使集成运放工作在线性区；
  • 输出电压是输入电压的函数，实现特定数学运算（比例、积分、加减等）；
  • 分析基础：理想运放的"虚短"和"虚断"，辅助方法为节点电流法 和叠加原理。
2. 多级运算电路的分析原则
  • 前级输出电阻为零（电压负反馈特性），后级不影响前级运算关系；
  • 逐级分析每级运算关系，前级输出作为后级输入，最终推导总运算关系。

6.1.2 比例运算电路

比例运算电路是最基本的运算电路，分为反相、同相和电压跟随器三种形式。

1. 反相比例运算电路
（1）基本电路结构
  • 输入信号 u I u_I uI 经电阻 R R R 接入反相输入端，同相输入端经补偿电阻 R ′ R' R′ 接地；
  • 补偿电阻 R ′ = R ∥ R f R' = R \parallel R_f R′=R∥Rf，保证运放输入级差分电路外接电阻对称，减小失调电流影响。
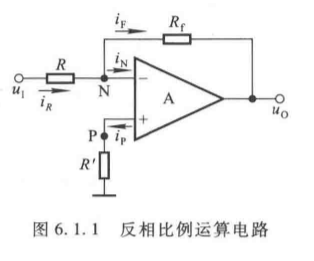
（2）运算关系推导

根据"虚短"（ u N = u P = 0 u_N = u_P = 0 uN=uP=0，虚地）和"虚断"（ i R = i F i_R = i_F iR=iF）：
u I − u N R = u N − u O R f \frac{u_I - u_N}{R} = \frac{u_N - u_O}{R_f} RuI−uN=RfuN−uO

代入 u N = 0 u_N = 0 uN=0，整理得：
u O = − R f R u I (6.1.3) u_O = -\frac{R_f}{R} u_I \tag{6.1.3} uO=−RRfuI(6.1.3)

  • 比例系数： A u f = − R f R A_{uf} = -\frac{R_f}{R} Auf=−RRf（负号表示反相）；
  • 输入电阻： R i = R R_i = R Ri=R（并联负反馈减小输入电阻）；
  • 输出电阻： R o = 0 R_o = 0 Ro=0（电压负反馈特性）。
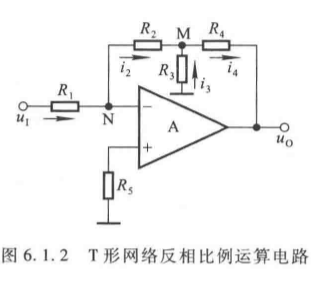
（3）T形网络反相比例运算电路

为解决"大比例系数与大输入电阻不可兼得"的问题，用T形网络替代 R f R_f Rf，电路如下：

  • 运算关系：
    u O = − R 2 + R 4 R 1 ( 1 + R 2 ∥ R 4 R 3 ) u I (6.1.5) u_O = -\frac{R_2 + R_4}{R_1} \left(1 + \frac{R_2 \parallel R_4}{R_3}\right) u_I \tag{6.1.5} uO=−R1R2+R4(1+R3R2∥R4)uI(6.1.5)
  • 优势：输入电阻 R i = R 1 R_i = R_1 Ri=R1（可较大），用小阻值电阻即可实现大比例系数。
2. 同相比例运算电路
（1）基本电路结构
  • 输入信号 u I u_I uI 接入同相输入端，反相输入端经电阻 R R R 接地，反馈电阻 R f R_f Rf 跨接反相输入端与输出端。
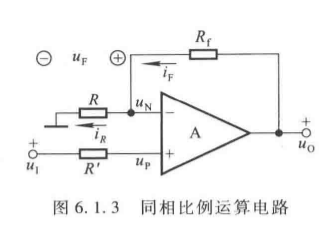
（2）运算关系推导

根据"虚短"（ u N = u P = u I u_N = u_P = u_I uN=uP=uI）和"虚断"（ i R = i F i_R = i_F iR=iF）：
u N − 0 R = u O − u N R f \frac{u_N - 0}{R} = \frac{u_O - u_N}{R_f} RuN−0=RfuO−uN

整理得：
u O = ( 1 + R f R ) u I (6.1.8) u_O = \left(1 + \frac{R_f}{R}\right) u_I \tag{6.1.8} uO=(1+RRf)uI(6.1.8)

  • 比例系数： A u f = 1 + R f R A_{uf} = 1 + \frac{R_f}{R} Auf=1+RRf（正号表示同相，且 A u f ≥ 1 A_{uf} \geq 1 Auf≥1）；
  • 输入电阻： R i → ∞ R_i \to \infty Ri→∞（串联负反馈增大输入电阻）；
  • 特点：存在共模输入电压（ u I C = u I u_{IC} = u_I uIC=uI），需选用高共模抑制比（ K C M R K_{CMR} KCMR）的运放。
3. 电压跟随器
（1）电路结构

将同相比例电路的 R f R_f Rf 短路、 R R R 开路，即构成电压跟随器：

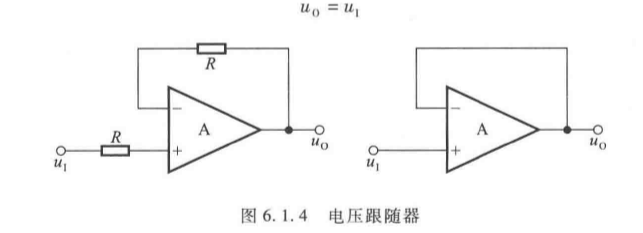
（2）运算关系

u O = u I (6.1.9) u_O = u_I \tag{6.1.9} uO=uI(6.1.9)

  • 特性： A u f = 1 A_{uf} = 1 Auf=1、 R i → ∞ R_i \to \infty Ri→∞、 R o = 0 R_o = 0 Ro=0，跟随特性优于射极输出器，用于隔离、缓冲或阻抗变换。

6.1.3 加减运算电路

实现多个输入信号的求和或求差运算，分为反相加法、同相加法和加减运算三种形式。

1. 反相加法运算电路
（1）电路结构

多个输入信号均接入反相输入端：

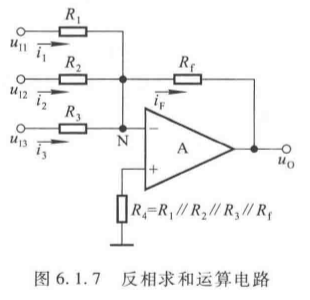
（2）运算关系推导

根据"虚地"（ u N = 0 u_N = 0 uN=0）和"虚断"（ i 1 + i 2 + i 3 = i F i_1 + i_2 + i_3 = i_F i1+i2+i3=iF）：
u I 1 R 1 + u I 2 R 2 + u I 3 R 3 = − u O R f \frac{u_{I1}}{R_1} + \frac{u_{I2}}{R_2} + \frac{u_{I3}}{R_3} = -\frac{u_O}{R_f} R1uI1+R2uI2+R3uI3=−RfuO

整理得：
u O = − R f ( u I 1 R 1 + u I 2 R 2 + u I 3 R 3 ) (6.1.10) u_O = -R_f \left( \frac{u_{I1}}{R_1} + \frac{u_{I2}}{R_2} + \frac{u_{I3}}{R_3} \right) \tag{6.1.10} uO=−Rf(R1uI1+R2uI2+R3uI3)(6.1.10)

  • 补偿电阻： R ′ = R 1 ∥ R 2 ∥ R 3 ∥ R f R' = R_1 \parallel R_2 \parallel R_3 \parallel R_f R′=R1∥R2∥R3∥Rf；
  • 特点：各输入信号相互独立，输入电阻低（取决于各输入电阻 R 1 , R 2 , R 3 R_1, R_2, R_3 R1,R2,R3）。
2. 同相加法运算电路
（1）电路结构

多个输入信号均接入同相输入端：

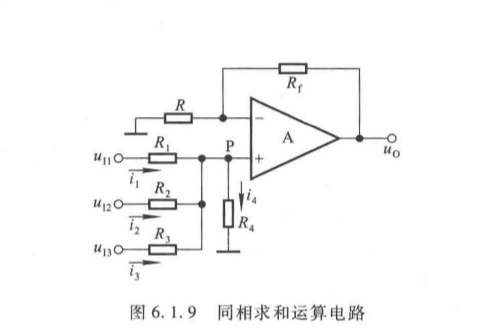
（2）运算关系推导

先求同相输入端电位 u P u_P uP（节点电流法）：
u I 1 − u P R 1 + u I 2 − u P R 2 + u I 3 − u P R 3 = u P R 4 \frac{u_{I1} - u_P}{R_1} + \frac{u_{I2} - u_P}{R_2} + \frac{u_{I3} - u_P}{R_3} = \frac{u_P}{R_4} R1uI1−uP+R2uI2−uP+R3uI3−uP=R4uP

整理得：
u P = R P ( u I 1 R 1 + u I 2 R 2 + u I 3 R 3 ) (6.1.11) u_P = R_P \left( \frac{u_{I1}}{R_1} + \frac{u_{I2}}{R_2} + \frac{u_{I3}}{R_3} \right) \tag{6.1.11} uP=RP(R1uI1+R2uI2+R3uI3)(6.1.11)

其中 R P = R 1 ∥ R 2 ∥ R 3 ∥ R 4 R_P = R_1 \parallel R_2 \parallel R_3 \parallel R_4 RP=R1∥R2∥R3∥R4。

再根据同相比例运算关系 u O = ( 1 + R f R ) u P u_O = \left(1 + \frac{R_f}{R}\right) u_P uO=(1+RRf)uP，代入 u P u_P uP 得：
u O = ( 1 + R f R ) R P ( u I 1 R 1 + u I 2 R 2 + u I 3 R 3 ) u_O = \left(1 + \frac{R_f}{R}\right) R_P \left( \frac{u_{I1}}{R_1} + \frac{u_{I2}}{R_2} + \frac{u_{I3}}{R_3} \right) uO=(1+RRf)RP(R1uI1+R2uI2+R3uI3)

若满足 R ∥ R f = R P R \parallel R_f = R_P R∥Rf=RP（平衡条件），则：
u O = R f ( u I 1 R 1 + u I 2 R 2 + u I 3 R 3 ) (6.1.13) u_O = R_f \left( \frac{u_{I1}}{R_1} + \frac{u_{I2}}{R_2} + \frac{u_{I3}}{R_3} \right) \tag{6.1.13} uO=Rf(R1uI1+R2uI2+R3uI3)(6.1.13)

  • 特点：输入电阻高，但各输入信号相互影响，计算复杂。
3. 加减运算电路
（1）电路结构

输入信号分别接入反相和同相输入端：

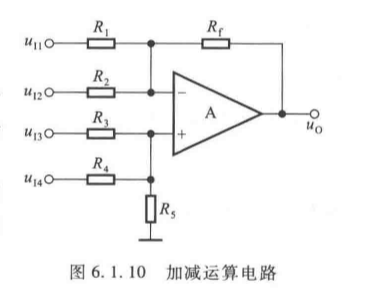
（2）运算关系推导（叠加原理）
  • 反相端输入 u I 1 , u I 2 u_{I1}, u_{I2} uI1,uI2 单独作用： u O 1 = − R f ( u I 1 R 1 + u I 2 R 2 ) u_{O1} = -R_f \left( \frac{u_{I1}}{R_1} + \frac{u_{I2}}{R_2} \right) uO1=−Rf(R1uI1+R2uI2)；
  • 同相端输入 u I 3 , u I 4 u_{I3}, u_{I4} uI3,uI4 单独作用： u O 2 = R f ( u I 3 R 3 + u I 4 R 4 ) u_{O2} = R_f \left( \frac{u_{I3}}{R_3} + \frac{u_{I4}}{R_4} \right) uO2=Rf(R3uI3+R4uI4)（满足平衡条件 R 1 ∥ R 2 ∥ R f = R 3 ∥ R 4 ∥ R 5 R_1 \parallel R_2 \parallel R_f = R_3 \parallel R_4 \parallel R_5 R1∥R2∥Rf=R3∥R4∥R5）；
  • 总输出：
    u O = R f ( u I 3 R 3 + u I 4 R 4 − u I 1 R 1 − u I 2 R 2 ) (6.1.15) u_O = R_f \left( \frac{u_{I3}}{R_3} + \frac{u_{I4}}{R_4} - \frac{u_{I1}}{R_1} - \frac{u_{I2}}{R_2} \right) \tag{6.1.15} uO=Rf(R3uI3+R4uI4−R1uI1−R2uI2)(6.1.15)
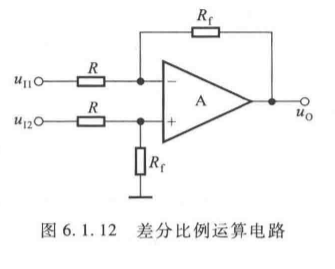
（3）差分比例运算电路（特殊情况）

当输入信号为两个（ u I 1 u_{I1} uI1 反相， u I 2 u_{I2} uI2 同相）且参数对称（ R 1 = R 2 = R R_1 = R_2 = R R1=R2=R， R 3 = R 4 = R f R_3 = R_4 = R_f R3=R4=Rf）：
u O = R f R ( u I 2 − u I 1 ) (6.1.16) u_O = \frac{R_f}{R} (u_{I2} - u_{I1}) \tag{6.1.16} uO=RRf(uI2−uI1)(6.1.16)

  • 特点：抑制共模信号，放大差模信号，输入电阻适中。

6.1.4 积分运算电路和微分运算电路

积分和微分是互逆运算，利用电容的充放电特性实现，广泛应用于波形变换和控制系统。

1. 积分运算电路
（1）基本电路结构
  • 反相输入端经电阻 R R R 接输入信号，反馈支路为电容 C C C；
  • 补偿电阻 R ′ = R R' = R R′=R（平衡输入电阻）。
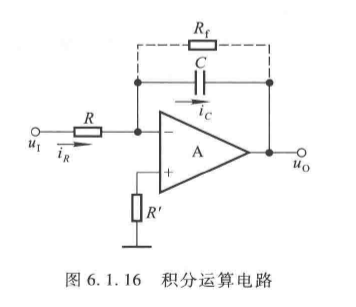
（2）运算关系推导

根据"虚地"（ u N = 0 u_N = 0 uN=0）和"虚断"（ i R = i C i_R = i_C iR=iC）：
i C = i R = u I R i_C = i_R = \frac{u_I}{R} iC=iR=RuI

电容电压 u C = 1 C ∫ i C d t u_C = \frac{1}{C} \int i_C dt uC=C1∫iCdt，而 u O = − u C u_O = -u_C uO=−uC，故：
u O = − 1 R C ∫ u I d t (6.1.18) u_O = -\frac{1}{RC} \int u_I dt \tag{6.1.18} uO=−RC1∫uIdt(6.1.18)

  • 定积分形式（ t 1 t_1 t1 到 t 2 t_2 t2 时间段）：
    u O = − 1 R C ∫ t 1 t 2 u I d t + u O ( t 1 ) (6.1.19) u_O = -\frac{1}{RC} \int_{t_1}^{t_2} u_I dt + u_O(t_1) \tag{6.1.19} uO=−RC1∫t1t2uIdt+uO(t1)(6.1.19)
    其中 u O ( t 1 ) u_O(t_1) uO(t1) 为积分起始时刻的输出电压。
（3）实用积分电路

为防止低频信号增益过大导致运放饱和，在电容 C C C 上并联电阻 R f R_f Rf（限制直流增益）：

  • 特点：可实现方波→三角波、正弦波→余弦波的波形变换。
2. 微分运算电路
（1）基本电路结构

将积分电路的 R R R 和 C C C 互换：

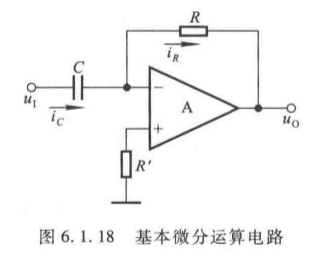
（2）运算关系推导

根据"虚地"（ u N = 0 u_N = 0 uN=0）和"虚断"（ i C = i R i_C = i_R iC=iR）：
i C = C d u I d t , i R = − u O R i_C = C \frac{du_I}{dt}, \quad i_R = -\frac{u_O}{R} iC=CdtduI,iR=−RuO

整理得：
u O = − R C d u I d t (6.1.21) u_O = -RC \frac{du_I}{dt} \tag{6.1.21} uO=−RCdtduI(6.1.21)

  • 特点：输出与输入电压的变化率成正比，对高频噪声敏感，稳定性差。
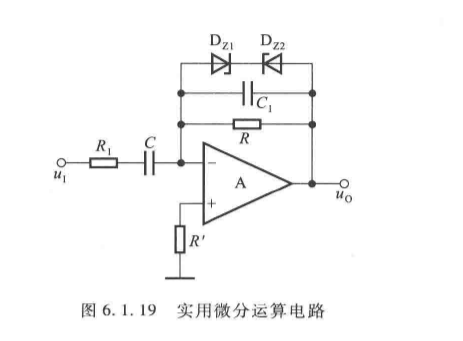
（3）实用微分电路

为改善稳定性和抑制噪声，引入限流电阻 R 1 R_1 R1 和相位补偿电容 C 1 C_1 C1：

  • 功能：方波→尖顶波变换，用于脉冲信号检测。
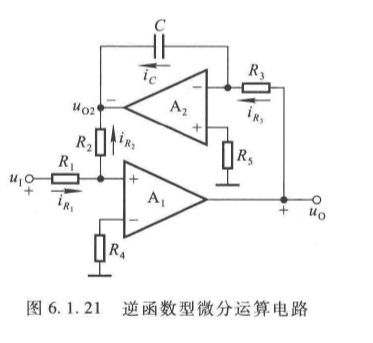
（4）逆函数型微分电路

利用积分电路作为负反馈通路，避免基本微分电路的稳定性问题：
u O = R 2 R 3 C R 1 ⋅ d u I d t (6.1.22) u_O = \frac{R_2 R_3 C}{R_1} \cdot \frac{du_I}{dt} \tag{6.1.22} uO=R1R2R3C⋅dtduI(6.1.22)

  • 优势：稳定性好，抗干扰能力强。

6.1.5 对数运算电路和指数运算电路

利用PN结的指数伏安特性，实现对数和指数运算，是构成乘法、除法运算的基础。

1. 对数运算电路
（1）晶体管对数电路
  • 晶体管接在反馈支路，利用发射结正向电流与电压的指数关系： i C ≈ I S e u B E U T i_C \approx I_S e^{\frac{u_{BE}}{U_T}} iC≈ISeUTuBE。
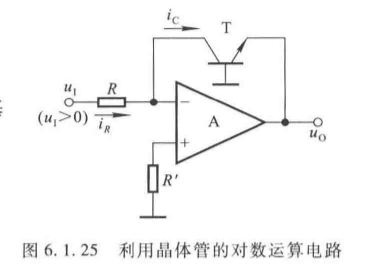
（2）运算关系推导

根据"虚地"（ u N = 0 u_N = 0 uN=0）和"虚断"（ i R = i C i_R = i_C iR=iC）：
i C = u I R , u B E = U T ln ⁡ i C I S i_C = \frac{u_I}{R}, \quad u_{BE} = U_T \ln \frac{i_C}{I_S} iC=RuI,uBE=UTlnISiC

输出电压 u O = − u B E u_O = -u_{BE} uO=−uBE，故：
u O = − U T ln ⁡ u I I S R (6.1.24) u_O = -U_T \ln \frac{u_I}{I_S R} \tag{6.1.24} uO=−UTlnISRuI(6.1.24)

  • 注意： u I > 0 u_I > 0 uI>0（保证晶体管导通），运算精度受温度影响（ I S I_S IS、 U T U_T UT 随温度变化）。
（3）集成对数电路

采用双晶体管补偿温度误差，核心关系：
u O ≈ − ( 1 + R 2 R 5 ) U T ln ⁡ u I I R R 3 u_O \approx -\left(1 + \frac{R_2}{R_5}\right) U_T \ln \frac{u_I}{I_R R_3} uO≈−(1+R5R2)UTlnIRR3uI

  • 热敏电阻 R 5 R_5 R5 补偿 U T U_T UT 的温度漂移。
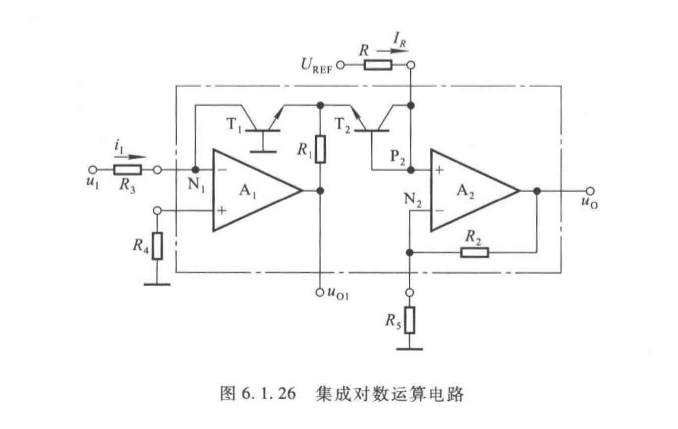
2. 指数运算电路
（1）电路结构

将对数电路的晶体管与电阻互换：

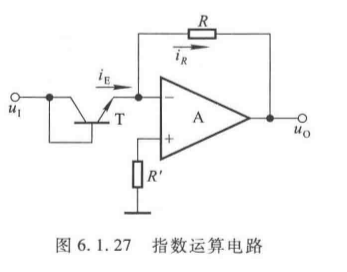
（2）运算关系推导

根据"虚地"（ u N = 0 u_N = 0 uN=0）和 u B E = u I u_{BE} = u_I uBE=uI：
i C ≈ I S e u I U T , u O = − i C R i_C \approx I_S e^{\frac{u_I}{U_T}}, \quad u_O = -i_C R iC≈ISeUTuI,uO=−iCR

整理得：
u O = − I S R e u I U T (6.1.25) u_O = -I_S R e^{\frac{u_I}{U_T}} \tag{6.1.25} uO=−ISReUTuI(6.1.25)

  • 注意： u I > 0 u_I > 0 uI>0 且范围小（发射结导通电压附近），需温度补偿。

6.1.6 乘法和除法运算电路（基于对数/指数）

利用"对数求和→指数"的组合，实现乘法运算；"对数求差→指数"实现除法运算。

1. 乘法运算电路
（1）原理框图

u I 1 → 对数 → u O 1 = − U T ln ⁡ u I 1 I S R u I 2 → 对数 → u O 2 = − U T ln ⁡ u I 2 I S R u O 3 = − ( u O 1 + u O 2 ) → 指数 → u O = − u I 1 u I 2 I S R u_{I1} \to \text{对数} \to u_{O1} = -U_T \ln \frac{u_{I1}}{I_S R} \\ u_{I2} \to \text{对数} \to u_{O2} = -U_T \ln \frac{u_{I2}}{I_S R} \\ u_{O3} = -(u_{O1} + u_{O2}) \to \text{指数} \to u_O = -\frac{u_{I1} u_{I2}}{I_S R} uI1→对数→uO1=−UTlnISRuI1uI2→对数→uO2=−UTlnISRuI2uO3=−(uO1+uO2)→指数→uO=−ISRuI1uI2

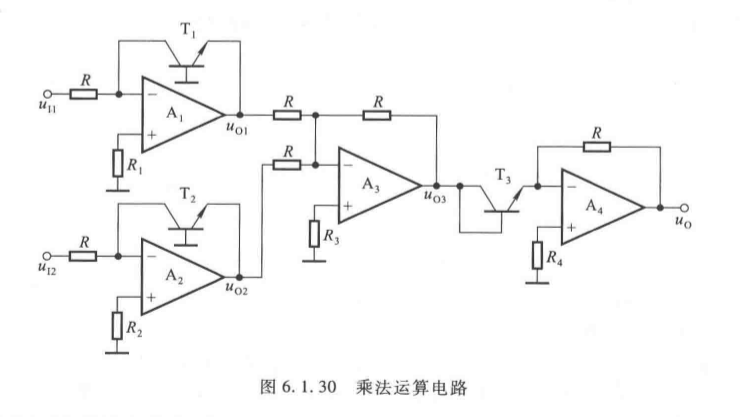
（2）核心公式

u O ≈ − u I 1 u I 2 I S R (6.1.26) u_O \approx -\frac{u_{I1} u_{I2}}{I_S R} \tag{6.1.26} uO≈−ISRuI1uI2(6.1.26)

  • 特点：实现两信号相乘，需保证 u I 1 , u I 2 > 0 u_{I1}, u_{I2} > 0 uI1,uI2>0（单象限乘法）。
2. 除法运算电路

将求和电路改为求差电路，核心公式：
u O ≈ − u I 1 R I S u I 2 u_O \approx -\frac{u_{I1} R}{I_S u_{I2}} uO≈−ISuI2uI1R

  • 注意： u I 2 u_{I2} uI2 极性固定（保证分母不为零且晶体管导通）。

6.1.7 运放非理想特性对运算误差的影响

实际运放的非理想参数（ A o d A_{od} Aod、 r i d r_{id} rid、 K C M R K_{CMR} KCMR、失调电压 U I O U_{IO} UIO 等）会引入运算误差，核心影响如下：

  1. A o d A_{od} Aod 和 r i d r_{id} rid 有限 ：反相比例电路的相对误差 δ ≈ − R f R f + A o d R N \delta \approx -\frac{R_f}{R_f + A_{od} R_N} δ≈−Rf+AodRNRf（ R N R_N RN 为等效并联电阻）， A o d A_{od} Aod、 r i d r_{id} rid 越大，误差越小；
  2. K C M R K_{CMR} KCMR 有限 ：同相比例电路的相对误差 δ ≈ 1 K C M R \delta \approx \frac{1}{K_{CMR}} δ≈KCMR1， K C M R K_{CMR} KCMR 越大，误差越小；
  3. 失调参数（ U I O U_{IO} UIO、 I I O I_{IO} IIO） ：积分电路的误差 Δ u O = − 1 C ∫ ( U I O R + I I O ) d t \Delta u_O = -\frac{1}{C} \int \left( \frac{U_{IO}}{R} + I_{IO} \right) dt ΔuO=−C1∫(RUIO+IIO)dt，需选用低失调运放或加调零电路。

6.2 模拟乘法器及其在运算电路中的应用

模拟乘法器是实现两模拟信号相乘的非线性器件，核心功能为 u O = k u X u Y u_O = k u_X u_Y uO=kuXuY（ k k k 为乘积系数），广泛应用于乘方、除法、开方等运算。

6.2.1 模拟乘法器简介

1. 核心参数
  • 输入电阻 r i 1 , r i 2 r_{i1}, r_{i2} ri1,ri2：理想情况下为 ∞ \infty ∞；
  • 输出电阻 r o r_o ro：理想情况下为 0 0 0；
  • 乘积系数 k k k：典型值为 ± 0.1 ∼ ± 1   V − 1 \pm 0.1 \sim \pm 1 \, \text{V}^{-1} ±0.1∼±1V−1；
  • 象限特性：单象限（ u X , u Y u_X, u_Y uX,uY 均为正）、两象限（一正一负）、四象限（均可正可负）。
2. 变跨导型乘法器工作原理

利用差分放大电路的跨导随输入电压变化的特性，核心关系：
g m = I 0 2 U T , u O = − g m R c u X = − I 0 R c 2 U T u X g_m = \frac{I_0}{2 U_T}, \quad u_O = -g_m R_c u_X = -\frac{I_0 R_c}{2 U_T} u_X gm=2UTI0,uO=−gmRcuX=−2UTI0RcuX

若 I 0 I_0 I0 由 u Y u_Y uY 控制（ I 0 ∝ u Y I_0 \propto u_Y I0∝uY），则 u O ∝ u X u Y u_O \propto u_X u_Y uO∝uXuY，实现乘法运算。

6.2.2 模拟乘法器的典型应用

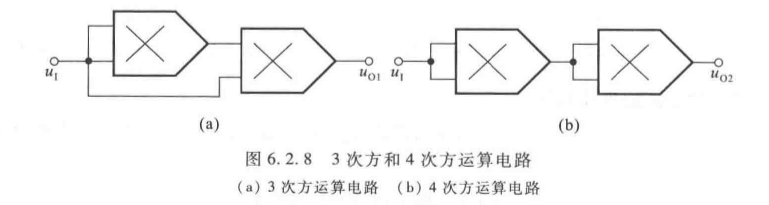
1. 乘方运算电路

将两个输入信号短接（ u X = u Y = u I u_X = u_Y = u_I uX=uY=uI），核心公式：
u O = k u I 2 (6.2.12) u_O = k u_I^2 \tag{6.2.12} uO=kuI2(6.2.12)

  • 扩展：多级串联实现高次幂运算（如 u O = k 2 u I 3 u_O = k^2 u_I^3 uO=k2uI3、 u O = k 2 u I 4 u_O = k^2 u_I^4 uO=k2uI4），但级数不宜过多（误差累积）。
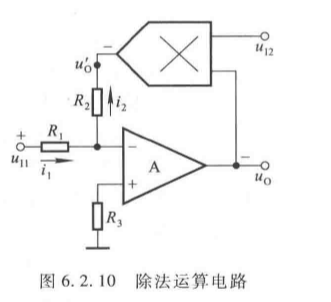
2. 除法运算电路

将模拟乘法器置于运放负反馈通路，构成逆函数型电路：

  • 运算关系推导（虚地、虚断）：
    u I 1 R 1 = − k u I 2 u O R 2    ⟹    u O = − R 2 k R 1 ⋅ u I 1 u I 2 (6.2.15) \frac{u_{I1}}{R_1} = -\frac{k u_{I2} u_O}{R_2} \implies u_O = -\frac{R_2}{k R_1} \cdot \frac{u_{I1}}{u_{I2}} \tag{6.2.15} R1uI1=−R2kuI2uO⟹uO=−kR1R2⋅uI2uI1(6.2.15)
  • 注意：需保证负反馈（ k u I 2 > 0 k u_{I2} > 0 kuI2>0 或 k u I 2 < 0 k u_{I2} < 0 kuI2<0），避免自激。
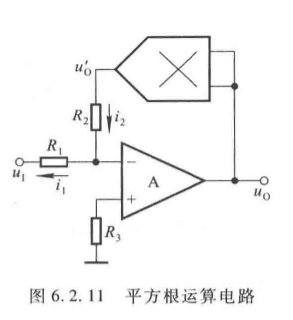
3. 开方运算电路

令除法电路的 u I 2 = u O u_{I2} = u_O uI2=uO，构成平方根电路：

  • 运算关系推导：
    − u I R 1 = k u O 2 R 2    ⟹    ∣ u O ∣ = − R 2 u I k R 1 (6.2.17) \frac{-u_I}{R_1} = \frac{k u_O^2}{R_2} \implies |u_O| = \sqrt{-\frac{R_2 u_I}{k R_1}} \tag{6.2.17} R1−uI=R2kuO2⟹∣uO∣=−kR1R2uI (6.2.17)
  • 注意：根号内为正（ u I u_I uI 与 k k k 反号），串联二极管防止运放闭锁（正反馈导致饱和）。
4. 二倍频电路

输入正弦波 u I = 2 U i sin ⁡ ω t u_I = \sqrt{2} U_i \sin \omega t uI=2 Uisinωt，输出：
u O = k u I 2 = k U i 2 ( 1 − cos ⁡ 2 ω t ) u_O = k u_I^2 = k U_i^2 (1 - \cos 2\omega t) uO=kuI2=kUi2(1−cos2ωt)

  • 滤除直流分量后，得到二倍频交流信号。

6.3 有源滤波电路

滤波电路是对特定频率信号进行选通的电路，有源滤波电路由 R C RC RC 网络和集成运放组成，具有放大和滤波双重功能，适用于小信号处理。

6.3.1 滤波电路基础知识

1. 分类与幅频特性
类型 功能 理想幅频特性
低通（LPF） 允许低频信号通过，衰减高频信号 通带 f < f p f < f_p f<fp，阻带 f > f p f > f_p f>fp
高通（HPF） 允许高频信号通过，衰减低频信号 通带 f > f p f > f_p f>fp，阻带 f < f p f < f_p f<fp
带通（BPF） 允许某一频段信号通过，衰减其他频率 通带 f p 1 < f < f p 2 f_{p1} < f < f_{p2} fp1<f<fp2，阻带 f < f p 1 f < f_{p1} f<fp1 或 f > f p 2 f > f_{p2} f>fp2
带阻（BEF） 衰减某一频段信号，允许其他频率通过 阻带 f p 1 < f < f p 2 f_{p1} < f < f_{p2} fp1<f<fp2，通带 f < f p 1 f < f_{p1} f<fp1 或 f > f p 2 f > f_{p2} f>fp2
全通（APF） 所有频率信号均通过，仅改变相位 幅值不变，相位随频率变化
  • 关键参数：通带放大倍数 A u p A_{up} Aup、通带截止频率 f p f_p fp（幅值衰减到 0.707 A u p 0.707 A_{up} 0.707Aup 对应的频率）、品质因数 Q = f 0 f b w Q = \frac{f_0}{f_{bw}} Q=fbwf0（ f 0 f_0 f0 为中心频率， f b w f_{bw} fbw 为通带宽度）、过渡带斜率（阶数越高，斜率越大，选择性越好）。
2. 无源与有源滤波的区别
  • 无源滤波（ R , C , L R, C, L R,C,L 组成）：无放大功能，带负载后滤波特性变差；
  • 有源滤波（ R , C + R, C + R,C+ 运放）：有放大功能，输入电阻高、输出电阻低，带负载后特性稳定。
3. 传递函数

用拉普拉斯变换分析，传递函数 A u ( s ) = U O ( s ) U I ( s ) A_u(s) = \frac{U_O(s)}{U_I(s)} Au(s)=UI(s)UO(s)， s = j ω s = j\omega s=jω 时可得到频率特性。分母中 s s s 的最高阶数即为滤波器的阶数（一阶、二阶等）。

6.3.2 低通滤波器（LPF）

以低通滤波器为例，阐明有源滤波电路的分析方法。

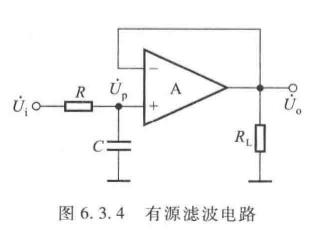
1. 一阶低通滤波器
（1）电路结构（同相输入）
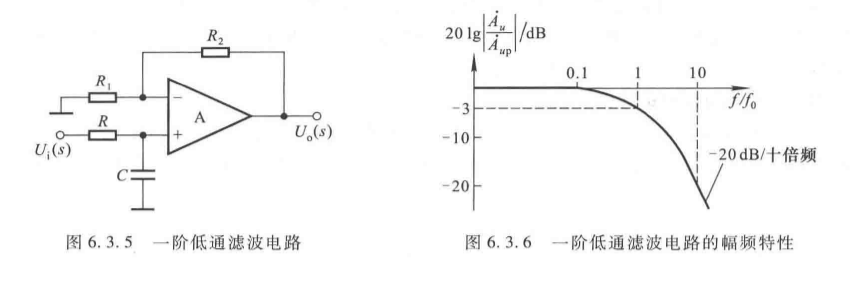
（2）传递函数与频率特性

传递函数：
A u ( s ) = ( 1 + R f R 1 ) ⋅ 1 1 + s R C (6.3.6) A_u(s) = \left(1 + \frac{R_f}{R_1}\right) \cdot \frac{1}{1 + s RC} \tag{6.3.6} Au(s)=(1+R1Rf)⋅1+sRC1(6.3.6)

令 f 0 = 1 2 π R C f_0 = \frac{1}{2\pi RC} f0=2πRC1（特征频率），频率特性：
A ˙ u = A u p 1 + j f f 0 \dot{A}u = \frac{A{up}}{1 + j \frac{f}{f_0}} A˙u=1+jf0fAup

  • 通带放大倍数 A u p = 1 + R f R 1 A_{up} = 1 + \frac{R_f}{R_1} Aup=1+R1Rf；
  • 通带截止频率 f p = f 0 f_p = f_0 fp=f0；
  • 过渡带斜率： − 20   dB/十倍频 -20 \, \text{dB/十倍频} −20dB/十倍频（选择性差）。
2. 二阶低通滤波器

增加 R C RC RC 环节，过渡带斜率提升至 − 40   dB/十倍频 -40 \, \text{dB/十倍频} −40dB/十倍频，常用压控电压源型。

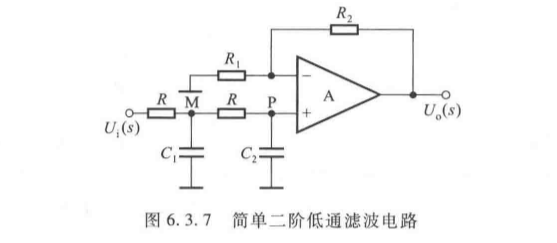
（1）压控电压源二阶低通滤波器
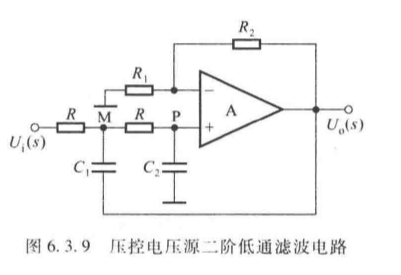
（2）传递函数与频率特性

传递函数：
A u ( s ) = A u p 1 + ( 3 − A u p ) s R C + ( s R C ) 2 (6.3.14) A_u(s) = \frac{A_{up}}{1 + (3 - A_{up}) s RC + (s RC)^2} \tag{6.3.14} Au(s)=1+(3−Aup)sRC+(sRC)2Aup(6.3.14)

频率特性（ f 0 = 1 2 π R C f_0 = \frac{1}{2\pi RC} f0=2πRC1）：
A ˙ u = A u p 1 − ( f f 0 ) 2 + j ( 3 − A u p ) f f 0 \dot{A}u = \frac{A{up}}{1 - \left(\frac{f}{f_0}\right)^2 + j (3 - A_{up}) \frac{f}{f_0}} A˙u=1−(f0f)2+j(3−Aup)f0fAup

  • 品质因数 Q = 1 ∣ 3 − A u p ∣ Q = \frac{1}{|3 - A_{up}|} Q=∣3−Aup∣1： Q Q Q 越大， f 0 f_0 f0 附近幅值越大，选择性越好（ Q = 0.707 Q = 0.707 Q=0.707 时为巴特沃斯滤波，幅频特性最平坦）；
  • 稳定性： A u p < 3 A_{up} < 3 Aup<3（避免自激）。
3. 高阶低通滤波器

由多个二阶低通滤波器串联组成，过渡带斜率为 − 20 n   dB/十倍频 -20n \, \text{dB/十倍频} −20ndB/十倍频（ n n n 为阶数），选择性更优。

6.3.3 其他类型有源滤波电路

1. 高通滤波器（HPF）

与低通滤波器呈对偶关系，将 R C RC RC 网络的电阻和电容互换即可。

（1）压控电压源二阶高通滤波器

传递函数：
A u ( s ) = A u p ⋅ ( s R C ) 2 1 + ( 3 − A u p ) s R C + ( s R C ) 2 (6.3.25) A_u(s) = A_{up} \cdot \frac{(s RC)^2}{1 + (3 - A_{up}) s RC + (s RC)^2} \tag{6.3.25} Au(s)=Aup⋅1+(3−Aup)sRC+(sRC)2(sRC)2(6.3.25)

  • 通带放大倍数 A u p = 1 + R f R 1 A_{up} = 1 + \frac{R_f}{R_1} Aup=1+R1Rf；
  • 通带截止频率 f p = 1 2 π R C f_p = \frac{1}{2\pi RC} fp=2πRC1；
  • 过渡带斜率： + 40   dB/十倍频 +40 \, \text{dB/十倍频} +40dB/十倍频。
2. 带通滤波器（BPF）

由低通滤波器和高通滤波器串联组成（ f p 1 f_{p1} fp1 高通截止频率 < f p 2 < f_{p2} <fp2 低通截止频率）。

（1）压控电压源二阶带通滤波器

核心参数：
A u p = Q A u f , f 0 = 1 2 π R C , f b w = f 0 Q A_{up} = Q A_{uf}, \quad f_0 = \frac{1}{2\pi RC}, \quad f_{bw} = \frac{f_0}{Q} Aup=QAuf,f0=2πRC1,fbw=Qf0

  • A u f = 1 + R f R 1 A_{uf} = 1 + \frac{R_f}{R_1} Auf=1+R1Rf（同相比例放大倍数）；
  • Q = 1 3 − A u f Q = \frac{1}{3 - A_{uf}} Q=3−Auf1（品质因数， Q Q Q 越大，通带越窄）。
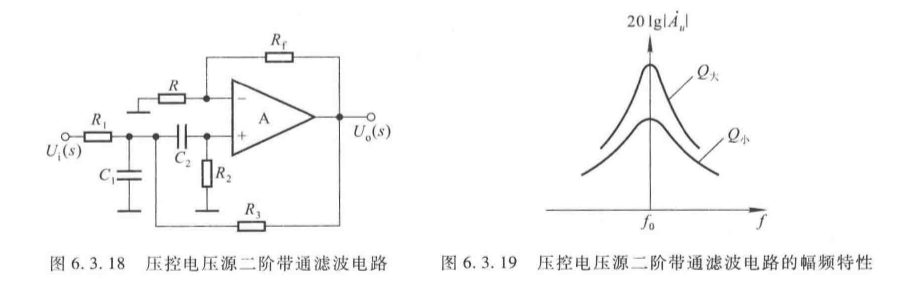
3. 带阻滤波器（BEF）

由低通滤波器和高通滤波器并联后求和组成（ f p 1 f_{p1} fp1 高通截止频率 > f p 2 > f_{p2} >fp2 低通截止频率）。

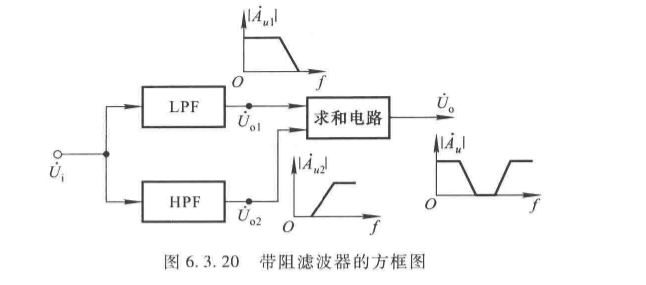
（1）双T网络有源带阻滤波器

核心参数：
f 0 = 1 2 π R C , f b w = f 0 Q , Q = 1 2 ∣ 2 − A u p ∣ f_0 = \frac{1}{2\pi RC}, \quad f_{bw} = \frac{f_0}{Q}, \quad Q = \frac{1}{2|2 - A_{up}|} f0=2πRC1,fbw=Qf0,Q=2∣2−Aup∣1

  • 通带放大倍数 A u p = 1 + R f R 1 A_{up} = 1 + \frac{R_f}{R_1} Aup=1+R1Rf。
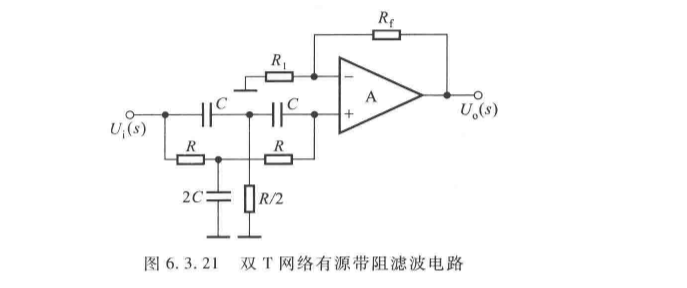
4. 开关电容滤波器

利用"开关电容等效电阻"原理（ R ≈ 1 f c C R \approx \frac{1}{f_c C} R≈fcC1， f c f_c fc 为时钟频率），解决集成大电阻难以制作的问题，核心参数：
f p = C 1 C 2 f c (6.3.44) f_p = \frac{C_1}{C_2} f_c \tag{6.3.44} fp=C2C1fc(6.3.44)

  • 特点：截止频率由时钟频率 f c f_c fc 和电容比 C 1 / C 2 C_1/C_2 C1/C2 决定，精度高、体积小。
5. 状态变量型滤波器

由比例、积分、求和电路组成，可通过外接电阻实现低通、高通、带通、带阻四种滤波功能，性能稳定，调整方便。

6.3.4 滤波电路的选型原则

  1. 根据有用信号和干扰信号的频段选择滤波器类型（LPF/HPF/BPF/BEF）；
  2. 根据选择性要求选择阶数（阶数越高，过渡带越窄，但稳定性越差）；
  3. 根据幅频特性平坦度选择类型（巴特沃斯：幅频平坦；切比雪夫：选择性优；贝塞尔：相位线性）。

6.4 电子信息系统预处理中所用放大电路

在电子信息系统中，传感器输出信号通常微弱、含噪声且源阻抗高，需经预处理放大电路调理后再进行运算或滤波。

6.4.1 仪表放大器

1. 核心特点
  • 高输入电阻（ R i > 10 9 Ω R_i > 10^9 \Omega Ri>109Ω）：适配高阻抗传感器；
  • 高共模抑制比（ K C M R > 100   dB K_{CMR} > 100 \, \text{dB} KCMR>100dB）：抑制环境共模干扰（如电网50Hz干扰）；
  • 低失调电压和温漂：保证微弱信号放大精度；
  • 可调增益：通过外接电阻调整放大倍数。
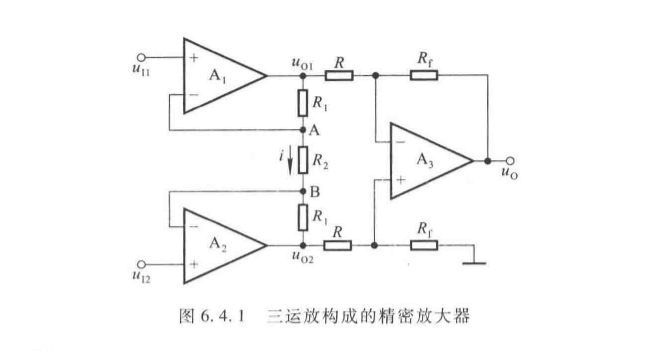
2. 基本电路（三运放结构）
  • 第一级：双运放同相放大，增益 A u 1 = 1 + 2 R 1 R 2 A_{u1} = 1 + \frac{2R_1}{R_2} Au1=1+R22R1；
  • 第二级：差分放大，增益 A u 2 = − R f R A_{u2} = -\frac{R_f}{R} Au2=−RRf；
  • 总增益： A u = A u 1 ⋅ A u 2 = − R f R ( 1 + 2 R 1 R 2 ) A_u = A_{u1} \cdot A_{u2} = -\frac{R_f}{R} \left(1 + \frac{2R_1}{R_2}\right) Au=Au1⋅Au2=−RRf(1+R22R1)。
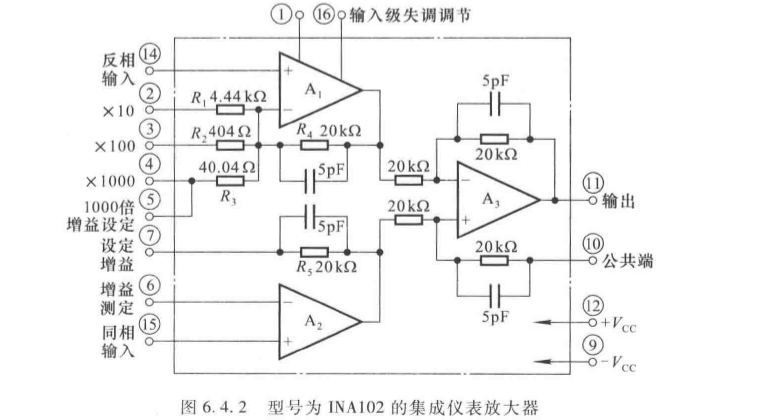
3. 集成仪表放大器（如INA102）
  • 增益可通过引脚连接设定（1、10、100、1000四挡）；
  • 应用：压力、温度传感器信号放大，数据采集系统前端。

6.4.2 电荷放大器

1. 核心应用

适配电容性传感器（如压电式加速度传感器、压力传感器），将传感器输出的电荷量转换为电压。

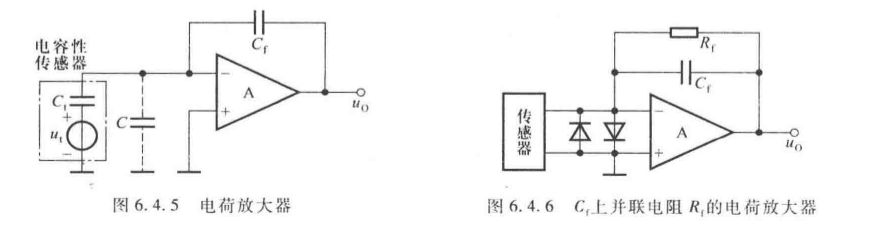
2. 基本电路
  • 运算关系（理想运放）：
    u O = − q C f (6.4.5) u_O = -\frac{q}{C_f} \tag{6.4.5} uO=−Cfq(6.4.5)
    其中 q q q 为传感器输出电荷量， C f C_f Cf 为反馈电容；
  • 实用电路：在 C f C_f Cf 并联电阻 R f R_f Rf，防止运放因长时间充电饱和。

6.4.3 隔离放大器

1. 核心功能

切断输入侧与输出侧的电气连接，抑制共模干扰和高压窜扰，保障人身和设备安全。

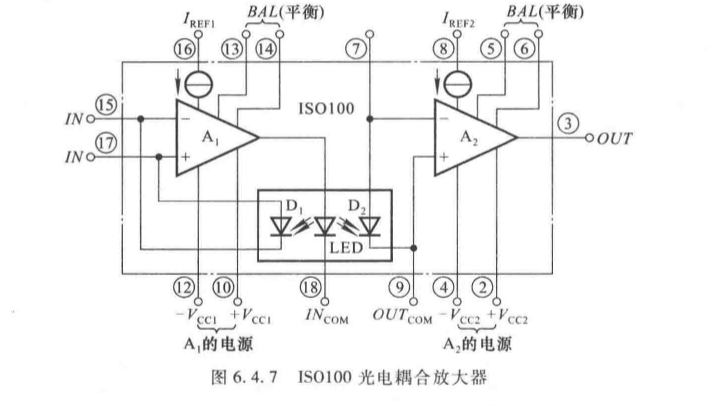
2. 类型与原理
  • 光电耦合型（如ISO100）：通过光信号传递信号，输入输出电气隔离；
  • 核心关系： u O = R f R u I u_O = \frac{R_f}{R} u_I uO=RRfuI（ D 1 D_1 D1、 D 2 D_2 D2 光电二极管特性对称）；
  • 应用：工业控制、医疗设备、高压环境下的信号放大。

6.4.4 干扰和噪声的抑制措施

1. 干扰来源
  • 外部干扰：电网50Hz干扰、电磁波辐射、电源噪声；
  • 内部噪声：电阻热噪声、晶体管散弹噪声、1/f噪声。
2. 抑制措施
  • 屏蔽：用金属屏蔽罩隔离辐射干扰；
  • 滤波：电源端加去耦电容（10~30μF钽电容+0.1μF独石电容），信号通路加有源滤波电路；
  • 接地：采用单点接地，避免地环路干扰；
  • 选型：选用低噪声运放、金属膜电阻，减小内部噪声。

6.5 Multisim应用举例（核心结论）

  1. 运算电路求解方程 ：利用乘法器、加法器搭建方程对应的运算电路，通过直流扫描可求解一元二次方程（如 2 X 2 + X − 6 = 0 2X^2 + X - 6 = 0 2X2+X−6=0 的解为 X = 1.5 X=1.5 X=1.5 和 X = − 2 X=-2 X=−2）；
  2. 滤波电路幅频特性测试 ：通过波特图仪测量压控电压源二阶低通滤波器的幅频特性，验证 Q Q Q 值对选择性的影响（ Q Q Q 越大， f 0 f_0 f0 附近幅值越大）。

本章小结

核心知识点梳理

  1. 基本运算电路：

    • 核心分析工具：理想运放"虚短"（ u P = u N u_P = u_N uP=uN）和"虚断"（ i P = i N = 0 i_P = i_N = 0 iP=iN=0）；
    • 关键电路：比例（反相/同相/跟随器）、加减（反相/同相/差分）、积分/微分、对数/指数，核心是推导运算关系并理解参数影响；
    • 误差来源：运放非理想特性（ A o d A_{od} Aod、 K C M R K_{CMR} KCMR、失调参数），需选用高精度运放。

  2. 模拟乘法器应用：

    • 核心功能： u O = k u X u Y u_O = k u_X u_Y uO=kuXuY，实现乘方、除法、开方、二倍频运算；
    • 关键：保证负反馈，避免自激或闭锁。

  3. 有源滤波电路：

    • 分类：低通、高通、带通、带阻，核心参数为 A u p A_{up} Aup、 f p f_p fp、 Q Q Q、过渡带斜率；
    • 分析方法：传递函数→频率特性，阶数越高选择性越好，但稳定性需权衡；
    • 特殊类型：开关电容滤波器（集成化）、状态变量型滤波器（多功能）。

  4. 预处理放大电路：

    • 仪表放大器：高 R i R_i Ri、高 K C M R K_{CMR} KCMR，适配传感器微弱信号；
    • 电荷放大器：适配电容性传感器；
    • 隔离放大器：抑制共模干扰，保障安全。

核心能力要求

  1. 会识别：区分运算电路和滤波电路的类型及功能；
  2. 会推导：根据"虚短""虚断"推导运算关系或传递函数；
  3. 会选型：根据需求选择运算电路、滤波电路类型及运放型号；
  4. 会抑制：掌握干扰和噪声的抑制措施，提高电路精度。
相关推荐
virtual_k1smet2 小时前
梧桐·鸿鹄-中移链assistant-level
笔记·区块链
丝斯20113 小时前
AI学习笔记整理（36）——自然语言处理
人工智能·笔记·学习
94621931zyn63 小时前
观影统计 - Cordova 与 OpenHarmony 混合开发实战
笔记
virtual_k1smet4 小时前
梧桐·鸿鹄-大数据professional
大数据·笔记
stars-he4 小时前
单相双半波可控整流电路的MATLAB仿真设计
笔记·学习·matlab
im_AMBER4 小时前
Leetcode 87 等价多米诺骨牌对的数量
数据结构·笔记·学习·算法·leetcode
今儿敲了吗4 小时前
计算机网络第一章笔记
笔记·计算机网络
yuxb735 小时前
Jenkins 流水线：镜像仓库与自动化部署
笔记·jenkins
YJlio5 小时前
Sysinternals 磁盘工具学习笔记（13.0）：从 VHD 备份到碎片整理与卷标管理总览
服务器·笔记·学习
热门推荐
01GitHub 镜像站点02从快手“12·22”直播攻击事件看：一次教科书式的业务层饱和攻击033D 圣诞树网页代码04电脑检测软件—图吧工具箱05Linux下V2Ray安装配置指南06UV安装并设置国内源07在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）08jdk21下载、安装（Windows、Linux、macOS）09Gemini3 生成的基于手势控制3D粒子圣诞树10Claude Code Skills 实用使用手册