2、OpenCV Harris角点检测笔记

一、Harris角点检测原理

1. 基本思想

通过移动检测窗口，观察窗口内像素值的变化情况来判断是否为角点：

2. 三种检测情况

情况	窗口移动方向	像素变化	判断结果	示意图
平坦区域	任何方向移动	无变化	非角点	窗口在任何方向移动，像素值不变
边缘区域	沿边缘方向移动	无变化	边缘	沿边缘平行移动不变，垂直移动有变化
角点区域	任何方向移动	都有变化	角点	所有方向移动都会引起像素值变化

3. 数学原理简化

计算窗口内像素值变化量：E(u,v) = Σ w(x,y)[I(x+u,y+v)-I(x,y)]²
使用泰勒展开和矩阵运算，最终得到角点响应函数：
R = det(M) - k·(trace(M))²
- det(M)：矩阵M的行列式
- trace(M)：矩阵M的迹
- k：经验常数（0.02-0.04）

二、OpenCV Harris角点检测API

函数原型

python 复制代码

dst = cv2.cornerHarris(src, blockSize, ksize, k[, dst[, borderType]])

参数详解

参数	类型	说明
`src`	输入图像	必须是灰度图（单通道8位或浮点型）
`blockSize`	int	检测窗口大小（邻域大小）
`ksize`	int	Sobel算子的卷积核大小（必须为奇数）
`k`	float	角点检测方程中的自由参数，经验值范围：0.02-0.04
`dst`	输出图像	存储角点检测结果的图像（通常与输入图像同大小）
`borderType`	int	边界填充类型（可选，默认`cv2.BORDER_DEFAULT`）

关键点说明

输入图像必须为灰度图 ：检测前需使用cv2.cvtColor()转换
blockSize大小影响：值越大，检测的角点越少但更显著
ksize通常设为3：Sobel算子卷积核大小
k值经验性：推荐0.04，可根据实际效果调整

三、代码实现步骤

1. 基本流程

python 复制代码

import cv2
import numpy as np

# 1. 读取图像
img = cv2.imread('chess.png')

# 2. 转换为灰度图
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

# 3. Harris角点检测
blockSize = 2     # 检测窗口大小
ksize = 3         # Sobel卷积核大小
k = 0.04          # 经验参数
dst = cv2.cornerHarris(gray, blockSize, ksize, k)

# 4. 标记角点（在原图上显示）
# 角点响应值大于最大响应值的1%时标记为红色
img[dst > 0.01 * dst.max()] = [0, 0, 255]  # BGR格式：红色

# 5. 显示结果
cv2.imshow('Harris Corners', img)
cv2.waitKey(0)
cv2.destroyAllWindows()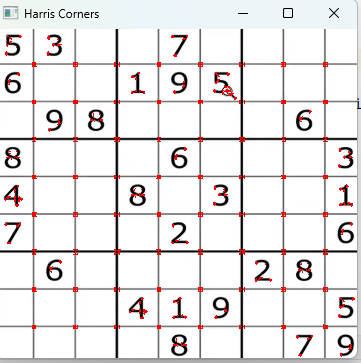

2. 参数调整技巧

增加blockSize：检测更显著的角点，但可能漏掉细节
调整k值 ：
- 增大k值（接近0.04）：减少角点数量
- 减小k值（接近0.02）：增加角点数量
阈值调整 ：0.01 * dst.max()中的系数可调，影响角点数量

四、实际应用注意事项

1. 图像预处理

可先进行高斯模糊减少噪声干扰：cv2.GaussianBlur()
确保图像有足够对比度

2. Harris角点检测的优缺点

优点：

计算简单，实时性较好
对图像旋转、亮度变化具有一定不变性
对噪声有一定鲁棒性

缺点：

对尺度变化敏感（缩放后角点可能变化）
k值为经验参数，需要调整
只能检测角点，不能获取角点描述符（无法用于匹配）

3. 与后续学习的关联

Harris是基础角点检测方法
后续将学习更先进的SIFT、SURF、ORB等特征检测算法
理解Harris有助于理解更复杂算法的原理

五、总结要点

Harris检测原理：通过检测窗口移动时像素值的变化模式判断角点
三种区域类型：平坦区域、边缘区域、角点区域
API关键参数 ：
- blockSize：检测窗口大小
- ksize：Sobel卷积核大小（通常为3）
- k：经验参数（0.02-0.04，常用0.04）
必须步骤：输入图像需转换为灰度图
结果显示：通过阈值筛选显著角点并在原图标记

学习建议 ：理解原理后，尝试调整参数观察角点检测效果的变化，特别是blockSize和k值对结果的影响，为后续学习更复杂的特征检测算法打下基础。