目录
- 前言
- [1. RM 算法 (Robbins-Monro)](#1. RM 算法 (Robbins-Monro))
-
- [1.1 定义与分析](#1.1 定义与分析)
- [1.2 应用实例:求期望值](#1.2 应用实例:求期望值)
- [2. 梯度下降](#2. 梯度下降)
-
- [2.1 随机梯度下降 (Stochastic Gradient Descent, SGD)](#2.1 随机梯度下降 (Stochastic Gradient Descent, SGD))
- [2.2 批量梯度下降 (Batch Gradient Descent, BGD)](#2.2 批量梯度下降 (Batch Gradient Descent, BGD))
- [2.3 小批量梯度下降 (Mini-Batch Gradient Descent, MBGD)](#2.3 小批量梯度下降 (Mini-Batch Gradient Descent, MBGD))
- [3. 另一角度认识梯度下降](#3. 另一角度认识梯度下降)
前言
本文内容主要参考《赵世钰. 强化学习的数学原理》 整理编写,本文也加入了许多自己的认识,详细内容请参见教材,致谢 赵世钰 老师 和 GPT。
1. RM 算法 (Robbins-Monro)
1.1 定义与分析
针对标量方程:
g ( ω ) = 0 (1.1) g(\omega) =0 \tag{1.1} g(ω)=0(1.1)
当输入 ω \omega ω 时,可观测输出值:
g ~ ( ω , η ) = g ( ω ) + η \tilde{g}(\omega, \eta) = g(\omega) + \eta g~(ω,η)=g(ω)+η
其中 η \eta η 为观测噪声。
存在算法:
ω k + 1 = ω k − α k g ~ ( ω k , η k ) (1.2) \omega_{k+1} = \omega_k - \alpha_k \tilde{g}(\omega_k, \eta_k) \tag{1.2} ωk+1=ωk−αkg~(ωk,ηk)(1.2)
当满足以下条件时, ω k \omega_{k} ωk 几乎必然收敛到方程 ( 1.1 ) (1.1) (1.1) 的根:
(1). 0 < ∇ g ( ω ) < ∞ 0 < \nabla{g}(\omega) < \infty 0<∇g(ω)<∞
(2). ∑ k = 1 ∞ a k = ∞ \sum^\infty_{k=1} a_k = \infty ∑k=1∞ak=∞
(3). ∑ k = 1 ∞ a k 2 < ∞ \sum^\infty_{k=1} a^2_k < \infty ∑k=1∞ak2<∞,可理解为 lim k → ∞ a k → 0 \displaystyle \lim_{k \to \infty} a_k \to 0 k→∞limak→0
(4). 对任意 ω \omega ω, E ( η ) = 0 \mathbb{E}(\eta) = 0 E(η)=0 且 E ( η 2 ) < ∞ \mathbb{E}(\eta^2) < \infty E(η2)<∞
例:求解 g ( ω ) = tanh ( ω − 1 ) = 0 g(\omega)=\tanh{(\omega -1)}=0 g(ω)=tanh(ω−1)=0,取 ω 1 = 3 \omega_1 = 3 ω1=3, a k = 1 / k a_k = 1/k ak=1/k
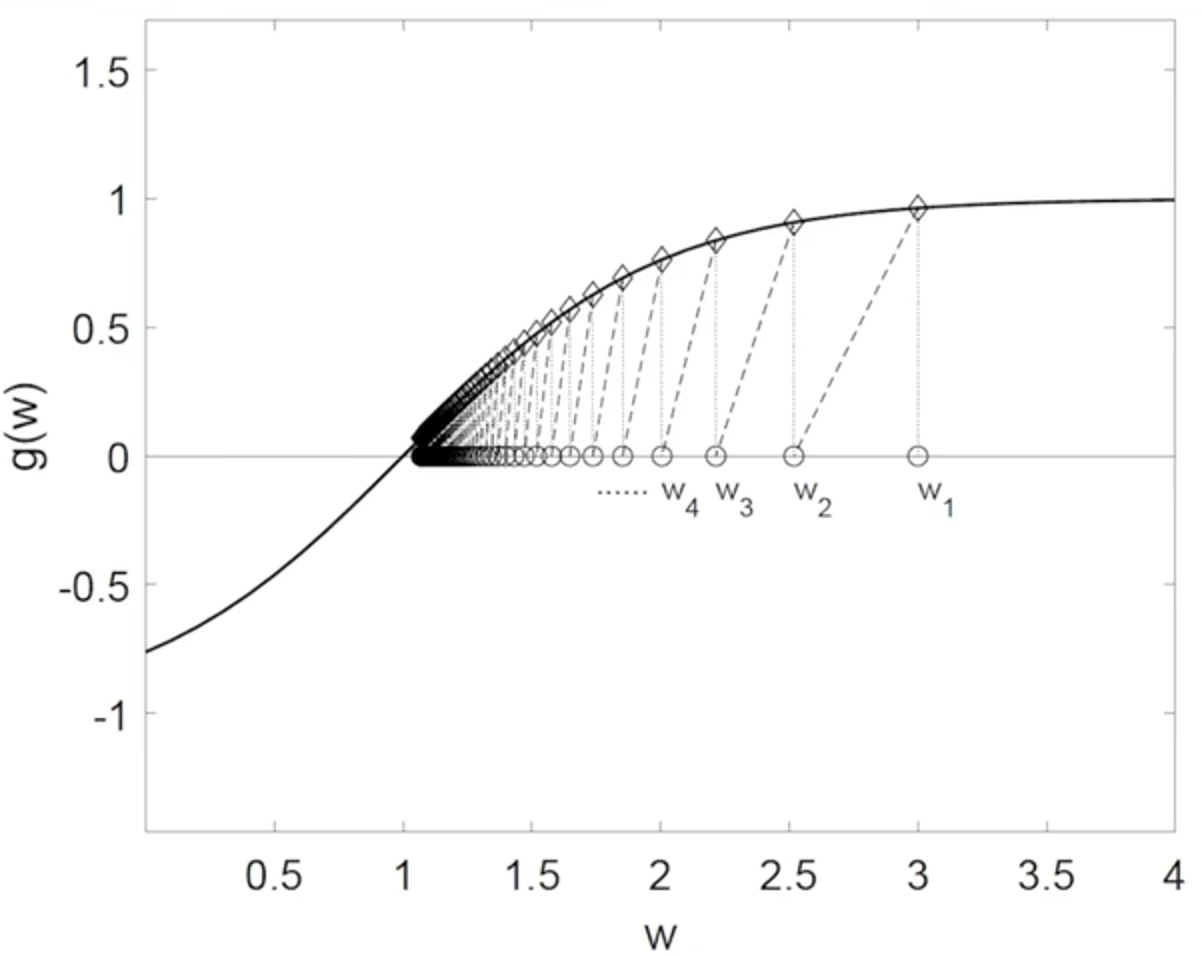
收敛的直观理解:
函数 g ( ω ) g(\omega) g(ω) 是单调递增的,函数与 x x x 轴有交点,交点即为目标解 ω ∗ \omega^* ω∗;
当 ω k > ω ∗ \omega_k>\omega^* ωk>ω∗, g ( ω ) > 0 g(\omega) > 0 g(ω)>0, − α k g ( ω k ) -\alpha_k g(\omega_k) −αkg(ωk) 将令 ω k + 1 \omega_{k+1} ωk+1 减小;
当 ω k < ω ∗ \omega_k<\omega^* ωk<ω∗, g ( ω ) < 0 g(\omega) < 0 g(ω)<0, − α k g ( ω k ) -\alpha_k g(\omega_k) −αkg(ωk) 将令 ω k + 1 \omega_{k+1} ωk+1 增大;
并且,条件 (1)(3) 要求 ▽ g ( ω ) < ∞ \bigtriangledown{g}(\omega) < \infty ▽g(ω)<∞,而 lim k → ∞ a k → 0 \displaystyle \lim_{k \to \infty} a_k \to 0 k→∞limak→0,使得 α k g ( ω k ) → 0 \alpha_k g(\omega_k) \to 0 αkg(ωk)→0,使 ω k \omega_k ωk 趋于收敛。
其实当不满足 α k g ( ω k ) → 0 \alpha_k g(\omega_k) \to 0 αkg(ωk)→0 但 α k \alpha_k αk 趋于小值时, ω k \omega_k ωk 也将在 ω ∗ \omega^* ω∗ 附近抖动,收敛于一定范围;
这样的结果也是常用的, α k \alpha_k αk 不趋于 0 0 0,使得 k k k 较大时的数据样本仍然作用,可应对时变系统 g ( ω , t ) g(\omega,t) g(ω,t)。
结合例子,可 直观感受 RM 算法条件的作用:
- 条件 (1) 要求 g ( ω ) g(\omega) g(ω) 是单调的,若 g ( ω ) g(\omega) g(ω) 是单调递减的,可取 − g ( ω ) -g(\omega) −g(ω)
- 条件 (2) 要求 α k \alpha_k αk 不能太快收敛到 0 0 0,否则不能保证任意初始值可收敛到解 ω ∗ \omega^* ω∗:
根据式 ( 1.2 ) (1.2) (1.2) 有:
ω 2 − ω 1 = − α 1 g ~ ( ω 1 , η 1 ) ω 3 − ω 2 = − α 2 g ~ ( ω 2 , η 2 ) ⋮ \begin{align*} \omega_2 - \omega_1 &= -\alpha_1\tilde{g}(\omega_1, \eta_1) \\ \omega_3 - \omega_2 &= -\alpha_2\tilde{g}(\omega_2, \eta_2) \\ &\vdots \end{align*} ω2−ω1ω3−ω2=−α1g~(ω1,η1)=−α2g~(ω2,η2)⋮
累加得:
ω ∞ − ω 1 = − ∑ k = 1 ∞ α k g ~ ( ω k , η k ) \omega_\infty - \omega_1 = -\sum_{k=1}^\infty \alpha_k\tilde{g}(\omega_k, \eta_k) ω∞−ω1=−k=1∑∞αkg~(ωk,ηk)
若 ∑ k = 1 ∞ a k < ∞ \sum^\infty_{k=1} a_k < \infty ∑k=1∞ak<∞,则可能存在上界 ∣ ∑ k = 1 ∞ α k g ~ ( ω k , η k ) ∣ < b |\sum_{k=1}^\infty \alpha_k\tilde{g}(\omega_k, \eta_k)|<b ∣∑k=1∞αkg~(ωk,ηk)∣<b
当选取的初始值离解 ω ∗ \omega^* ω∗ 过远,即 ∣ ω 1 − ω ∗ ∣ > b |\omega_1 - \omega^*| > b ∣ω1−ω∗∣>b 时, ω ∞ \omega_\infty ω∞ 无法收敛至 ω ∗ \omega^* ω∗ - 条件 (3) 要求 lim k → ∞ a k → 0 \displaystyle \lim_{k \to \infty} a_k \to 0 k→∞limak→0,结合条件 (1) 要求 ▽ g ( ω ) < ∞ \bigtriangledown{g}(\omega) < \infty ▽g(ω)<∞,得 α k g ~ ( ω k , η k ) → 0 \alpha_k \tilde{g}(\omega_k, \eta_k) \to 0 αkg~(ωk,ηk)→0,使得 ω k \omega_k ωk 趋于收敛;但实际中,小范围的波动的次优解也常被接受
- 条件 (4) 为对噪声的要求
RM 算法理论证明可参见原书教材。
1.2 应用实例:求期望值
在蒙特卡洛方法中,使用数据样本来求贝尔曼方程中所需的期望值,如贝尔曼方程:
v π ( s k ) ' = E ( r k + 1 + γ v π ( s k + 1 ) ↦ E ( x k ) \begin{align*} v_\pi(s_k) `&= \mathbb{E}(r_{k+1} + \gamma v_{\pi}(s_{k+1}) \\ &\mapsto \mathbb{E}(x_k) \end{align*} vπ(sk)'=E(rk+1+γvπ(sk+1)↦E(xk)
其中 x k = r k + 1 + γ ( r k + 2 + γ r k + 3 + ⋯ ) x_k = r_{k+1} + \gamma(r_{k+2} + \gamma r_{k+3} + \cdots) xk=rk+1+γ(rk+2+γrk+3+⋯)
根据大数定律,有大量样本( N N N 个)时,可计算为:
E ( x k ) ≈ E ( x k ) N = 1 N ∑ i = 1 N x k , i (1.3) \mathbb{E}(x_k) \approx \mathbb{E}(x_k)N = \frac{1}{N} \sum{i=1}^N x_{k,i} \tag{1.3} E(xk)≈E(xk)N=N1i=1∑Nxk,i(1.3)
当所有样本不是立即获得时,可转为增量计算,有:
E ( x k ) N + 1 = 1 N + 1 [ ( N + 1 − 1 ) ⋅ E ( x k ) N + x k , N + 1 ] = E ( x k ) N + 1 N + 1 ( x k , N + 1 − E ( x k ) N ) (1.4) \begin{align*} \mathbb{E}(x_k)_{N+1} &= \frac{1}{N+1} \left[ (N+1 -1) \cdot \mathbb{E}(x_k)N + x{k,N+1}\right] \\ &= \mathbb{E}(x_k)N + \frac{1}{N+1}(x{k,N+1} - \mathbb{E}(x_k)_N) \end{align*} \tag{1.4} E(xk)N+1=N+11[(N+1−1)⋅E(xk)N+xk,N+1]=E(xk)N+N+11(xk,N+1−E(xk)N)(1.4)
随着 N N N 的增加,结果也将趋于真实期望值
式 ( 1.4 ) (1.4) (1.4) 中增量计算的形式可由 RM 算法得到:
定义目标方程:
g ( ω ) = ω − E ( x k ) = 0 (1.5) g(\omega) = \omega - \mathbb{E}(x_k)=0 \tag{1.5} g(ω)=ω−E(xk)=0(1.5)
当 E ( x k ) \mathbb{E}(x_k) E(xk) 不可观测,可观测值为 x k , i = E ( x k ) + η i x_{k,i} = \mathbb{E}(x_k) + \eta_i xk,i=E(xk)+ηi,其中 η i \eta_i ηi 为噪声,故函数观测值为:
g ~ ( ω , η i ) = ω − x k , i = ω − E ( x k ) + η i = g ( ω ) + η i \begin{align*} \tilde{g}(\omega,\eta_i) &= \omega - x_{k,i} \\ &=\omega - \mathbb{E}(x_k) + \eta_i \\ &=g(\omega) + \eta_i \end{align*} g~(ω,ηi)=ω−xk,i=ω−E(xk)+ηi=g(ω)+ηi
根据 RM 算法,方程 ( 1.5 ) (1.5) (1.5) 可求解为:
ω i + 1 = ω i − α i g ~ ( ω , η i ) = ω i − α i ( ω i − x k , i ) \begin{align*} \omega_{i+1} &= \omega_i - \alpha_i\tilde{g}(\omega,\eta_i) \\ &=\omega_i - \alpha_i ( \omega_i - x_{k,i} ) \end{align*} ωi+1=ωi−αig~(ω,ηi)=ωi−αi(ωi−xk,i)
当 α i = 1 / ( i + 1 ) \alpha_i = 1/(i+1) αi=1/(i+1) 时,满足 RM 算法条件,且上式与 ( 1.5 ) (1.5) (1.5) 一致,可得:
ω i → E ( x k ) \omega_i \to \mathbb{E}(x_k) ωi→E(xk)
2. 梯度下降
下面将使用 RM 算法推导梯度下降:
在只考虑标量下,针对优化问题:
ω ∗ = arg min ω J ( ω ) \omega^* = \arg \min_{\omega} J(\omega) ω∗=argωminJ(ω)
当函数二阶导数 ∇ 2 J ( ω ) > 0 \nabla^2 J(\omega) >0 ∇2J(ω)>0 时,在 ∇ J ( ω ) = 0 \nabla J(\omega) =0 ∇J(ω)=0 处,函数具有最小值。
当系统模型已知时, ∇ J ( ω ) = 0 \nabla J(\omega) =0 ∇J(ω)=0 可尝试直接推导求解析解,
但当系统过于复杂或未知时,可使用 RM 算法,通过数据求数值解:
定义目标方程:
g ( ω ) = ∇ J ( ω ) = 0 g(\omega) = \nabla J(\omega) =0 g(ω)=∇J(ω)=0
当可准确计算梯度时,观测方程为:
g ~ ( ω , η ) = ∇ J ( ω ) \tilde{g}(\omega, \eta) =\nabla J(\omega) g~(ω,η)=∇J(ω)
根据 RM 算法数值解可得梯度下降算法:
ω k + 1 = ω k − α k ∇ J ( ω k ) (2.1) \omega_{k+1} = \omega_k - \alpha_k \nabla J(\omega_k) \tag{2.1} ωk+1=ωk−αk∇J(ωk)(2.1)
同时 RM 算法条件也暗示着对梯度下降的要求:
- 当满足 ▽ g ( ω ) = ▽ 2 J ( ω ) > 0 \bigtriangledown g(\omega) =\bigtriangledown^2 J(\omega) >0 ▽g(ω)=▽2J(ω)>0 时(多维时变为 Hessian 矩阵整个定义域半正定或正定(函数凸)),可找到全局最小值,否则可能陷入局部最优
- α k \alpha_k αk 应逐渐收敛,但也不能收敛太快,梯度下降时一般不收敛至 0
以上可扩展到 n n n 维向量 ω ∈ R n \omega \in \mathbb{R}^n ω∈Rn 时仍可适用.
当梯度不能被准确计算时,RM 算法也暗示着可使用梯度的近似估计值代替真实梯度,即:
g ~ ( ω , ξ ) = ∇ J ( ω ) + η ( ξ ) \tilde{g}(\omega, \xi) = \nabla J(\omega) + \eta(\xi) g~(ω,ξ)=∇J(ω)+η(ξ)
其中噪声 E [ η ( ξ ) ] = 0 \mathbb{E} \left[ \eta (\xi) \right] = 0 E[η(ξ)]=0。
在实际应用中,需优化的损失函数 J ( θ , x , y ) J(\theta,x,y) J(θ,x,y) 往往包含 可计算梯度的模型 f θ ( x ) f_\theta(x) fθ(x) 和 样本数据 y ( x ) y(x) y(x),使用梯度下降优化参数可表达为:
θ ∗ = arg min θ J ( θ , x , y ) \theta^* = \arg \min_{\theta} J(\theta,x,y) θ∗=argθminJ(θ,x,y)
一般可设 J ( θ , x , y ) = 1 2 ( ∣ ∣ f θ ( x ) − y ( x ) ∣ ∣ 2 ) 2 J(\theta,x,y) = \frac{1}{2} \big(|| f_\theta(x) - y(x) ||_2 \big) ^2 J(θ,x,y)=21(∣∣fθ(x)−y(x)∣∣2)2.
梯度下降的表达形式为:
θ k + 1 = θ k − α k ∇ θ J ( θ k , x , y ) \theta_{k+1} = \theta_k - \alpha_k \nabla_\theta J(\theta_k,x,y) θk+1=θk−αk∇θJ(θk,x,y)
其中 θ \theta θ、 x x x、 y y y 可以是多维的, J ( ⋅ ) : R n ↦ R J(\cdot): \mathbb{R}^n \mapsto \mathbb{R} J(⋅):Rn↦R.
理想的梯度为:
∇ θ J k = [ ∂ J k ∂ θ ( 1 ) , ∂ J k ∂ θ ( 2 ) , ⋯ , ∂ J k ∂ θ ( n ) ] T \nabla_\theta J_k = [\frac{\partial{J_k}}{\partial{\theta_{(1)}}},\ \frac{\partial{J_k}}{\partial{\theta_{(2)}}},\ \cdots,\ \frac{\partial{J_k}}{\partial{\theta_{(n)}}}]^T ∇θJk=[∂θ(1)∂Jk, ∂θ(2)∂Jk, ⋯, ∂θ(n)∂Jk]T
上式表示了 J ( θ k , x , y ) J(\theta_k,x,y) J(θk,x,y) 在 ( θ k , x , y ) (\theta_k,x,y) (θk,x,y) 处沿 θ \theta θ 各维度的的变化率。
但由于随机样本数据 ( x , y ) (x,y) (x,y) 的引入,真实优化目标的梯度是期望梯度:
∇ θ J k = E ( x , y ) ( ∇ θ l ( θ ; x , y ) ) \nabla_\theta J_k = \mathbb{E}{(x,y)}(\nabla\theta \mathcal{l}(\theta;x,y)) ∇θJk=E(x,y)(∇θl(θ;x,y))
其中 l ( θ ; x , y ) \mathcal{l}(\theta;x,y) l(θ;x,y) 为单样本损失函数
针对单一样本 ( x i , y i ) (x_i, y_i) (xi,yi),单一样本梯度为:
∇ θ , 1 J k = ∇ θ l ( θ ; x i , y i ) (2.2) \nabla_{\theta,1} J_k = \nabla_\theta \mathcal{l}(\theta;x_i,y_i) \tag{2.2} ∇θ,1Jk=∇θl(θ;xi,yi)(2.2)
N N N 样本梯度为:
∇ θ , N J k = 1 N ∑ i = 1 N ∇ θ l ( θ ; x i , y i ) (2.3) \nabla_{\theta,N} J_k = \frac{1}{N}\sum_{i=1}^N\nabla_\theta \mathcal{l}(\theta;x_i,y_i) \tag{2.3} ∇θ,NJk=N1i=1∑N∇θl(θ;xi,yi)(2.3)
当 N → ∞ N \to \infty N→∞, ∇ θ , N J k → E ( x , y ) ( ∇ θ l ( θ ; x , y ) ) \nabla_{\theta,N} J_k \to \mathbb{E}{(x,y)}(\nabla\theta \mathcal{l}(\theta;x,y)) ∇θ,NJk→E(x,y)(∇θl(θ;x,y))
由此也区分出了随机梯度下降、小批量梯度下降和批量梯度下降.
2.1 随机梯度下降 (Stochastic Gradient Descent, SGD)
当使用单个样本进行梯度下降时,即为随机梯度下降:
θ k + 1 = θ k − α k ∇ θ , 1 J k \theta_{k+1} = \theta_k - \alpha_k \nabla_{\theta,1} J_k θk+1=θk−αk∇θ,1Jk
单个样本时,样本方差最大,但 RM 算法也揭示了,无偏估计下有限的噪声不影响收敛
2.2 批量梯度下降 (Batch Gradient Descent, BGD)
当拥有 N N N 个样本,同时计算进行梯度下降时,即为批量梯度下降:
θ k + 1 = θ k − α k ∇ θ , N J k \theta_{k+1} = \theta_k - \alpha_k \nabla_{\theta,N} J_k θk+1=θk−αk∇θ,NJk
当 N → ∞ N \to \infty N→∞, ∇ θ , N J k → E ( ∇ θ J k ) \nabla_{\theta,N} J_k \to \mathbb{E}(\nabla_\theta J_k) ∇θ,NJk→E(∇θJk)
2.3 小批量梯度下降 (Mini-Batch Gradient Descent, MBGD)
当拥有 N N N 个样本,可仅随机选取小批量的 M M M 个样本进行计算,即为小批量梯度下降:
θ k + 1 = θ k − α k ∇ θ , M J k \theta_{k+1} = \theta_k - \alpha_k \nabla_{\theta,M} J_k θk+1=θk−αk∇θ,MJk
小批量通过对梯度取均值降低方差,使更新方向更接近期望梯度,从而在稳定性与效率之间取得折中;
选择小批量梯度下降的优势在于:
以增加每次迭代的计算开销为代价,显著降低梯度噪声,从而减少参数更新中的震荡与不稳定性。
在实际深度学习中,选择 MBGD 还有一个决定性原因:
现代硬件(GPU/TPU)对批量计算高度友好
batch 太小 → 硬件利用率低
batch 太大 → 梯度"过平滑"、泛化变差
3. 另一角度认识梯度下降
针对优化问题:
ω ⃗ ∗ = arg min ω ⃗ J ( ω ⃗ ) \vec{\omega}^* = \arg \min_{\vec{\omega}} J(\vec{\omega}) ω ∗=argω minJ(ω )
在 ω ⃗ k \vec{\omega}_k ω k 处使用一阶泰勒展开,并移动小量 ϵ ⃗ \vec{\epsilon} ϵ ,使得可忽略高阶项:
J ( ω ⃗ k + ϵ ⃗ ) ≈ J ( ω ⃗ k ) + ∇ J ( ω ⃗ k ) T ϵ ⃗ J(\vec{\omega}_k + \vec{\epsilon}) \approx J(\vec{\omega}_k) + \nabla J(\vec{\omega}_k)^T\ \vec{\epsilon} J(ω k+ϵ )≈J(ω k)+∇J(ω k)T ϵ
此时,函数值 J ( ω ⃗ ) J(\vec{\omega}) J(ω ) 沿梯度方向 ∇ J ( ω ⃗ k ) \nabla J(\vec{\omega}_k) ∇J(ω k) 变化,
始终可以令 ϵ ⃗ = − α k ∇ J ( ω ⃗ k ) \vec{\epsilon} = -\alpha_k\nabla J(\vec{\omega}_k) ϵ =−αk∇J(ω k),其中满足 α k > 0 \alpha_k>0 αk>0,且 ϵ ⃗ \vec{\epsilon} ϵ 是小量,使近似成立,
从而使得函数值下降:
J ( ω ⃗ k + ϵ ⃗ ) ≈ J ( ω ⃗ k ) − α k ∣ ∣ ∇ J ( ω ⃗ k ) ∣ ∣ 2 J(\vec{\omega}_k + \vec{\epsilon}) \approx J(\vec{\omega}_k) - \alpha_k|| \nabla J(\vec{\omega}_k)||_2 J(ω k+ϵ )≈J(ω k)−αk∣∣∇J(ω k)∣∣2
重复迭代即可使 J ( ω ⃗ ) J(\vec{\omega}) J(ω ) 收敛至局部最小,即:
ω ⃗ k + 1 = ω ⃗ k + ϵ ⃗ = ω ⃗ k − α k ∇ J ( ω ⃗ k ) \begin{align*} \vec{\omega}_{k+1} &= \vec{\omega}_k + \vec{\epsilon} \\ &= \vec{\omega}_k - \alpha_k\nabla J(\vec{\omega}_k) \end{align*} ω k+1=ω k+ϵ =ω k−αk∇J(ω k)
其中, α k \alpha_k αk 常称为学习率,其选择也很讲究。
扩展 : 如果梯度下降对应一阶近似,那牛顿法对应了二阶近似

更高阶的优化方法几乎很少被应用:
