0. 旅行商问题(TSP)定义
1. 问题描述
给定 nnn 个城市及任意两城之间的旅行成本,求一条从起点出发、访问每个城市恰好一次并返回起点的最短回路。该回路称为哈密顿回路。
通常固定起点为城市 000,其余城市 {1,2,...,n−1}\{1,2,\dots,n-1\}{1,2,...,n−1} 的每一种排列对应一条候选路径。
2. 输入与输出
-
输入:
- 城市数 nnn(n≥2n \geq 2n≥2);
- n×nn \times nn×n 成本矩阵 Cost=[cij]\text{Cost} = [c_{ij}]Cost=[cij],其中 cii=0c_{ii} = 0cii=0,cij≥0c_{ij} \geq 0cij≥0。若 cij=cjic_{ij} = c_{ji}cij=cji,称为对称 TSP(即无向图)。
-
输出:
- 最短回路总成本;
- 对应的最优访问序列(如 [0,2,1,3,0][0,2,1,3,0][0,2,1,3,0])。
示例 (n=4n=4n=4):
Cost=(0306430051065020410200) \text{Cost} = \begin{pmatrix} 0 & 30 & 6 & 4 \\ 30 & 0 & 5 & 10 \\ 6 & 5 & 0 & 20 \\ 4 & 10 & 20 & 0 \end{pmatrix} Cost= 0306430051065020410200
3. 约束条件
- 每个城市访问恰好一次;
- 路径必须闭合(起点 = 终点);
- 解空间大小为 (n−1)!(n-1)!(n−1)!(因起点固定,且起点不影响求解)。
一、蛮力算法(暴力枚举)
1. 求解思路
蛮力算法的核心是通过 全排列生成 枚举所有可能的旅行路径,从中找到总距离最短的回路。
- 路径构造 :固定起点(如城市 0),对剩余的 n−1n-1n−1 个城市进行全排列。每一个全排列都代表一种访问顺序。
- 回路闭合:对于每一个生成的排列,计算从起点出发,按排列顺序访问所有城市,最后回到起点的总距离。
- 状态转移与回溯 :利用递归进入深层决策,每一层递归确定路径中的一个位置。
- 交换 (Swap):原地修改数组,避免额外的空间开销。
- 回溯 (Backtracking):在递归返回后恢复数组原始状态,确保能遍历所有可能的分支。
- 最优解更新:维护全局变量,记录当前已发现的最短距离及对应的路径序列。
2. 递归关系式
在基于交换的全排列生成过程中,假设 SolveTSP(k)SolveTSP(k)SolveTSP(k) 表示从第 kkk 个位置开始对剩余城市进行处理的逻辑:
SolveTSP(k)={计算当前完整路径的总距离if k=n−1∑i=kn−1(swap(k,i)+SolveTSP(k+1)+swap(k,i))if k<n−1 \large SolveTSP(k) = \begin{cases} \text{计算当前完整路径的总距离} & \text{if } k = n-1 \\ \sum_{i=k}^{n-1} (\text{swap}(k, i) + SolveTSP(k+1) + \text{swap}(k, i)) & \text{if } k < n-1 \end{cases} SolveTSP(k)=⎩ ⎨ ⎧计算当前完整路径的总距离∑i=kn−1(swap(k,i)+SolveTSP(k+1)+swap(k,i))if k=n−1if k<n−1
3. 算法伪代码
全局变量定义
minCost←∞\leftarrow \infty←∞ (初始最短路径无穷大)bestPath[n+1](存放最优路径序列)
主函数
c
Function TSP_BF(Cost,n): #Cost矩阵
S <-- Array(n-1) #存放待排列城市{1,...,n-1}
for i <-- 0 to n-2 do
S[i] <-- i+1
end for
Solve_TSP(S, 0, n-1, Cost)
return minCost, bestPath递归子函数
c
Function Solve_TSP(S, k, m, Cost):
#k为当前确定的位置索引,m为数组S的长度(n-1)
if k=m then #递归边界:已生成一个完整排列
currentCost <-- Cost[0][S[0]] #起点0到排列第1个城市距离
for i <-- 0 to m-2 do #累加相邻城市间的距离
currentCost <-- currentCost+Cost[S[i]][S[i+1]]
end for
currentCost <-- currentCost+Cost[S[m-1]][0] #回到起点0
if currentCost < minCost then #更新全局最优解
minCost <-- currentCost #更新最短距离
bestPath[0] <-- 0 #跟新最短路径
for j <-- 0 to m-1 do
bestPath[j+1] <-- S[j]
end for
bestPath[n] <-- 0 #最后回到起点城市
end if
return #终止递归
end if
for i <-- k to m-1 do
Swap(S[k], S[i]) #交换,确定当前位置k的城市
Solve_TSP(S, k+1, m, Cost) #递归处理下一位置
Swap(S[k], S[i]) #回溯(Backtracking)恢复数组状态
end for4. 实例求解
实例:
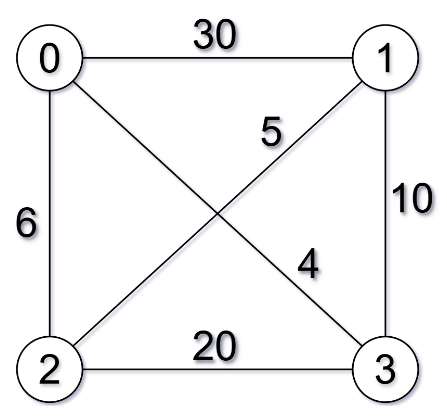
对应Cost邻接矩阵:
Cost=(0306430051065020410200) \large\text{Cost} = \begin{pmatrix} 0 & 30 & 6 & 4 \\ 30 & 0 & 5 & 10 \\ 6 & 5 & 0 & 20 \\ 4 & 10 & 20 & 0 \end{pmatrix} Cost= 0306430051065020410200
固定起点为 城市 0 ,我们需要对剩余城市 {1,2,3}\{1, 2, 3\}{1,2,3} 进行全排列,共有 (4−1)!=6(4-1)! = 6(4−1)!=6 种可能情况:
| 序号 | 城市排列 (S) | 完整回路路径 | 计算过程 | 总距离 |
|---|---|---|---|---|
| 1 | [1, 2, 3] | 0→1→2→3→00 \to 1 \to 2 \to 3 \to 00→1→2→3→0 | 30+5+20+430 + 5 + 20 + 430+5+20+4 | 59 |
| 2 | [1, 3, 2] | 0→1→3→2→00 \to 1 \to 3 \to 2 \to 00→1→3→2→0 | 30+10+20+630 + 10 + 20 + 630+10+20+6 | 66 |
| 3 | [2, 1, 3] | 0→2→1→3→00 \to 2 \to 1 \to 3 \to 00→2→1→3→0 | 6+5+10+46 + 5 + 10 + 46+5+10+4 | 25 (最优) |
| 4 | [2, 3, 1] | 0→2→3→1→00 \to 2 \to 3 \to 1 \to 00→2→3→1→0 | 6+20+10+306 + 20 + 10 + 306+20+10+30 | 66 |
| 5 | [3, 1, 2] | 0→3→1→2→00 \to 3 \to 1 \to 2 \to 00→3→1→2→0 | 4+10+5+64 + 10 + 5 + 64+10+5+6 | 25 (最优) |
| 6 | [3, 2, 1] | 0→3→2→1→00 \to 3 \to 2 \to 1 \to 00→3→2→1→0 | 4+20+5+304 + 20 + 5 + 304+20+5+30 | 59 |
通过穷举发现,最短距离为 25。
对应的最优路径有两条(互为逆向):
- 0→2→1→3→00 \to 2 \to 1 \to 3 \to 00→2→1→3→0
- 0→3→1→2→00 \to 3 \to 1 \to 2 \to 00→3→1→2→0

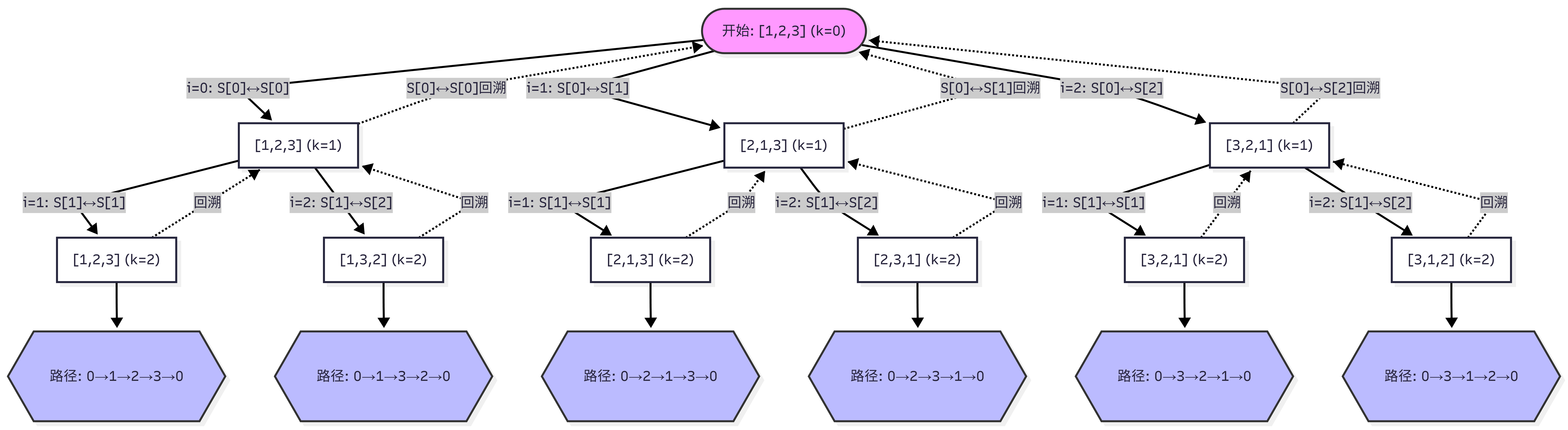
TSP 蛮力法解空间搜索树(以排列3个城市[1,2,3]为例,共生成 3!=6 条路径):
5. 复杂度推导
时间复杂度
1. 递归式定义:
设 T(n)T(n)T(n) 为求解 nnn 个城市 TSP 的时间复杂度:
{T(1)=O(1)T(n)=(n−1)×T(n−1)+O(n) \large\begin{cases} T(1) = O(1) \\ T(n) = (n-1) \times T(n-1) + O(n) \end{cases} ⎩ ⎨ ⎧T(1)=O(1)T(n)=(n−1)×T(n−1)+O(n)
注:选第一个城市有 n−1n-1n−1 种可能;O(n)O(n)O(n) 为最后计算路径距离的开销。
2. 推导过程:
T(n)=(n−1)×T(n−1)+O(n)=(n−1)(n−2)T(n−2)+(n−1)O(n−1)+O(n)=(n−1)!×T(1)+O(n×(n−1)!)=O(n!) \large\begin{align*} T(n) &= (n-1) \times T(n-1) + O(n) \\ &= (n-1)(n-2)T(n-2) + (n-1)O(n-1) + O(n) \\ &= (n-1)! \times T(1) + O(n \times (n-1)!) \\ &= O(n!) \end{align*} T(n)=(n−1)×T(n−1)+O(n)=(n−1)(n−2)T(n−2)+(n−1)O(n−1)+O(n)=(n−1)!×T(1)+O(n×(n−1)!)=O(n!)
固定起点后,n−1n-1n−1 个城市的全排列数为 (n−1)!(n-1)!(n−1)!,每个排列需 O(n)O(n)O(n) 时间计算路径,总复杂度为
O(n×(n−1)!)=O(n!) \large O(n \times (n-1)!) = \mathbf{O(n!)} O(n×(n−1)!)=O(n!)
空间复杂度
由于使用原地交换(Swap)和回溯,空间主要消耗在递归栈上,深度为 O(n)O(n)O(n)。
二、动态规划算法-Held-Karp
1. 求解思路
动态规划(DP)的核心思想是利用 最优子结构 和 重叠子问题 性质,通过"记住"子问题的最优解来大幅提升效率,消除全排列搜索中的冗余计算。
1. 最优子结构
若路径 c₁→...→cₙ₋₁→cₙ 是城市 {c₁,c₂,...,cₙ} 的最短路径,则其子路径 c₁→...→cₙ₋₁ 必然是城市 {c₁,c₂,...,cₙ₋₁} 中 "从 c₁到 cₙ₋₁、经过其他城市各一次" 的最短路径。
2. 重叠子问题
比如路径 c₁→c₂→c₃→c₄→...→cₙ 和 c₁→c₃→c₂→c₄→...→cₙ,虽前半段不同,但都包含相同的子路径 c₄→...→cₙ ------ 这类重复的子问题就是 "重叠" 的。
- 消除冗余:无论以何种顺序访问一组城市,只要已访问的城市集合相同且当前停留城市相同,则从该点出发完成剩余旅程的最优策略是唯一的。
- 状态表示 :通过两个维度锁定一个"状态":
- 已走过的城市集合 SSS:代表当前已经完成了哪些访问任务。
- 当前所在的城市 ccc:代表接下来的旅程从哪里开始。
- 自底向上构建 :从小规模子集(大小为 1)开始,利用已计算的结果逐步推导出规模为 2, 3 直至 n−1n-1n−1 的子集最优路径。
2. 递归式
递归式描述了如何从已知的小规模问题推导出更大规模的问题。
-
基础情况 :对于只包含一个城市 {i}\{i\}{i} 的子集,路径即为从固定起点 0 直达该城市的距离。
-
递推步骤:要计算"经过集合 SSS 且最终停留在城市 ccc"的最短路径:
Dist(S,c)=minj∈S∖{c}{Dist(S∖{c},j)+Cost(j,c)} \large Dist(S, c) = \min_{j \in S \setminus \{c\}} \{Dist(S \setminus \{c\}, j) + Cost(j, c)\} Dist(S,c)=j∈S∖{c}min{Dist(S∖{c},j)+Cost(j,c)}即遍历集合中除 ccc 以外的每一个城市 jjj 作为"上一站",找到能使总距离最小的路径。 -
最终回路:当子集包含除起点外的所有城市后,比较从每一个可能的"最后一站"回到起点的距离总和,取最小值。
3. 算法伪代码
主函数
c
Function TSP_DP(Cost, n):
Dist <-- [] # 存储 (集合, 当前城市) -> 最短距离
parent <-- [] # 存储 (集合, 当前城市) -> 前驱城市
#1.边界条件:初始化大小为1的子集 (从起点0到城市i)
for i <-- 1 to n - 1 do
S <-- {i}
Dist[(S, i)] <-- Cost[0][i]
parent[(S, i)] <-- 0
end for
#2.状态转移:按子集大小从2遍历到n-1
for size <-- 2 to n-1 do # 控制子集的规模
for 每个大小为size且不含起点0的子集S do #组合
for 每个城市c ∈ S do
prevS <-- S-{c}
Dist[(S, c)] <-- 无穷
for 每个前驱城市prevC ∈ prevS do
currentCost <-- Dist[(prevS, prevC)] + Cost[prevC][c]
if currentCost < Dist[(S, c)] then
Dist[(S, c)] <-- currentCost
parent[(S, c)] <-- prevC
end if
end for
end for
end for
end for
#3.闭合回路:计算回到起点0的最短路径
fullS <-- {1, 2, ..., n-1}
minTotalCost <-- 无穷, lastCity <-- -1
for i <-- 1 to n - 1 do
totalCost <-- Dist[(fullS, i)] + Cost[i][0]
if totalCost < minTotalCost then
minTotalCost <-- totalCost, lastCity <-- i
end if
end for
#4.路径回溯
path <-- ReconstructPath(parent, fullS, lastCity)
return minTotalCost, path路径回溯函数
c
Function ReconstructPath(parent, fullS, lastCity):
#1.初始化:从终点开始倒序回溯
path <-- [0] #存储路径城市,先放入起点城市0
currentCity <-- lastCity #前处理的城市,初始为最后访问的城市
currentS <-- fullS #当前处理的集合,初始为包含所有城市的集合
#2.逆向追踪:通过parent表找回每一个前驱
while currentCity ≠ 0 do
path.append(currentCity) #将当前城市存入路径
prevCity <-- parent[(currentS, currentCity)] #获取前驱城市
currentS <-- currentS - {currentCity} #从集合中减去当前城市
currentCity <-- prevCity #移动到前驱城市,准备下一次查询
end while
#3.闭合:加上起点并修正顺序
path.append(0) #加入最终回到的起点0
Reverse(path) #可将[0,n,n-1,...,0]翻转为[0,...,n-1,n,0]
return path4. 实例求解
Cost矩阵(图同上一解法):
Cost=(0306430051065020410200) \large\text{Cost} = \begin{pmatrix} 0 & 30 & 6 & 4 \\ 30 & 0 & 5 & 10 \\ 6 & 5 & 0 & 20 \\ 4 & 10 & 20 & 0 \end{pmatrix} Cost= 0306430051065020410200
第一阶段:子集大小为 1 (Size = 1)
计算从起点 0 到达单个城市 {i}\{i\}{i} 的最短距离。
- Dist[(1,1)]=Cost[0][1]=30;parent[(1,1)]=0Dist[({1}, 1)] = Cost[0][1] = 30;parent[({1}, 1)] = 0Dist[(1,1)]=Cost[0][1]=30;parent[(1,1)]=0
- Dist[(2,2)]=Cost[0][2]=6;parent[(2,2)]=0Dist[({2}, 2)] = Cost[0][2] = 6;parent[({2}, 2)] = 0Dist[(2,2)]=Cost[0][2]=6;parent[(2,2)]=0
- Dist[(3,3)]=Cost[0][3]=4;parent[(3,3)]=0Dist[({3}, 3)] = Cost[0][3] = 4;parent[({3}, 3)] = 0Dist[(3,3)]=Cost[0][3]=4;parent[(3,3)]=0
第二阶段:子集大小为 2 (Size = 2)
基于第一阶段的结果,计算经过两个城市并停在最后一个城市的距离。
1. 子集 S = {1, 2}
-
停在c=1,prevS=2:c = 1, prevS = {2}:c=1,prevS=2:
Dist[(1,2,1)]=Dist[(2,2)]+Cost[2][1]=6+5=11Dist[({1, 2}, 1)] = Dist[({2}, 2)] + Cost[2][1] = 6 + 5 = \mathbf{11}Dist[(1,2,1)]=Dist[(2,2)]+Cost[2][1]=6+5=11;parent[(1,2,1)]=2parent[({1, 2}, 1)] = 2parent[(1,2,1)]=2
-
停在 c = 2, prevS = {1}:
Dist[(1,2,2)]=Dist[(1,1)]+Cost[1][2]=30+5=35Dist[({1, 2}, 2)] = Dist[({1}, 1)] + Cost[1][2] = 30 + 5 = \mathbf{35}Dist[(1,2,2)]=Dist[(1,1)]+Cost[1][2]=30+5=35;parent[(1,2,2)]=1parent[({1, 2}, 2)] = 1parent[(1,2,2)]=1
2. 子集 S = {1, 3}
-
停在 c = 1, prevS = {3}:
Dist[(1,3,1)]=Dist[(3,3)]+Cost[3][1]=4+10=14Dist[({1, 3}, 1)] = Dist[({3}, 3)] + Cost[3][1] = 4 + 10 = \mathbf{14}Dist[(1,3,1)]=Dist[(3,3)]+Cost[3][1]=4+10=14;parent[(1,3,1)]=3parent[({1, 3}, 1)] = 3parent[(1,3,1)]=3
-
停在 c = 3, prevS = {1}:
Dist[(1,3,3)]=Dist[(1,1)]+Cost[1][3]=30+10=40Dist[({1, 3}, 3)] = Dist[({1}, 1)] + Cost[1][3] = 30 + 10 = \mathbf{40}Dist[(1,3,3)]=Dist[(1,1)]+Cost[1][3]=30+10=40;parent[(1,3,3)]=1parent[({1, 3}, 3)] = 1parent[(1,3,3)]=1
3. 子集 S = {2, 3}
-
停在 c=2,prevS=3:c = 2, prevS = {3}:c=2,prevS=3:
Dist[(2,3,2)]=Dist[(3,3)]+Cost[3][2]=4+20=24Dist[({2, 3}, 2)] = Dist[({3}, 3)] + Cost[3][2] = 4 + 20 = \mathbf{24}Dist[(2,3,2)]=Dist[(3,3)]+Cost[3][2]=4+20=24;parent[(2,3,2)]=3parent[({2, 3}, 2)] = 3parent[(2,3,2)]=3
-
停在 c=3,prevS=2:c = 3, prevS = {2}:c=3,prevS=2:
Dist[(2,3,3)]=Dist[(2,2)]+Cost[2][3]=6+20=26Dist[({2, 3}, 3)] = Dist[({2}, 2)] + Cost[2][3] = 6 + 20 = \mathbf{26}Dist[(2,3,3)]=Dist[(2,2)]+Cost[2][3]=6+20=26;parent[(2,3,3)]=2parent[({2, 3}, 3)] = 2parent[(2,3,3)]=2
第三阶段:子集大小为 3 (Size = 3)
计算经过所有城市 S={1,2,3}S=\{1, 2, 3\}S={1,2,3} 且停在最后一个城市的情况。
1. 停在城市 1 (c=1,prevS={2,3}c=1, prevS=\{2, 3\}c=1,prevS={2,3})
- 经由 2:Dist[({2,3},2)]+Cost[2][1]=24+5=29Dist[(\{2,3\}, 2)] + Cost[2][1] = 24 + 5 = 29Dist[({2,3},2)]+Cost[2][1]=24+5=29
- 经由 3:Dist[({2,3},3)]+Cost[3][1]=26+10=36Dist[(\{2,3\}, 3)] + Cost[3][1] = 26 + 10 = 36Dist[({2,3},3)]+Cost[3][1]=26+10=36
- 取最小值:Dist[({1,2,3},1)]=29Dist[(\{1, 2, 3\}, 1)] = 29Dist[({1,2,3},1)]=29 ; parent[({1,2,3},1)]=2parent[(\{1, 2, 3\}, 1)] = 2parent[({1,2,3},1)]=2
2. 停在城市 2 (c=2,prevS={1,3}c=2, prevS=\{1, 3\}c=2,prevS={1,3})
- 经由 1:Dist[({1,3},1)]+Cost[1][2]=14+5=19Dist[(\{1,3\}, 1)] + Cost[1][2] = 14 + 5 = 19Dist[({1,3},1)]+Cost[1][2]=14+5=19
- 经由 3:Dist[({1,3},3)]+Cost[3][2]=40+20=60Dist[(\{1,3\}, 3)] + Cost[3][2] = 40 + 20 = 60Dist[({1,3},3)]+Cost[3][2]=40+20=60
- 取最小值:Dist[({1,2,3},2)]=19Dist[(\{1, 2, 3\}, 2)] = 19Dist[({1,2,3},2)]=19 ; parent[({1,2,3},2)]=1parent[(\{1, 2, 3\}, 2)] = 1parent[({1,2,3},2)]=1
3. 停在城市 3 (c=3,prevS={1,2}c=3, prevS=\{1, 2\}c=3,prevS={1,2})
- 经由 1:Dist[({1,2},1)]+Cost[1][3]=11+10=21Dist[(\{1,2\}, 1)] + Cost[1][3] = 11 + 10 = 21Dist[({1,2},1)]+Cost[1][3]=11+10=21
- 经由 2:Dist[({1,2},2)]+Cost[2][3]=35+20=55Dist[(\{1,2\}, 2)] + Cost[2][3] = 35 + 20 = 55Dist[({1,2},2)]+Cost[2][3]=35+20=55
- 取最小值:Dist[({1,2,3},3)]=21Dist[(\{1, 2, 3\}, 3)] = 21Dist[({1,2,3},3)]=21 ; parent[({1,2,3},3)]=1parent[(\{1, 2, 3\}, 3)] = 1parent[({1,2,3},3)]=1
第四阶段:闭合回路 (回到起点 0)
将第三阶段的结果加上回到起点 0 的距离,并确定最终的 lastCity。
- 从 1 回:Dist[({1,2,3},1)]+Cost[1][0]=29+30=59Dist[(\{1, 2, 3\}, 1)] + Cost[1][0] = 29 + 30 = 59Dist[({1,2,3},1)]+Cost[1][0]=29+30=59
- 从 2 回:Dist[({1,2,3},2)]+Cost[2][0]=19+6=25Dist[(\{1, 2, 3\}, 2)] + Cost[2][0] = 19 + 6 = \mathbf{25}Dist[({1,2,3},2)]+Cost[2][0]=19+6=25
- 从 3 回:Dist[({1,2,3},3)]+Cost[3][0]=21+4=25Dist[(\{1, 2, 3\}, 3)] + Cost[3][0] = 21 + 4 = \mathbf{25}Dist[({1,2,3},3)]+Cost[3][0]=21+4=25
最终结果:
- minTotalDist=25minTotalDist = 25minTotalDist=25
- lastCity=2lastCity = 2lastCity=2 (或 3)
路径回溯演示 (基于 lastCity=2lastCity = 2lastCity=2)
利用上面记录的 parent 映射进行回溯:
- 从最后状态出发:当前城市 222,当前集合 {1,2,3}\{1, 2, 3\}{1,2,3}。
- 查表 parent[({1,2,3},2)]parent[(\{1, 2, 3\}, 2)]parent[({1,2,3},2)] 得到 1。
- 进入下一状态:当前城市 111,当前集合变为 {1,3}\{1, 3\}{1,3}。
- 查表 parent[({1,3},1)]parent[(\{1, 3\}, 1)]parent[({1,3},1)] 得到 3。(见第二阶段)
- 进入下一状态:当前城市 333,当前集合变为 {3}\{3\}{3}。
- 查表 parent[({3},3)]parent[(\{3\}, 3)]parent[({3},3)] 得到 0 。(见第一阶段)
最终路径:0 → 3 → 1 → 2 → 0
5. 复杂度推导
时间复杂度
设除去起点外剩余城市数量为 m=n−1m = n-1m=n−1。核心状态转移的求和表达式为:
T(n)=∑k=2m((mk)×k×(k−1)) \large T(n) = \sum_{k=2}^{m} \left( \binom{m}{k} \times k \times (k-1) \right) T(n)=k=2∑m((km)×k×(k−1))
推导部分:
由于
k(k−1)(mk)=m(m−1)(m−2k−2)① \large k(k-1) \binom{m}{k} = m(m-1) \binom{m-2}{k-2} \quad \text{①} k(k−1)(km)=m(m−1)(k−2m−2)①
则整个求和式等于:
m(m−1)∑k=2m−2(m−2k−2)=m(m−1)2m−2② \large m(m-1) \sum_{k=2}^{m-2} \binom{m-2}{k-2} = m(m-1) 2^{m-2} \quad \text{②} m(m−1)k=2∑m−2(k−2m−2)=m(m−1)2m−2②
代入 m=n−1m = n-1m=n−1:
T(n)=(n−1)(n−2)2n−3 \large T(n) = (n-1)(n-2) 2^{n-3} T(n)=(n−1)(n−2)2n−3
最终:
T(n)=(n−1)(n−2)2n−3=O(n22n) \large T(n) = (n-1)(n-2)2^{n-3} = \mathbf{O(n^2 2^n)} T(n)=(n−1)(n−2)2n−3=O(n22n)
注:
① 式的推导:
从左边出发,利用组合数的定义展开:
k(k−1)(mk)=k(k−1)⋅m!k!(m−k)! k(k - 1) \binom{m}{k} = k(k - 1) \cdot \frac{m!}{k!(m - k)!} k(k−1)(km)=k(k−1)⋅k!(m−k)!m!
注意到 k! = k(k - 1)(k - 2)!,因此
k(k−1)⋅m!k(k−1)(k−2)!(m−k)!=m!(k−2)!(m−k)! k(k - 1) \cdot \frac{m!}{k(k - 1)(k - 2)! (m - k)!} = \frac{m!}{(k - 2)! (m - k)!} k(k−1)⋅k(k−1)(k−2)!(m−k)!m!=(k−2)!(m−k)!m!
再看右边:
m(m−1)(m−2k−2)=m(m−1)⋅(m−2)!(k−2)! [(m−2)−(k−2)]!=m(m−1)⋅(m−2)!(k−2)!(m−k)! m(m - 1) \binom{m - 2}{k - 2} = m(m - 1) \cdot \frac{(m - 2)!}{(k - 2)! \, [(m - 2) - (k - 2)]!} = m(m - 1) \cdot \frac{(m - 2)!}{(k - 2)! (m - k)!} m(m−1)(k−2m−2)=m(m−1)⋅(k−2)![(m−2)−(k−2)]!(m−2)!=m(m−1)⋅(k−2)!(m−k)!(m−2)!
由于 m(m−1)(m−2)!=m!m(m - 1)(m - 2)! = m!m(m−1)(m−2)!=m!,故
m(m−1)(m−2k−2)=m!(k−2)!(m−k)! m(m - 1) \binom{m - 2}{k - 2} = \frac{m!}{(k - 2)! (m - k)!} m(m−1)(k−2m−2)=(k−2)!(m−k)!m!
因此,
k(k−1)(mk)=m!(k−2)!(m−k)!=m(m−1)(m−2k−2) k(k - 1) \binom{m}{k} = \frac{m!}{(k - 2)! (m - k)!} = m(m - 1) \binom{m - 2}{k - 2} k(k−1)(km)=(k−2)!(m−k)!m!=m(m−1)(k−2m−2)
即 ① 式得证。
② 式的推导:
由二项式定理
∑k=0n(nk)xk=(1+x)n,令 x=1,得∑k=0n(nk)=2n \sum_{k=0}^{n} \binom{n}{k} x^k = (1 + x)^n, \quad \text{令 \(x = 1\),得}\sum_{k=0}^{n} \binom{n}{k} = 2^n k=0∑n(kn)xk=(1+x)n,令 x=1,得k=0∑n(kn)=2n
其中令 (j = k - 2)。此即 ② 式。
∑k=2m(m−2k−2)=∑j=0m−2(m−2j)=2 m−2 \sum_{k=2}^{m} \binom{m-2}{k-2} = \sum_{j=0}^{m-2} \binom{m-2}{j} = 2^{\,m-2} k=2∑m(k−2m−2)=j=0∑m−2(jm−2)=2m−2
空间复杂度
由于需要存储所有状态 (S,c)(S, c)(S,c),子集 SSS 有 2n−12^{n-1}2n−1 种,当前城市 ccc 有 n−1n-1n−1 种,空间复杂度为 O(n2n)O(n 2^n)O(n2n)。、
TSP算法分类、演进

Python代码实现
蛮力法:
python
import numpy as np
import itertools
def solve_tsp_brute_force(dist_matrix, current_min, verbose=False, path_history=None):
"""
递归核心:基于交换的全排列生成
:param s: 当前路径数组 (list)
:param k: 当前正在确定的位置索引
:param n: 城市总数
:param dist_matrix: 距离矩阵
:param current_min: 存储最优结果的列表 [min_dist, best_path]
"""
"""使用itertools.permutations生成所有可能的路径并计算最短距离
:param dist_matrix: 距离矩阵
:param current_min: 存储最优结果的列表 [min_dist, best_path]
:param verbose: 是否输出详细计算过程
:param path_history: 存储所有检查过的路径
"""
n = len(dist_matrix)
cities = list(range(1, n)) # 不包含起点0的城市列表
# 生成所有可能的排列(全排列)
for perm in itertools.permutations(cities):
# 将排列转换为列表
route = list(perm)
path = [0] + route + [0] # 完整路径:0 -> 城市1 -> 城市2 -> ... -> 0
# 计算路径总距离
total_dist = 0.0
# 1. 起点到第一个城市的距离
total_dist += dist_matrix[0][route[0]]
# 2. 中间城市之间的距离
for i in range(len(route) - 1):
total_dist += dist_matrix[route[i]][route[i + 1]]
# 3. 最后一个城市回到起点的距离
total_dist += dist_matrix[route[-1]][0]
# 输出详细计算过程
if verbose:
path_str = ' -> '.join(map(str, path))
path_history.append((path_str, total_dist))
print(f"检查路径: {path_str}, 距离: {total_dist}")
# 更新全局最小值
if total_dist < current_min[0]:
current_min[0] = total_dist
current_min[1] = path
if verbose:
print(f"发现更优解! 更新最短距离: {total_dist}, 路径: {path_str}")
def brute_force_tsp(dist_matrix, verbose=False):
"""
主函数入口 - 使用全排列方法
:param dist_matrix: 距离矩阵
:param verbose: 是否输出详细计算过程
:return: (最优路径, 最短距离)
"""
n = len(dist_matrix)
if n <= 1: return [0], 0.0
# 用一个列表来保存可变的最优解 [距离, 路径]
current_min = [float('inf'), []]
# 用于存储所有检查过的路径
path_history = []
if verbose:
print("\nTSP蛮力法求解过程")
print(f"城市数量: {n}")
print(f"距离矩阵:\n{dist_matrix}")
print("\n开始生成并检查所有可能的路径...")
# 使用itertools.permutations生成所有可能的路径
solve_tsp_brute_force(dist_matrix, current_min, verbose, path_history)
if verbose:
print(f"\n共检查了 {len(path_history)} 条可能的路径")
print("求解过程结束\n")
return current_min[1], current_min[0]
#============测试=================
if __name__ == "__main__":
# 定义4城市距离矩阵
distance_matrix = np.array([
[0, 30, 6, 4],
[30, 0, 5, 10],
[6, 5, 0, 20],
[4, 10, 20, 0]
])
# 直接运行TSP蛮力法测试
print("执行测试: 4城市TSP问题")
path, dist = brute_force_tsp(distance_matrix, verbose=True)
print("\nTSP的蛮力法求解结果:")
print(f"最短路径: {path}")
print(f"最短距离: {dist}")Held-Karp动态规划算法
python
import itertools
import numpy as np
def tsp_dp_with_path(dist_matrix, verbose=False):
n = len(dist_matrix)
if n <= 1: return [0], 0.0
if verbose:
print("\nTSP动态规划法求解过程")
print(f"城市数量: {n}")
print(f"距离矩阵:\n{np.array(dist_matrix)}")
print("\n开始DP求解...")
# dp: {(集合, 当前城市): 最短距离}
dp = {}
# parent: {(集合, 当前城市): 最优前驱城市}
parent = {}
# 1. 边界条件:初始化大小为 1 的子集 (0 -> c)
if verbose:
print("\n步骤1: 初始化从起点0到各个城市的直接距离")
for c in range(1, n):
s = frozenset([c])
dp[(s, c)] = dist_matrix[0][c]
parent[(s, c)] = 0 # 前驱是起点 0
if verbose:
print(f" 设置 dp[({{{c}}}, {c})] = {dist_matrix[0][c]} (从城市0到城市{c}的距离)")
# 2. 状态转移:按集合大小从 2 遍历到 n-1
for size in range(2, n):
if verbose:
print(f"\n步骤2.{size-1}: 处理大小为 {size} 的子集")
for combo in itertools.combinations(range(1, n), size):
current_set = frozenset(combo)
if verbose:
set_str = '{' + ', '.join(map(str, current_set)) + '}'
print(f" 处理子集 {set_str}:")
for c in current_set:
prev_set = current_set - {c}
best_dist = float('inf')
best_prev = -1
# 寻找使路径最短的前驱城市 prev_c
for prev_c in prev_set:
dist = dp[(prev_set, prev_c)] + dist_matrix[prev_c][c]
if verbose:
prev_set_str = '{' + ', '.join(map(str, prev_set)) + '}'
print(f" 尝试: 从子集 {prev_set_str} 中的城市 {prev_c} 到城市 {c}")
print(f" 距离 = dp[({prev_set_str}, {prev_c})] + dist[{prev_c}][{c}] = {dp[(prev_set, prev_c)]} + {dist_matrix[prev_c][c]} = {dist}")
if dist < best_dist:
best_dist = dist
best_prev = prev_c
if verbose:
print(f" 更新最优解: 前驱城市 = {best_prev}, 距离 = {best_dist}")
dp[(current_set, c)] = best_dist
parent[(current_set, c)] = best_prev
if verbose:
current_set_str = '{' + ', '.join(map(str, current_set)) + '}'
print(f" 设置 dp[({current_set_str}, {c})] = {best_dist}, 前驱城市 = {best_prev}")
# 3. 最后回到起点:计算包含所有城市并回到 0 的最短回路
full_set = frozenset(range(1, n))
min_total_dist = float('inf')
last_city = -1
if verbose:
print("\n步骤3: 计算从各个城市回到起点的最短回路")
full_set_str = '{' + ', '.join(map(str, full_set)) + '}'
for c in range(1, n):
total_dist = dp[(full_set, c)] + dist_matrix[c][0]
if verbose:
print(f" 尝试从城市 {c} 回到起点 0:")
print(f" 总距离 = dp[({full_set_str}, {c})] + dist[{c}][0] = {dp[(full_set, c)]} + {dist_matrix[c][0]} = {total_dist}")
if total_dist < min_total_dist:
min_total_dist = total_dist
last_city = c
if verbose:
print(f" 更新最优解: 最后一个城市 = {last_city}, 总距离 = {min_total_dist}")
# 4. 路径回溯 (Path Reconstruction)
if verbose:
print("\n步骤4: 路径回溯,重建最优路径")
path = [0] # 这里的 0 是回到起点的那个 0
curr_c = last_city
curr_set = full_set
if verbose:
print(f" 从最后一个城市 {curr_c} 开始回溯")
while curr_c != 0:
path.append(curr_c)
prev_c = parent[(curr_set, curr_c)]
if verbose:
curr_set_str = '{' + ', '.join(map(str, curr_set)) + '}'
print(f" 当前城市 {curr_c}, 前驱城市 = parent[({curr_set_str}, {curr_c})] = {prev_c}")
curr_set = curr_set - {curr_c}
curr_c = prev_c
path.append(0) # 起点 0
path.reverse() # 反转得到从起点出发的顺序
if verbose:
print(f"\n最终路径: {path}")
print(f"最短距离: {min_total_dist}")
return path, min_total_dist
#============测试=================
if __name__ == "__main__":
# 4城市距离矩阵
distance_matrix = [
[0, 30, 6, 4],
[30, 0, 5, 10],
[6, 5, 0, 20],
[4, 10, 20, 0]
]
# 直接执行测试
print("执行测试: 4城市TSP问题")
best_path, min_dist = tsp_dp_with_path(distance_matrix, verbose=True)
print("\nTSP的DP法求解结果:")
print(f"最短路径: {best_path}")
print(f"最短距离: {min_dist}")