计算机图形学：【Games101】学习笔记05——着色（插值、高级纹理映射）与几何（基本表示方法）

计算机图形学：【Games101】学习笔记05------着色（插值、高级纹理映射）与几何（基本表示方法）

• 前言
• 一、着色（插值、高级纹理映射）
• • [1.1 重心坐标（Barycentric Coordinates）](#1.1 重心坐标（Barycentric Coordinates）)
  • • [1.1.1 三角形间的插值（Interpolation Across Triangles）](#1.1.1 三角形间的插值（Interpolation Across Triangles）)
    • [1.1.2 重心坐标（Barycentric Coordinates）](#1.1.2 重心坐标（Barycentric Coordinates）)
  • [1.2 应用纹理（Applying Textures）](#1.2 应用纹理（Applying Textures）)
  • • [1.2.1 简单纹理映射：漫反射颜色（Simple Texture Mapping: Diffuse Color）](#1.2.1 简单纹理映射：漫反射颜色（Simple Texture Mapping: Diffuse Color）)
  • [1.3 纹理查询（Texture Queries）](#1.3 纹理查询（Texture Queries）)
  • • [1.3.1 纹理放大（Texture Magnification）](#1.3.1 纹理放大（Texture Magnification）)
    • [1.3.2 纹理放大（复杂案例）（Texture Magnification (hard case)）](#1.3.2 纹理放大（复杂案例）（Texture Magnification (hard case)）)
  • [1.4 纹理映射（Mipmap）](#1.4 纹理映射（Mipmap）)
  • [1.5 各向异性过滤（Anisotropic Filtering）](#1.5 各向异性过滤（Anisotropic Filtering）)
  • [1.6 纹理的应用（Applications of Textures）](#1.6 纹理的应用（Applications of Textures）)
  • • [1.6.1 环境光照（Environment Lighting）](#1.6.1 环境光照（Environment Lighting）)
    • [1.6.2 纹理可以影响着色 （Textures can affect shading! ）](#1.6.2 纹理可以影响着色 （Textures can affect shading! ）)
• 二、几何（基本表示方法）
• • [2.1 几何示例（Examples of Geometry）](#2.1 几何示例（Examples of Geometry）)
  • [2.2 几何的多种表示形式（Many Ways to Represent Geometry）](#2.2 几何的多种表示形式（Many Ways to Represent Geometry）)
  • • [2.2.1 隐式表示（Implicit Representations）](#2.2.1 隐式表示（Implicit Representations）)
    • [2.2.2 显式表示（Explicit Representations）](#2.2.2 显式表示（Explicit Representations）)
    • [2.2.3 计算机图形学中的更多隐式表示（More Implicit Representations in Computer Graphics）](#2.2.3 计算机图形学中的更多隐式表示（More Implicit Representations in Computer Graphics）)
• 三、疑难点整理总结
• 写在最后

前言

• 🎮 GAMES101 是国内相当有名的图形学公开课。项目相关资源在：https://sites.cs.ucsb.edu/~lingqi/teaching/games101.html。
• 本 📒笔记为 🖊️笔者在自学过程中整理的 🇨🇳中文版笔记，供各位 📖读者阅读 😼～
• 计算机图形学中， visibility 处理与着色是实现真实渲染的核心环节。GAMES101 第 7 讲围绕 Z 缓冲算法、着色模型及图形管线展开，清晰拆解了从物体遮挡判断到表面光影呈现的关键技术，本文将梳理核心知识点与实践要点。

一、着色（插值、高级纹理映射）

1.1 重心坐标（Barycentric Coordinates）

1.1.1 三角形间的插值（Interpolation Across Triangles）

为什么需要插值？

在三角形顶点指定属性值，需在三角形内部获得平滑变化的属性值。

插值目标：

纹理坐标、颜色、法向量、深度、材质属性等。

如何插值：

利用重心坐标。

1.1.2 重心坐标（Barycentric Coordinates）

1️⃣ 定义

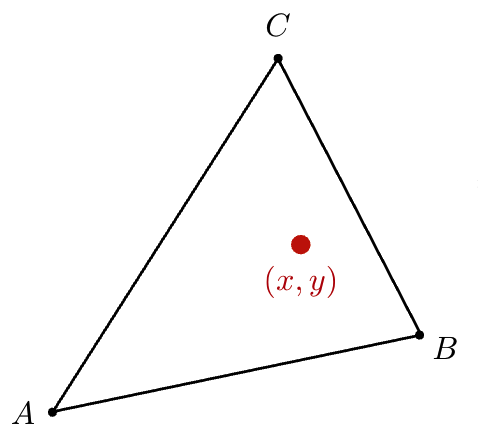
重心坐标是三角形专属的坐标系，对于三角形内任意一点 ( x , y ) (x, y) (x,y)，可表示为三个顶点的线性组合： ( x , y ) = α A + β B + γ C (x, y) = \alpha A + \beta B + \gamma C (x,y)=αA+βB+γC

其中满足约束： α + β + γ = 1 \alpha + \beta + \gamma = 1 α+β+γ=1。

• 点在三角形内部的充要条件： α ≥ 0 \alpha \geq 0 α≥0、 β ≥ 0 \beta \geq 0 β≥0、 γ ≥ 0 \gamma \geq 0 γ≥0。

• 点在三角形边上：某一个坐标为 0。

• 点在三角形顶点：两个坐标为 0。

2️⃣ 特殊点的重心坐标

• 顶点 A 的坐标： ( α , β , γ ) = ( 1 , 0 , 0 ) (\alpha, \beta, \gamma) = (1, 0, 0) (α,β,γ)=(1,0,0)（代入公式得 ( x , y ) = A (x,y)=A (x,y)=A ）；
• 三角形重心（形心）坐标： ( α , β , γ ) = ( 1 3 , 1 3 , 1 3 ) (\alpha, \beta, \gamma) = (\frac{1}{3}, \frac{1}{3}, \frac{1}{3}) (α,β,γ)=(31,31,31)（三点加权平均）。

3️⃣ 几何意义：面积比例

重心坐标的三个分量对应 "子三角形面积" 与 "原三角形总面积" 的比值： α = A A A A + A B + A C , β = A B A A + A B + A C , γ = A C A A + A B + A C \alpha = \frac{A_A}{A_A + A_B + A_C}, \quad \beta = \frac{A_B}{A_A + A_B + A_C}, \quad \gamma = \frac{A_C}{A_A + A_B + A_C} α=AA+AB+ACAA,β=AA+AB+ACAB,γ=AA+AB+ACAC

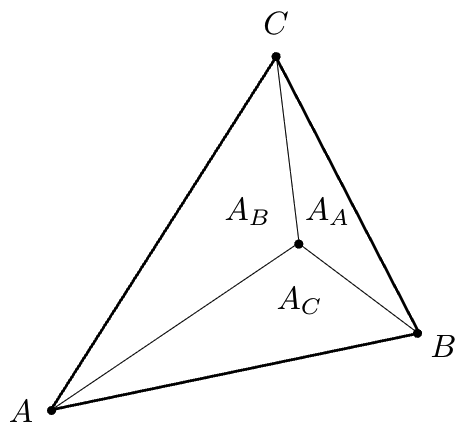
其中：

• A A A_A AA：点 ( x , y ) (x,y) (x,y) 与顶点 B、C 构成的子三角形面积；
• A B A_B AB：点 ( x , y ) (x,y) (x,y) 与顶点 A、C 构成的子三角形面积；
• A C A_C AC：点 ( x , y ) (x,y) (x,y) 与顶点 A、B 构成的子三角形面积。

4️⃣ 计算公式

已知三角形三个顶点 A ( x A , y A ) A(x_A,y_A) A(xA,yA)、 B ( x B , y B ) B(x_B,y_B) B(xB,yB)、 C ( x C , y C ) C(x_C,y_C) C(xC,yC)，任意点 ( x , y ) (x,y) (x,y) 的重心坐标计算：
α = − ( x − x B ) ( y C − y B ) + ( y − y B ) ( x C − x B ) − ( x A − x B ) ( y C − y B ) + ( y A − y B ) ( x C − x B ) \alpha = \frac{-(x-x_B)(y_C-y_B) + (y-y_B)(x_C-x_B)}{-(x_A-x_B)(y_C-y_B) + (y_A-y_B)(x_C-x_B)} α=−(xA−xB)(yC−yB)+(yA−yB)(xC−xB)−(x−xB)(yC−yB)+(y−yB)(xC−xB) β = − ( x − x C ) ( y A − y C ) + ( y − y C ) ( x A − x C ) − ( x B − x C ) ( y A − y C ) + ( y B − y C ) ( x A − x C ) \beta = \frac{-(x-x_C)(y_A-y_C) + (y-y_C)(x_A-x_C)}{-(x_B-x_C)(y_A-y_C) + (y_B-y_C)(x_A-x_C)} β=−(xB−xC)(yA−yC)+(yB−yC)(xA−xC)−(x−xC)(yA−yC)+(y−yC)(xA−xC) γ = 1 − α − β \gamma = 1 - \alpha - \beta γ=1−α−β

5️⃣ 重心坐标的应用：线性插值

通过重心坐标可插值顶点的任意属性（记顶点属性为 V A , V B , V C V_A, V_B, V_C VA,VB,VC），插值公式： V = α V A + β V B + γ V C V = \alpha V_A + \beta V_B + \gamma V_C V=αVA+βVB+γVC

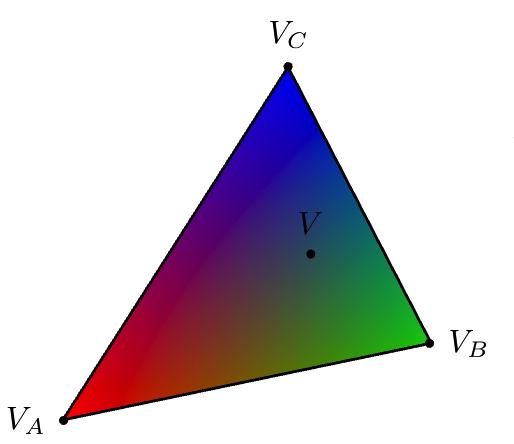
• 可插值属性：位置、纹理坐标、颜色、法向量、深度、材质属性等；
• 注意事项：重心坐标在投影变换下并不具有不变性（投影后插值结果可能失真）；

1.2 应用纹理（Applying Textures）

1.2.1 简单纹理映射：漫反射颜色（Simple Texture Mapping: Diffuse Color）

核心逻辑：将纹理的漫反射反照率 K d K_d Kd（对应 Blinn-Phong 模型）映射到三角形表面，步骤如下：

• 对每个栅格化后的屏幕采样点 ( x , y ) (x,y) (x,y)，通过重心坐标计算对应的纹理坐标 ( u , v ) (u,v) (u,v)；
• 根据 ( u , v ) (u,v) (u,v) 采样纹理颜色： t e x c o l o r = t e x t u r e . s a m p l e ( u , v ) texcolor = texture.sample(u,v) texcolor=texture.sample(u,v)；
• 将采样点颜色设置为纹理颜色 t e x c o l o r texcolor texcolor。

注：通常以像素中心作为采样基准点

1.3 纹理查询（Texture Queries）

1.3.1 纹理放大（Texture Magnification）

1️⃣ 如果纹理太小怎么办？(What if the texture is too small)

问题本质：单个屏幕像素对应纹理中的不足 1 个纹素（texel），需插值补充（纹理尺寸 < 屏幕显示尺寸）。

三种常用的纹理放大插值方法包括：最近邻（Nearest）、双线性（Bilinear）、 双三次（Bicubic）。

2️⃣ 双线性插值（Bilinear Interpolation）

目标 ：想要在红点处对纹理值 f ( x , y ) f(x,y) f(x,y) 进行采样，黑点表示纹理样本位置。

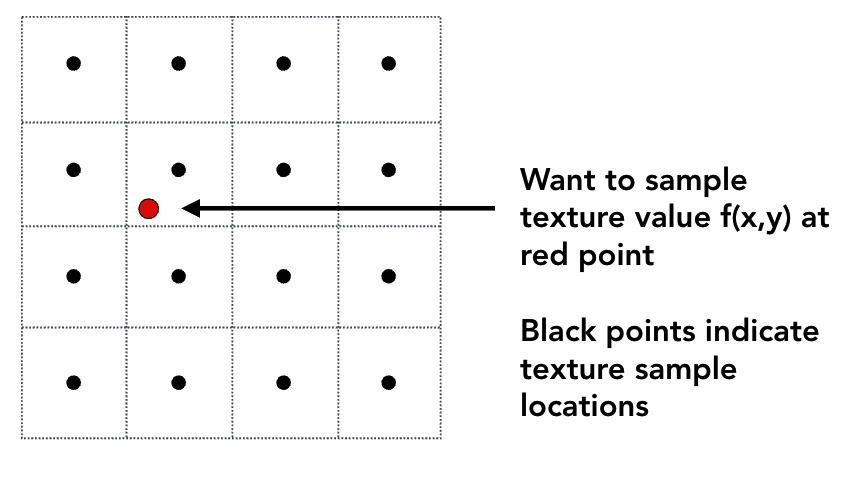
双线性插值步骤：

• 确定采样点 ( u , v ) (u,v) (u,v) 周围的 4 个相邻纹素 u 00 , u 01 , u 10 , u 11 u_{00}, u_{01}, u_{10}, u_{11} u00,u01,u10,u11；
• 计算采样点在 4 个纹素中的分数偏移 ( s , t ) (s,t) (s,t)（范围 [0,1]）；
• 1D 线性插值公式（lerp）： l e r p ( x , v 0 , v 1 ) = v 0 + x ( v 1 − v 0 ) lerp(x, v_0, v_1) = v_0 + x(v_1 - v_0) lerp(x,v0,v1)=v0+x(v1−v0)；
• 水平插值： u 0 = l e r p ( s , u 00 , u 10 ) u_0 = lerp(s, u_{00}, u_{10}) u0=lerp(s,u00,u10)， u 1 = l e r p ( s , u 01 , u 11 ) u_1 = lerp(s, u_{01}, u_{11}) u1=lerp(s,u01,u11)；
• 垂直插值：最终颜色 f ( x , y ) = l e r p ( t , u 0 , u 1 ) f(x,y) = lerp(t, u_0, u_1) f(x,y)=lerp(t,u0,u1)。

步骤一：确定采样点 ( u , v ) (u,v) (u,v) 周围的 4 个相邻纹素 u 00 , u 01 , u 10 , u 11 u_{00}, u_{01}, u_{10}, u_{11} u00,u01,u10,u11。

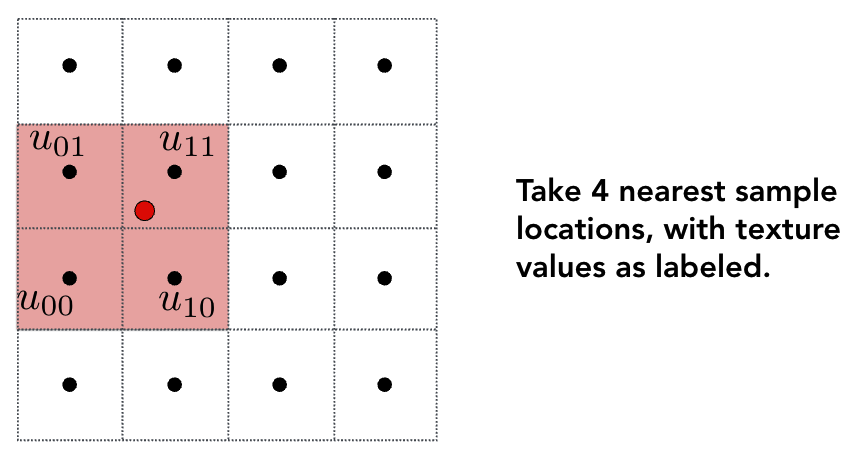
步骤二：计算采样点在 4 个纹素中的分数偏移 ( s , t ) (s,t) (s,t)（范围 [0,1]）。

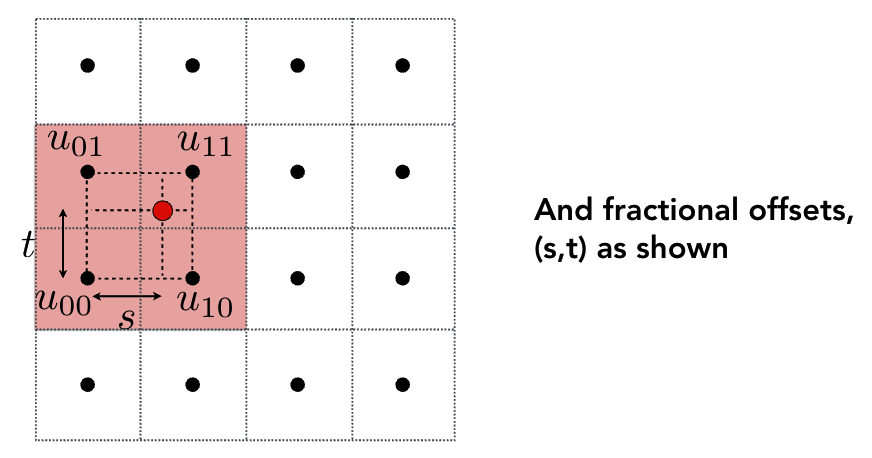
步骤三：1D 线性插值公式（lerp）： l e r p ( x , v 0 , v 1 ) = v 0 + x ( v 1 − v 0 ) lerp(x, v_0, v_1) = v_0 + x(v_1 - v_0) lerp(x,v0,v1)=v0+x(v1−v0)。

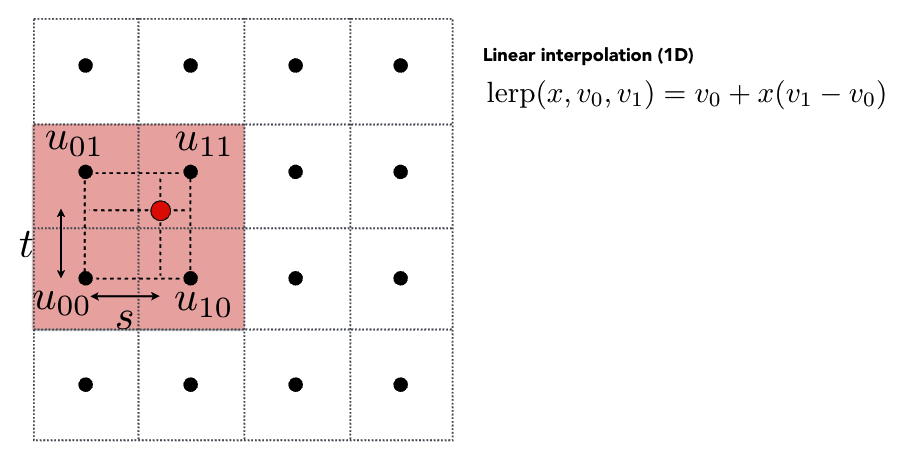
步骤四：水平插值： u 0 = l e r p ( s , u 00 , u 10 ) u_0 = lerp(s, u_{00}, u_{10}) u0=lerp(s,u00,u10)， u 1 = l e r p ( s , u 01 , u 11 ) u_1 = lerp(s, u_{01}, u_{11}) u1=lerp(s,u01,u11)。

步骤五：垂直插值：最终颜色 f ( x , y ) = l e r p ( t , u 0 , u 1 ) f(x,y) = lerp(t, u_0, u_1) f(x,y)=lerp(t,u0,u1)。

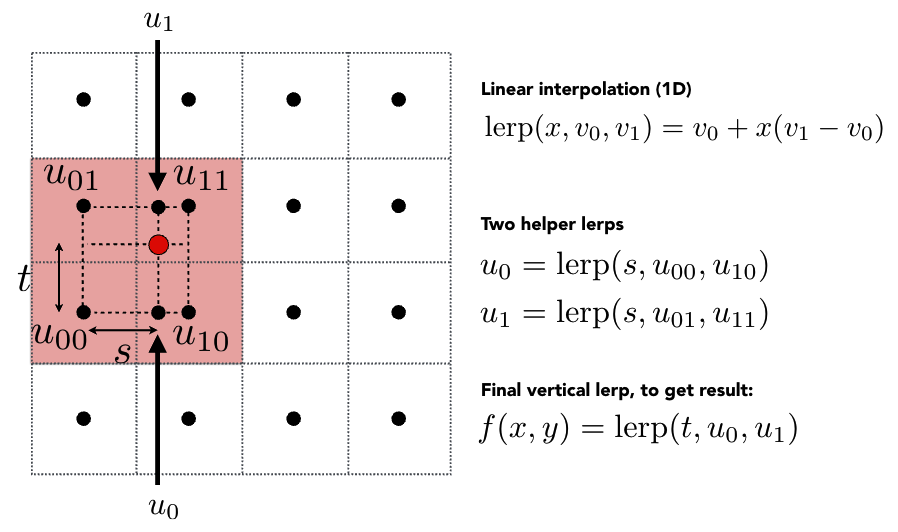
结论：双线性插值通常能以合理的成本产生相当好的结果。

1.3.2 纹理放大（复杂案例）（Texture Magnification (hard case)）

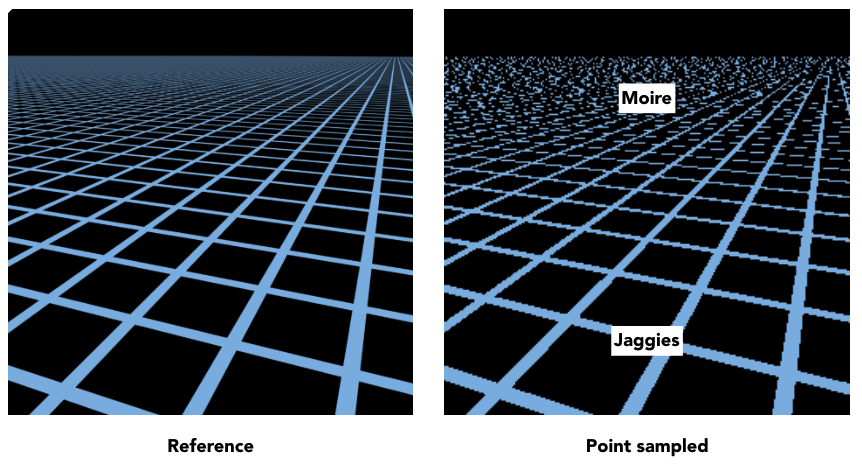
1️⃣ 点采样纹理的问题（Point Sampling Textures --- Problem）

• 摩尔纹（Moire）：周期性纹理重叠产生的干涉条纹。
• 锯齿（Jaggies）：边缘不平滑。

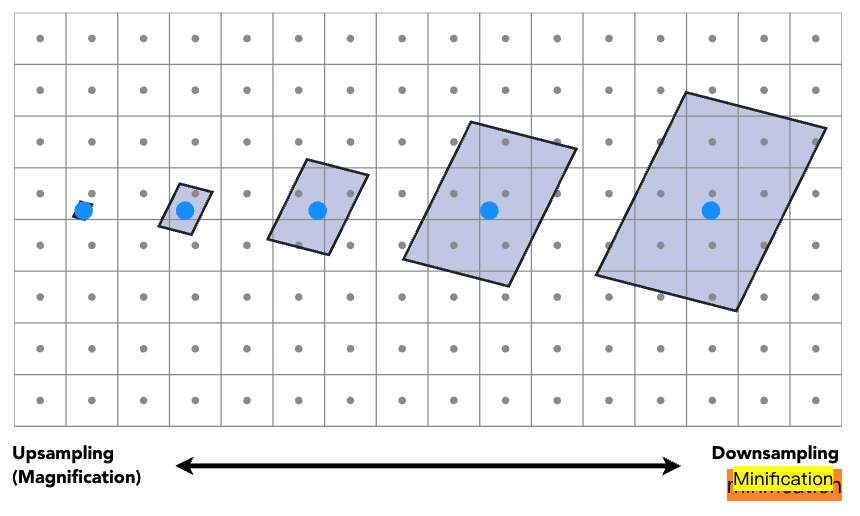
2️⃣ 纹理中的屏幕像素"足迹"（Screen Pixel "Footprint" in Texture）

3️⃣ 解决方案 1：超采样（Supersampling）

超采样能进行抗锯齿处理，但代价极高。

• 当高度缩小时，像素覆盖范围内会包含许多纹理元素；
• 像素中的信号频率过高；
• 需要更高的采样频率；

换一种方式来理解这个问题：如果我们不进行采样会怎样？

只需要获取一个范围内的平均值（Just need to get the average value within a range）！

4️⃣ 不同像素会产生不同的足迹（Different Pixels -> Different-Sized Footprints）

1.4 纹理映射（Mipmap）

更详细的理解：https://blog.csdn.net/qq_42428486/article/details/118856697。

1️⃣ Mipmap 基本思想

核心思想：预计算多分辨率纹理层级，快速获取区域平均值（替代点采样）。名字来源：拉丁语 "multum in parvo"，意为 "小空间容纳多内容"。

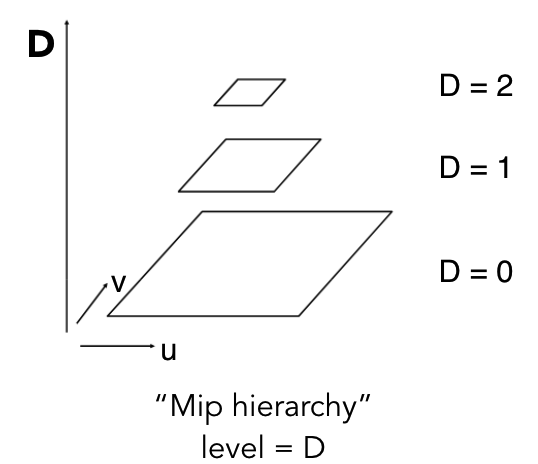
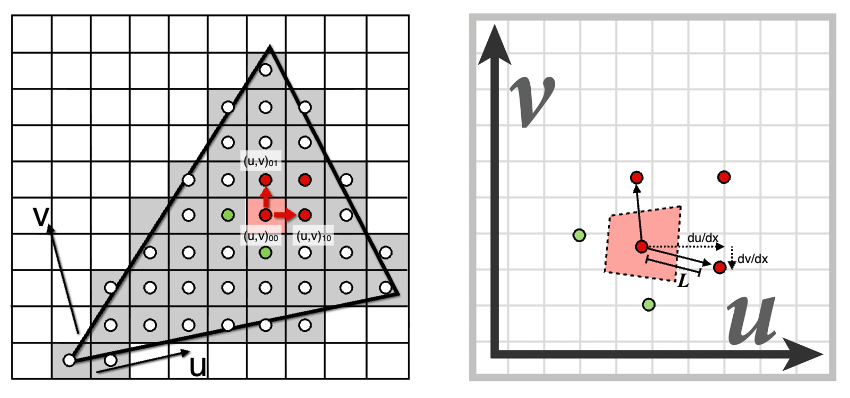
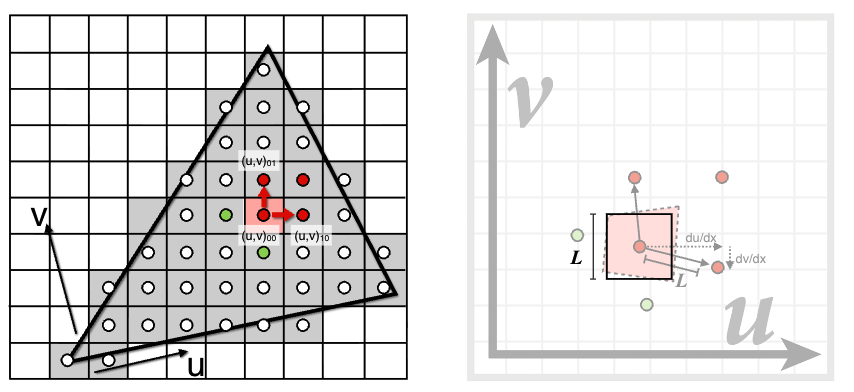
2️⃣ Mipmap 层级计算（Computing Mipmap Level D）

1、利用相邻屏幕样本的纹理坐标估算纹理覆盖范围。

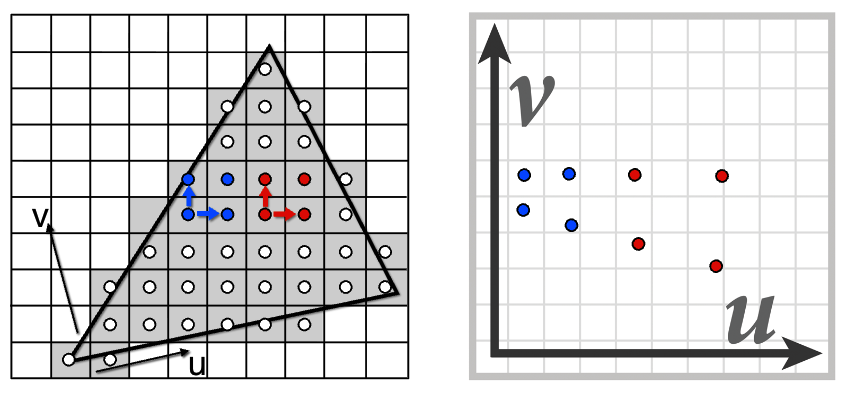
2、计算足迹尺寸 L： L = m a x ( ( d u d x ) 2 + ( d v d x ) 2 , ( d u d y ) 2 + ( d v d y ) 2 ) L = max\left( \sqrt{(\frac{du}{dx})^2 + (\frac{dv}{dx})^2}, \sqrt{(\frac{du}{dy})^2 + (\frac{dv}{dy})^2} \right) L=max((dxdu)2+(dxdv)2 ,(dydu)2+(dydv)2 )。层级 D： D = l o g 2 L D = log_2 L D=log2L（表示需要的纹理缩小层级）。

3️⃣ Mipmap可视化（Visualization of Mipmap Level）

4️⃣ 三线性插值（Trilinear Interpolation）

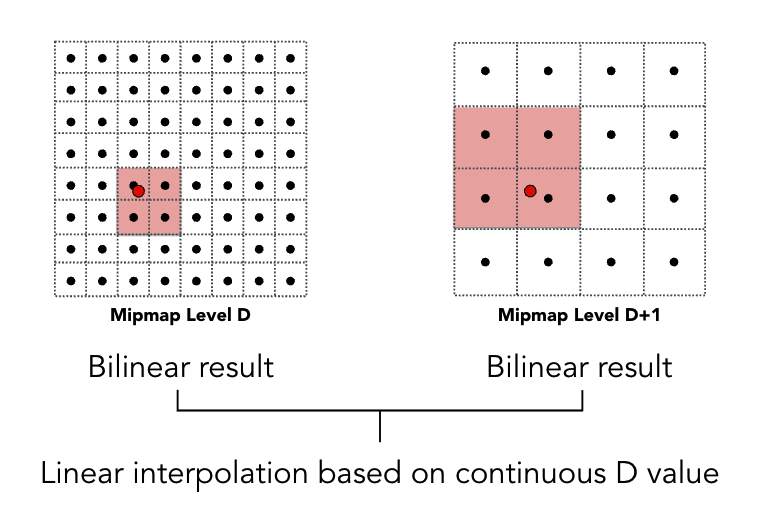
基于三线性过滤的可视化：

5️⃣ Mipmap 局限性

假设像素在纹理中的足迹是方形，但实际可能是不规则形状（如椭圆）。

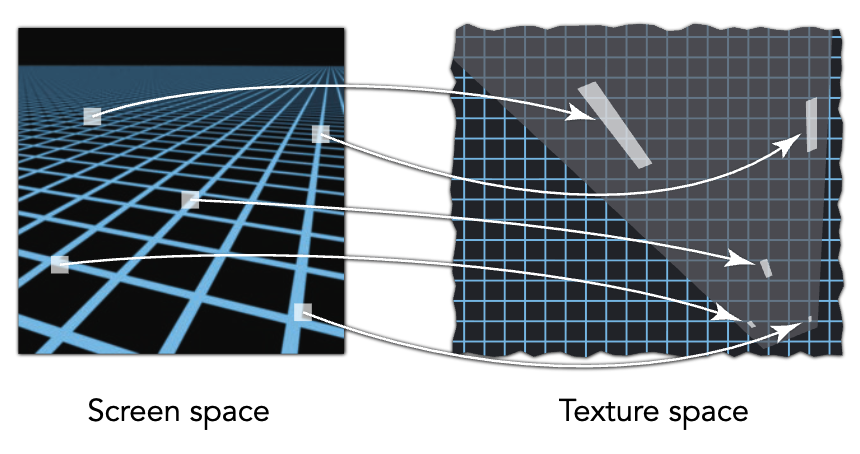
容易产生过度模糊：当足迹为非方形时，方形平均会丢失细节。

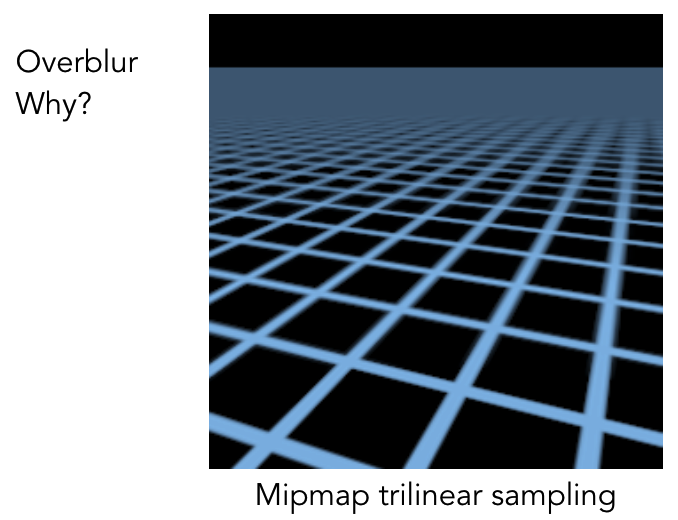
1.5 各向异性过滤（Anisotropic Filtering）

核心目标：解决 Mipmap 无法处理的非方形足迹问题。

关键技术：Ripmaps（波纹纹理）+ 累积面积表（Summed Area Tables）：支持轴对齐矩形足迹查询，但对角线足迹仍有缺陷。

EWA 过滤（Elliptical Weighted Average）：

• 将像素足迹建模为椭圆
• 对椭圆区域进行多个采样点的加权平均
• 结合 Mipmap 层级优化，兼顾效率与细节保留

效果：比 Mipmap 更清晰，能保留非方形足迹区域的纹理细节。

1.6 纹理的应用（Applications of Textures）

现代 GPU 中，纹理 = 内存 + 范围查询（过滤），是将数据带入片段计算的通用方法，具有多种用途。

1.6.1 环境光照（Environment Lighting）

利用环境贴图（Environment Map）模拟环境光源，实现真实感光照渲染（源自 Blinn & Newell 1976 年的研究）。

两种常见环境贴图：

1️⃣ 球形环境贴图（Spherical Environment Map）：存在畸变问题（顶部和底部区域尤为明显），典型例子如埃舍尔的《手持反射球》。

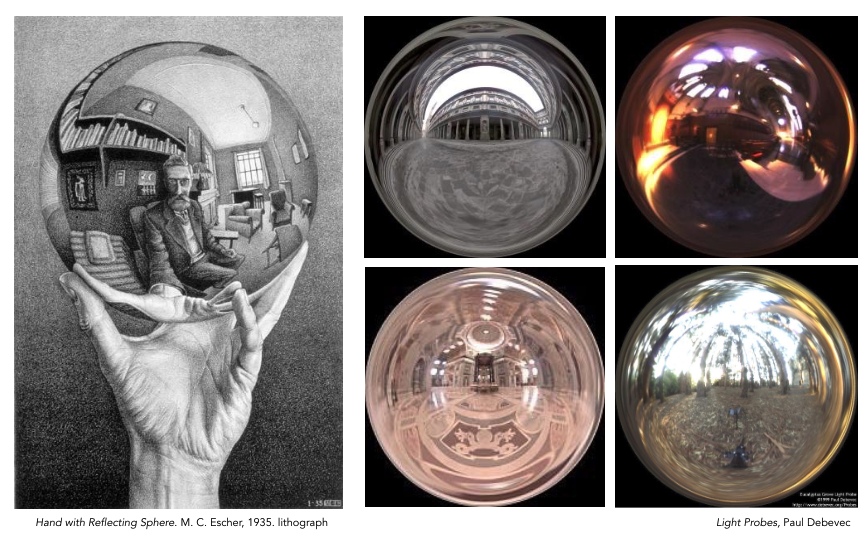
2️⃣ 立方体贴图（Cube Map）：由 6 张正方形纹理组成，将方向向量映射到立方体表面，畸变显著减少；需进行 "方向→面" 的计算（参考 Emil Persson 的研究）。

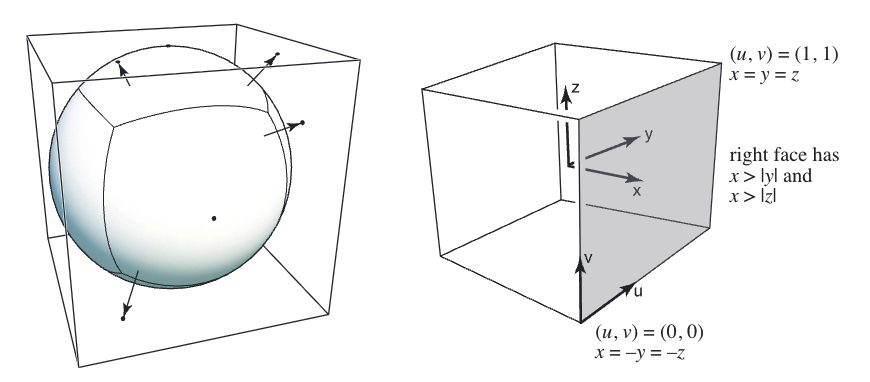
1.6.2 纹理可以影响着色 （Textures can affect shading! ）

通过纹理存储表面细节，无需增加三角形数量。

1️⃣ 凹凸贴图（Bump Mapping）：仅在着色计算中扰动表面法向量，不改变顶点位置（"伪造" 细节几何）。

流程：纹理存储高度信息→通过高度计算法向量→参与着色。

法向量扰动原理

2D 平面场景：原始法向量 n §=(0,1)，导数 dp=c・[h (p+1)-h §]，扰动后法向量 n §=(-dp,1)（归一化）。

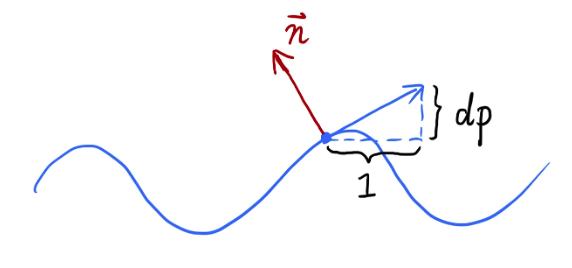
3D 场景：原始法向量 n §=(0,0,1)，导数 dp/du=c1・[h (u+1)-h (u)]、dp/dv=c2・[h (v+1)-h (v)]，扰动后法向量 n=(-dp/du, -dp/dv, 1)（归一化），注意：此计算基于局部坐标系（HW3 的 FAQ 会详细说明）

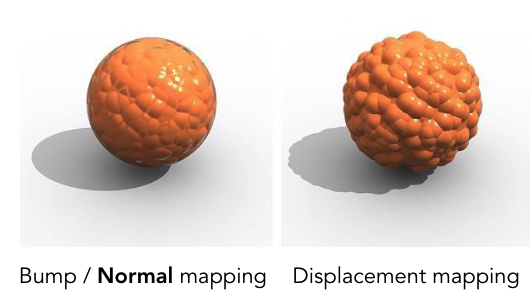
2️⃣ 位移贴图（Displacement Mapping）：与凹凸贴图使用相同纹理，但会实际移动顶点位置，是更高级的细节表现方法。

二、几何（基本表示方法）

涵盖多种场景：汽车模型、COVID-19 模型、自然景观（National Geographic 拍摄案例）等，体现几何在图形学中的广泛应用。

2.1 几何示例（Examples of Geometry）

2.2 几何的多种表示形式（Many Ways to Represent Geometry）

分为两大类，每种方法适用于不同任务 / 几何类型，无绝对 "最优" 选择。

2.2.1 隐式表示（Implicit Representations）

核心定义 ：通过分类点的关系来描述几何，满足特定函数关系的点构成几何表面，通用形式为 f (x,y,z)=0。

优势任务：内部 / 外部判断（直接代入函数计算，f<0 为内部，f>0 为外部）、光线与表面相交计算（后续讲解）、拓扑变化处理（如流体）、简单形状的精确描述（无采样误差）。

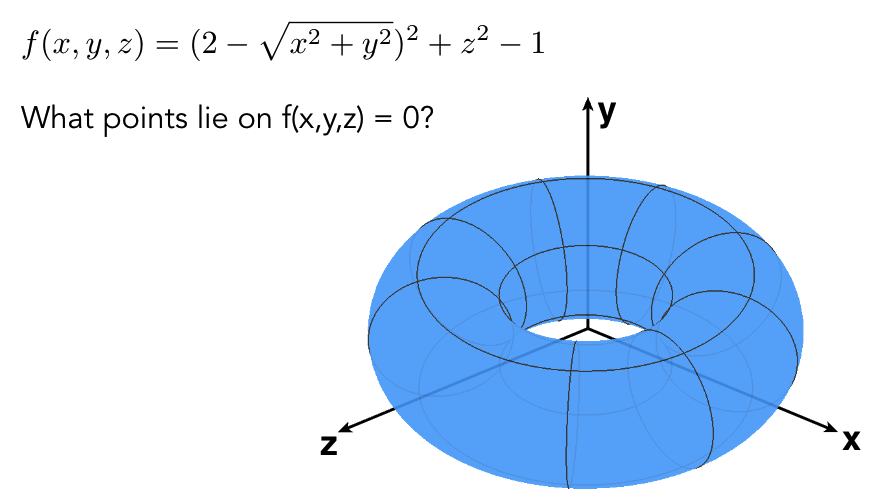
困难任务：采样（难以直接获取表面点）。

隐式表示采样困难举例：

隐式表示内外测试简单举例：

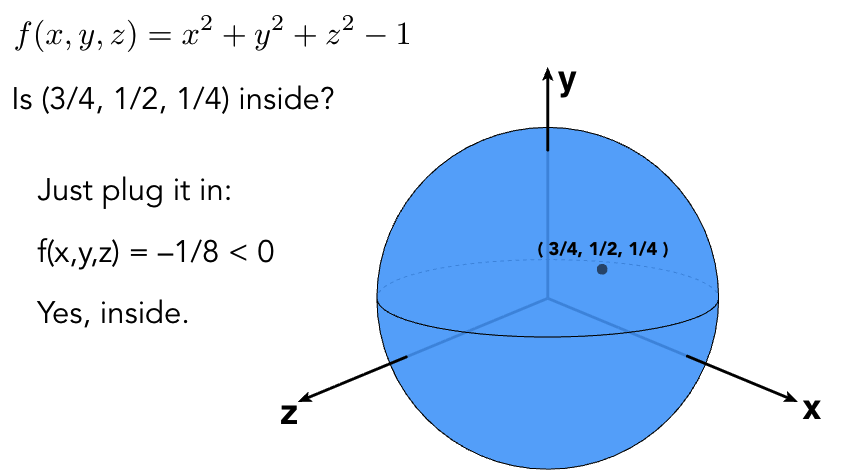
2.2.2 显式表示（Explicit Representations）

核心定义 ：直接给出所有点或通过参数映射生成点，通用形式为 f:ℝ²→ℝ³；(u,v)↦(x,y,z)。

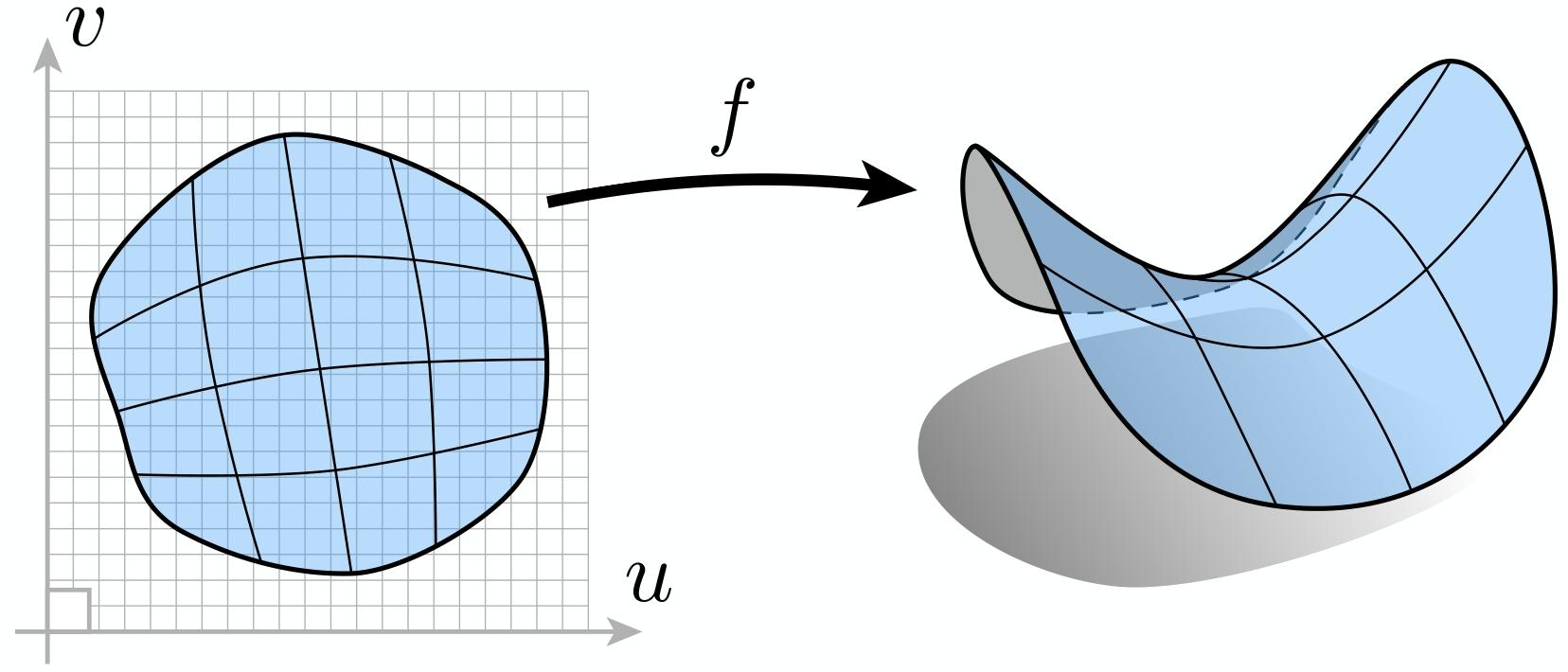
优势任务：采样（直接代入参数 (u,v) 即可获取表面点）。

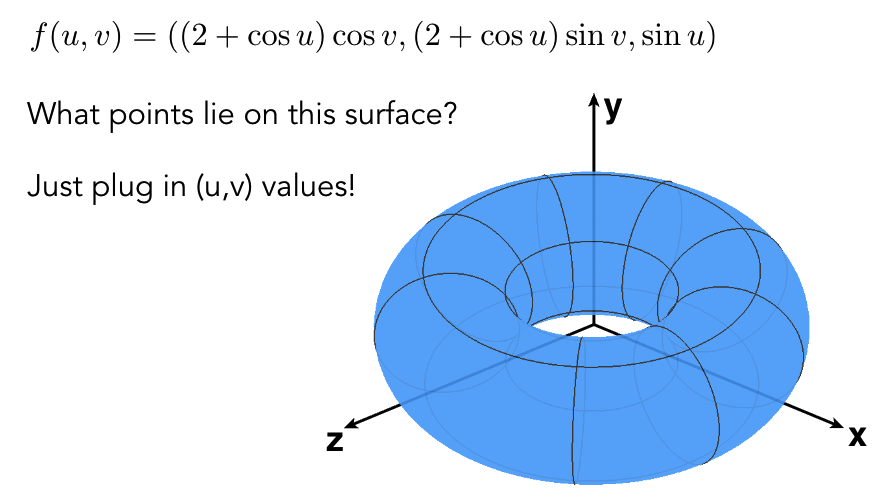
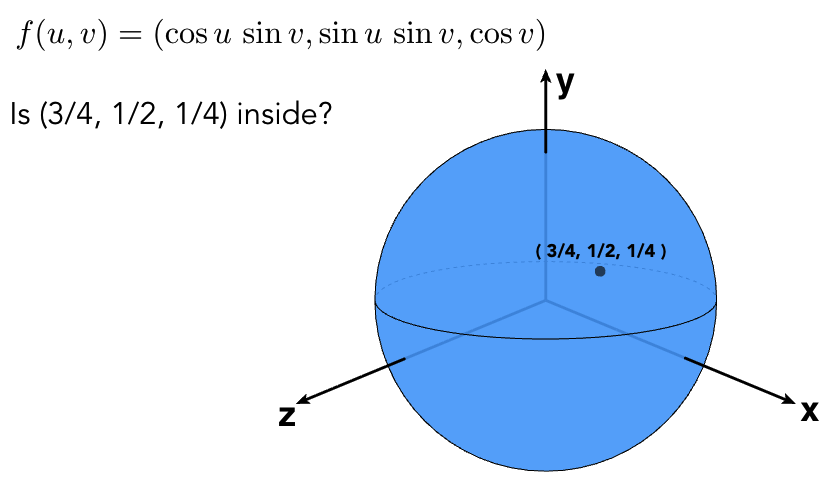
困难任务：内部 / 外部判断（难以通过参数直接判断）

常见类型：点云（Point Cloud）、多边形网格细分（Polygon Mesh Subdivision）、NURBS。

2.2.3 计算机图形学中的更多隐式表示（More Implicit Representations in Computer Graphics）

1️⃣ 代数曲面（Algebraic Surfaces (Implicit)）

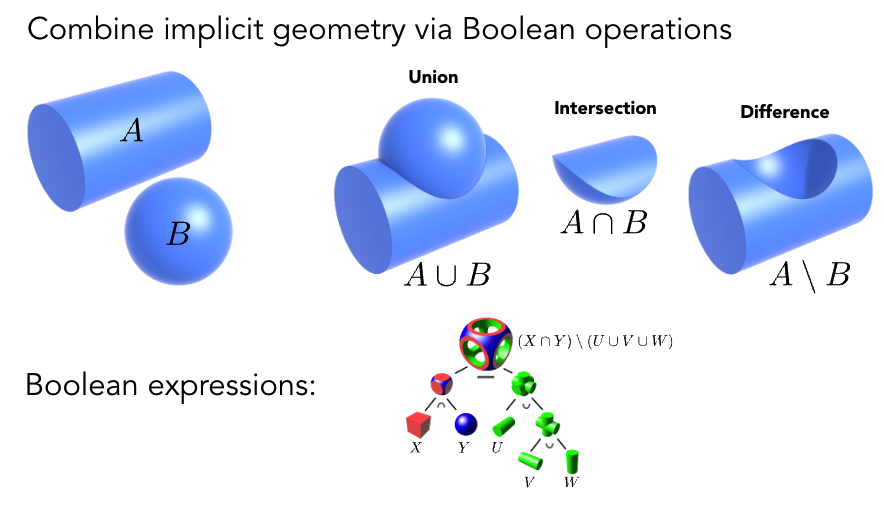
2️⃣ 构造实体几何（Constructive Solid Geometry (Implicit)）

通过布尔运算组合隐式几何：

3️⃣ 距离函数（Distance Functions (Implicit)）

不使用布尔值，而是使用距离函数将曲面逐渐融合在一起：给出从任意位置到物体的最小距离（可以是带符号的距离）。

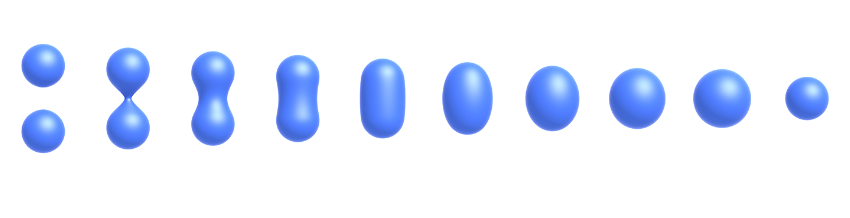
一个示例：混合（线性插值）移动边界。

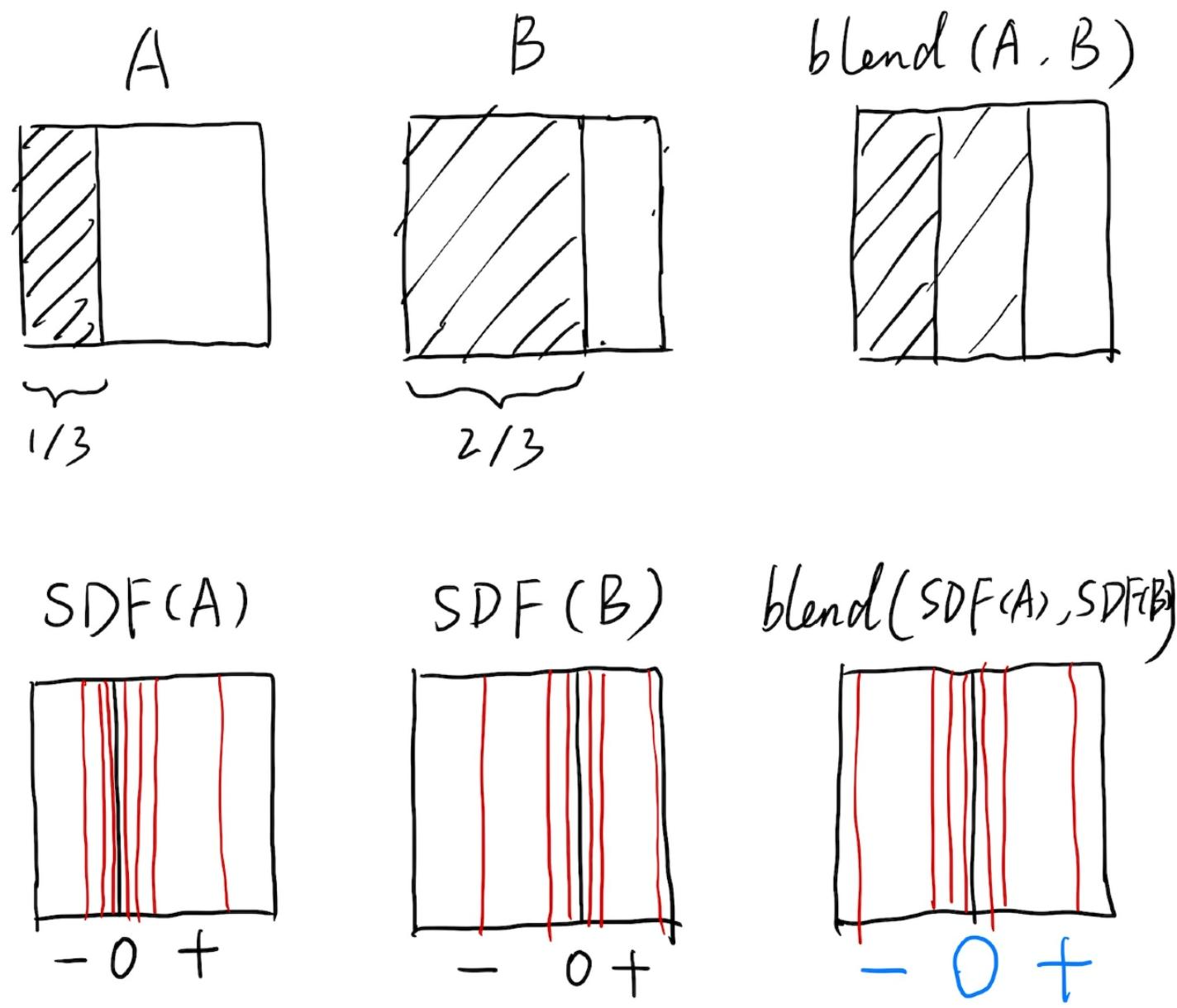
可以混合任意两个距离函数d1、d2：

纯距离函数场景（Scene of Pure Distance Functions）。

4️⃣ 水平集方法（Level Set Methods (Also implicit) ）

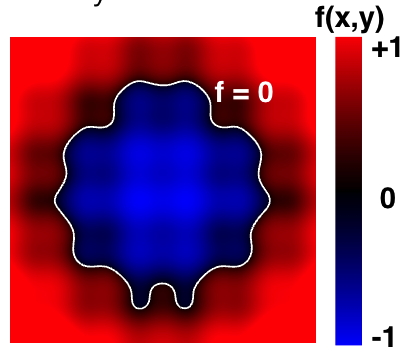
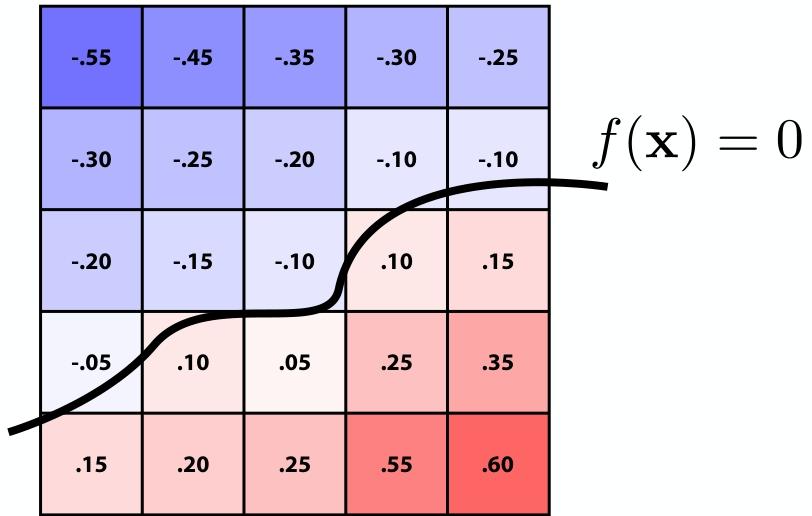
闭式方程难以描述复杂形状。替代方案：存储一个近似函数的值网格。在插值值等于零的地方可以找到曲面，提供对形状更明确的控制（如纹理）。

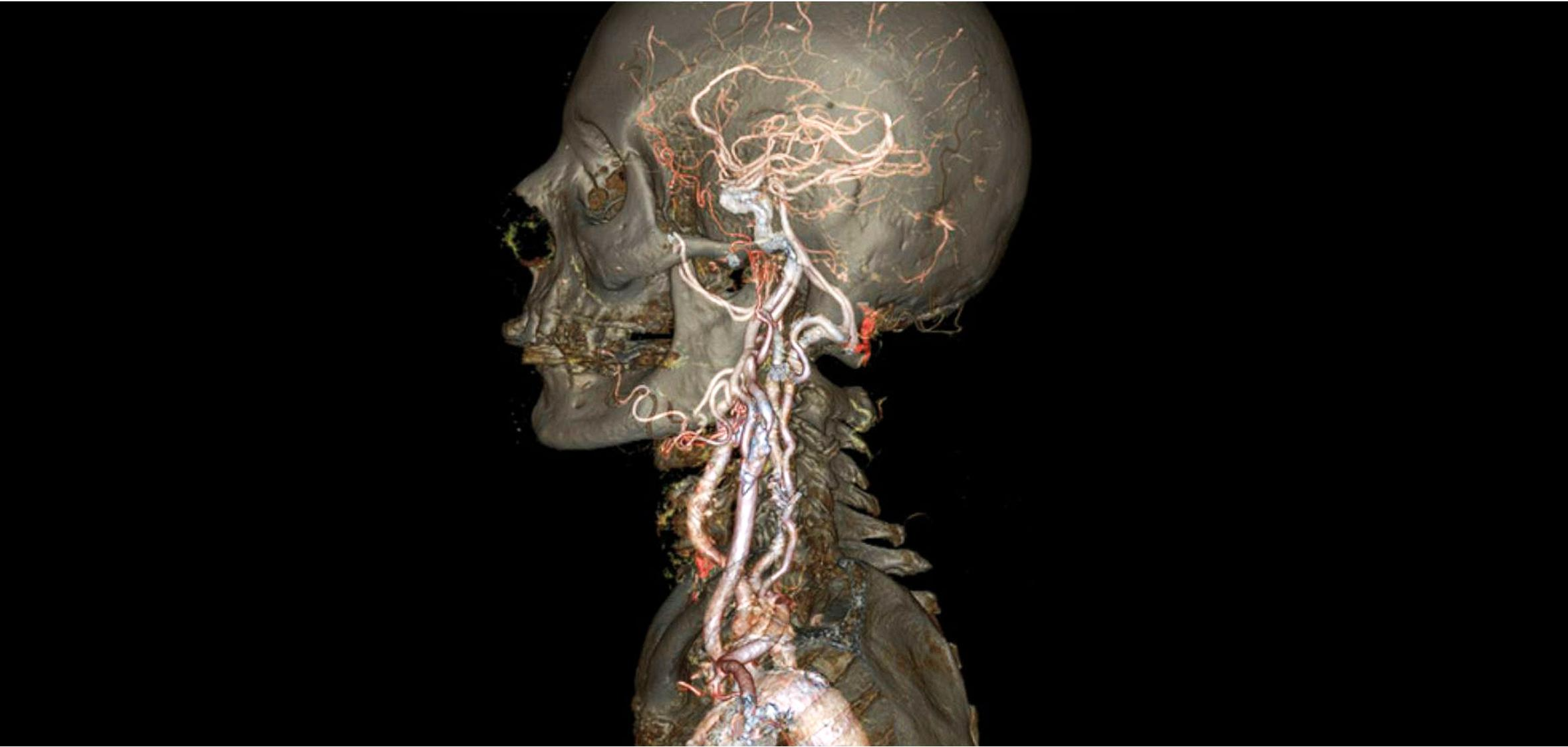
医学数据（CT、MRI等）的水平集。

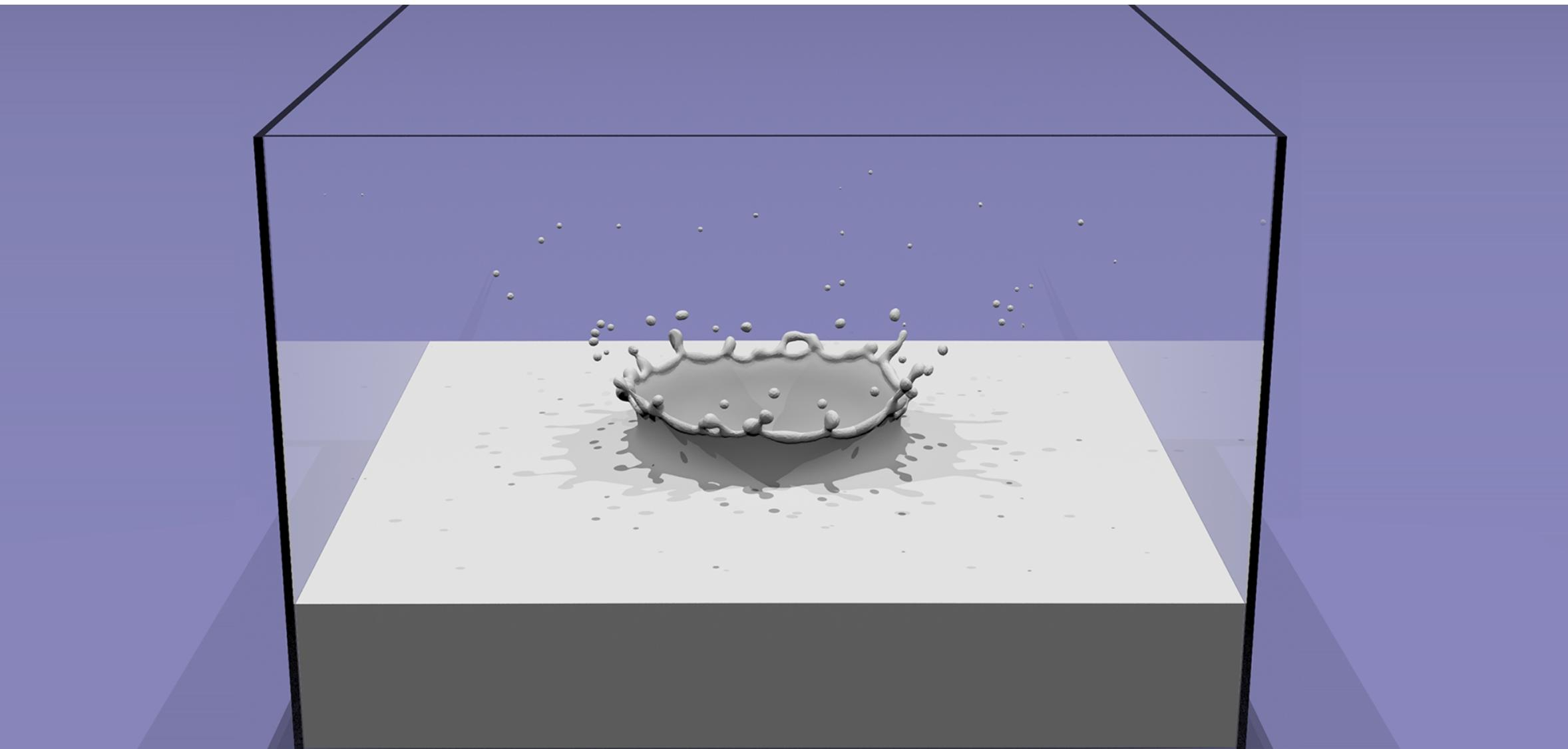
物理模拟中的水平集：水平集编码气液边界的距离。

5️⃣ 分形（Fractals (Implicit)）

表现出自相似性，在所有尺度上都有细节，描述自然现象的"语言"，形状难以控制！

6️⃣ 隐式表示优缺点（Implicit Representations - Pros & Cons）

优点：

• 描述紧凑（如单个函数即可表示复杂形状）；
• 内部 / 外部判断、距离查询等任务高效；
• 支持光线与表面相交计算；
• 简单形状可精确描述，无采样误差；
• 易于处理拓扑变化（如流体流动）；

缺点：

• 复杂形状的建模难度高。

三、疑难点整理总结

待补充。

写在最后

💗 感谢各位 📖 读者的支持，如果觉得文章对你有用，请 ♥️ 点赞 🌟 收藏，笔者将不胜感激 🌹～