目录
[3.1 时域影响](#3.1 时域影响)
[3.2 频域影响](#3.2 频域影响)
[4.1 整数偏移](#4.1 整数偏移)
[4.2 小数偏移](#4.2 小数偏移)
[4.3 MATLAB模拟采样率偏差](#4.3 MATLAB模拟采样率偏差)
1.理想采样过程
根据奈奎斯特采样定理,对一个最高频率为fm的连续时间信号x(t),理想采样率fsideal 需满足fsideal≥2*fm。

在离散域,理想采样信号的序列为:
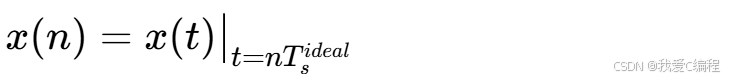
2.采样率偏差的物理本质
通信系统中,发射端和接收端的采样时钟由独立晶振驱动,晶振的频率误差会导致双方采样频率不一致,若发射采样率Fs,tx≠接收采样率Fs,rx,接收端会对发射信号产生"采样点拉伸/压缩",即采样率偏差。
而实际采样率fsactual(fsactual=Fs,rx)与理想采样率fsideal(fsideal=Fs,tx)存在偏差,定义:
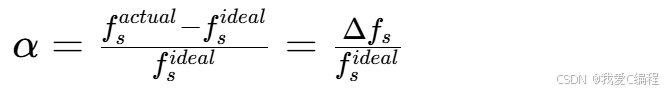
α为采样率偏差系数, α>0 表示实际采样率高于理想值(采样周期偏小), α<0表示实际采样率低于理想值(采样周期偏大)。
采样率绝对偏差定义为:
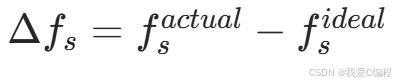
对应的实际采样周期为:
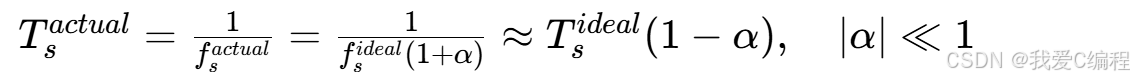
当∣α∣≪1时,可通过泰勒展开近似,该近似在绝大多数工程场景中成立。
3.采样率偏差对信号的影响
采样率偏差的本质是离散时间序列的时域尺度变换,具体影响分为时域和频域两个维度:
3.1 时域影响

3.2 频域影响

从上面的公式可知,实际采样序列的频谱是理想频谱的线性缩放,等效于信号的载波频率或基带信号频率发生偏移,这种偏移在通信系统中会导致载波同步误差,在数据采集中会导致频谱失真。 若采样率偏差过大,还会破坏奈奎斯特条件,导致频谱混叠,即高频分量折叠到基带,无法通过滤波恢复原始信号。
4.如何通过MATLAB来模拟信号的采样率偏差
由于采样率偏差通过累积效应,最终表现为时间偏移(时偏),二者的耦合关系是通信位同步的核心理论,采样率Fs与采样周期Tsamp满足倒数关系:
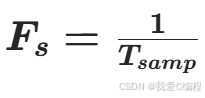
若存在采样率偏差ΔFs,则采样周期偏差为ΔTsamp,满足:
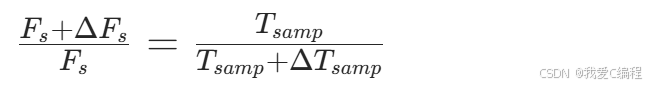
对其积分(偏差累积),得到时间偏移随符号数的变化关系:
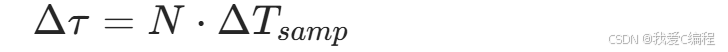
假设err是采样率偏差系数,将上述物理定律简化为工程可实现的耦合公式,即:
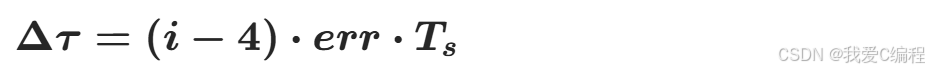
结合模运算归一化到单个符号周期:

然后我们以一个符号4倍采样为例,介绍如何通过MATLAB来模拟采样率偏差
4.1 整数偏移
以单个采样点的时长为最小单位的偏移,偏移量为采样点个数,取值为整数,记作noff。
noff∈{0,1,2,3}
也就说,我们可以通过1个符号的4个采样点,发生循环移位(整体偏移1/2/3个采样点);
select = mod(datano, nsamp)
上述公式的结果直接决定整数时偏大小,我们通过分别设置0个偏差,1个偏差,2个偏差,3个偏差来模拟对应的始终情况的整数时偏。即:
select=0(无整数时偏):采样点按"1→2→3→4"顺序赋值;
select=1(偏移1个采样点):采样点按"4→1→2→3"循环赋值;
select=2(偏移2个采样点):采样点按"3→4→1→2"循环赋值;
select=3(偏移3个采样点):采样点按"2→3→4→1"循环赋值。
4.2 小数偏移
偏移量小于单个采样点的时长,是采样点内部的精细偏移,取值为0~Ts之间的小数。小数时偏则可以通过如下的公式来表示:
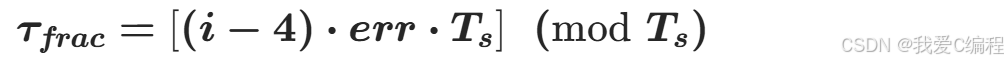
上述公式中:
**(i−4):**有效符号索引,表示当前处理的是第几个基带符号,为时偏的累积效应;
**err:**时偏系数,即单位符号的时偏量,是用户自定义的偏差强度;
**Ts:**符号周期,是时偏的归一化上限;
**mod(⋅,Ts):**模运算核心作用,强制小数时偏始终落在[0,Ts)区间内,保证偏移仅存在于单个符号周期内部,符合时偏的物理约束。
4.3 MATLAB模拟采样率偏差
根据上述的原理,我们编写如下的MATLAB程序:
clc;
clear;
close all;
warning off;
addpath(genpath(pwd));
rng('default');
len = 10000; %符号数
Freq_Data = 8e6; %符号速率
nsamp = 4; %采样倍数
Freq_Sample = Freq_Data * nsamp; %采样频率
Ts = 1 / Freq_Sample; %采样周期
T = nsamp * Ts; %符号周期
%信号加载的时偏
SNR_DBs = [20];
err1 = 0;
err2 = 1e-2;
err3 = 1e-1;
SNR_DB = SNR_DBs;
I_Data = double(rand(len,1)>=0.5)*2-1;
%经过根升余弦滤波器
I_D1 = u_rrcsend(I_Data,len,nsamp,err1,Ts);
I_D2 = u_rrcsend(I_Data,len,nsamp,err2,Ts);
I_D3 = u_rrcsend(I_Data,len,nsamp,err3,Ts);
%系统最后输出数据与原始数据比对
figure;
subplot(411);
stem(I_Data(3:end));
grid on;
xlim([0,60]);
legend('原始信号');
subplot(412);
stem(I_D1(1:nsamp:end));
grid on;
xlim([0,60]);
legend('时偏=0');
subplot(413);
stem(I_D2(1:nsamp:end));
grid on;
xlim([0,60]);
legend('时偏=1e-2');
subplot(414);
stem(I_D3(1:nsamp:end));
grid on;
xlim([0,60]);
legend('时偏=1e-1');
%系统最后输出数据与原始数据比对
figure;
subplot(411);
stem(I_Data(3:end));
grid on;
xlim([470,530]);
legend('原始信号');
subplot(412);
stem(I_D1(1:nsamp:end));
grid on;
xlim([470,530]);
legend('时偏=0');
subplot(413);
stem(I_D2(1:nsamp:end));
grid on;
xlim([470,530]);
legend('时偏=1e-2');
subplot(414);
stem(I_D3(1:nsamp:end));
grid on;
xlim([470,530]);
legend('时偏=1e-1');上述程序中,子函数u_rrcsend.m会在下一个小节课程中给出完整程序。
运行上述程序,我们可以得到如下的仿真结果:
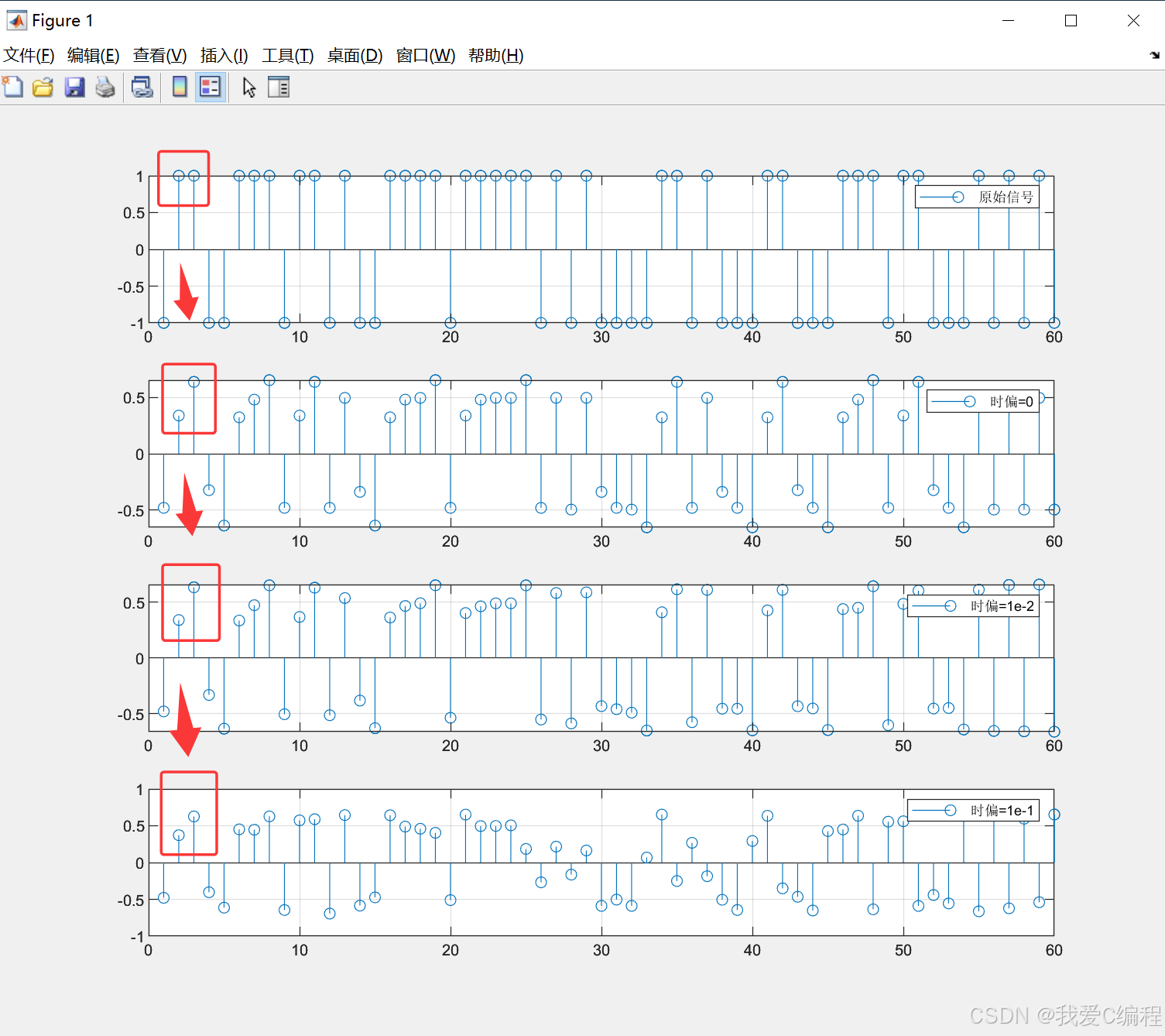
如上图所示,当数据在起始阶段,不同时钟偏差影响下,数据的采样点符号基本和初始的数据符号一致。
随着时间的推移,采样点改变如下:
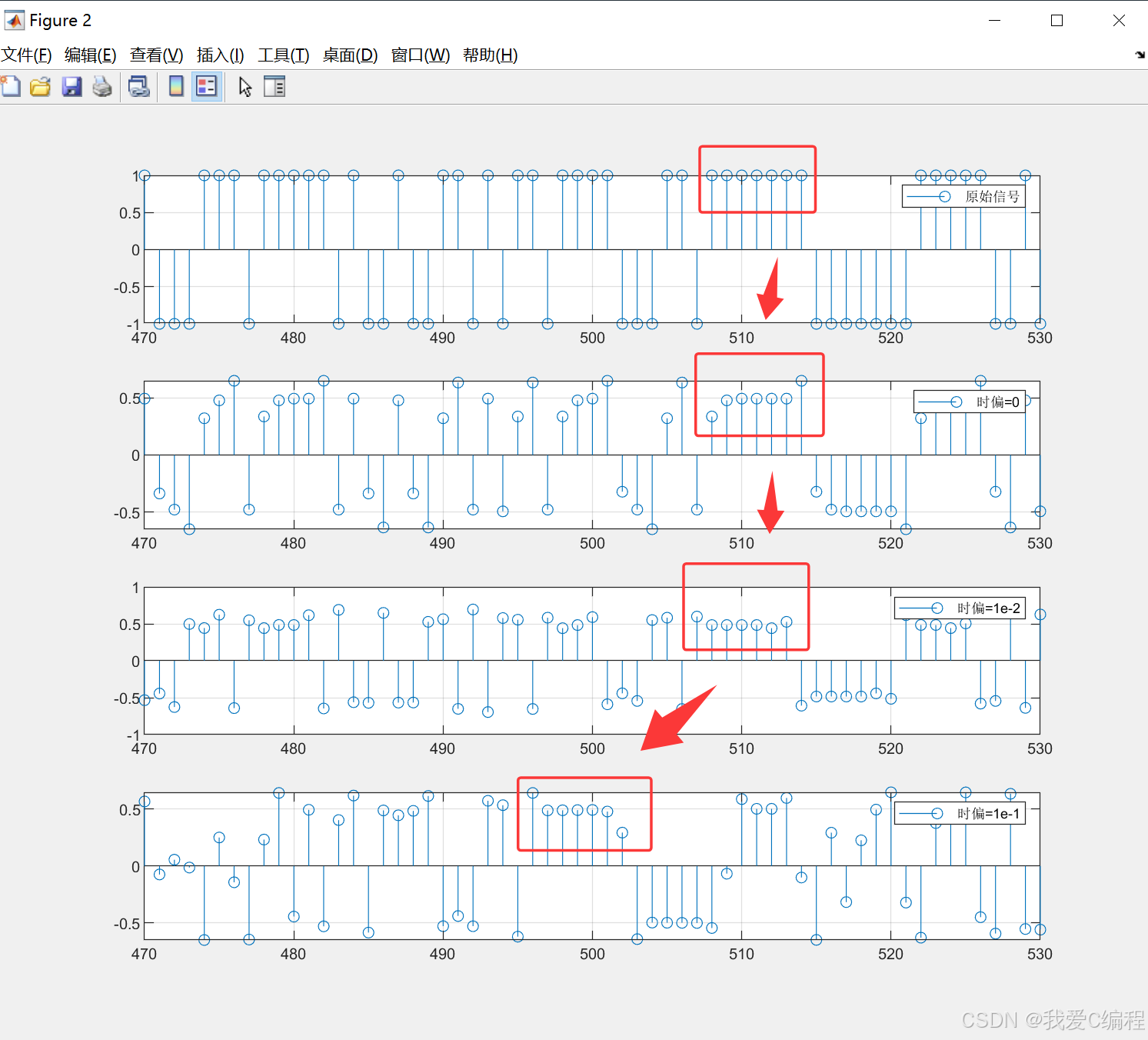
当时偏=0时,没有采样率偏差,此时,数据采样点和原数据一致,没有偏差。
当时偏=1e-2时,由于接收时钟比发射时钟快,因此采样点比原数据提前了1个采样点。
当时偏=1e-1时,由于接收时钟比发射时钟快,因此采样点比原数据提前了11个采样点。
可以看到,时偏=1e-1的采样点偏差,刚好为时偏=1e-2的采样点偏差的十倍,符合实际采样点偏差情况。