数据类型
首先我们先理解在计算机中是如何存储数据的,计算机的内存内存是一块连续的、可寻址的存储空间,每一个最小存储单元(字节)都有唯一的内存地址(通常用十六进制表示),数据必须存储在指定的内存地址中才能被 CPU 读取和操作。而变量的本质,是给存储数据的内存地址起的一个可读名字,所有编程语言都遵循这个底层规则。
数据类型
数据类型的作用是 表示数据在内存中的存储形式
Java 的核心设计目标之一是屏蔽底层内存操作(避免指针滥用的风险),基于计算机通用存储规则重新封装了变量的存储逻辑。
Java 是一种强类型的语言,声明变量时必须指定类型,核心作用是告诉 JVM 为这个变量分配多少内存、按什么规则存储/解析数据。
java 数据类型分为两大核心类别:
- 基本数据类型:变量直接存储数据本身,存储的是存储数据的地址,占用固定字节;
- 引用数据类型:变量存储的是实际数据的内存地址(引用),而非数据本身,默认值null表示无有效引用。
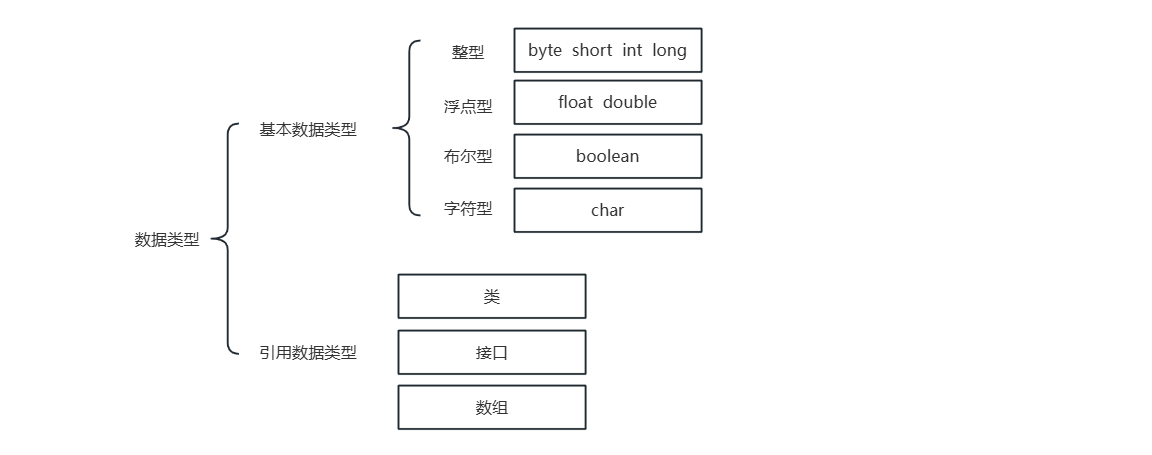
本篇博客主要讲解基本数据类型的相关内容
八种基本数据类型
八种基本数据类型的存储需求以及取值范围如图
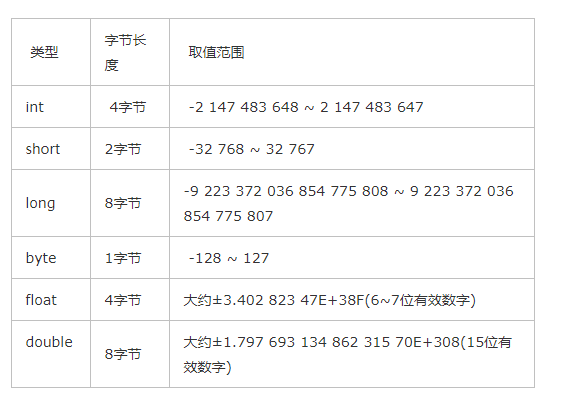
(注意这里 int 类型刚好超过20亿)
字节(B):字节是计算机信息技术用于计量存储容量和传输容量的一种计量单位,1个字节等于8位二进制,即 1Byte(字节) = 8bit(位)
数值型
一、数值型数据的进制:
十进制是默认进制,编程语言中默认不添加前缀的数字就是十进制;
八进制和十六进制的数字范围与十进制有重叠,为了让程序明确识别,需要给非十进制的数值添加特定前缀:
八进制用 0 开头(比如 012 表示八进制的 12,转换为十进制是 10),十六进制用 0x 或 0X 开头(比如 0x12 表示十六进制的 12,转换为十进制是 18),二进制用 0b 或 0B 开头(比如 0b10 表示二进制的 10,转换为十进制是 2)。
二、数值型数据的原码、反码和补码
我们需要知道的是在计算机内存 / 寄存器中,整数型数据的二进制存储形式唯一且固定为补码,而原码和反码只是计算补码的中间过程,不会被存储。
下面以 byte 类型举例
- 原码:45:00101101, -45:10101101
在最高位代表符号位区分正数还是负数,0代表正数,1代表负数 - 反码:45:00101101, -45:11010010
正数的原码和反码相同,负数的反码等于原码的符号位不变,其余各位按位取反 - 补码:45:00101101, -45:11010011
正数的原码反码和补码都形同,负数的补码等于在其反码基础上末尾+1
问题1:为什么计算机设计反码和补码?
首先我们需要知道计算机只有加法没有减法,在做减法运算的时候,可以认为是加上一个负数,这样可以减少计算机电路的复杂度。
这样使用原码进行减法运算会出现问题,例如计算1-1会将其自动换算成1+(-1)
若计算机存储的是原码,1-1=1+(-1)=[00000001]原+[10000001]原=[10000010]原=-2 ,与结果不符;
若计算机存储的是反码,1-1=1+(-1)=[00000001]原+[10000001]原=[00000001]反+[11111110]反=[11111111]反=[10000000]原=-0,正确;
但是我们发现这样就产生了一个问题:00000000代表+0,10000000代表-0,数值都是0但用两个编码属实浪费,于是便出现了补码,解决了0的符号以及编码的问题。
计算机存储的是补码,1-1=1+(-1)=[00000001]原+[10000001]原=[00000001]补+[11111111]补=[00000000]补=[00000000]原=0
总结:反码的出现是为了解决减法运算,补码的出现是为了解决反码产生的±0的问题
问题二:为什么 byte 类型 127+1 是 -128 ?
先看下图

使用补码不仅解决了原码 / 反码中0的冗余编码问题,还将这一冗余编码重新分配给了绝对值更大的负数,因此补码能多表示一个最小值。这也是为什么:
8 位二进制中,原码 / 反码因 符号位+7位数值位 的限制,且- 0占用了10000000编码,只能表示 [-127, 127],而补码取消了- 0,将1000 0000定义为-128的编码,因此范围扩展为 [-128, 127];
32 位有符号 int 类型的最高位为符号位,正数的数值位最大为 2³¹-1,而符号位为 1 的冗余编码1000...0000被分配给 - 2³¹,因此其表示范围为 [-2³¹, 2³¹-1]。
浮点类型
首先我们来看一下浮点类型在计算机中是如何存储的
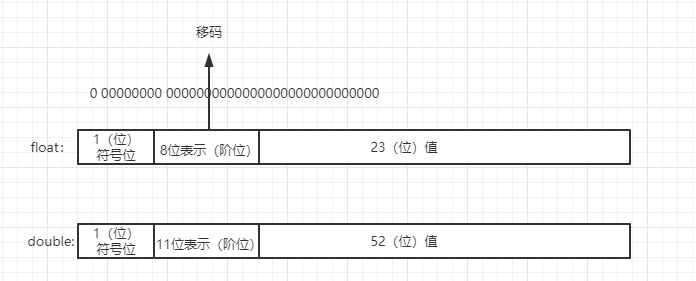
浮点数遵循 IEEE 754 标准:
float 存储需求是4字节(32位),其中1位最高位是符号位,中间8位表示阶位,后32位表示值
double 存储需求是8字节(64为),其中1位最高位是符号位,中间11位表示阶位,后52位表示值
适合使用 float 的场景:
对精度要求较低,对计算速度要求高于精度的场景。
适合使用 double 的场景:
对精度要求较高:如金融交易(金额需精确到分,且大额资金需多位数有效数字)、科学计算、高精度计量;
避免累计舍入误差:如迭代计算、大数据量的数值运算(float 的舍入误差易随计算次数放大);
大部分通用应用程序:如企业级系统、数据分析、编程语言默认浮点类型(Python/Java 等默认浮点运算为 double)。
下面详细讨论浮点类型的精度丢失问题和解决方案
浮点类型的精度丢失并非编程语言缺陷,而是IEEE 754 二进制浮点编码的固有数学特性,核心源于两大底层约束:
- 进制转换的数学限制:二进制仅能精确表示分母为 2 的整数次幂的十进制小数,对于分母包含 2 以外质因数的十进制小数,转换为二进制后会成为无限循环小数,这是进制本身的特性,如同十进制无法精确表示 1/3(0.333...);
IEEE 754 尾数的硬性存储限制:IEEE 754 为浮点数的尾数(有效数字位)设定了固定长度,无法存储无限循环的二进制小数,因此必须对循环部分截断或舍入,最终存储的是近似值而非数学上的精确值,这是精度丢失的直接原因。
java
public class SimpleTest {
public static void main(String[] args) {
System.out.println(1.2 - 1);
}
}输出结果为 0.19999999999999996 而并非 0.2
二进制仅能精确表示分母为 2 的整数次幂的十进制小数,对于分母含 2 以外质因数的十进制小数,转换为二进制后会成为无限循环小数,这是进制本身的数学特性,如同十进制无法精确表示 1/3(0.333...);
并且 IEEE 754 对浮点数的尾数位数做了硬性限制,对于无限循环的二进制小数,必须截断或舍入到指定位数,最终存储的是近似值而非精确值,这是精度丢失的直接原因。
由于二进制浮点存储的近似性,float/double完全不适用于禁止任何舍入误差的场景(如金融结算、金额计算、税务核算等),这类场景要求十进制数值的精确运算,而二进制浮点的舍入误差会导致分/厘级的计算错误,严重影响业务准确性。
若需实现无舍入误差的十进制数值运算,应使用 Java 的 java.math.BigDecimal类
BigDecimal 是将十进制数值存储为「整数标量 + 十进制缩放因子」(例如 0.2 存储为整数 2 + 缩放因子 10⁻¹,1.2 存储为整数 12 + 缩放因子 10⁻¹),运算时基于十进制算术规则计算,从根本上避免了二进制进制转换的循环问题,因此能保证十进制数值的精确运算。
java
public static void main(String[] args) {
BigDecimal b1 = new BigDecimal(Float.toString(1.2f));
BigDecimal b2 = new BigDecimal(Float.toString(1));
float s = b1.subtract(b2).floatValue();
System.out.println("s----" + s);
}输出结果为:s----0.2
字符类型
一、基础属性
Java 基本数据类型中的 char 是16 位无符号整数类型,固定占用 2 字节内存空间,取值范围为十进制 0(对应十六进制转义符 \u0000)到十进制 65535(对应十六进制转义符 \uffff),无负数取值。
二、编码核心逻辑
理解char的字符表示能力,需先明确几个核心术语:
Unicode 码点(Code Point):Unicode 字符集中为每个字符分配的唯一数值标识,取值范围为U+0000 ~ U+10FFFF,覆盖全球绝大多数语言字符、符号及表情符号。
UTF-16 编码:将 Unicode 码点转换为计算机可存储的二进制形式的主流编码规则,其核心是把码点映射为 1 个或 2 个码元(Code Unit)。其中,码元是 UTF-16 编码的最小存储单元(固定为 2 字节),码元值指码元中存储的 16 位整数值。
Java 的 char 类型:本质等价于 UTF-16 编码的 1 个码元,其内存中存储的核心内容为该码元对应的 16 位整数值(即码元值)。
三、字符表示规则(按 Unicode 平面划分)
Unicode 字符集按码点范围分为基本多文种平面和增补平面,char 对两类字符的表示能力存在显著差异:
- 基本多文种平面(BMP)的码点范围为 U+0000 ~ U+FFFF,单个 char 可完整存储该字符对应的 UTF-16 码元(码元值 = 码点值),即单个char可独立表示一个完整的 BMP 字符;
典型示例:英文字母(U+0041对应 'A')、中文常用字(U+4E2D对应 ' 中')、阿拉伯数字(U+0030对应 '0')等。 - 增补平面字符的码点范围为 U+10000 ~ U+10FFFF,此类字符的 UTF-16 编码需 2 个码元;
通过两个连续的 char 组合完整存储该字符的 UTF-16 编码,进而表示对应的 Unicode 码点;
典型示例:生僻汉字(如U+20000)、emoji 表情(如U+1F600对应😀)、部分特殊符号等。
java
public static void main(String[] args) {
char c1 = '中';
char c2 = '\u4e2d';
System.out.println(c1);
System.out.println(c2);
}
char c1 = '中'的合法性:字符字面量'中'对应的 Unicode 码点为 U+4E2D,因该字符属于 BMP 范围,其 UTF-16 码元值与码点值一致,该码点值落在char的取值范围内,因此编译器可将该码元值直接赋值给 char 变量 c1,操作合法。
char c2 = '\u4e2d'的合法性:\u4e2d是 Java 的 Unicode 转义字符,编译器在词法分析阶段会直接将\u4e2d解析为十六进制整数0x4e2d,该值落在 char 的取值范围内,因此可直接赋值给 char 变量 c2,操作合法。
java
public static void main(String[] args) {
int a = '中';
System.out.println(a);
char c = 69;
System.out.println(c);
}输出结果为 20013 和 E
第一段:代码中赋值操作的底层逻辑
在代码 int a = '中' 中,字符字面量 ' 中' 对应的 Unicode 码点为 U+4E2D,该码点对应的十进制整数为 20013,编译器会直接将这个整数值赋值给 int 变量 a,而 char c = 69 则是直接将十进制整数 69 赋值给 char 变量 c,由于 20013 和 69 均落在 char 的取值范围内,赋值操作合法。这两个赋值操作仅形式不同,前者是字符字面量转整数,后者是直接赋整数,核心都是基于整数值的存储逻辑。
第二段:System.out.println () 方法的输出规则
System.out.println() 会根据传入参数的类型执行差异化的输出逻辑:当传入的是 int 类型变量 a 时,方法会直接输出变量中存储的整数值,因此 System.out.println(a) 会打印出 ' 中' 对应的十进制值 20013;当传入的是 char 类型变量 c 时,方法不会直接输出其存储的整数值 69,而是遵循 Unicode 字符集的映射规则,将 char 中存储的整数值 69 作为 UTF-16 码元值,查找 Unicode 编码表后,确定该值对应字符 'E',因此 System.out.println© 最终输出字符 'E'。这一差异体现了 char 类型 "存储为整数、展示为字符" 的核心特性,而 int 类型则始终直接体现数值本身。
四、转义字符
转义字符是 Java 中表示特殊字符的标准化语法:以反斜杠 \ 开头,后跟特定字符或十六进制数字组合
Java 中的转义形式主要分为两类,分别解决不同场景的字符表示问题:
- 普通转义字符(\ + 特定字符):本质是覆盖 / 改变后跟字符的原生语义
一是无法直接输入的控制字符,二是有语法特殊含义的字符(直接书写会被编译器解析为语法符号而非普通字符); - Unicode 转义序列(\u + 4 位十六进制数):属于特殊的转义形式,用于通过十六进制数直接指定字符的 Unicode 码点,这类转义是编译器在词法分析阶段直接将 \uXXXX 映射为对应码点的整数值,本质是数值层面的直接替换。
例如:
java
public static void main(String[] args) {
int num = 100;
String json = "{"+"\"count\":"+num+"}";
String dataString = "[{\"id\":\"1\" ,\"name\":\"张三\"},{\"id\":\"2\" ,\"name\":\"李四\"},{\"id\":\"3\" ,\"name\":\"王五\"}]";
System.out.println(json);
}输出结果为 {"count":100}
常用的控制字符转义
\n:换行符,输出时换行;
\r:表示换行符;
\t:Tab 键;
':单引号;
":双引号;
\:反斜杠( \ );
布尔类型
取值范围仅有两个内置字面量:true(表示 "真 / 成立")、false(表示 "假 / 不成立");
核心用途:用于逻辑判断(条件分支、循环控制),是程序流程控制的核心基础;
Java 是强类型语言,boolean 和 byte/short/int/long/float/double 之间无任何隐式 / 显式转换关系
间接关联数值的唯一方式是逻辑表达式
如果需要将数值和 boolean 关联,只能通过比较 / 逻辑运算得到 boolean 值。
强制类型转换
图中所标均为合法转换,实线箭头均为无信息丢失的转换,虚线箭头表示可能有精度丢失的转换
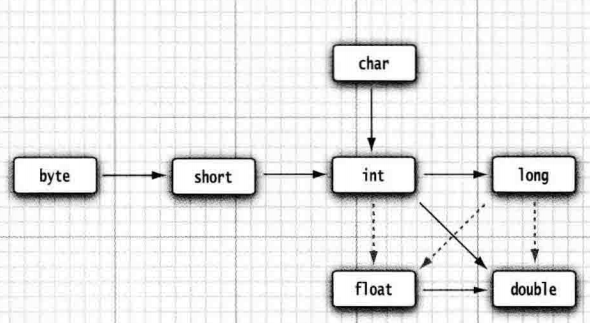
图中没标的转换形式需要经过强制类型转换才能做到,但是强制类型转换可能会造成精度丢失
我们来看以下代码:
java
public static void main(String[] args) {
byte a = 127;
byte b = (byte)(a+1);
System.out.println(b);
}数值运算的补码逻辑:byte 类型是 8 位有符号整数,取值范围为 [-128, 127],存储时遵循补码规则。127 的 8 位补码为 01111111,当执行a+1时,按补码运算:127+1=[01111111]补+[00000001]补=[10000000]补=-128(补),因此强制转换为 byte 后 b 的值为 - 128。
若直接写 byte b = a+1; 会编译报错,这是因为 Java 的整型提升规则,byte/short/char 类型参与算术运算时,会先自动提升为 int 类型(即使运算数是 byte 字面量),运算结果也必然是 int 类型,int 类型无法直接赋值给 byte 类型,编译器会提示 "不兼容的类型:从 int 转换到 byte 可能会有损失",必须通过 (byte) 强制截断为八位才能赋值,或者将接收参数改为 int 类型,直接存储 int 类型结果,无类型损失。
补充说明:上述是整型运算的类型规则,而浮点类型因二进制存储特性存在精度丢失问题,若需高精度十进制运算,可使用BigDecimal类,这是与整型运算完全不同的场景解决方案。
运算
这里主要介绍按位运算与移位运算
按位操作
按位与运算(&):
规则:二进制对应位都为 1 时结果位为 1,否则为 0
按位或运算(|)
规则:二进制对应位至少有一个为 1 时结果位为 1,否则为 0
按位异或运算(^):
规则:二进制对应位相同为 0,不同为 1
例题:有一个非空整数数组 nums,除了某个元素只出现一次以外,其余每个元素均出现两次,找出那个只出现了一次的元素。注意需要设计并实现线性时间复杂度的算法来解决此问题,且该算法只使用常量额外空间。
我们可以使用异或运算来解决该问题
假设数组中有 2m+1 个数,其中有 m 个数各出现两次,一个数出现一次,数组中的全部元素的异或运算结果总是可以写成如下形式:
(a1 ⊕ a1) ⊕ (a2 ⊕ a2) ⊕ ⋯ ⊕ (am ⊕ am) ⊕ am+1
上式可化简和计算得到如下结果:
0 ⊕ 0 ⊕ ⋯ ⊕ 0 ⊕ am+1 = am+1
因此,数组中的全部元素的异或运算结果即为数组中只出现一次的数字
java
public int singleNumber(int[] nums) {
int single = 0;
for(int i=0;i<nums.length;i++){
single ^= nums[i];
}
return single;
}移位运算
- 左移(<<):右边空出来的位用 0 填补高位左移溢出则舍弃该高位
左移几位就是这个数*2的几次幂 - 有符号右移(>>):左边空出来的位用 0 或 1 填补,正数用 0 负数用 1 填补。
右移几位就是这个数/2的几次幂 - 无符号右移(>>>):数据进行右移时,高位出现的空位,无论原高位是什么,空位都用 0 补
在 Java 中 byte、short 类型的整型变量在执行无符号右移运算时,会先自动提升为 int 类型,而 long 类型会按 64 位计算
移位运算与乘法运算的时间比较:
java
public static void main(String[] args) {
long startTime=System.nanoTime(); //获取开始时间
System.out.println(2*16);
long endTime=System.nanoTime(); //获取结束时间
System.out.println("程序运行时间:"+(endTime-startTime)+"ns");
long startTime1=System.nanoTime();
System.out.println(2<<4);
long endTime1=System.nanoTime();
System.out.println("程序运行时间:"+(endTime1-startTime1)+"ns");
}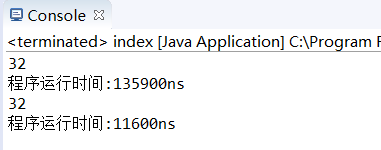
同样计算 2*16,移位运算与乘法运算的时间相差较大,有时乘法运算选择使用移位运算效率会更高