基于Matlab的改进的广义预测控制

π同学2025-12-28 16:16

前言

前文的广义预测控制的计算量太大、算法过于复杂，于是后面又提出里两种改进的广义预测控制。一种是基于CARIMA模型，和基本的广义预测控制使用的模型一致，还有一种是基于CARMA模型。

改进的广义预测控制具有算法简单、计算量小、不受矩阵C稳定的限制，在实际中运用更广。

一、CARIMA_GPC

下面先介绍基于CARIMA模型的改进的广义预测控制。

1.1 算法推理

受控自回归积分滑动平均模型（CARIMA ）如下：

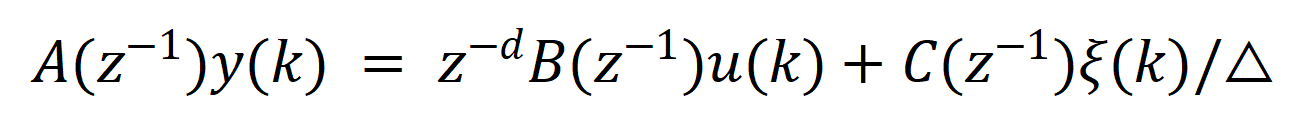
可化简成：

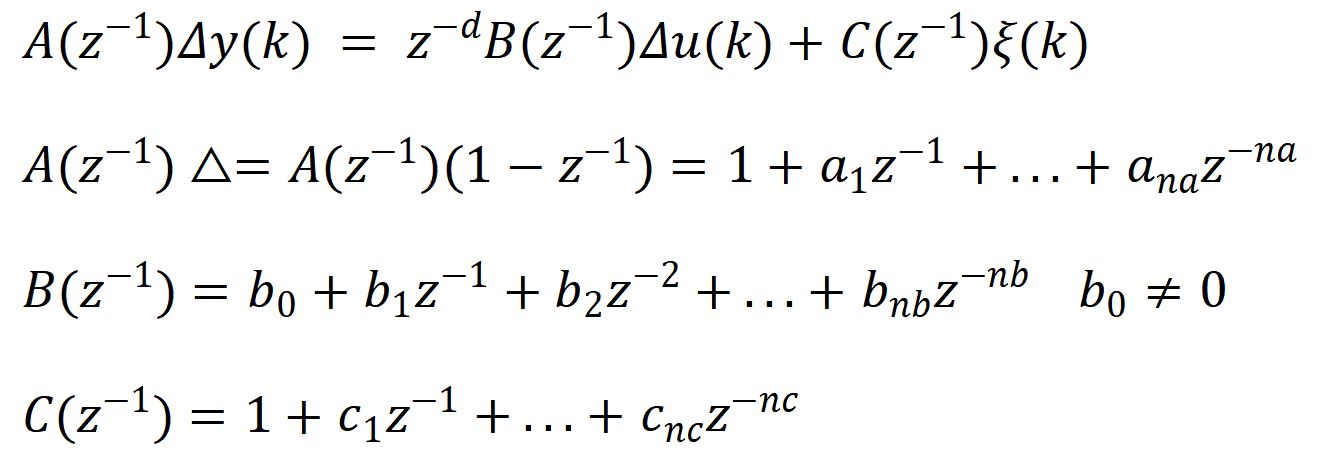
将来时刻的最小方差输出预测模型为：

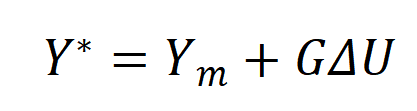
式中Y*为输出预测向量、Ym是一个调节向量、G是控制矩阵、U是控制增量向量

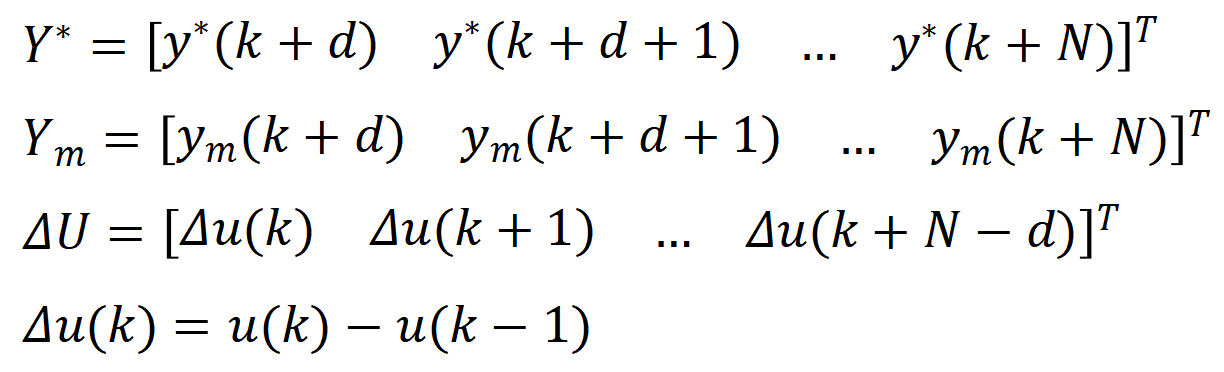
控制矩阵：

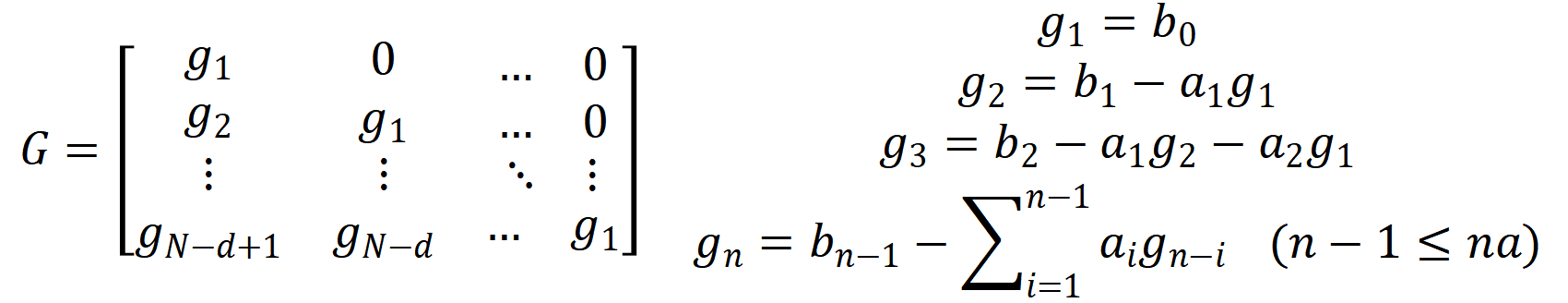
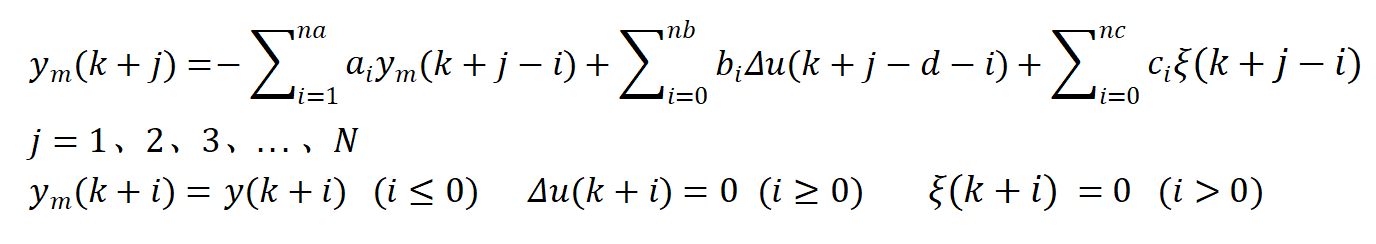其中的d是纯延时环节，N为预测长度。ym是由过去的控制输入和输出确定的

整个系统预测控制的性能指标为：

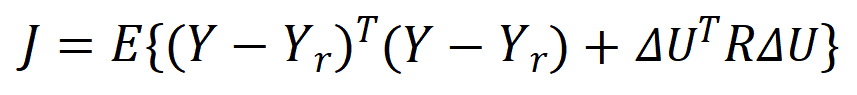
可得到控制律：

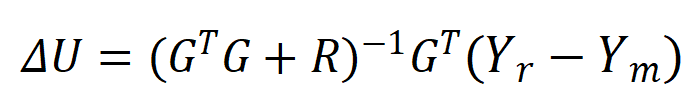
其中的Yr为参考轨迹向量：

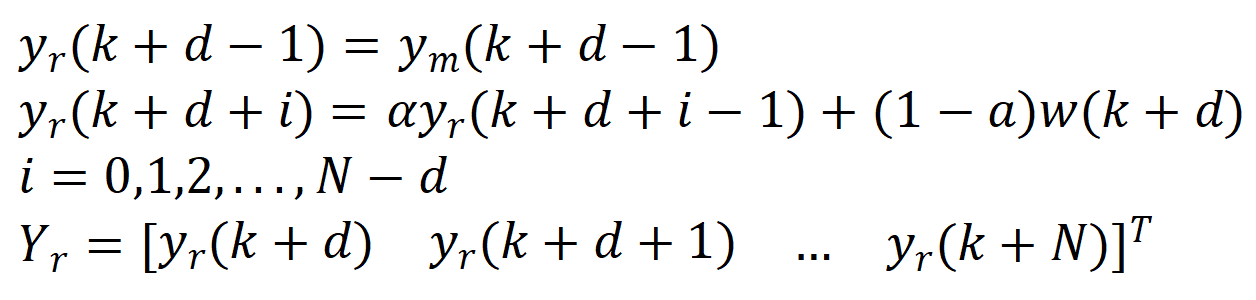
w(k)为k时刻的期望输出，为柔化系数。

综上计算的控制量：

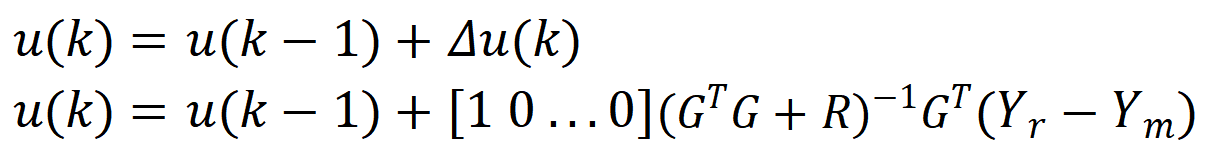
1.2 实例说明

有如下开环不稳定的非最小相位系统：

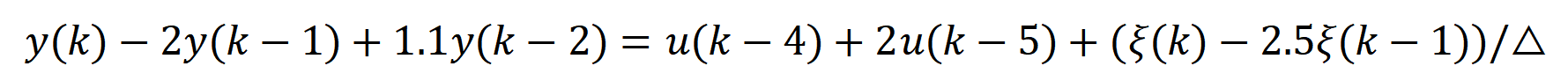
其中是方差为0.01的白噪声，上文的实例相同，只不过C(z)不等于1了，写成适合GPC控制的模型如下：

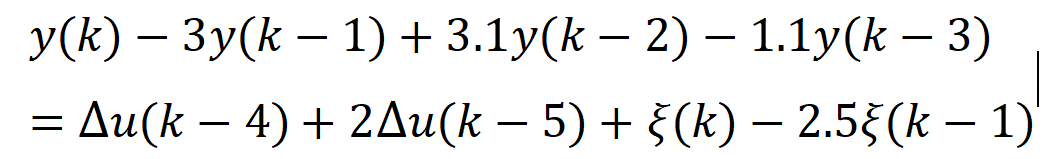
录入参数如下

Matlab 复制代码 
clear; close;
A = conv([1 -2 1.1],[1 -1]); B = [1 2]; C = [1 -2.5]; d = 4;
na = length(A)-1; nb = length(B)-1; nc = length(C)-1;

接下来确定预测长度N、仿真步长L、期望输出w和噪声信号u_noise。

Matlab 复制代码 
N = 8;
L = 600;
w = 10*[ones(1,L/4) -ones(1,L/4) ones(1,L/4) -ones(1,L/4+d)];%期望输出
u_noise = sqrt(0.1) * randn(1,L);%噪声信号

下面先计算控制矩阵G

Matlab 复制代码 
G = Gsolve(A,B,d,N);

%****************************************************************
  %功能：改进GPC控制矩阵G的求解（CARIMA模型）
  %调用格式：G=Gsolve(a,b,d,N)
  %输入参数：多项式A、B（行向量）、纯滞后和预测长度（共4个）
  %输出参数：控制矩阵G
%****************************************************************
function G=Gsolve(a,b,d,N)
    na=length(a)-1; nb=length(b)-1; %na是多项式A的阶次，nb是多项式B的阶次
    a1=a(2:na+1);
    
    G=zeros(N-d+1);
    G(1,1)=b(1);
    for j=2:N-d+1
        ab=0;
        for i=1:min(j-1,na)
            ab=ab+a1(i)*G(j-i,1);
        end
        if j<=nb+1
            b1j=b(j);
        else
            b1j=0;
        end
        G(j,1)=b1j-ab;
        for i=2:j
            G(j,i)=G(j-1,i-1);
        end
    end
end

接着就是主题代码，主要是计算调节向量Ym，参考轨迹向量Yr以及控制输入u(k)。对比上面的公式可以发现，我的代码完全就是复制公式，非常直观。这种写法非常适合各种算法实现。

Matlab 复制代码 
R = 1*eye(N-d+1); a = 0.7;
%让t=10设为0时刻,则之前的时刻方便表达
time = zeros(1,L);
y = zeros(1,L);
yr = zeros(1,L);
ym = zeros(1,L);
dU = zeros(1,L);
u = zeros(1,L);
t = 10;
for k=t:L-t
    time(k) = k-t+1;
    y(k) = -A(2:na+1)*[y(k-1);y(k-2);y(k-3)]+B*[dU(k-4) dU(k-5)]'+C*[u_noise(k) u_noise(k-1)]';
    ym(k) = y(k);
    for j = 1:N
         ym(k+j) = -A(2:na+1)*flip(ym(k+j-na:k+j-1))'+B*flip(dU(k+j-d-nb:k+j-d))'+C*flip(u_noise(k+j-nc:k+j))';
    end
    yr(k+d-1) = ym(k+d-1);
    for j = 0:N-d
        yr(k+d+j) = a*yr(k+d+j-1)+(1-a)*w(k+d);
    end
    Ym = [ym(k+d:k+N)]';
    Yr = [yr(k+d:k+N)]';
    dUK = (G'*G+R)\G'*(Yr-Ym);
    dU(k) = dUK(1);
    u(k) = u(k-1)+dUK(1);
    yr(k+N+1) = a*yr(k+N+1-1)+(1-a)*w(k+1+d);
end

结果输出

Matlab 复制代码 
figure;
subplot(2,1,1);
plot(time(t:L-t),w(t:L-t),'r:',time(t:L-t),y(t:L-t));
xlabel('k'); ylabel('w(k)、y(k)');
legend('w(k)','y(k)');
grid on;
subplot(2,1,2);
plot(time(t:L-t),u(t:L-t));
xlabel('k'); ylabel('u(k)');
grid on;

1.3 完整代码

Matlab 复制代码 
clear; close;
A = conv([1 -2 1.1],[1 -1]); B = [1 2]; C = [1 -2.5]; d = 4;
na = length(A)-1; nb = length(B)-1; nc = length(C)-1;
N = 8;
R = 1*eye(N-d+1); a = 0.7;
G = Gsolve(A,B,d,N);
L = 600;
w = 10*[ones(1,L/4) -ones(1,L/4) ones(1,L/4) -ones(1,L/4+d)];%期望输出
u_noise = sqrt(0.1) * randn(1,L);%噪声信号
%u_noise = zeros(1,L);
%让t=10设为0时刻,则之前的时刻方便表达
time = zeros(1,L);
y = zeros(1,L);
yr = zeros(1,L);
ym = zeros(1,L);
dU = zeros(1,L);
u = zeros(1,L);
t = 10;
for k=t:L-t
    time(k) = k-t+1;
    y(k) = -A(2:na+1)*[y(k-1);y(k-2);y(k-3)]+B*[dU(k-4) dU(k-5)]'+C*[u_noise(k) u_noise(k-1)]';
    ym(k) = y(k);
    for j = 1:N
         ym(k+j) = -A(2:na+1)*flip(ym(k+j-na:k+j-1))'+B*flip(dU(k+j-d-nb:k+j-d))'+C*flip(u_noise(k+j-nc:k+j))';
    end
    yr(k+d-1) = ym(k+d-1);
    for j = 0:N-d
        yr(k+d+j) = a*yr(k+d+j-1)+(1-a)*w(k+d);
    end
    Ym = [ym(k+d:k+N)]';
    Yr = [yr(k+d:k+N)]';
    dUK = (G'*G+R)\G'*(Yr-Ym);
    dU(k) = dUK(1);
    u(k) = u(k-1)+dUK(1);
    yr(k+N+1) = a*yr(k+N+1-1)+(1-a)*w(k+1+d);
end
figure;
subplot(2,1,1);
plot(time(t:L-t),w(t:L-t),'r:',time(t:L-t),y(t:L-t));
xlabel('k'); ylabel('w(k)、y(k)');
legend('w(k)','y(k)');
grid on;
subplot(2,1,2);
plot(time(t:L-t),u(t:L-t));
xlabel('k'); ylabel('u(k)');
grid on;
%****************************************************************
  %功能：改进GPC控制矩阵G的求解（CARIMA模型）
  %调用格式：G=Gsolve(a,b,d,N)
  %输入参数：多项式A、B（行向量）、纯滞后和预测长度（共4个）
  %输出参数：控制矩阵G
%****************************************************************
function G=Gsolve(a,b,d,N)
    na=length(a)-1; nb=length(b)-1; %na是多项式A的阶次，nb是多项式B的阶次
    a1=a(2:na+1);
    
    G=zeros(N-d+1);
    G(1,1)=b(1);
    for j=2:N-d+1
        ab=0;
        for i=1:min(j-1,na)
            ab=ab+a1(i)*G(j-i,1);
        end
        if j<=nb+1
            b1j=b(j);
        else
            b1j=0;
        end
        G(j,1)=b1j-ab;
        for i=2:j
            G(j,i)=G(j-1,i-1);
        end
    end
end

1.4 结果展示

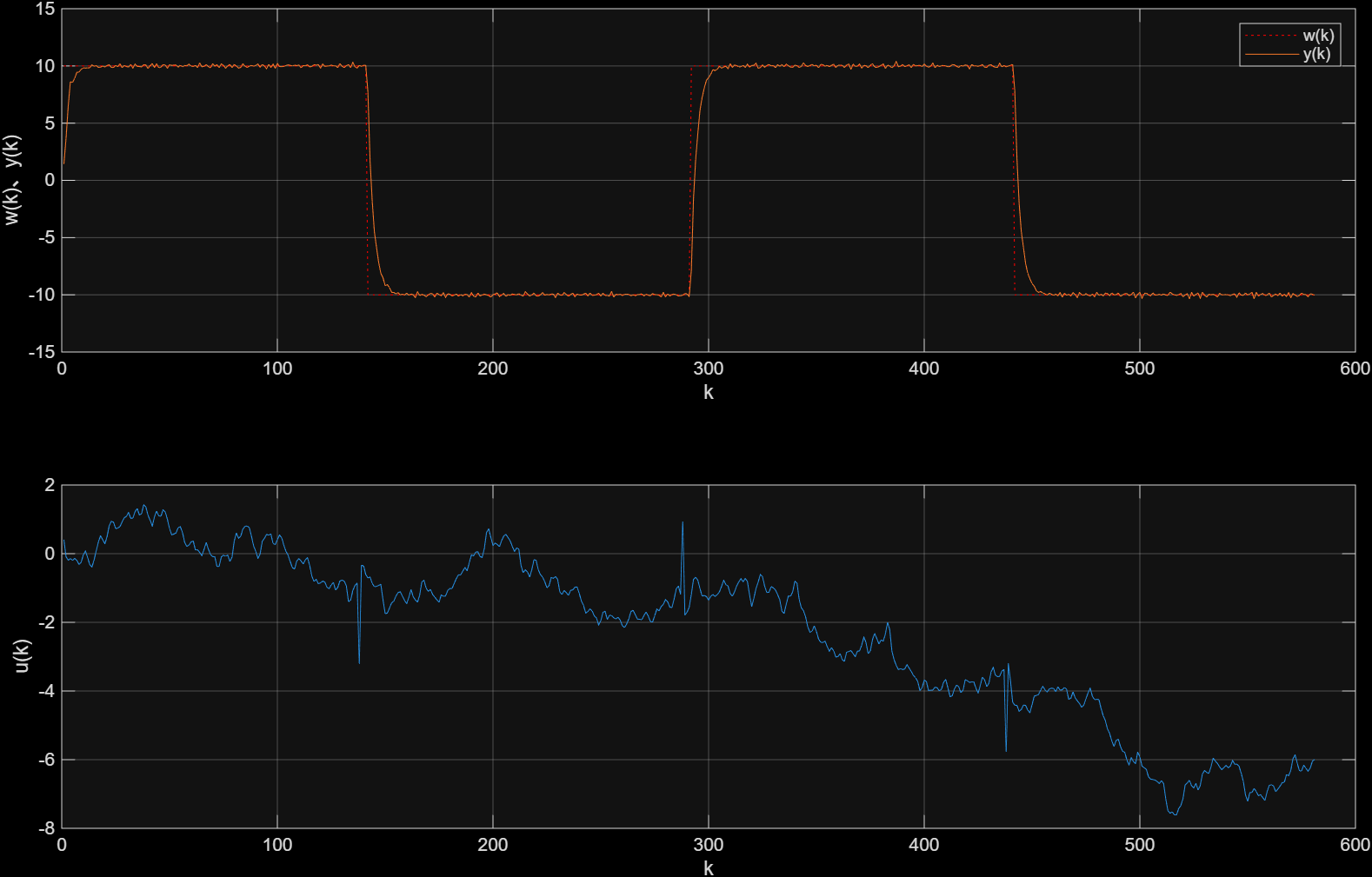
可以看出，控制效果非常好。在幅值为10的方波期望信号、方差为0.1的高斯噪声分布下，还是第一次理论上有这么好的跟踪效果

二、CARMA_GPC

接着是基于CARMA模型的改进的广义预测控制。大部分内容相同，就简化说明了。

2.1 算法推理

受控自回归滑动平均模型（CARMA ）如下：

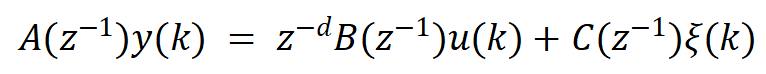
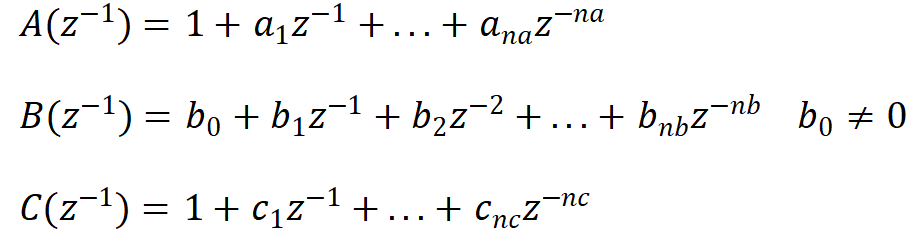
其他内容和CARIMA_GPC相同，调节向量Ym有所不同为：

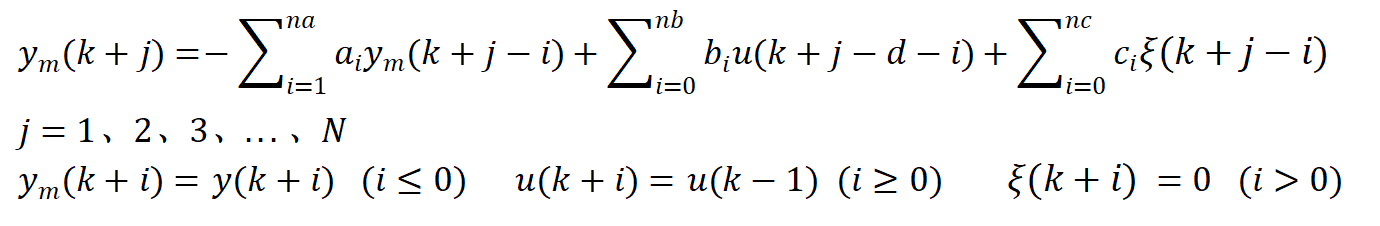
其中的d是纯延时环节，N为预测长度。ym是由过去的控制输入和输出确定的

2.2 实例说明

有如下开环不稳定的非最小相位系统：

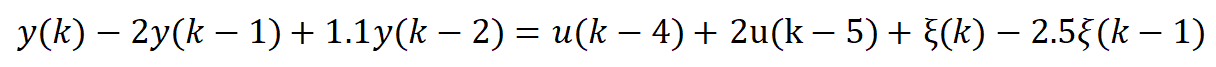
其中是方差为0.01的白噪声，与第一部分的实例相同，只不过没了差分算子

因为其他部分同上面相同，那自然代码也相同，只有实例方程和Ym有所区别，这部分代码如下：

Matlab 复制代码 
    y(k) = -A(2:na+1)*[y(k-1);y(k-2)]+B*[u(k-4) u(k-5)]'+C*[u_noise(k) u_noise(k-1)]';
    ym(k) = y(k);
    for j = 0:N-d
        u(k+j) = u(k-1);
    end
    for j = 1:N
        ym(k+j) = -A(2:na+1)*flip(ym(k+j-na:k+j-1))'+B*flip(u(k+j-d-nb:k+j-d))'+C*flip(u_noise(k+j-nc:k+j))';
    end

2.3 完整代码

Matlab 复制代码 
clear; close;
A = [1 -2 1.1]; B = [1 2]; C = [1 -2.5]; d = 4;
na = length(A)-1; nb = length(B)-1; nc = length(C)-1;
N = 8;
R = 1*eye(N-d+1); a = 0.7;
G = Gsolve(A,B,d,N);
L = 600;
w = 10*[ones(1,L/4) -ones(1,L/4) ones(1,L/4) -ones(1,L/4+d)];%期望输出
u_noise = sqrt(0.1) * randn(1,L);%噪声信号
%u_noise = zeros(1,L);
%让t=10设为0时刻,则之前的时刻方便表达
time = zeros(1,L);
y = zeros(1,L);
yr = zeros(1,L);
ym = zeros(1,L);
dU = zeros(1,L);
u = zeros(1,L);
t = 10;
for k=t:L-t
    time(k) = k-t+1;
    y(k) = -A(2:na+1)*[y(k-1);y(k-2)]+B*[u(k-4) u(k-5)]'+C*[u_noise(k) u_noise(k-1)]';
    ym(k) = y(k);
    for j = 0:N-d
        u(k+j) = u(k-1);
    end
    for j = 1:N
        ym(k+j) = -A(2:na+1)*flip(ym(k+j-na:k+j-1))'+B*flip(u(k+j-d-nb:k+j-d))'+C*flip(u_noise(k+j-nc:k+j))';
    end
    yr(k+d-1) = ym(k+d-1);
    for j = 0:N-d
        yr(k+d+j) = a*yr(k+d+j-1)+(1-a)*w(k+d);
    end
    Ym = [ym(k+d:k+N)]';
    Yr = [yr(k+d:k+N)]';
    dUK = (G'*G+R)\G'*(Yr-Ym);
    u(k) = u(k-1)+dUK(1);
    yr(k+N+1) = a*yr(k+N+1-1)+(1-a)*w(k+1+d);
end
figure;
set(gcf, "Theme", "dark");
subplot(2,1,1);
plot(time(t:L-t),w(t:L-t),'r:',time(t:L-t),y(t:L-t));
xlabel('k'); ylabel('w(k)、y(k)');
legend('w(k)','y(k)');
grid on;
subplot(2,1,2);
plot(time(t:L-t),u(t:L-t));
xlabel('k'); ylabel('u(k)');
grid on;
%****************************************************************
  %功能：改进GPC控制矩阵G的求解（CARIMA模型）
  %调用格式：G=Gsolve(a,b,d,N)
  %输入参数：多项式A、B（行向量）、纯滞后和预测长度（共4个）
  %输出参数：控制矩阵G
%****************************************************************
function G=Gsolve(a,b,d,N)
    na=length(a)-1; nb=length(b)-1; %na是多项式A的阶次，nb是多项式B的阶次
    a1=a(2:na+1);
    
    G=zeros(N-d+1);
    G(1,1)=b(1);
    for j=2:N-d+1
        ab=0;
        for i=1:min(j-1,na)
            ab=ab+a1(i)*G(j-i,1);
        end
        if j<=nb+1
            b1j=b(j);
        else
            b1j=0;
        end
        G(j,1)=b1j-ab;
        for i=2:j
            G(j,i)=G(j-1,i-1);
        end
    end
end

2.4 结果展示

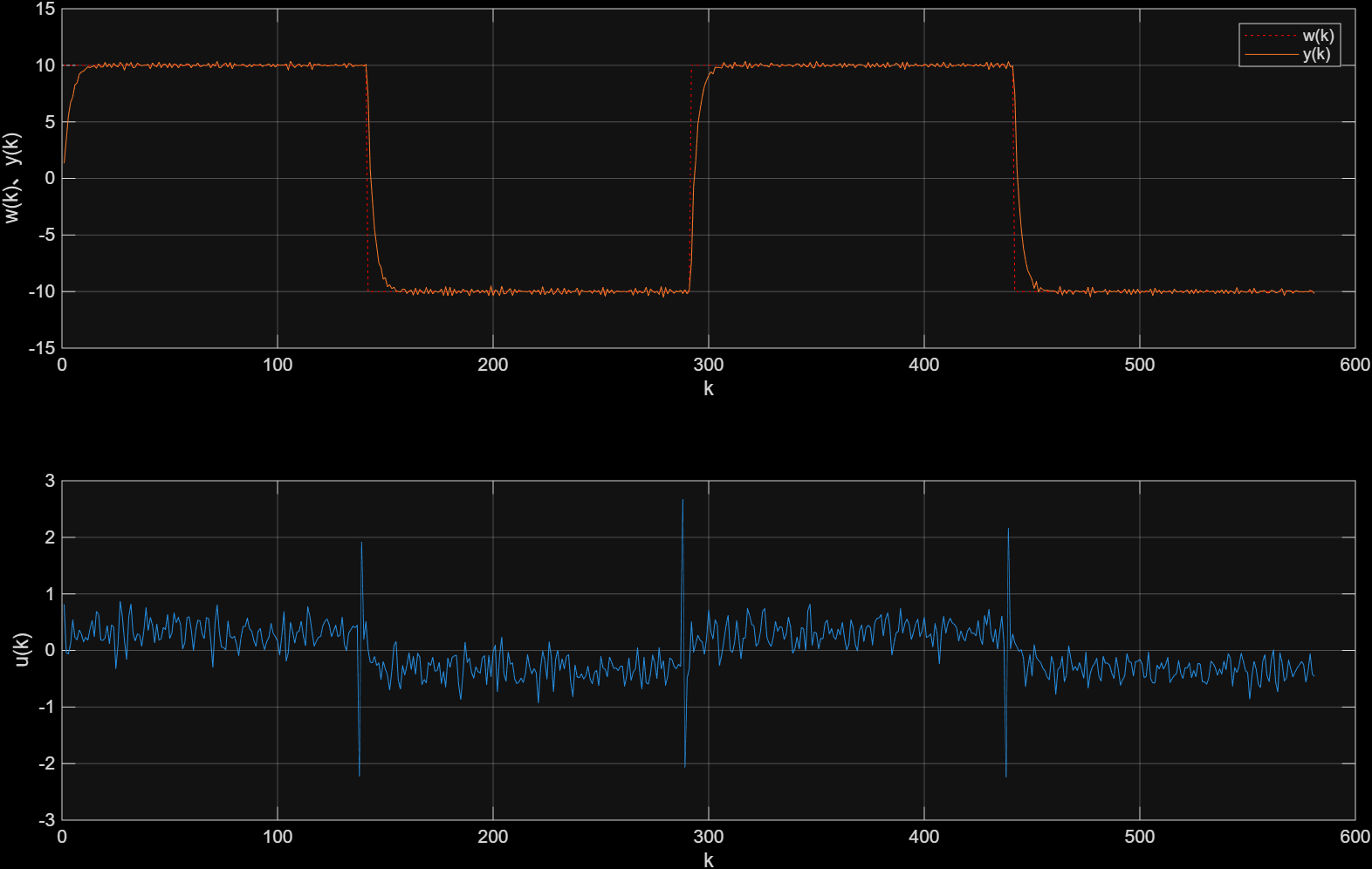
可以看出，控制效果与第一部分相同

相关推荐
IT猿手3 小时前
三维动态避障路径规划：基于部落竞争与成员合作算法（CTCM）融合动态窗口法DWA的无人机三维动态避障方法研究，MATLAB代码
算法·matlab·动态规划·无人机·路径规划·动态路径规划
freexyn3 小时前
Matlab速成笔记七十：使用多项式函数进行曲线拟合
开发语言·笔记·matlab
我找到地球的支点啦6 小时前
Matlab系列(006) 一利用matlab保存txt文件和读取txt文件
开发语言·算法·matlab
Dev7z6 小时前
基于Matlab实现GRACE卫星重力数据的全球水储量变化估算与分析
人工智能·算法·matlab
颖风船6 小时前
膨胀腐蚀及底层实践，拒绝opencv,matlab等方式
前端·opencv·matlab
杰瑞不懂代码6 小时前
基于 MATLAB 的 AM/DSB-SC/VSB 模拟调制与解调仿真及性能对比研究
开发语言·matlab·语音识别·am·dsb-sc·vsb
jllllyuz8 小时前
MATLAB多目标优化：SQP算法实现
数据结构·算法·matlab
我爱C编程10 小时前
【2.2】采样率偏差的基本数学原理概述与MATLAB模拟仿真
matlab·采样率偏差
bu_shuo1 天前
MATLAB中的转置操作及其必要性
开发语言·算法·matlab
热门推荐
01GitHub 镜像站点02从快手“12·22”直播攻击事件看：一次教科书式的业务层饱和攻击03电脑检测软件—图吧工具箱04Web安全中SQL注入绕过WAF的具体手法和实战案例05Linux下V2Ray安装配置指南063D 圣诞树网页代码07UV安装并设置国内源08SQLmap 完整使用指南：环境搭建 + 命令详解 + 实操案例09jdk21下载、安装（Windows、Linux、macOS）10在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）