前言
傅里叶变换能通过将信号的时域变换到信号的频域,因为在频域中,系统的响应就等于信号与系统传函的频域上相乘(时域上是卷积),相比于直接在时域里做卷积,先进行傅里叶变换,再在频域上相乘,最后通过逆傅里叶变换反变换回来的步骤看似更长更复杂,但在工程技术上却相对容易实现。
传统的傅里叶变换属于工程数学范畴,主要针对连续时间信号进行时域-频域的变换。而从工程技术的角度来看,人们不可能做到对信号进行连续时间的采样,因此离散傅里叶变换(DFT)也就在这种情况下诞生了。时间久了以后,人们发现DFT的算法时间复杂度太高了,优化DFT的迫在眉睫,快速傅里叶变换(FFT)的出现使原本时间复杂度o(n^2)的DFT直接降到了o(nlogn)。
以上算是FFT的极简版背景故事,具体如何发展如何变换的,数字信号处理相关课程一定有讲,这里就暂时不细讲了,这里还是主要以FPGA中实现快速傅里叶变换为主。
由于我仅在FPGA上实现FFT对信号进行时域-频域的变换,并做到了基波频率的采集,目前尚未如之前的一些历程那样试过其他的方案,因此本文不能给大家带来详细的FFT在FPGA上的实现,只是我在今年7月中下旬为准备TI杯那会调试出来的一种可行的方案。即便现在回看不觉得都有多少困难,但半年前那会真的困了我好久,弄出心理阴影来了给我,敬请谅解。
一、原理与目的
本来其实是不太想着重写原理的,但是考虑到没有特别学过数字信号处理和信号与系统的同学对傅里叶变换和快速傅里叶变换的认识不全面,这里我还是简单讲一下(前几篇感觉有点水文章了)。
1.傅里叶变换
傅里叶变换是将任意信号通过多种不同频率的正弦信号叠加而成。不同频率的正弦信号不仅有不同的频率,还有不同频率对应的幅值,通过频率与幅值的一一对应,就能得到任意信号的幅频特性曲线。
2.快速傅里叶变换
在傅里叶变换的基础上加入了对离散时间信号的应用,即离散傅里叶变换;对离散傅里叶变换的算法进行优化,得到了快速傅里叶变换(FFT)。
我在数字信号处理的课程上以知识点总结的名义讲过FFT的运算,具体的原理方面的讲得一定没有专业的老师好,但是最后的目的还是会计算方法、要算对(国内要求)。FFT的核心是蝶形运算和旋转因子,都在下面我自己写的纸上。这里我是用基2的8点FFT进行的距离,16点甚至更高的点数就不向下延伸了,注意事项就是时域抽取和频域抽取的关系是在单向运算(单向正变换或单向反变换)中的两种不同的运算方法。重点关注一下二进制逆序排列的操作,时域抽取、频域抽取上哪里需要进行二进制的逆序排列等。
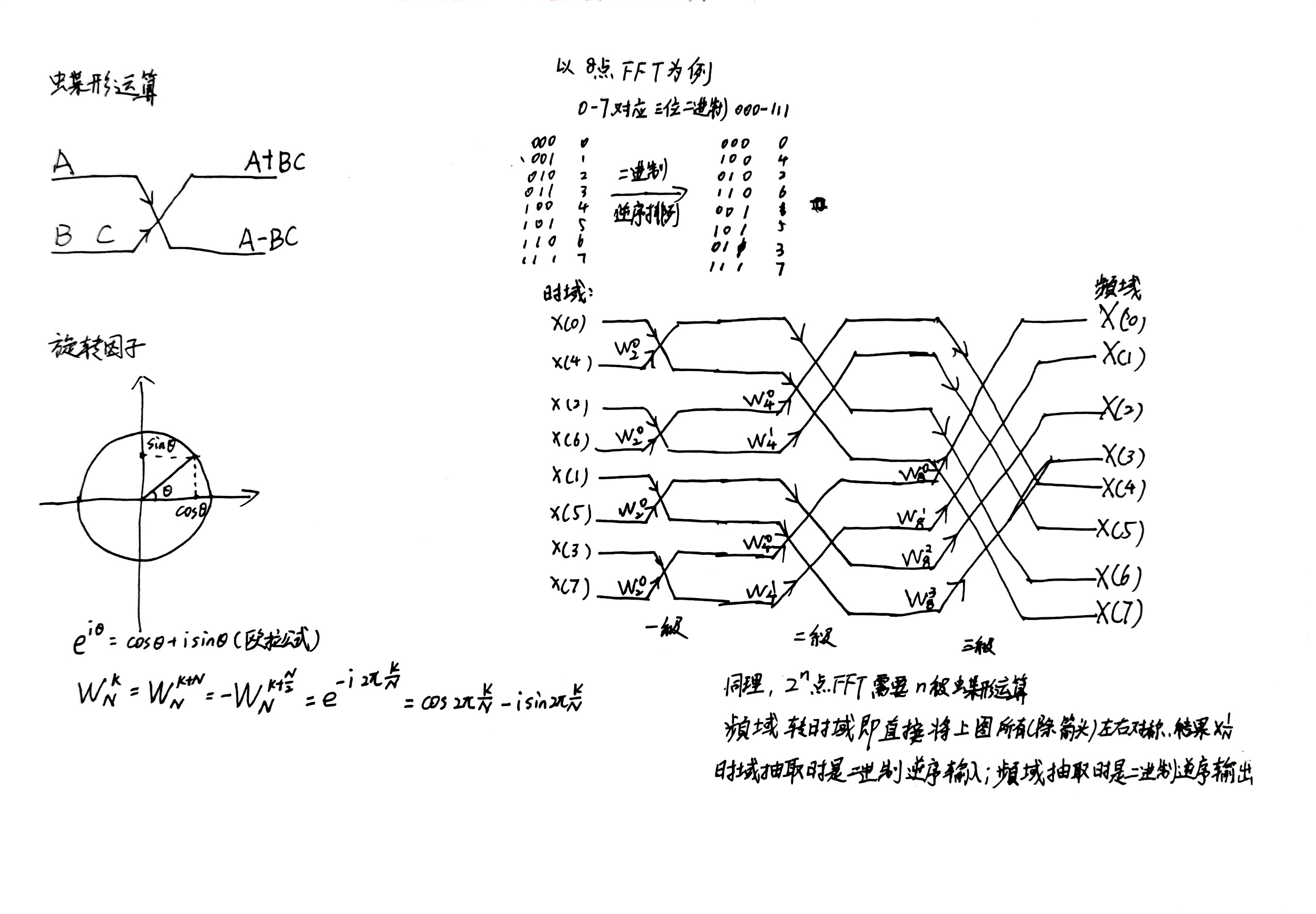
3.目的
本文的目的是学会配置FFT,并知道如何获取频谱数据,并利用频谱数据进行后续的操作。
二、配置FFT
在同样的IP Catalog中搜索FFT,双击跳出来的唯一的FFT选项,对其进行命名(不放图了,懒。与其说是懒,不如说拿出之前做对的来不会出错)。
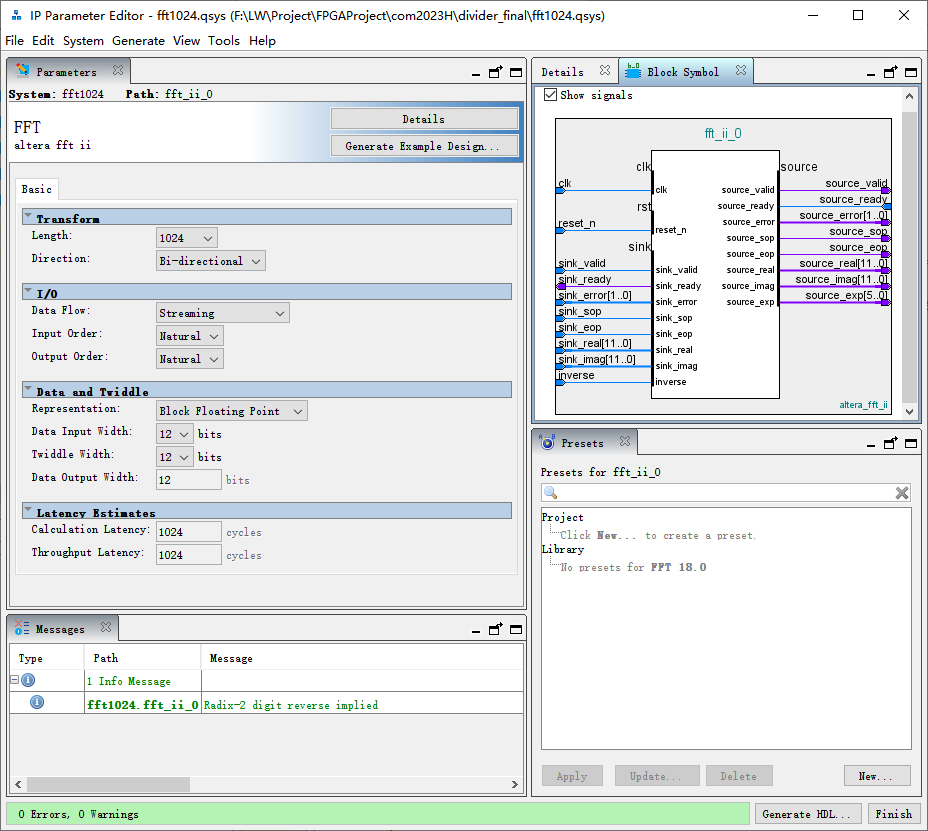
可以看到,FFT的IP配置界面相比于NCO和PLL的界面就比较整洁,我们还是从上到下的顺序来解读每个选项。
1.Transform
Transform(变换)这里我认为是对快速傅里叶变换(FFT)的简写,也就是对FFT本身进行配置。
Length(长度)这里的长度也就是数字信号处理里常说的N点FFT。这个N的大小与采样频率Fs和频率分辨率dF之间的关系是dF = Fs / N。由此不难看看出,N越大,FFT得到的频谱的频率分辨率越高;采样频率Fs越大,FFT得到的频谱的频率分辨率越低。由于现在通信频率的逐渐升高,为保证采样的完整性(假设奈奎斯特采样),Fs也一定越来越高,导致在需要相同的频谱频率分辨率的条件下,N也就需要的越大,即FFT的长度越长。之前的博客里有涉及到FPGA的资源问题,这里也有:FFT的长度越长,占用FFT的资源也就会越大。因此我们需要合理的选择FFT的长度,这里考虑到我的FPGA资源的问题,选用了1024点FFT。
Direction(方向)这里的方向指的是FFT的运算方向,即从时域变换到频域的正向FFT(Forward)、从频域变换到时域的FFT逆变换(Reverse)和正向反向的双向变换(Bi-directional)。这里我选择了双向变换。
2.I/O
Data Flow(数据流)代表选择需要FFT的模块芯片的数据输入方式,不同的数据输入方式自然也是应对各种方面的情况,包括具有高速性的Streaming(流水线)、具有低资源占用的Burst(爆发),中间的Variable Streaming(多种流水线)和Buffered Burst(缓冲爆发)分别居中,但前者更加贴近Streaming,后者更加贴近Buffered Burst。
由于我对内存的理解程度不够高,运用的自然就不是那么好,因此就选择最直接的流水线的输入方式。这种输入方式会占用较高的资源但是架不住它的运算速度是真的快,输入了一个周期的数据之后,下一个周期就能输出数据了。
选择了Streaming以后,后面的Input Order和Output Order(输入输出格式)就只能选择
Nature(自然数)了。
3.Data and Twiddle
Representation(表示)即数据的表示方式,Fixed Point(固定点)、Single Floating Point(单浮点)、Block Floating Point(块浮点)同样是各有优缺点。Fixed Point的资源消耗最低,无法动态小数点位置导致表示数值的大小存在溢出的风险;Single Floating Point是标准的浮点数的格式,每个数据都有自己独立的指数(权),因此资源相对占用较多;Block Floating Point在Single Floating Point上把独立指数(权)动态变成了一个公共的、仍能保证数据有效的值,属于Fixed Point和Single Floating Point的中间选项,也是大部分FFT模块芯片的配置选择。
Data Input Width(数据输入宽度)这个应该大家也都明白,代表着输入数据的位宽,位宽越宽,数据的精度就越高。Twiddle Width(旋转因子宽度)这个旋转因子就是我在上文手写的理论计算方法里的旋转因子,是一个模长等于1的复数,因此位宽越宽也同样代表了其值的精度。
三、实例化
对配置好的FFT模块芯片进行生成HDL工作(步骤与之前的相同,这里就不再描述了,可以看一下学习FPGA(七)里面的三、实例化的最开头部分),再确认一下模块芯片的引脚。
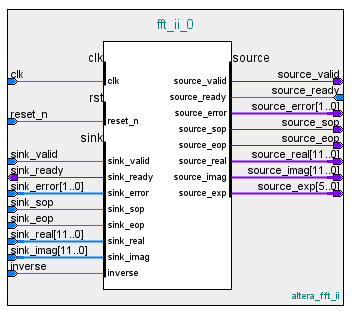
如上配置的FFT的实例化需要分成3个步骤,即前期的数据准备、芯片接入、后期数据处理。这里先讲芯片的接入,再将其前后的支持部分。
1.芯片接入
clk、reset_n就不说了,熟面孔,一个是时钟信号,一个是低电平复位信号。
左边最下面的inverse(反向)输入的0代表FFT正变换,1代表FFT逆变换。
sink_valid(信号的有效)这个自然是直接输入1(有些模块的信号输出存在暂时没准备好信号的正常输出,valid应输入0的可能)。
sink_ready(信号的准备)是芯片给外部发出可以输入信号的"准备好了"的信号。
sink_error(信号的错误)这个自然也是直接输入2'b00,高低位分别代表实部和虚部的信号是否正确。为什么不直接说高电平有效呢?有人会误解,以为高电平是有效的输入,其实是高电平代表这个引脚的功能生效,即数据错误,不进行运算。
sink_sop和sink_eop是输入信号的起始标识和结束标识一般二者间隔为设置的N点FFT的N倍时钟,高电平有效,如图,我画的应该就比较清晰了。
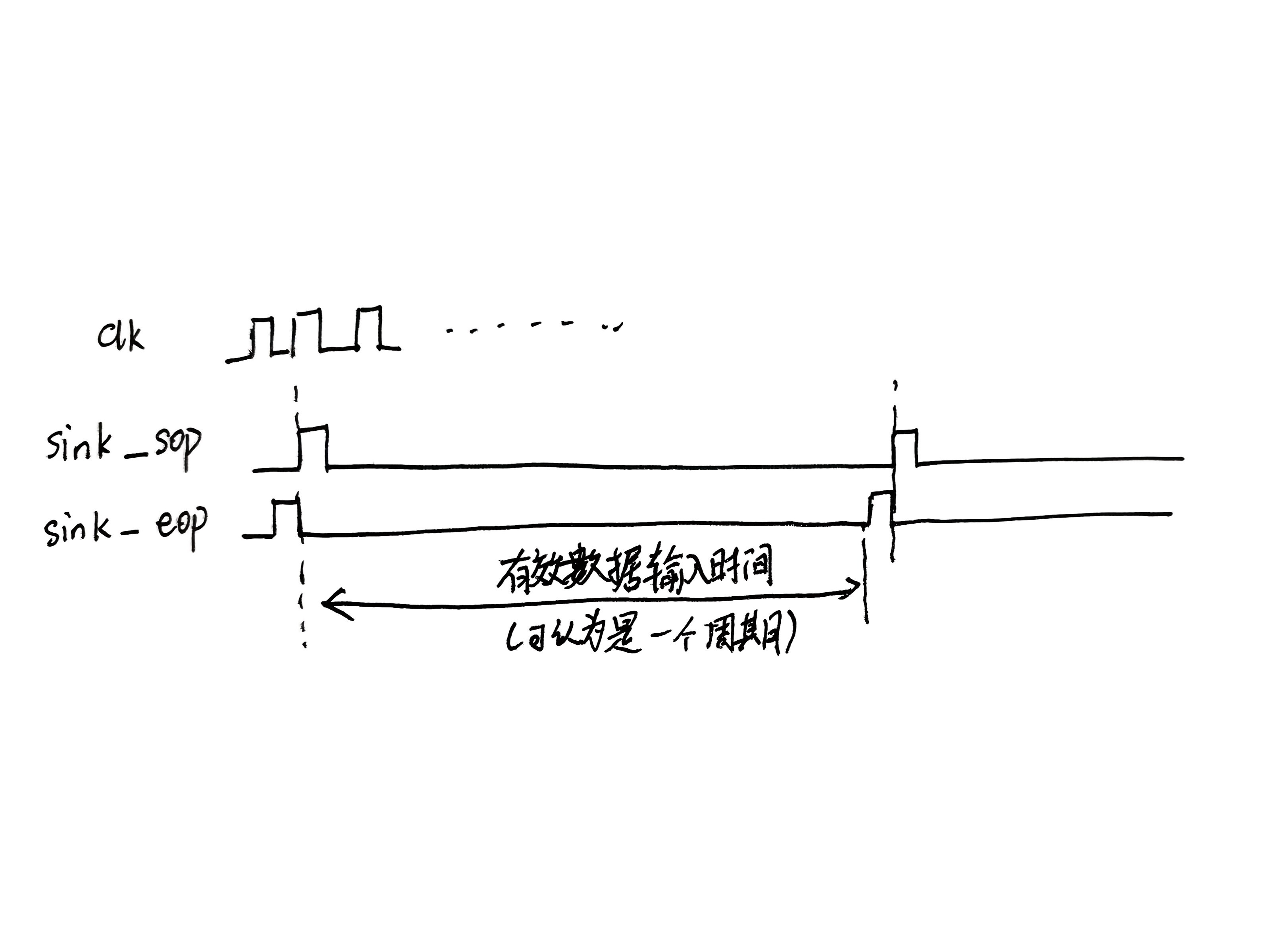
sink_real和sink_imag分别是输入信号的实部和虚部。如果是FFT正变换,那一般只有实部,信号采集的内容放在sink_real,sink_imag直接放入0。如果是FFT反变换,那么就分别放入实部和虚部。
除了source_exp(信号的指数)外,source_*与sink_*完全对称相反,就不多说了,输入换成输出、输出换成输入,功能相同。source_exp要配合着source_real和source_imag一起用,也就是前文我在Block Floating Point中说的,一个公共的、仍能保证数据有效的指数值。
2.数据准备
数据准备中,最重要的是起始符和结束符、输入信号要换成补码的和格式。
起始符的上升沿即代表数据开始输入了,结束符的上升沿代表数据结束输入。结束符在起始符的前一个时钟信号上升沿开始。这个留个心眼就行,如果能有仿真就更好了。
3.数据处理
获取了输出数据的实部、虚部、指数后,首先进行实部和虚部的补码换成原码,再能量谱的转换。
在输出数据有效的情况下,获取起始符和结束符,注意幅频特性线的对称性,只能取起始和截止的一半,及N点FFT只去频谱的前N/2部分,后半部分与前半部分完全对称。
4.代码实现
这里我就放中间截取的代码块了。
// 1024 pionts FFT and search peak
// Use 1024kHz sampling frequency, for the resolution frequancy will be about 1kHz
//// The two signal frequancy in the FFT will be saved in Var fft_out[0] and fft_out[1]
wire signed [11:0] Data_signed;
assign Data_signed = Din[11] ? Din - 12'h800 : Din + 12'h800; // 偏移至有符号范围(-2048~2047)
reg [9:0] sample_count; // 0~1023
always @(posedge clk1024k)
begin
if (sample_count == 10'd1023)
sample_count <= 0;
else
sample_count <= sample_count + 1;
end
// Gain FFT frame
wire sink_sop;
wire sink_eop;
assign sink_sop = (sample_count == 10'd0);
assign sink_eop = (sample_count == 10'd1023);
wire [11:0] real_out;
wire [11:0] imag_out;
wire source_valid;
wire freq_start;
wire freq_end;
wire [ 5:0] exp;
fft1024 u_fft (
.clk (clk1024k),
.reset_n (1),
.inverse (0),
.sink_valid (1),
.sink_sop (sink_sop),
.sink_eop (sink_eop),
.sink_real (Data_signed),
.sink_imag (12'b0),
.sink_error (2'b00),
.source_ready (1),
.source_valid (fft_valid),
.source_real (real_out),
.source_imag (imag_out),
.source_error (),
.source_sop (freq_start),
.source_eop (freq_end),
.source_exp (exp)
);
// Gain magnitude
wire [ 11:0] real_num;
wire [ 11:0] imag_num;
wire [ 23:0] power;
assign real_num = real_out[11] ? (~real_out + 1) : real_out;
assign imag_num = imag_out[11] ? (~imag_out + 1) : imag_out;
assign power = (real_num * real_num) + (imag_num * imag_num);
wire [11:0] magnitude_temp;
wire [17:0] magnitude;
sqrt u_sqrt(
.radical(power),
.q(magnitude_temp)
);
assign magnitude = magnitude_temp << exp;
// Get spectrum
reg [ 9:0] cnt;
reg freq_end_d;
always @(posedge clk1024k)
begin
if (freq_start) cnt <= 0;
else if (fft_valid) cnt <= cnt + 1;
if (fft_valid && cnt <= 10'd512)
begin
// magnitude即为当前频率下的幅频特性
end
end四、注意事项
先前配置操作的时候一直不知道哪里出错了,每次我输入数据的时候,都没能够得到预期结果,在分级调试后发现,问题常常出现在FFT的这个模块芯片上。现在回想起来,可能是数据输入模式上出现的问题,即在Data Flow的选择上出现了问题。之前说过,我对FPGA的内存的使用理解不是很深,除了Streaming的输入方式,其他的都或多或少要用到内存,导致了FFT的输出错乱。当然也不排除即便我使用了Streaming的输入方式,在起始标志和结束标志上的运算错误导致的FFT输出错乱的问题。
所以依我自己的看法:1.不太会使用内存的,建议使用Streaming;2.使用的Streaming的输入方式,起始标志和结束标志的需要仔细地推演(有仿真的话更好),不要出现标志符错位的现象。
总结
这里先感谢一下B站A_sail的视频给我的启发【基于FPGA的FFT开发-使用Quartus和Verilog的仿真设计流程】。当然我也见到过厉害的哥们直接通过原理自己写代码实现的FFT的功能,比如8点FFT设计(verilog);还有淘宝上也有前辈设计的FFT能买,但是自己写的存在的问题是消耗的资源太大,不足以满足实际的工程需求,但是如果想要自己结合一下理论进行实际的练习,自己写代码实现不失为一种很好的办法。如果是为满足工程需要,从我自己的角度,还是用系统的IP核配置一下更好。
再次说明一下以上博客的撰写是我自己根据自己对理论的理解、在实际操作中保留下来的正确的做法,存在小漏洞实属正常,遇到大问题请指出,谢谢!!