【Redis】Zset 有序集合

与集合不同的是，在member的基础上，引入了一个属性分数score,它是浮点类型，zset会给每一个member安排一个分数，即有序集合中的每个元素都有⼀个唯⼀的浮点类型的分数（score）与之关联 ，着使得有序集合中的元素是可以维护有序性的，但这个有序不是用下标作为排序依据而是⽤这个分数。

Zset中的member要保证是唯一的，score可以重复。主要还是来存储member的，score只不过是辅助作用。有序集合中的元素是不能重复的，但分数允许重复。类⽐于⼀次考试之后，每个⼈⼀定有⼀个唯⼀的分数，但分数允许相同。

🐼Zset命令

✅ZADD

添加或者更新指定的元素以及关联的分数到 zset 中,分数应该符合 double 类型，+inf/-inf 作为正负极限也是合法的。在添加的时候，既要添加分数，也要添加元素

时间复杂度：**O(log(N))，**因为要保证插入后元素还是有序的，底层用的跳表

返回值：本次添加成功的元素个数。注意，这里的返回值，并不算成功修改的元素，如果一个对一个已经存在的元素进行修改，返回值仍然为0,这里仅仅是新增

cpp 复制代码

ZADD key [NX | XX] [GT | LT] [CH] [INCR] score member [score member
...]

这里的score, member类似于我们在C嘎嘎中的pair,并不是键值对，没有明确的角色区分，谁是谁的键，谁是谁的值。我们既可以通过score找到member，也可以通过member找到score

💮选项

如果不带[NX | XX ]，也就是默认情况。根据redis文档，如果member不存在，那么就是添加新member,score的效果；如果member已经存在，那么就会更新member的score。
如果带上NX :那么只有当member不存在时，才会添加member，如果member已经存在了，不会更新，直接返回,带上NX,可以防止直接覆盖掉旧值，比较安全！
如果带上XX:那么只有当member存在，则会更新member的score；如果不存在，直接返回，如果想更新一个值，并且不新建，推荐带上XX。注意，NX和XX是相反的，只能选择其一
CH：默认情况下，ZADD 返回的是本次添加的元素个数，但指定这个选项之后，就会还包含本次更新的元素的个数,本来zdd返回的是新增元素的个数。也就是返回值算上更新的元素了。不然更新元素是返回0的
INCR：此时命令类似 ZINCRBY 的效果，将元素的分数加上指定的分数。此时只能指定⼀个元素和分数
LT：只有当新分数比原本分数还要小，才会更新，也就是越更新来越小。如果更新的值不存在，那么就会新建
GT：只有当新分数比原本分数还要大，才会更新，也就是越更新来越大。如果更新的值不存在，那么就会新建

🍃上面有几个问题，就是如果分数既然可以重复，但是member不能重复，如果分数重复了，怎么排序？如果分数重复了，那么就按照member的字典序排序。

🍃在redis官方文档说了，member默认是按照score的升序来排序的。

🍃假设我们现在插入了几组值：

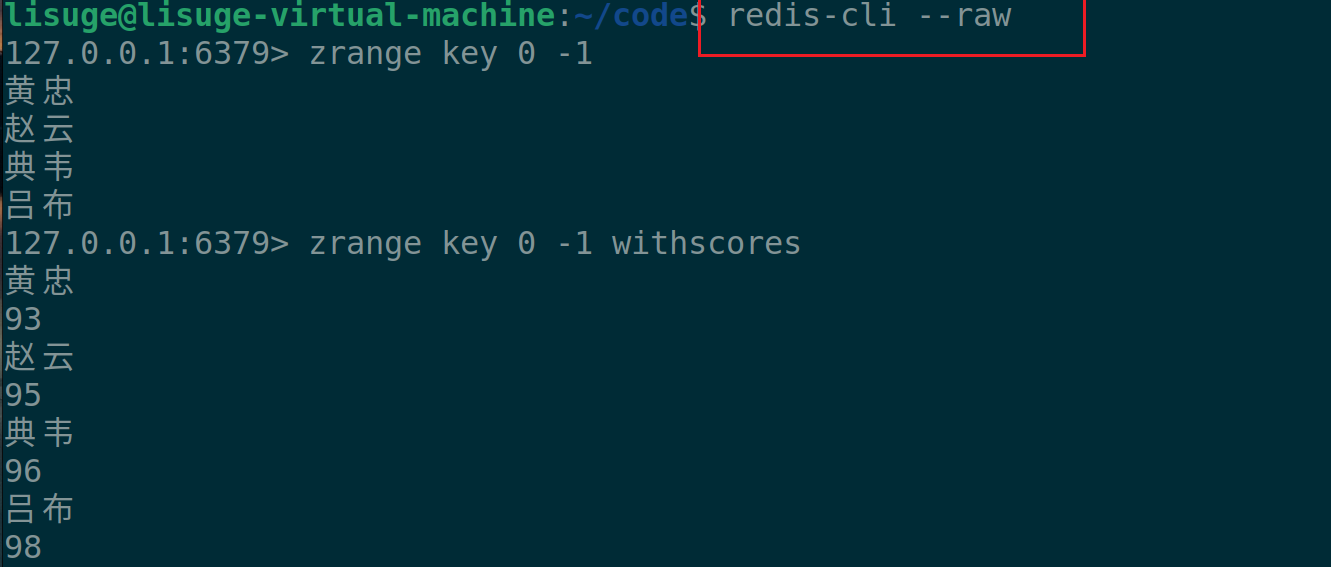
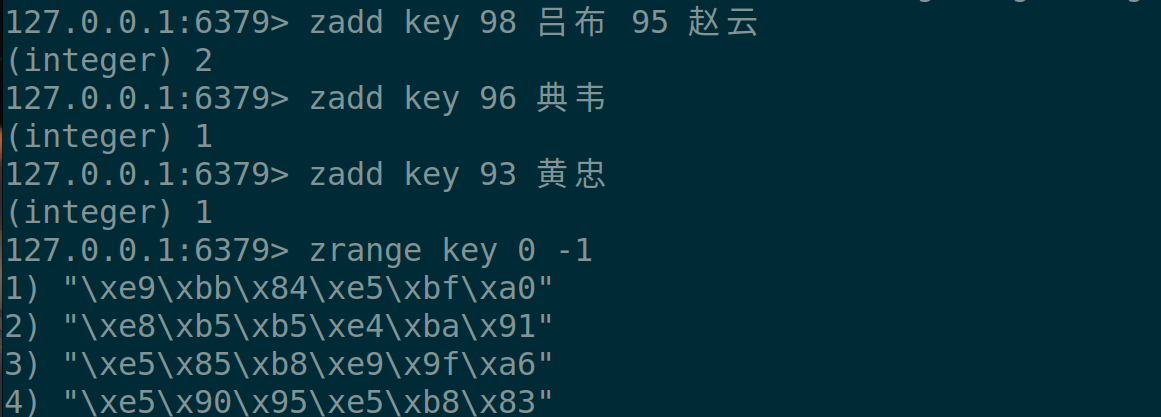但是我们发现并没有看到我们插入的汉字。这是为啥？之前说过了，首先redis是基于c-s的网络服务，我们发的请求都是交给redis服务器，而redis服务器由于考虑效率，并不做编码转换，那谁来做编码转换，redis客户端。因此，我们在启动redis-cli时，带上**--raw选项**

✅ZCARD

获取⼀个 zset 的基数（cardinality），即 zset 中的元素个数

cpp 复制代码

ZCARD key

时间复杂度：O(1)

返回值：zset 内的元素个数。

✅ZCOUNT

返回分数在 min 和 max 之间的元素个数，默认情况下，min 和 max 都是包含的，可以通过 **(**排除

cpp 复制代码

ZCOUNT key min max

如果既要排除min,又要排除max可以这么写

cpp 复制代码

ZCOUNT key (min (max

时间复杂度：O(log(N))，只需要找到两个端点值即可

返回值：满⾜条件的元素列表个数。

支持浮点数两个特殊的数值：负无穷大和无穷大：-INF 到 INF

✅ZRANGE

返回指定区间⾥的元素，分数按照升序。带上 WITHSCORES 可以把分数也返回

cpp 复制代码

ZRANGE key start stop [WITHSCORES]

此处的 [start, stop] 为下标构成的区间. 从 0 开始, ⽀持负数.[0, -1] 即可获取所有元素

命令有效版本：1.2.0 之后时间复杂度：O(log(N)+M)为什么是O(logN + M),查找到start下标是O(LogN),然后遍历一一取出M个元素

返回值：区间内的元素列表

✅ZREVRANGE

返回指定区间⾥的元素，分数按照降序。带上 WITHSCORES 可以把分数也返回

注意：这个命令可能在 6.2.0 之后废弃，并且功能合并到 ZRANGE 中。

cpp 复制代码

ZREVRANGE key start stop [WITHSCORES]

时间复杂度：O(log(N)+M) 返回值：区间内的元素列表。

🌞来谈一谈兼容性，为什么之前一些设计不好的东西，不能轻易改掉？因为一款广泛应用的软件，一旦想增加新版本，引入和之前不兼容的特性是非常难的，我们使用者不愿意！因为我们已经将旧版本部署应用到我们服务器上了。这就是IPV6推广慢，和IPV4不兼容的原因，当然也有兼容的案例，比如C++就兼容C语言。所以不仅针对zrevrange,想zrange 设计开区间那么设计，后面改就很难了~

✅ZRANGEBYSCORE

返回分数在 min 和 max 之间的元素，默认情况下，min 和 max 都是包含的，可以通过 ( 排除。备注：这个命令可能在 6.2.0 之后废弃，并且功能合并到 ZRANGE 中。

zount 仅仅只能获取min max的元素个数，但是这个能获取到元素个数的元素列表

zrange和zrevrange是按照下标来取一段区间的，zrangebyscore是按照分数来取一段区间的

cpp 复制代码

ZRANGEBYSCORE key min max [WITHSCORES]

时间复杂度：O(log(N)+M) 返回值：区间内的元素列表。

✅ZPOPMAX

删除并返回分数最⾼的 count 个元素

cpp 复制代码

ZPOPMAX key [count]

时间复杂度：O(log(N) * M)

返回值：分数和元素列表

注意：如果有多个分数相同的元素，同时为最大值，那么zpopmax删除的时候，也只会删除一个元素，即删除这些同时分数相同但member字典序最大的元素

🔎思考一下这里的时间复杂度为什么是O(logN * M)

这里删除的元素有点特殊，删除的是最大的元素，即尾删。可是尾删一个元素，不是有一个下标可以做到吗，如果直接通过最后一个下标，然后删除这个元素，那么单次删除的时间复杂度完全可以是O（1），之后删除次大的元素，就是前一个下标，然后删除M次，时间复杂度为O(M)，对吧？

是的！但是很遗憾，redis并没有这么做。在redis源码中确实记录了尾部这样的特殊位置。

但是在实际删除元素时，没有利用删这个特性，统一调用的删除操作（即根据score找到位置然后删除），导致每一次删除的时间复杂度为O(logN)。

既然能优化，为什么redis没有优化，因为这个删除操作可能不是性能瓶颈点！什么是性能瓶颈点：即同样干一件事情，分为好多个步骤，在花费时间较少的事情上你使劲优化，没啥用~往往在花费时间较长的事情上优化才有用！而这个花费时间占比较重的步骤，就是性能瓶颈点~跟追妹子一样

✅BZPOPMAX

同我们之前学习的阻塞版本的blpop思想同理，这是zpopmax的阻塞版本。

即在有序集合为空的时候触发阻塞，一直阻塞到有其他客户端插入元素

cpp 复制代码

BZPOPMAX key [key ...] timeout

时间复杂度：O(log(N))

返回值：元素列表

🔎来思考一个问题，假设现在bzpopmax同时检测了m个key，那么时间复杂度是？

O(LogN),因为只需要查找到一个key，删除一次即可，并没有删除M次，而zpopmax会删除m次，不像bzpopmax检测到一个key有数据删除一次就立即返回

✅ZPOPMIN

删除并返回分数最低的 count 个元素

时间复杂度：O(log(N) * M) 返回值：分数和元素列表

同zpopmax

cpp 复制代码

ZPOPMIN key [count]

✅BZPOPMIN

ZPOPMIN 的阻塞版本。

时间复杂度：O(log(N)) 返回值：元素列表

cpp 复制代码

BZPOPMIN key [key ...] timeout

通过zpopmax/zpopmin实现了类似优先级队列的效果！

✅ZRANK

返回指定元素的排名，升序。

时间复杂度：O(log(N)) 返回值：排名，就是下标，所处在zset的位置

cpp 复制代码

 ZRANK key member

✅ZREVRANK

返回指定元素的排名，降序

时间复杂度：O(log(N)) 返回值：排名

cpp 复制代码

ZREVRANK key member

✅ZSCORE

返回指定元素的分数

cpp 复制代码

ZSCORE key member

时间复杂度：O(1)，重要！

返回值：分数

🔎这里的时间复杂度为什么是O(1)呢，前面不都是要先找到member，再删除吗，时间复杂度为O(logN)，这里不应该一样吗？是的！但是redis根据这样的查询操作做了优化，付出了额外的空间代价，将时间复杂度优化为了O(1)实现。

✅ZREM

删除指定的元素

cpp 复制代码

ZREM key member [member ...]

时间复杂度：O(M*log(N))

返回值：本次操作删除的元素个数，成功删除几个就返回几！

✅ZREMRANGEBYRANK

按照排序，升序删除指定范围的元素，左闭右闭

cpp 复制代码

ZREMRANGEBYRANK key start stop

时间复杂度：O(log(N)+M)

返回值：本次操作删除的元素个数

🔎这里的时间复杂度为什么是O(logN+M)呢,前面不都是O(LogN*M)，因为此处查找操作，只需要操作一次，然后删除key-start的M个元素即可

✅ZREMRANGEBYSCORE

按照分数删除指定范围的元素，左闭右闭

bash 复制代码

ZREMRANGEBYSCORE key min max

时间复杂度：O(log(N)+M)

返回值：本次操作删除的元素个数

✅ZINCRBY

为指定的元素的关联分数添加指定的分数值

increment可以为分数也可以为小数，因为score本身就是double

cpp 复制代码

ZINCRBY key increment member

时间复杂度：O(log(N))

返回值：增加后元素的分数

不光会修改分数内容，同时会移动分数位置，仍然确保zset是有序的

总结一下，正是因为Zset是一个有序集合，才会多了那么多比Set的操作，比如根据范围(下标)或者根据分数/member的操作。并且要理解zset中的kv不是键值对，可以根据分数可以获取到member(比如zrangebyscore, zremrangebyscore...),也根据member也可以获取到分数(zrank...)

至于具体的时间复杂度，理解，如果还不确定，可以翻阅一下redis官网文档，毕竟学着看英文文档，是咱程序员的必备技能

🐼集合间操作

既然Zset是集合，那么当然也有关于集合的操作了，交集并集差集，比如set的sinter,sunion,sdiff

可是不幸的是，关于Zset的zinter,zunion,zdiff这几个命令是在Redis6.2之后才支持的。

比如zdiff的语法：

bash 复制代码

ZDIFF numkeys key [key ...] [WITHSCORES]

这跟sdiff类似，只不过多了一个numkeys，这里的numkeys是为了区分出有多少个key,和后面的选项分离开的，对于zinter,zunion可以翻阅文档

我们这里先介绍redis6.2之前能够支持的操作

✅ZINTERSTORE

求出给定有序集合中元素的交集并保存进目标有序集合 中，在合并过程中以元素为单位进⾏合并，元素对应的分数按照不同的聚合⽅式和权重得到新的分数

cpp 复制代码

ZINTERSTORE destination numkeys key [key ...] [WEIGHTS weight
[weight ...]] [AGGREGATE <SUM | MIN | MAX>]

我们来一一看看这些参数的意思：

其中destination就是合并后的目标有序集合
numkeys表示我们需要操作几个key的有序集合。这里为什么要单独指出key的个数，之前学的zadd 或者 mget mset有没有指定啊。原因是key后面可能还带参数，指定key的个数是为了将key和后面的选项分离开，有点类似于协议如何将报文和有效载荷分离开类似。
weights表示每个key你指定的权重，比如key1指定0.2,key2指定0.3,key3指定0.4 ... 支持小数，也支持分数，如果你要指定权重，带上WEIGHTS
AGREEGATE是总数的意思，其中有三种形式，如果是sum,那么就是每个key对应的score相加后再为des目标member的score,如果是min,那么就是求所有key的最小score,如果是max,那么就是求所有key的最大score作为目标key的score。如果你要指定求和方式，带上AGGREGATE

这里需要注意的是，假设我们求交集，如果member相同，但是分数不同，那么他们算相同吗？

算！在比较相同的时候，只需要保证member相同即可，score相不相同不重要了，可以这么理解，在有序集合zset中，member才是主体，score只是起辅助作用。

时间复杂度：O(N*K)+O(M*log(M)) N 是输入的有序集合中, 最小的有序集合的元素个数; K 是输⼊了⼏个有序集合; M 是最终结果的有序集合的元素个数，怎么来的？只能参考源码了

返回值：⽬标集合中的元素个数

注意，如果什么选项都不带，默认AGREEGATE是求和操作

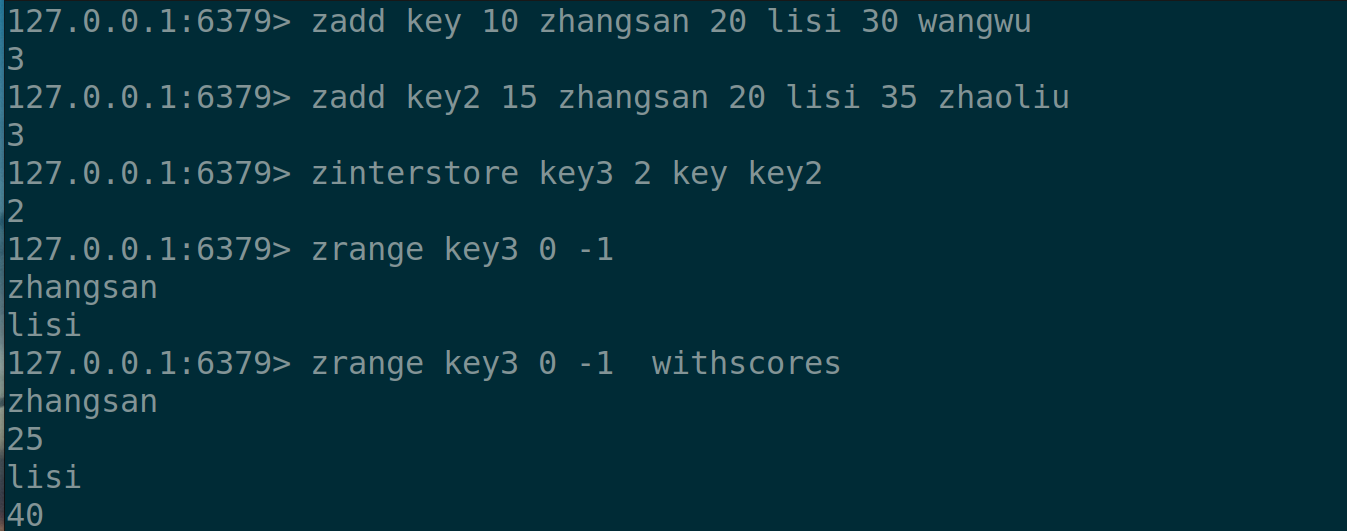
✅ZUNIONSTORE

同ZINTERSTORE,只是这里求并集操作了，选项都是一致的。

求出给定有序集合中元素的并集并保存进⽬标有序集合中，在合并过程中以元素为单位进⾏合并，元素对应的分数按照不同的聚合⽅式和权重得到新的分数

bash 复制代码

ZUNIONSTORE destination numkeys key [key ...] [WEIGHTS weight
[weight ...]] [AGGREGATE <SUM | MIN | MAX>]

时间复杂度：O(N)+O(M*log(M)) N 是输⼊的有序集合总的元素个数; M 是最终结果的有序集合的元素个数.

返回值：目标集合中的元素个数

以上命令也不需要可以去记，理解会用，需要查文档即可。用多了自然就会了~

这里也有个小技巧，在输入完小写的关键字后，tab就能立马将小写转换为大写

🐼Zset的内部编码

有序集合类型的内部编码有两种

当元素个数较小并且单个元素的大小不大时，zset会采取ziplist的方式来存储，节省内存空间

当元素个数较多或者单个元素的大小超过了一定的大小时，zset会采取skiplist(跳表）的方式来存储。跳表就是一个"复杂的链表"，相比与AVL树红黑树等，跳表的查询速率不仅仅是O(LogN),并且跳表更擅长范围查找，这就是为什么我们上面很多的操作都是带range的，进行范围查找

🐼Zset的使用场景

Zset最关键的使用场景：作为排行榜系统，比如游戏的排行榜，微博的热搜等...这些分数实时变化的，都可以使用Zset。

🍓比如游戏排行榜

将玩家的信息(member)和分数(score)存入有序集合中，就自动形成了一个排行榜。随时可以根据下标，按照分数，按照玩家信息(member)进行查询。

并且随着分数的改变，比如玩家刚打完一把游戏上分/掉分，都可以实时更新，使用zincrby进行更新分数，顺便调整排行榜系统，我们可以使用zrevrange key 0 100 withscores

来查看天梯榜排行前100的选手

🚩可是有个问题就是，那么多玩家信息，我一个Zset能存下吗？这个存是redis-server在内存中存的

假设现在有一亿个玩家！

如果我们记录一个玩家的信息，member:userid ,4个字节 42亿九千万，足够记录玩家信息了

score : 玩家分数 8个字节，够表示一个玩家的打的分数了。

那么我们Zset存放一个玩家的完整信息才12字节，1亿个玩家也就大概1.2G大小（t,m,b）。

这里有个小tips:就是10^3(千) 10^6（百万） 10^9(10亿) 和计算机中的kb, mb, gb大概是相等的，

所以1亿玩家占得大小为10^8 * 10 = 10^9 约为 1.2G

这对于计算机微不足道~

🍓微博热搜

对于游戏，只需要存储游戏的分数就够了。可是对于微博热搜这种，考虑的东西比较多，比如评论数，点赞数，视频播放量，转发量...

那有了这些因素，还如何计算热度呢？Zset怎么存呢？

我们是不是可以给每一个因素分配一个Zset,比如评论数，有一个Zset：<同一个微博ID，评论数>

；点赞数，有一个Zset：<同一个微博ID，点赞数>；视频播放量数，有一个Zset：<同一个微博ID，视频播放量数>；转发量，有一个Zset：<同一个微博ID，转发量>...

那么计算热度的时候，我们就可以综合的给每一个因素分配权重了，然后利用Zset求交集借助zinterstore,zunionstore 等这样的操作，分配权重这样的操作计算热度了，至于如何分配权重，可以根据大模型来提取特征来精准计算了。这样，通过不同的维度进行计算，得到的分数就是热度了！

当然Zset的使用场景不值这些，在使用时如果需要利用有序集合这样的特点，首选Zset,但是如果不在redis中开发，又要使用有序集合这样的特点呢？那我们看能不能引入一些现有的库，或者我们手搓一个类似redisZset使用跳表搓出来嘛！