一、图的基本概念
图是由顶点集合及顶点间的关系组成的一种数据结构:G=(V,E),其中:顶点集合V={x|x属于某个数据对象集}是有穷非空集合。
E={(x,y)|x,y属于V}或者E={<x,y>|x,y属于V&&Path(x,y)}是顶点间关系的有穷集合,也叫做边的集合。
(x,y)为双向通路,Path(x,y)表示x到y的一条单向通路,即有向的。
顶点和边:图中结点称为顶点,第i个顶点记作vi。两个顶点vi和vj相关联称作两点有一条边。
有向图和无向图:在有向图中,顶点对<x,y>是有序的,顶点对<x,y>称为顶点x到顶点y的一条边,<x,y>和<y,x>是两条不同的边
完全图:即该图每个顶点都与其余顶点直接相连。
邻接顶点:无向图中,两点直接相连,则称两点互为邻接顶点。在有向图中,若<u,v>是E(G)中的一条边,则称顶点u邻接到v,顶点v邻接自顶点u,并且称边<u,v>与顶点u,v相关联。
顶点的度:顶点v的度是指与它相关联的边的条数,记作deg(v)。在有向图中,顶点的度等于该顶点的入度和出度之和,其中入度是以v为终点的有向边的条数,记作indev(v);顶点v的出度是以v为起点的有向边的条数,记作outdev(v)。
路径:在图G=(V,E)中,若从顶点出发vi有一组边可以使其到达vj则称为vi到vj的顶点序列为顶点vi到顶点vj的路径。
路径长度:对于不带权值的图,一条路径的路径长度是指该路径是的边的条数;对于带权的图,一条路径的路径长度是指该路径上各个边权值的总和。
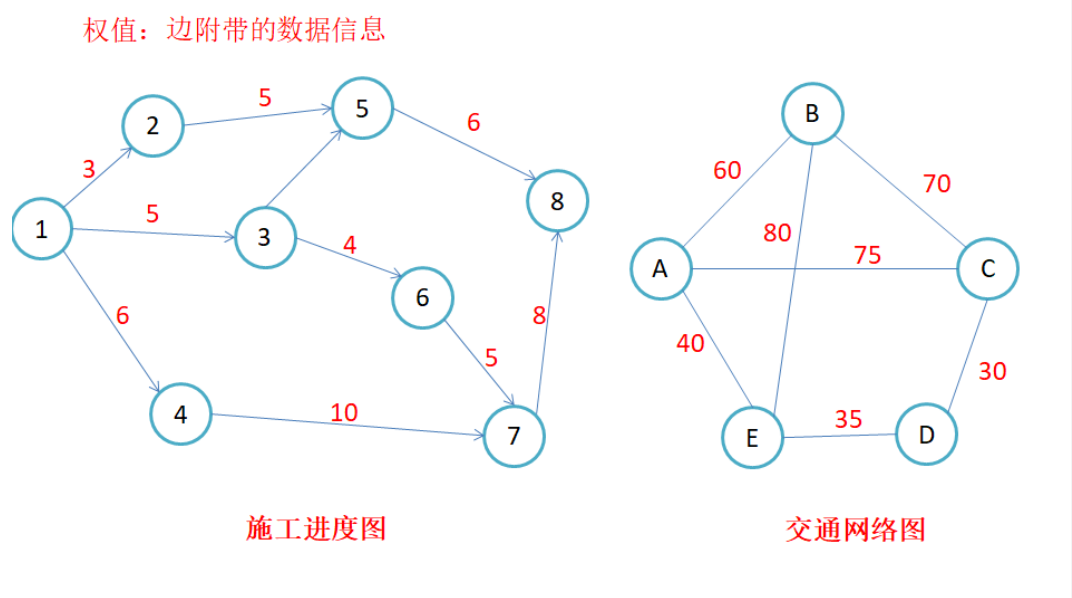
简单路径与回路:若路径上各个顶点v1,v2,v3......vm均不重复,则称这样的路径为简单路径。若路径上的第一个顶点v1和最后一个顶点vm重合,则称这样的路径为回路或者环。
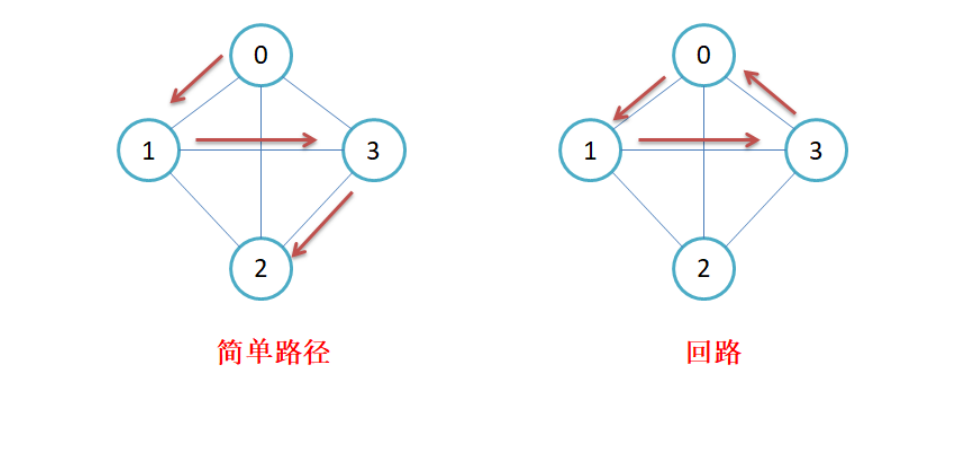
子图:设图G={V,E}和图G1={V1,E1},若v1属于V且E1属于E,则称G1是G的子图。
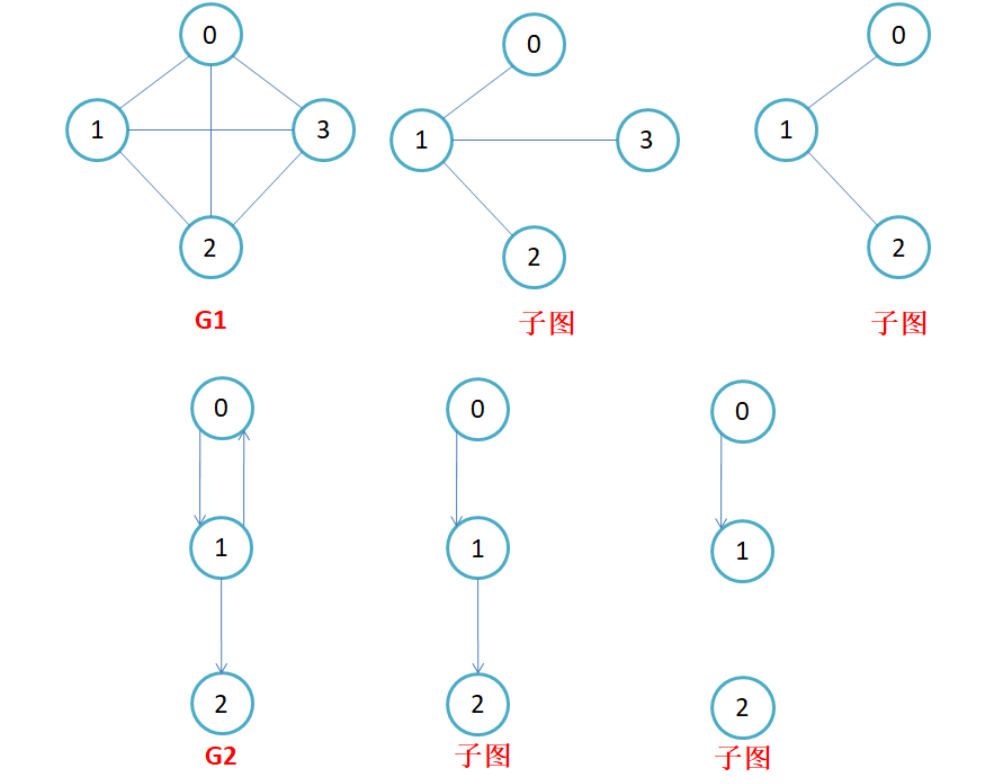
连通图:在无向图中,若从顶点v1到顶点v2有路径,则称v1,v2是连同的。如果图中任意一对顶点都是连同的,则称此图为连通图。
强连通图:在有向图中,若在每一对顶点vi和vj之间都存在一条从vi到vj的路径,也存在一条从vj到vi的路径,则称此图为强连通图
生成树:一个连通图的作息连通子图称作该图的生成树。有n个顶点的连通图的生成树有n个顶点和n-1条边。
二、图的存储结构
因为图中既有结点,又有边(结点和结点之间的关系),因此在图的存储中,只需要保存:结点和边关系就好。结点保存比较简单,只需要一段连续空间即可,那边关系该如何保存呢?
1.邻接矩阵
因为结点与结点之间的关系就是连通与否,即为0或者1,因此邻接矩阵(二维数组)即是:先用一个数组将定点保存,然后采用矩阵来表示结点和结点的关系。
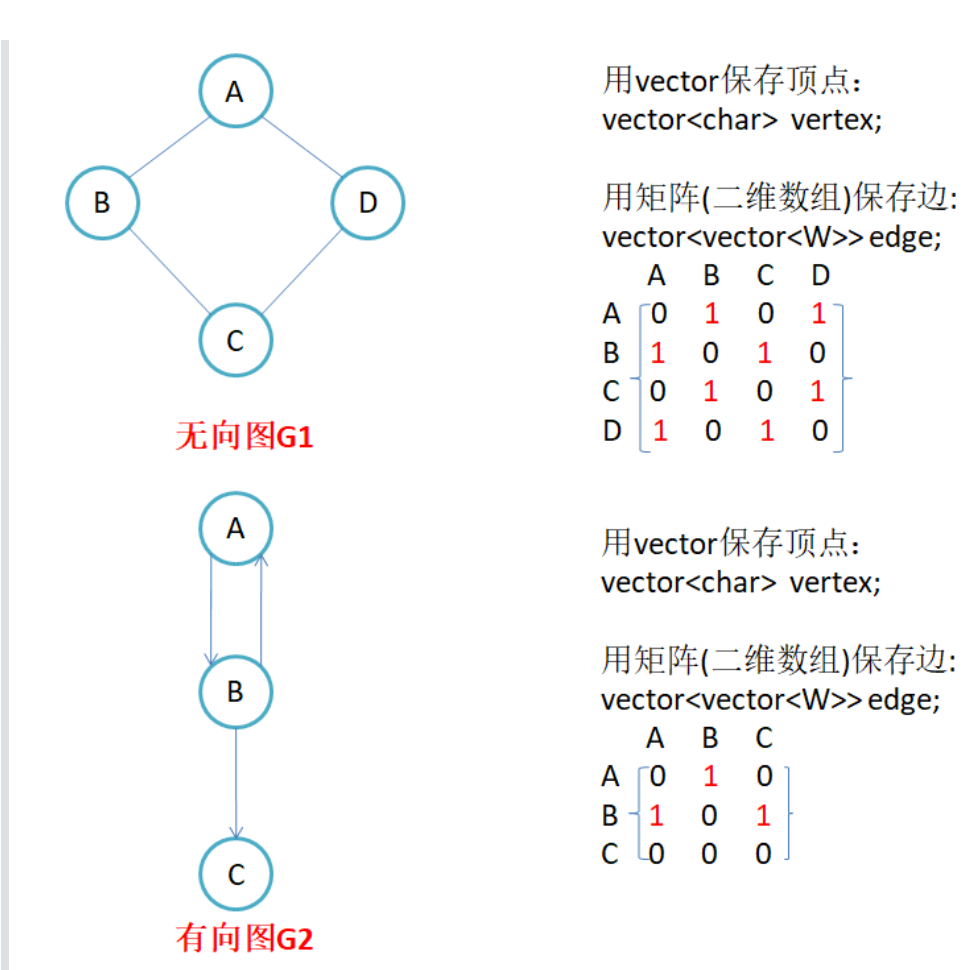
注意:
1.无向图的邻接矩阵是对称的,第i行(列)元素之和,就是顶点i的度。有向图的邻接矩阵则不一定是对称的,第i行(列)元素之和就是顶点i的出(入)度。
2.如果边带有权值,并且两个结点是连通的,上面图中的边的关系就用权值替代,如果两个顶点不通,就用无穷大来替代。
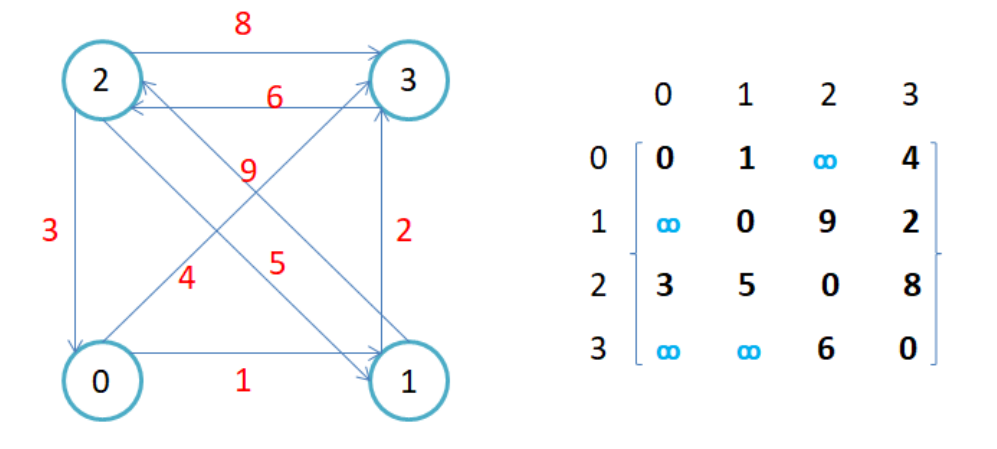
3.用邻接矩阵存储图的优点是能够快速知道两个顶点是否连同,缺陷是如果顶点较多,边比较少的时候,矩阵中存储了大量为0的系数矩阵,比较浪费空间,并且要求两个结点之间的路径不是很好求。
cpp
struct Edge {//定义边
int _scri;
int _dest;
W _w;
Edge(int scri, int dest, const W& w)
:_scri(scri)
, _dest(dest)
, _w(w)
{}
};
cpp
template<class V, class W, W MAX_W, bool Direction = true>
class Graph {
public:
typedef Graph<V, W, MAX_W, Direction> self;
typedef Edge<W> Edge;
Graph() = default;//系统生成默认构造
Graph(const V* vertexs, size_t n) {
_vertexs.reserve(n);
for (int i = 0; i < n; i++) {
_vertexs.push_back(vertexs[i]);
_vIndexMap[_vertexs[i]] = i;
}
//初始化邻接矩阵
_matrix.resize(n);
for (int i = 0; i < n; i++) {
_matrix[i].resize(n, MAX_W);
}
}
size_t GetVertexIndex(const V& v) {
size_t count = _vIndexMap.count(v);//判断map里是否有该元素
if (count == 0) {//无
return -1;
}
else {//有
return _vIndexMap[v];
}
}
void _AddEdge(size_t scri, size_t dest, const W& w) {
if (Direction == false&&scri>=dest) {
_matrix[scri][dest] = w;//对于无向图而言
_matrix[dest][scri] = w;//一次便将其赋值,避免两次调用
}
else {
_matrix[scri][dest] = w;
}
}
//这里要注意,上一个函数是给结点的下标,该函数是给结点的值
void AddEdge(const V& scri, const V& dest, const W& w) {
if (Direction == false ) {
_matrix[GetVertexIndex(scri)][GetVertexIndex(dest)] = w;
_matrix[GetVertexIndex(dest)][GetVertexIndex(scri)] = w;
}
else {
_matrix[GetVertexIndex(scri)][GetVertexIndex(dest)] = w;
}
}
void Print() {//打印矩阵,这里将没有通路打印成*
for (int i = 0; i < _matrix.size(); i++) {
for (int j = 0; j < _matrix.size(); j++) {
if (_matrix[i][j] != MAX_W)
cout << _matrix[i][j] << " ";
else {
cout << "*" << " ";
}
}
cout << endl;
}
}
void EdgePrint() {
for (int i = 0; i < _matrix.size(); i++) {
for (int j = 0; j < _matrix.size(); j++) {
if (_matrix[i][j] == MAX_W) {
continue;
}
else {
cout << _vertexs[i] << ":" << _vertexs[j] << " ";
}
}
cout << endl;
}
}
private:
map<V, size_t> _vIndexMap;
vector<V> _vertexs;//顶点集合
vector<vector<W>> _matrix;//邻接矩阵
};测试用例如下
cpp
void test01() {
Graph<char, int, MAX_W> g("0123",4);
g.AddEdge('0', '1', 1);
g.AddEdge('0', '3', 4);
g.AddEdge('1', '3', 2);
g.AddEdge('1', '2', 9);
g.AddEdge('2', '3', 8);
g.AddEdge('2', '1', 5);
g.AddEdge('2', '0', 3);
g.AddEdge('3', '2', 6);
g.Print();
g.EdgePrint();
}2.邻接表
邻接表:使用数组表示顶点的集合,使用链表表示边的关系
2.1无向图的邻接表存储
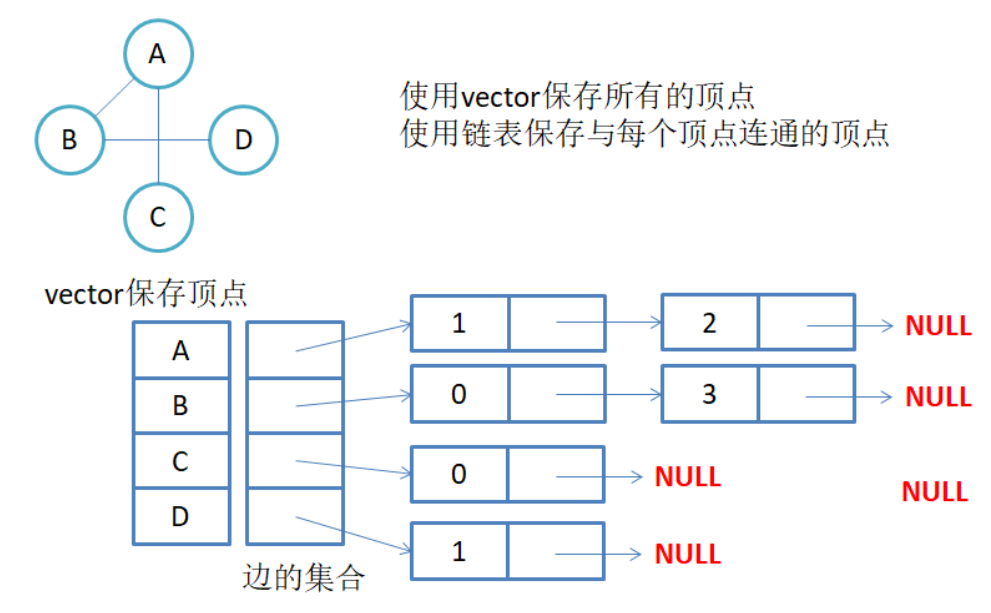
注意:无向图中同一条边在邻接表中出现了两次,如果想知道顶点vi的度,只需要知道顶点vi边链表中的结点个数就OK。
2.2 有向图邻接表存储
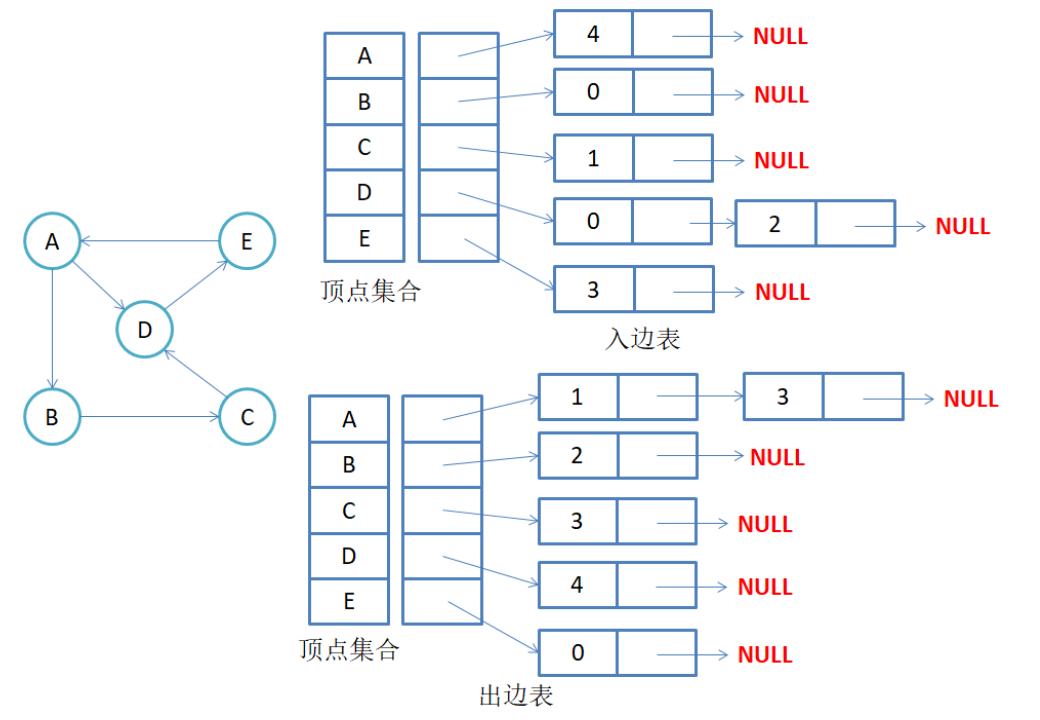
注意:有向图中每条边在领接表中只出现一次,与顶点vi对应的领接表所含结点的个数,就是该顶点的出度,也称出度表,要是得到vi顶点的入度,则需要遍历所有的结点的邻接表。
cpp
namespace LinkTable {
template<class W>
struct LinkEdge {//邻接表结点
int _scri;
int _dest;
W _w;
LinkEdge<W>* _next;
LinkEdge(const W& w)
:_scri(-1)
, _dest(-1)
, _w(w)
, _next(nullptr) {
}
};
template<class V, class W, bool Direction = false>
class Graph {
public:
typedef Graph<V, W, Direction> self;
typedef LinkEdge<W> LinkEdge;
Graph() = default;
Graph(const V* vertexs, size_t n) {
_linkTable.resize(n, nullptr);
_vertexs.reserve(n);//开辟n个空间给顶点集
for (size_t i = 0; i < n; i++) {
_vertexs.push_back(vertexs[i]);//将顶点依次插入顶点集
AddVertex(vertexs[i]);//添加顶点
}
}
int VertexFind(const V& v) {
if (_vIndexMap.count(v) != 0) {
return _vIndexMap[v];
}
else {
return -1;
}
}
bool AddVertex(const V& v) {//添加顶点的函数
if (VertexFind(v) != -1) {
return false;
}
else {
_vIndexMap[v] = _linkTable.size() - 1;
_linkTable.push_back(nullptr);
_vertexs.push_back(v);
}
}
void AddEdge(const V& scri, const V& dest, const W& w) {
size_t s = VertexFind(scri);//将顶点内容转化为下标
size_t d = VertexFind(dest);
if (s == -1 || d == -1) {//如果发现有顶点不存在
throw("没有这个顶点");
}
LinkEdge* l = new LinkEdge(w);
l->_dest = d;
l->_scri = s;
l->_next = _linkTable[s];
_linkTable[s] = l;
cout << scri << ":" << w << ":" << dest << endl;
if (Direction == false) {//无向图的情况
LinkEdge* _l = new LinkEdge(w);
_l->_dest = d;
_l->_scri = s;
_l->_next = _linkTable[s];
_linkTable[s] = l;
cout << dest << ":" << w << ":" << scri << endl;
}
cout << endl;
}
private:
vector<LinkEdge*> _linkTable;//边集合的邻接表
map<V, size_t> _vIndexMap;
vector<V> _vertexs;//顶点集合
};
}测试用例如下
cpp
void test02() {
string a[] = { "张三", "李四", "王五", "赵六" };
LinkTable::Graph<string,int,false> g1(a,4);
g1.AddEdge("张三", "李四", 100);
g1.AddEdge("张三", "王五", 200);
g1.AddEdge("王五", "赵六", 30);
g1.AddVertex("钱七");
g1.AddEdge("张三", "钱七", 10);
}三、图的遍历
给定一个图G和其中任意一个顶点v0,从v0出发,沿着图中各边访问图中所有的顶点,且每个顶点仅仅被遍历一次。"遍历"即是对结点进行某种操作的意思。
3.1图的广度优先遍历

也就是说我们会一层一层的去找 如图:
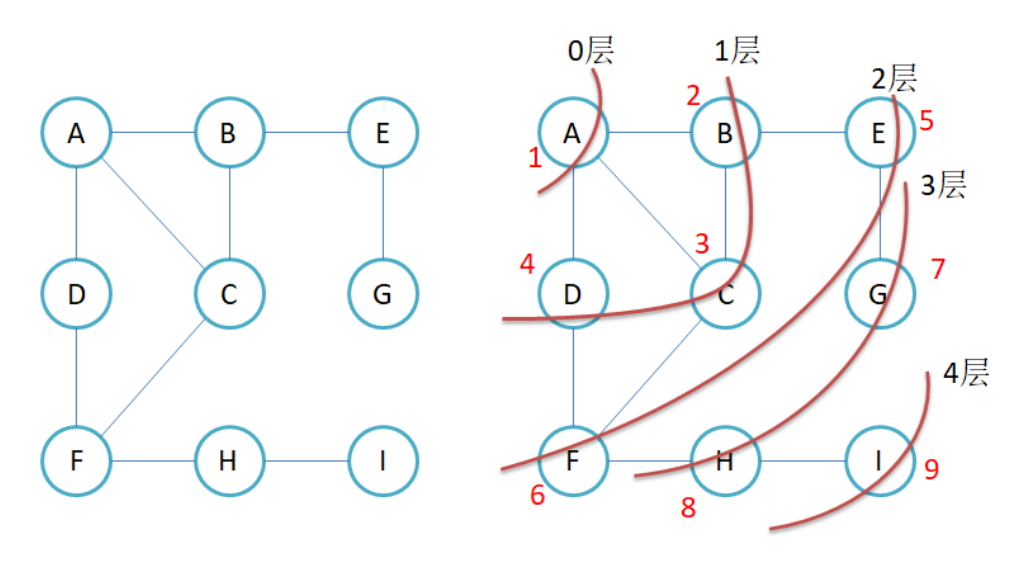
其主要问题是:如何防止结点被重复遍历
cpp
void BFS(const V& srci) {
int _vIndex = GetVertexIndex(srci);
queue<int> q;//定义一个栈来储存结点的下标
q.push(_vIndex);
vector<int> v;//定义vector来标记已经访问过的顶点
v.resize(_vertexs.size(), 0);
v[q.front()] = 1;
while (!q.empty()) {
int count = q.size();
//一次while循环相当于一层遍历
while (count > 0) {
//将其所有的路径全部判断一下
for (int i = 0; i < _vertexs.size(); i++) {
//遍历结点首先得有路径,其次要未遍历过
if (_matrix[_vIndex][i] != MAX_W && v[i] == 0) {
//如果有,将指向的结点入栈
q.push(i);
//并将指向的结点标记为已遍历
v[i] = 1;
cout << _vertexs[_vIndex]<<":"
<<_matrix[_vIndex][i] <<":"
<<_vertexs[i] << endl;
}
}
//让其出栈
q.pop();
//如果栈非空,
if (!q.empty())
_vIndex = q.front();
count--;
}
}
}此方法与二叉树的层序遍历有异曲同工之妙。
3.2图的深度优先遍历
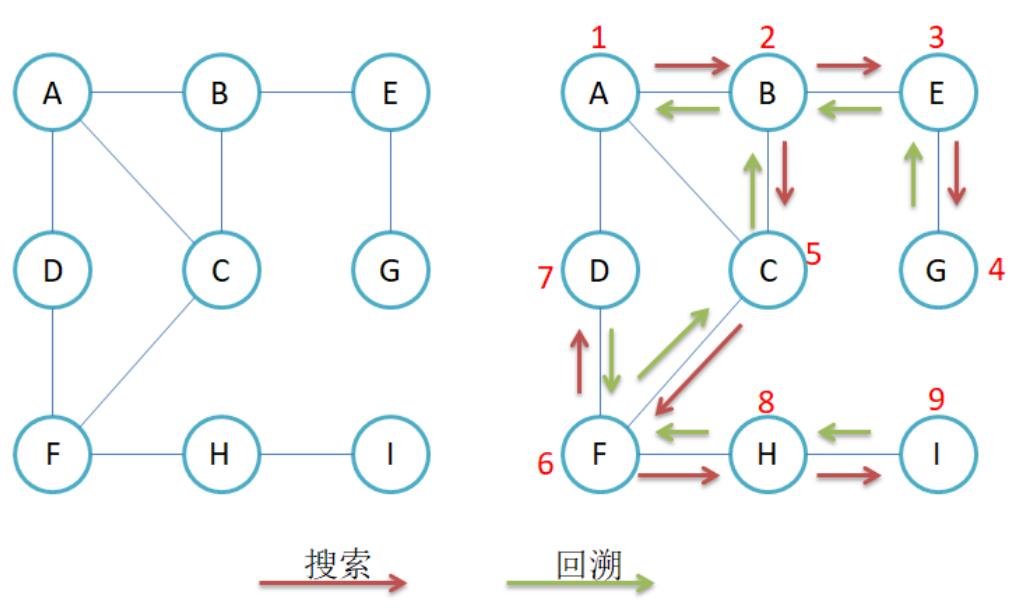
cpp
void DFS(int index, vector<bool>& v) {
for (int i = 0; i < _vertexs.size(); i++) {
if (v[i] == false && _matrix[index][i] != MAX_W) {
cout << _vertexs[i] << "->";
v[i] = true;
DFS(GetVertexIndex(_vertexs[i]), v);
}
}
v[index] = true;
cout << "///" << endl;
}
void _DFS(const V& scri) {//对外接口,方便传递v数组,判断是否遍历
vector<bool> v;
v.resize(_vertexs.size(), false);
int _vIndex = GetVertexIndex(scri);
v[_vIndex] = true;
cout << _vertexs[_vIndex] << "->";
for (int i = 0; i < _vertexs.size(); i++) {
if (v[i] == false && _matrix[_vIndex][i] != MAX_W) {//未遍历且有通路
cout << _vertexs[i] << "->";
DFS(i, v);
}
}
}BFS和DFS测试
cpp
void TestGraphDBFS() {
// 顶点:更多人物
string a[] = {
"张三", "李四", "王五", "赵六", "周七",
"吴八", "郑九", "王十", "刘十一", "陈十二"
};
Graph<string, int, MAX_W> g1(a, sizeof(a) / sizeof(string));
// 添加边:更复杂的关系(无向图)
g1.AddEdge("张三", "李四", 100);
g1.AddEdge("张三", "王五", 200);
g1.AddEdge("王五", "赵六", 30);
g1.AddEdge("王五", "周七", 30);
g1.AddEdge("李四", "吴八", 50);
g1.AddEdge("吴八", "郑九", 70);
g1.AddEdge("郑九", "王十", 40);
g1.AddEdge("周七", "刘十一", 60);
g1.AddEdge("刘十一", "陈十二", 80);
g1.AddEdge("陈十二", "张三", 90); // 形成一个环
// 测试 BFS(广度优先)
cout << "======================" << endl;
cout << "BFS starting from 张三:" << endl;
g1.BFS("张三");
// 测试 DFS(深度优先)
cout << "======================" << endl;
cout << "DFS starting from 张三:" << endl;
g1._DFS("张三");
cout << "======================" << endl;
}四、最小生成树**(Minimum Spanning Tree, MST)**
连通图中的每一颗生成树,都是原图的一个极大无环子图,即:从其中删去任意一条边,生成树就不再连同;反之,在其中引入任何一条新的边,就会形成一条回路。(注意:只适用于无向图)
若连通图由n个顶点组成。则其生成树必含有n个顶点n-1条边。
因此构造最小生成树的准则有三条:
1.只能使用图中的边来构造最小生成树
2.只能恰好使用n-1条边来连接图中的n个顶点
3.选用的n-1条边不能构成回路
构造最小生成树的方法:Kruskal算法和Prim算法。这两个算法都采用了贪心算法,前者为全局上的贪心,后者为局部上的贪心。
贪心算法:指的是在问题求解中,总是做出当前看起来最好的选择。也就是说贪心算法做出的不是整体最优解,而是某种意义上的局部最优解,但这种局部最优解往往是全局最优解。但是,贪心算法并不是对所有问题都能得到整体的最优解。
1.Kruskal算法
任给一个有n个顶点的连通网络N={V,E}。
首先构造一个由这n个顶点组成,不含任何边的图G={V,NULL},其中每个顶点自成一个连通分量。
其次不断的从E中取出权值最小的边(若有多条任取其一),若该边的两个顶点来自不同的连通分量,则将边加入到G中。如此重复,直到所有的顶点都在同一个连通分量上为止。
核心:每次迭代时,选出一条具有最小权值,且两端点不在同一连通分量上的边,加入生成树
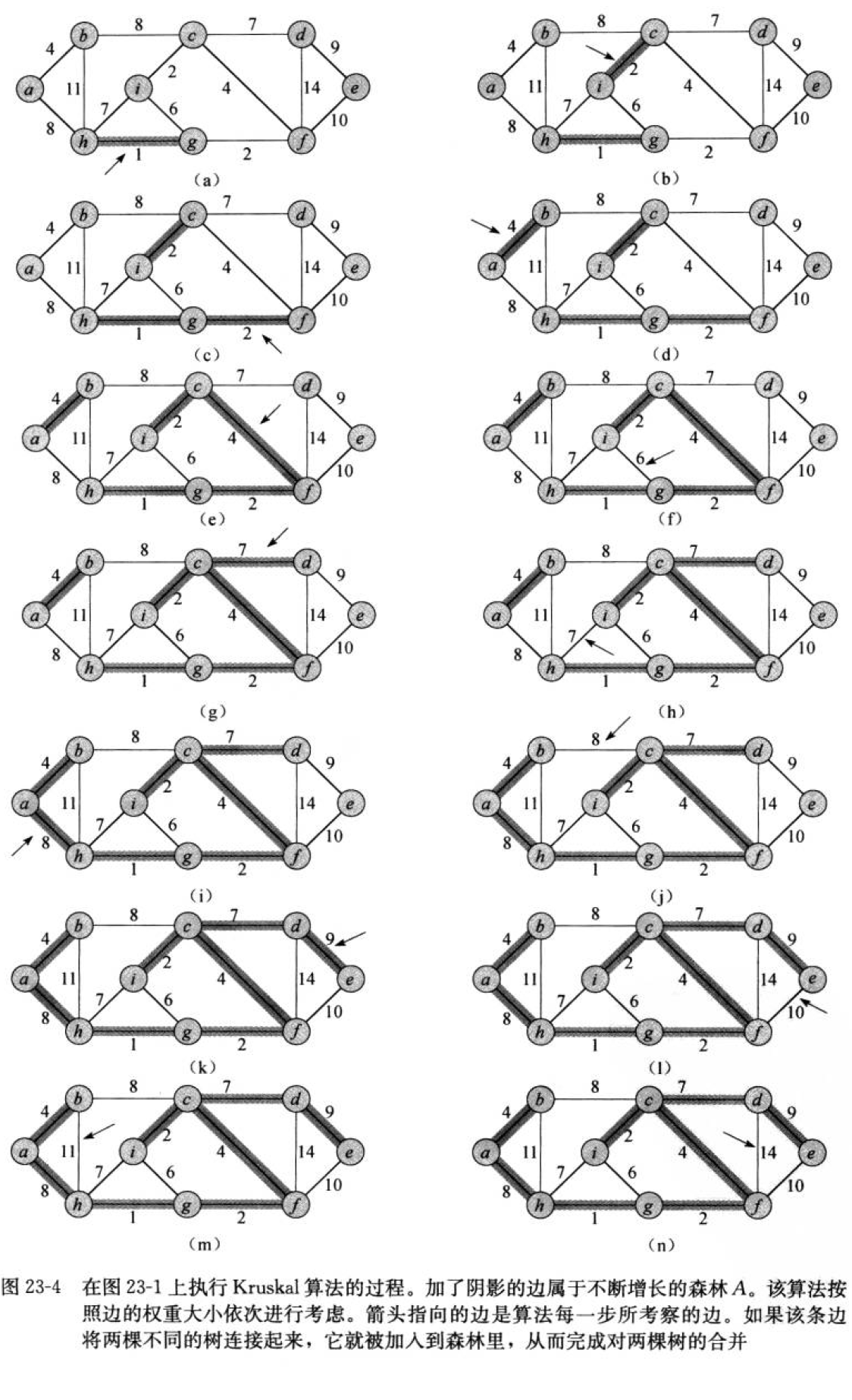
cpp
W Kruskal(self& minTree) {
minTree._vertexs = _vertexs;//构成G={V,NULL}
minTree._vIndexMap = _vIndexMap;
minTree._matrix.resize(_vertexs.size());//初始化邻接矩阵
for (int i = 0; i < _vertexs.size(); i++) {
minTree._matrix[i].resize(_vertexs.size(), MAX_W);
}
//定义优先级队列,自定义比较(按权值比较)
priority_queue<Edge, vector<Edge>, greater<Edge>> minQueue;
for (int i = 0; i < _vertexs.size(); i++) {
for (int j = 0; j < _vertexs.size(); j++) {
//将所有的边都放入minQueue中
if (_matrix[i][j] != MAX_W) {
minQueue.push(Edge(i, j, _matrix[i][j]));
}
}
}
size_t n = _vertexs.size();
//定义并查集来判环
UnionFindSet<int> ufs(n);
W total = W();//路径长度
size_t i = 0;
while (i < _vertexs.size() && !minQueue.empty()) {
Edge e = minQueue.top();//找出最小的边
if (!ufs.isUnion(e._dest, e._scri)) {//判断该边会不会构成环
minTree._AddEdge(e._dest, e._scri, e._w);
total += e._w;
ufs.merge(e._dest, e._scri);//将两顶点放入并查集
cout << (char)(e._scri + 'a') << "->" <<(char)( e._dest+'a') << endl;
i++;
}
minQueue.pop();
}
if (i == n - 1) {//找到n-1条边了
return total;
}
else {//可能并不是连通图
return W();
}
}2.Prim算法
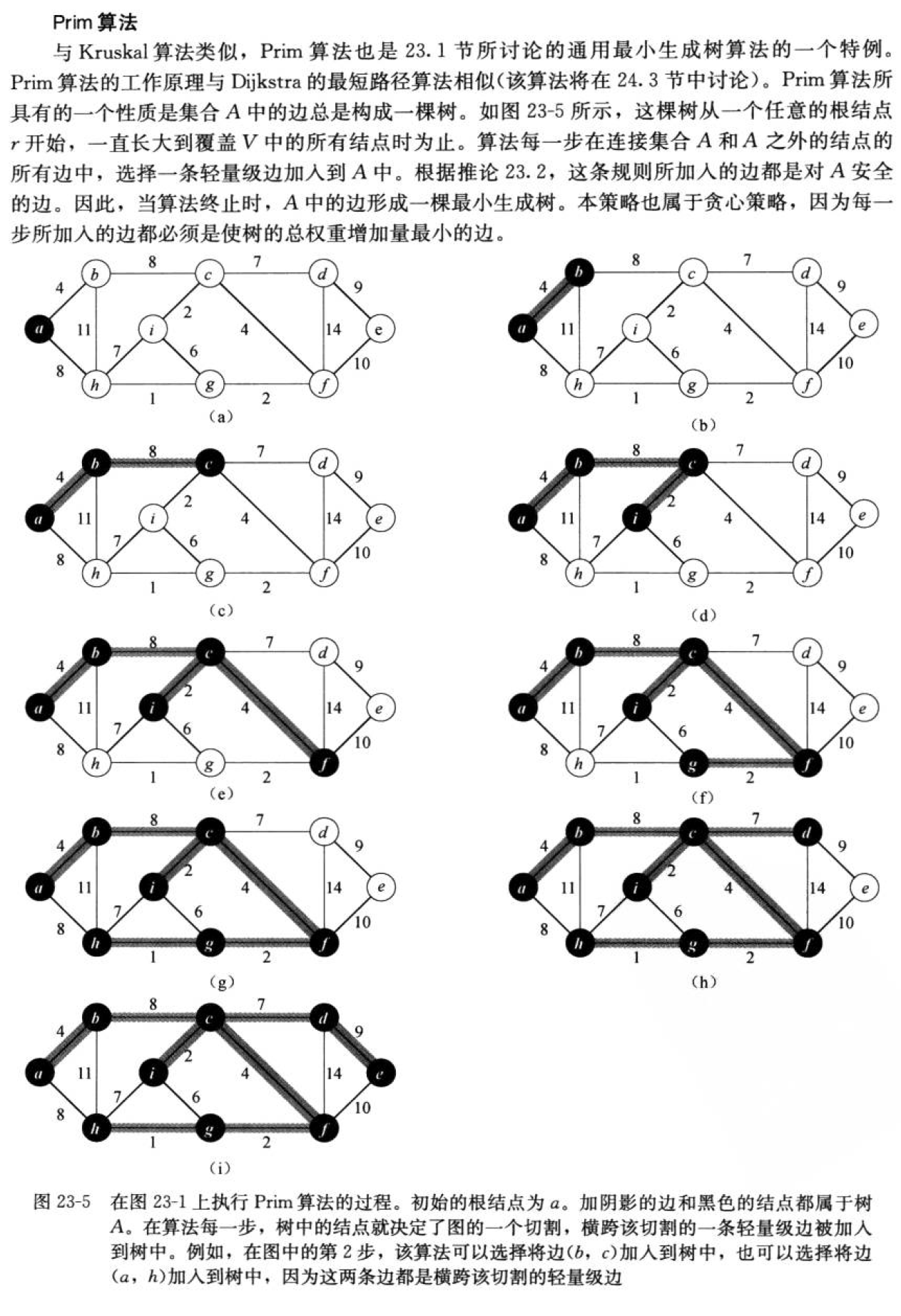
cpp
W Prim(self& minTree, const V& scri) {
//初始化
minTree._vertexs = _vertexs;
minTree._vIndexMap = _vIndexMap;
minTree._matrix.resize(_vertexs.size());
for (int i = 0; i < _vertexs.size(); i++) {
minTree._matrix[i].resize(_vertexs.size(), MAX_W);
}
//定义优先级队列
priority_queue<Edge, vector<Edge>, greater<Edge>> minQueue;
size_t n = _vertexs.size();//为顶点个数
int index = _vIndexMap[scri];//起点的下标
//sc数组存储是否可以当做起点
vector<bool> sc;
sc.resize(n, false);
sc[index] = true;
//des数组存储是否可以当终点
vector<bool> des;
des.resize(n,true);
des[index] = false;
W total = W();
size_t i = 0;
do{
//先将起点所邻接的边插入优先级队列
for (int i = 0; i < n; i++) {
//两顶点需满足起点能做起点,终点能做终点
if (_matrix[index][i] != MAX_W&&sc[index]==true&&des[i]==true) {
minQueue.push(Edge(index, i, _matrix[index][i]));
}
}
Edge e = minQueue.top();
//起点和终点都能做,才能添加
if (sc[e._scri] == true&&des[e._dest]==true) {
minTree._AddEdge(e._scri, e._dest, e._w);
total += e._w;
//做了终点的才能作为起点
sc[e._dest] = true;
//做了起点的就不能做终点
//否则会成环
des[e._dest] = false;
i++;
cout << (char)(e._scri + 'a') << "->" << (char)(e._dest + 'a') << endl;
index = e._dest;
}
minQueue.pop();
}while ( i<n&&!minQueue.empty());
if (i == n - 1) {
return total;
}
else {
return W();
}
}测试代码如下
cpp
void test05() {
const char* str = "abcdefghi";
Graph<char, int,MAX_W,false> g(str, strlen(str));
g.AddEdge('a', 'b', 4);
g.AddEdge('a', 'h', 8);
g.AddEdge('a', 'h', 9);
g.AddEdge('b', 'c', 8);
g.AddEdge('b', 'h', 11);
g.AddEdge('c', 'i', 2);
g.AddEdge('c', 'f', 4);
g.AddEdge('c', 'd', 7);
g.AddEdge('d', 'f', 14);
g.AddEdge('d', 'e', 9);
g.AddEdge('e', 'f', 10);
g.AddEdge('f', 'g', 2);
g.AddEdge('g', 'h', 1);
g.AddEdge('g', 'i', 6);
g.AddEdge('h', 'i', 7);
g.Print();
Graph<char, int,MAX_W,false> kminTree;
cout << "Kruskal:" << g.Kruskal(kminTree) << endl;
kminTree.Print();
Graph<char, int,MAX_W,false> pminTree;
cout << "Prim:" << g.Prim(pminTree, 'c') << endl;
pminTree.Print();
}五、最短路径
最短路径问题:从带权有向图G中某点出发,找出通往另一个顶点的最短路径,最短也就是沿路径各边的权值总和达到最小。
1.单源最短路径------Dijkstra算法
单源最短路径问题:给定一个图G=(V,E)求源节点s∈V到图中每一个结点v∈V的最短路径。 Dijkstra算法就适用于解决带权重的有向图上的单源最短路径问题,同时要求图中所有边的权重非负。一般在求解最短路径的时候都是已知一个起点和一个终点,所以用Dijkstra算法求解过后也就得到了所需起点到终点的最短路径。
针对一个带权有向图G,将所有结点分为两组S和Q,S是已经确定最短路径的集合,在初始时为空(将源节点放入其中,毕竟自己到自己的距离为0),Q为其余未确定的最短路径的结点的集合,每次从Q中找出一个起点到该点的代价最小的结点u,将u从Q中移出去并放入S中,对u的每一个相邻结点都做松弛操作。
松弛操作 :即对每一个相邻结点v,判断源结点s到结点u的代价与u到v的代价和是否比原来的s到v的代价更小,若更小,则更新原来的代价为s-u-v的代价的和,否则维持原样。
如此循环一直到集合Q为空,即所有结点都已经查找过一边,并确定最短路径。至于一些起点到达不了的结点在算法循环后,其代价仍为初始设定的值,不发生变化。
Dijkstra算法存在的问题是不支持图中带负权的路径,如果带有负权路径,则可能会失效。
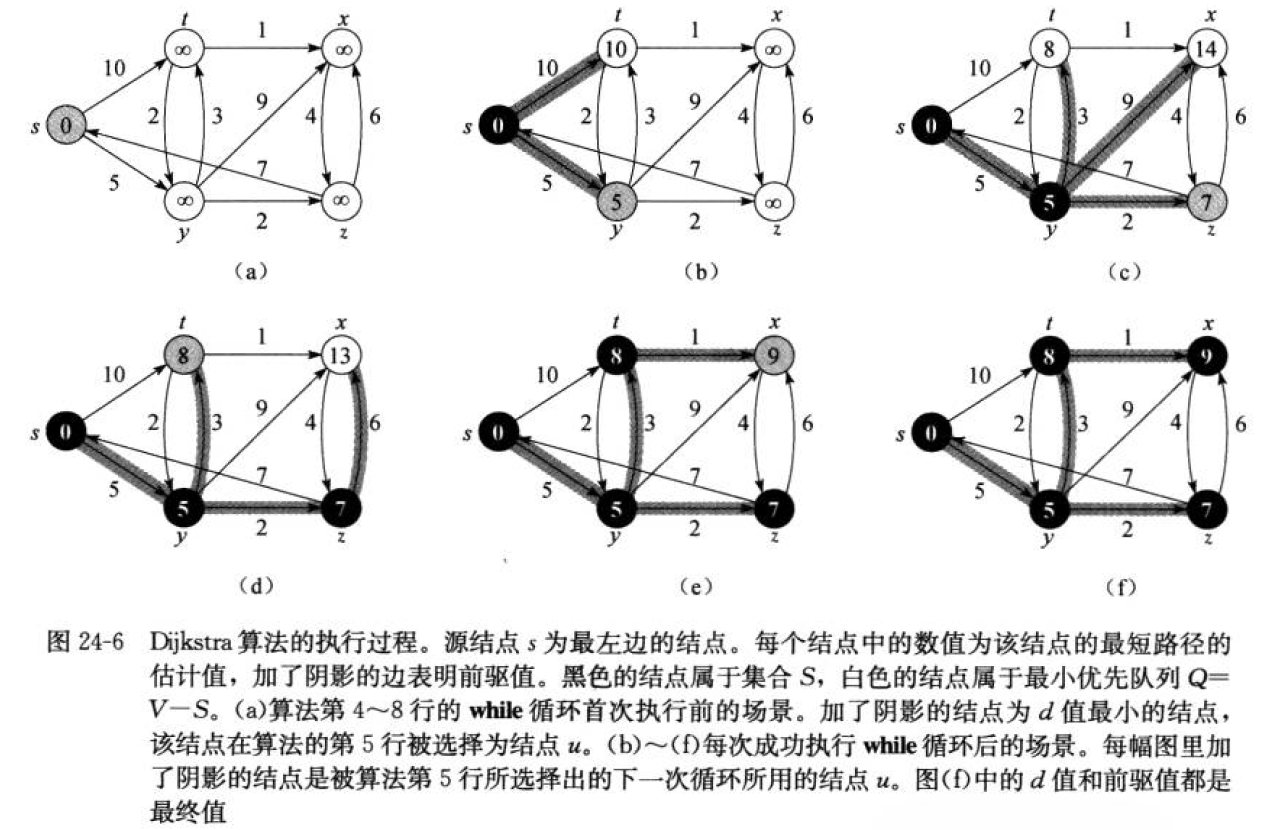
cpp
void Dijkstra(const V& scr, vector<int>& dis, vector<int>& pPath) {
//找到scr结点所对应的下标
int scri = _vIndexMap[scr];
//n为元素的总数
int n = _vertexs.size();
//dis为源结点到各个结点的最短距离
dis.resize(n, MAX_W);
//pPath为各个结点的前一个结点的下标
pPath.resize(n, -1);
//表示该结点是否已经找到最短距离
vector<bool> S;
S.resize(n, false);
S[scri] = true;
dis[scri] = W();
pPath[scri] = scri;
//找n个顶点的最短路径
for (int i = 0; i < n; i++) {
//每次初始化
W min = MAX_W;
size_t u =scri;
//找所有未探明的s能连通的最短路径
for (int j = 0; j< n; j++) {
if (S[j] == false &&dis[j]< min) {
min = dis[j];//不能用_metrix[scri][j]因为这是由scri指向j的和scri到j的距离不一样
u = j;
}
}
//找不见就给起点更新一下(没什么影响)
S[u] = true;
//更新该结点连接出去的结点的最短路径的值
for (int k = 0; k < n; k++) {
if (S[k] == false && _matrix[u][k]!=MAX_W&&dis[u] + _matrix[u][k] < dis[k]) {
dis[k] = dis[u] + _matrix[u][k];
pPath[k] = u;
}
}
}
}如何确定这个最短路径呢?根据贪心算法,每一次找当前结点引发最短的那条路
(不会发生多个路径反而距离更小,因为没有负路径,走其他路径第一步就变长了)
当前结点引发的最短的那条不会后来发生改变吗?
(不会,因为我们最开始由源节点开始遍历的,在遍历的过程中最短路径肯定是由遍历到当前结点及之前确定的,因为再继续遍历下去,会走的路程一定比当前结点指向的最短路径长)
到一个结点的最短距离要么是直接相连,要么是在遍历过程中第一次发现最短距离,因为再之后的路径一定比遍历过程中第一次发现最短路径要长。
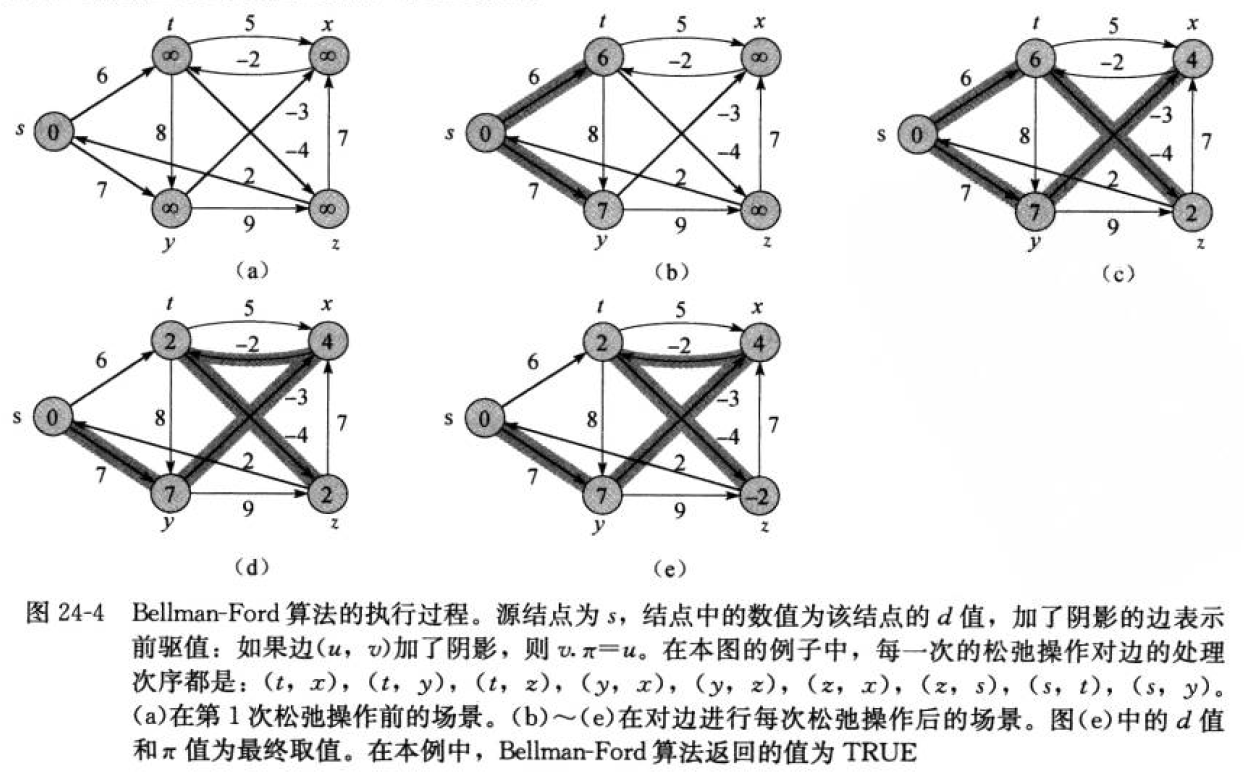
2.单源最短路径--Bellman-Ford算法
Dijkstra算法只能解决正权图的单源最短路径问题,但有些题目会出现负权图。这时这个算法就不能帮助我们解决问题了,而Bellman-Ford算法可以解决负权图的单源最短路径问题。它的优点就是可以解决有负权边的最短路径问题,而且可以用来判断是否有负权回路。它也有明显的缺点,他的时间复杂度为O(N*E)(N为点数E为边数)像这里我们用邻接矩阵实现,那么遍历所有的边的数量的时间复杂度就为O(N^3),是一种暴力求解更新。
cpp
bool BellmanFord(const V& src, vector<W>& dis, vector<int>& pPath)
{//初始化
size_t srci = _vIndexMap[src];
size_t n = _vertexs.size();
dis.resize(n, MAX_W);
pPath.resize(n, -1);
pPath[srci] = srci;
dis[srci] = W();
for(int k=0;k<n-1;k++){
bool isright = true;//判断是否已经完成求解
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
//松弛算法
if (_matrix[i][j] != MAX_W && dis[i] + _matrix[i][j] < dis[j]) {
dis[j] = dis[i] + _matrix[i][j];
pPath[j] = i;
isright = false;
}
}
}
if (isright) {
break;
}
}
//检查是否有负权回路
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (_matrix[i][j] != MAX_W && dis[i] + _matrix[i][j] < dis[j]) {
return false;
}
}
}
return true;
}Bellman-Ford算法通过逐步松弛操作,每次遍历都能确定部分顶点的最短路径,最终在V-1次遍历后确定所有的顶点的最短路径(或者检测到负权环)
第一次遍历,会将源节点引发的经过边数为一的结点全部找出,其中必然存在一条边数为一的最短路径。(可不可能走多条边,然后最短?不,因为走多条边也会产生出新的一条边)
第二次遍历,会将源节点引发的经过边数为二的结点全部找出,其中必然存在一条边数为二的最短路径......
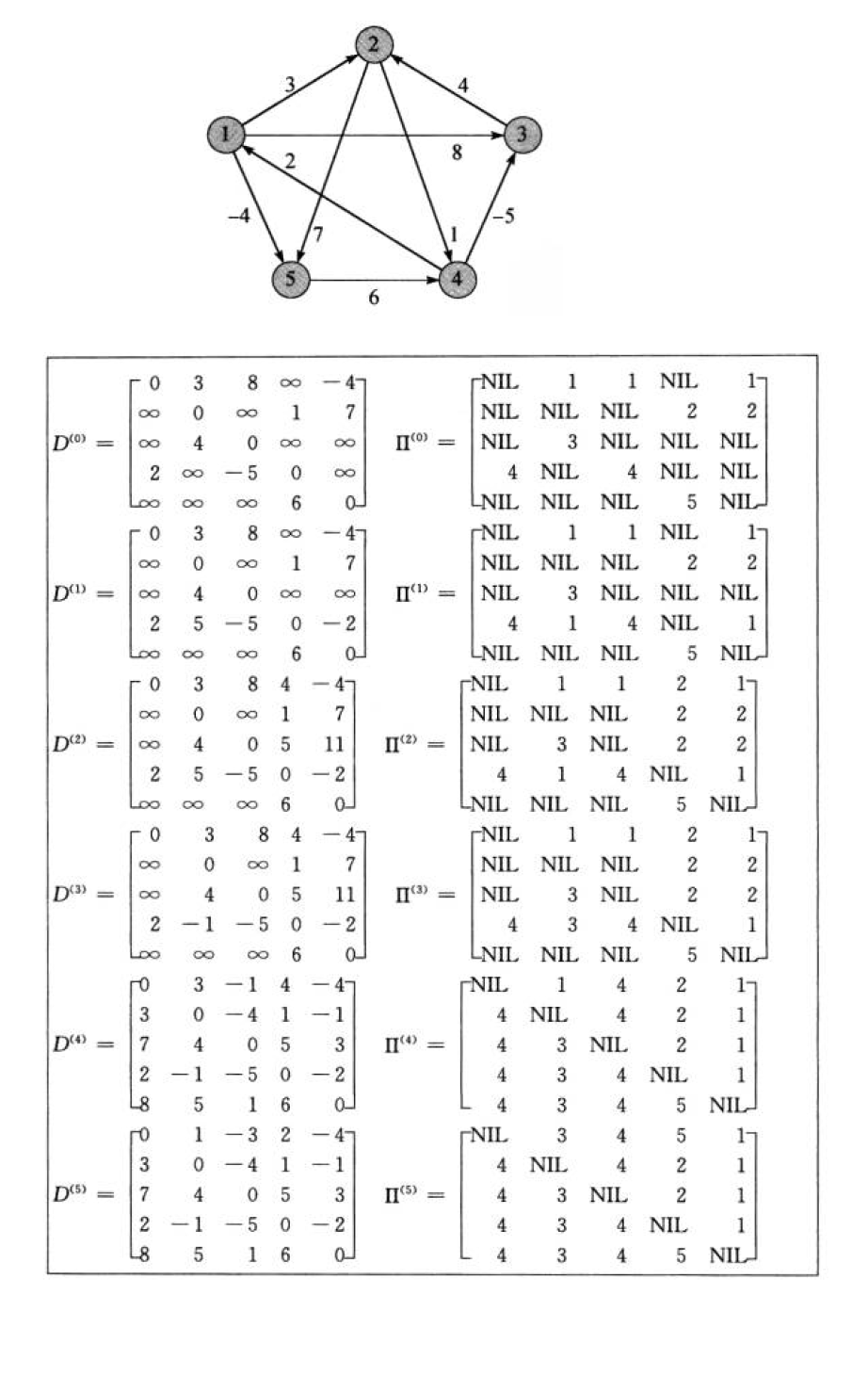
3.多源最短路径--Floyed-Warshall算法
Floyed-Warshall算法是解决任意两点间的最短路径的一种算法。
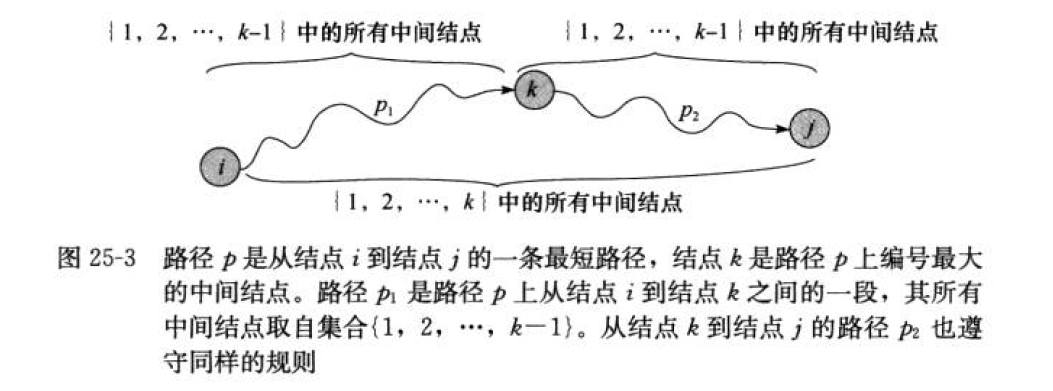
Floyd算法考虑的是一条最短路径的中间节点,即简单路径p={v1......vn}上除了v1和vn的任意结点。
设k为p的一个中间结点。那么从i到j的最短路径就划分为i->k->j两段最短路径p1和p2。p1是从i到k且中间结点属于{1,2,......k-1}取得的一条最短路径,p2是从k到j且中间结点属于{1,2,......k-1}取得的一条最短路径。

cpp
void FloydWarShall(vector<vector<W>>& vvDist, vector<vector<int>>&vvpPath)
{
//初始化
size_t n = _vertexs.size();
//这里会建立两个矩阵
//vvDist为最短距离矩阵,为i到j的最短距离
//pPath为路径矩阵,为i到j路径下指向j的结点下标
vvDist.resize(n);
vvpPath.resize(n);
for (int i = 0; i < n; i++) {
vvDist[i].resize(n, MAX_W);
vvpPath[i].resize(n, -1);
}
//将图的矩阵赋给最短距离矩阵
//路径矩阵存储一开始指向其的结点下表
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (_matrix[i][j] != MAX_W) {
vvDist[i][j] = _matrix[i][j];
vvpPath[i][j] = i;
}
else//没有通路路径矩阵就存储-1
{
vvpPath[i][j] = -1;
}
if (i == j) {
vvDist[i][j] = W();
}
}
}
for (int k = 0; k < n; k++) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (vvDist[i][k]!=MAX_W&&
vvDist[k][j]!=MAX_W&&
vvDist[i][k] + vvDist[k][j] < vvDist[i][j])
{//遍历所有中间结点,如果满足i->k->j的权值小于i->j的权值,就更新
vvDist[i][j] = vvDist[i][k] + vvDist[k][j];
//注意,这里不能赋值为k,因为指向j的结点不一定是k
vvpPath[i][j] = vvpPath[k][j];
}
}
}
}
}更新过程中为什么更新过去不会影响之前的更新结果?

本课件原理讲解及图文大量参考了《算法导论》和《殷人昆 数据结构:用面向对象方法与C++语言描述 (第二版)》的内容,代码均为自己实现。