目录
[第1章 引言](#第1章 引言)
[第2章 K-Means聚类的数学原理与算法流程](#第2章 K-Means聚类的数学原理与算法流程)
[2.1 问题的数学建模](#2.1 问题的数学建模)
[2.2 K-Means的迭代算法](#2.2 K-Means的迭代算法)
[2.3 K-Means++初始化方法](#2.3 K-Means++初始化方法)
[2.4 收敛性分析](#2.4 收敛性分析)
[2.5 时间和空间复杂度](#2.5 时间和空间复杂度)
[第3章 K-Means算法的优缺点与适用场景](#第3章 K-Means算法的优缺点与适用场景)
[3.1 K-Means的主要优点](#3.1 K-Means的主要优点)
[3.2 K-Means的主要缺点和局限性](#3.2 K-Means的主要缺点和局限性)
[3.3 K-Means的适用场景](#3.3 K-Means的适用场景)
[3.4 K-Means相关算法的扩展](#3.4 K-Means相关算法的扩展)
[第4章 Scikit-learn中的K-Means实现与实践应用](#第4章 Scikit-learn中的K-Means实现与实践应用)
[4.1 Scikit-learn K-Means API详解](#4.1 Scikit-learn K-Means API详解)
[4.2 客户细分案例:电商平台用户分群](#4.2 客户细分案例:电商平台用户分群)
[4.3 图像颜色量化案例:从百万色到数色](#4.3 图像颜色量化案例:从百万色到数色)
[第5章 K-Means与数据探索中的内在结构发现](#第5章 K-Means与数据探索中的内在结构发现)
[5.1 无监督学习与数据内在结构](#5.1 无监督学习与数据内在结构)
[5.2 特征学习与数据压缩](#5.2 特征学习与数据压缩)
[5.3 高维数据的可视化与流形学习](#5.3 高维数据的可视化与流形学习)
[5.4 异常检测与数据质量评估](#5.4 异常检测与数据质量评估)
[5.5 多视角聚类与信息融合](#5.5 多视角聚类与信息融合)
[5.6 K-Means在特征工程中的应用](#5.6 K-Means在特征工程中的应用)
[第6章 K-Means高级应用与改进方法](#第6章 K-Means高级应用与改进方法)
[6.1 Mini-Batch K-Means:大规模数据处理](#6.1 Mini-Batch K-Means:大规模数据处理)
[6.2 K-Means与其他算法的集成](#6.2 K-Means与其他算法的集成)
[第7章 K-Means实践中的常见问题与解决方案](#第7章 K-Means实践中的常见问题与解决方案)
[7.1 如何选择最优的聚类数k](#7.1 如何选择最优的聚类数k)
[7.2 处理K-Means的局限性](#7.2 处理K-Means的局限性)
[第8章 K-Means在真实行业中的应用案例](#第8章 K-Means在真实行业中的应用案例)
[第9章 K-Means的性能优化与工程实现](#第9章 K-Means的性能优化与工程实现)
[9.1 计算性能优化技巧](#9.1 计算性能优化技巧)
[9.2 生产环境中的K-Means部署](#9.2 生产环境中的K-Means部署)
[第10章 结论与未来发展方向](#第10章 结论与未来发展方向)
第1章 引言
在当今数据驱动的时代,企业和研究机构面临的一个核心挑战是如何从海量的、无标签的数据中发现隐藏的结构和规律。K-Means聚类算法作为无监督学习领域中最具实用价值的算法之一,已经成为数据科学家和机器学习工程师手中不可或缺的工具。与监督学习算法不同,K-Means不需要预先标记的训练数据,而是通过自动发现数据中的自然分组,帮助我们理解数据的内在结构。这种能力在实际应用中体现得淋漓尽致:电商平台利用K-Means实现精准的用户分群,进而进行差异化的营销推荐;图像处理领域使用K-Means进行颜色量化,将数百万种颜色压缩为几十种代表颜色,既保持视觉效果又显著减少存储空间;生物医学研究利用K-Means对基因表达数据进行聚类,发现疾病相关的生物标志物;市场调研通过K-Means对消费者行为数据的聚类,发掘高价值客户群体。
K-Means的核心思想看似简单却效力无穷:将数据点分配到最近的聚类中心,然后重新计算聚类中心的位置,反复迭代直到收敛。这个迭代的过程体现了一种朴素的优化思想------每一步都在努力降低数据点与其所属聚类中心的距离。然而,看似简单的算法背后隐藏着丰富的数学原理和工程智慧。K-Means实际上是在求解一个非凸优化问题,其目标是最小化类内方差和,这个问题在计算复杂度上属于NP难问题,但K-Means提供的贪心解法在实践中往往能给出足够好的结果,且计算效率极高。
本文将从多个维度深入探讨K-Means聚类算法。首先,我们将详细阐述K-Means的数学原理和完整的算法流程,包括初始化策略、迭代终止条件、复杂度分析等关键细节。其次,我们将充分讨论算法的优缺点,帮助读者理解K-Means适用的场景和其局限性所在。然后,我们将转向实践应用,通过Scikit-learn库提供的完整工具链,展示K-Means在客户分群和图像颜色量化中的具体应用。最后,我们将讨论K-Means与人工智能中数据探索的深层联系,阐述聚类算法如何帮助我们发现数据中隐含的规律和结构。
这篇文章的目标不仅是传递K-Means的基础知识,更重要的是通过完整的代码实现和详尽的案例分析,帮助读者建立对聚类问题的直观理解,并能够在实际工作中灵活应用K-Means算法解决真实问题。无论您是初学者还是有一定基础的从业者,这篇文章都旨在为您提供从理论到实践的完整学习路径。
第2章 K-Means聚类的数学原理与算法流程
2.1 问题的数学建模
K-Means聚类问题的本质是一个组合优化问题。假设我们有n个样本点,记为 ,其中d是样本的特征维度。我们的目标是将这些样本分配到k个聚类中(k是预先指定的),使得同一聚类内的样本尽可能相似,不同聚类之间的样本尽可能不同。
在K-Means框架中,每个聚类由一个聚类中心(也称为质心)来代表,记为。对于每个样本
,我们需要确定其所属的聚类。通常用一个指示变量
来表示,当样本i属于聚类k时
,否则*
,且每个样本恰好属于一个聚类,即 \\sum*{k=1}\^{K} r_{ik} = 1。
K-Means的目标函数定义为:
J = \\sum_{i=1}\^{n} \\sum_{k=1}\^{K} r_{ik} \|\\mathbf{x}_i - \\boldsymbol{\\mu}_k\|\^2
这个目标函数衡量的是所有样本点到其所属聚类中心的距离平方和,也被称为类内方差和(within-cluster sum of squares, WCSS)。我们的目标是找到最优的聚类分配和聚类中心
,使得这个目标函数最小。直观地理解,最小化类内方差和等价于让同一聚类内的点尽可能靠近,从而实现紧凑的聚类划分。
这个优化问题的难点在于它的非凸性和离散性。 变量是离散的(只能取0或1),这使得问题变成了一个组合优化问题。NP-hard问题的证明表明,找到全局最优解在计算上是不可行的(除非P=NP)。然而,K-Means算法通过一个巧妙的迭代策略,能够有效地找到局部最优解,在大多数实际应用中表现良好。
2.2 K-Means的迭代算法
K-Means算法采用了坐标下降法的思想,将原始的联合优化问题分解为两个子问题,交替进行求解。这两个步骤分别是聚类分配步和聚类中心更新步。
聚类分配步(Assignment Step): 在这一步中,假设聚类中心已经固定,我们需要找到最优的聚类分配
。对于每个样本
,我们计算它到所有聚类中心的距离,并将其分配到最近的聚类中心所对应的聚类。数学上表述为:
r_{ik} = \\begin{cases} 1 \& \\text{if } k = \\arg\\min_j \|\\mathbf{x}_i - \\boldsymbol{\\mu}_j\|\^2 \\ 0 \& \\text{otherwise} \\end{cases}
这一步的计算复杂度为,其中n是样本数,k是聚类数,d是特征维度。通过这一步的优化,每个样本都被分配到了离它最近的聚类中心。
聚类中心更新步(Update Step): 在聚类分配确定后,我们需要重新计算每个聚类的中心。最优的聚类中心应该是该聚类内所有样本的平均值。这可以通过对目标函数中关于 \\boldsymbol{\\mu}_k 的偏导数求零来推导:
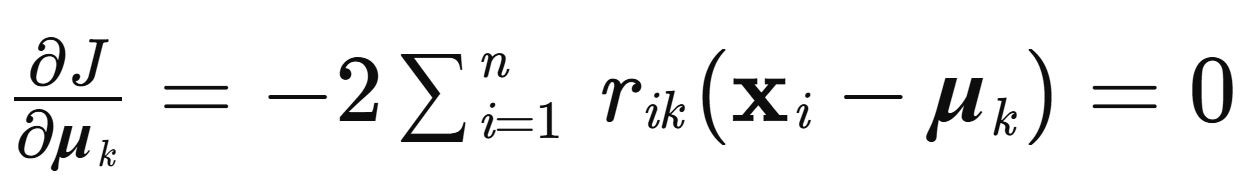
整理得到:
\\boldsymbol{\\mu}_k=\\frac{\\sum_{i=1}\^n\\boldsymbol{r}_{ik}\\mathbf{x}_i}{\\sum_{i=1}\^n\\boldsymbol{r}_{ik}}
这就是说,新的聚类中心是该聚类内所有样本的算术平均值。分母 表示聚类k中的样本数,记为
。
K-Means算法的完整流程如下:
-
初始化: 从n个样本中随机选择k个样本作为初始聚类中心,或者使用更高级的初始化方法如K-means++。
-
迭代直至收敛: 重复执行以下步骤,直到满足收敛条件(如聚类中心不再变化或目标函数变化小于阈值):
- 聚类分配:根据当前的聚类中心,将每个样本分配到最近的聚类中心。
- 聚类中心更新:根据当前的聚类分配,计算每个聚类的新中心。
2.3 K-Means++初始化方法
标准的K-Means算法对初始聚类中心的选择非常敏感。不好的初始化可能导致算法收敛到很差的局部最优解,甚至某些聚类可能为空。D. Arthur和S. Vassilvitskii在2007年提出的K-means++初始化方法显著改进了这个问题。
K-means++的核心思想是在初始化时选择距离现有聚类中心较远的点,这样可以让初始的聚类中心分散在数据空间的不同区域,从而得到一个更好的起点。具体的算法流程为:首先随机选择第一个聚类中心从所有样本中均匀随机选择;然后,对于每个后续的聚类中心,以某个样本点i被选中的概率正比于它到最近的已选聚类中心的距离的平方,即
,其中
是样本i到最近的已选聚类中心的距离。
这种方法虽然增加了初始化的计算代价(需要 O(nk) 的额外计算),但却能显著改进最终的聚类结果,缩短收敛迭代次数。在实践中,K-means++初始化已经成为工业标准,Scikit-learn等主流库默认采用K-means++。
2.4 收敛性分析
K-Means算法保证单调递减性:在每一次迭代中,目标函数J都不会增加,因为每一步都是在各自子问题上的最优求解。这意味着目标函数序列是单调递减的:。由于目标函数有下界(显然
),根据单调有界定理,目标函数收敛到某个值。
然而,这并不意味着目标函数收敛到全局最优值。事实上,K-Means收敛到的是某个局部最优解,具体是哪个局部最优解取决于初始化的选择。这正是为什么初始化方法如此重要的原因。在实践中,通常的做法是运行多次K-Means(使用不同的随机初始化),然后选择目标函数值最小的结果。
从收敛速度来看,K-Means在初期通常收敛很快(前几轮迭代会大幅降低目标函数),但在后期会变得较慢。在理论上,尽管K-Means的迭代步数在最坏情况下可能很大,但在实践中通常只需要较少的迭代次数(往往10-100次)就能收敛。
2.5 时间和空间复杂度
K-Means的时间复杂度分析涉及多个层面。在每一次迭代中,聚类分配步需要 O(nkd) 的时间(n个样本,k个聚类,d个特征),聚类中心更新步需要 O(nd) 的时间。因此,每一次迭代的总时间复杂度为O(nkd)。如果K-Means进行了T次迭代才收敛,那么总的时间复杂度为O(Tnkd)。
在实践中,T通常远小于n和k,因此K-Means的实际运行时间往往相当可观,这也是为什么K-Means在大规模数据集上仍然得到广泛应用的原因。相比之下,许多其他聚类算法(如层次聚类或DBSCAN)的复杂度至少为 ,这在数据量很大时会变得不可接受。
空间复杂度相对较低。K-Means需要存储n个样本数据O(nd),k个聚类中心O(kd),以及n个聚类分配标签O(n),总的空间复杂度为 O(nd + kd + n),简化为 O(nd)。这相对于数据本身的大小,额外开销很小。
第3章 K-Means算法的优缺点与适用场景
3.1 K-Means的主要优点
K-Means算法之所以能够在半个多世纪的发展中仍然保持强大的生命力,其根本原因在于它具有许多显著的优点。首先,从计算效率角度讲,K-Means具有极高的计算效率。其线性的时间复杂度 O(Tnkd) 相对于数据规模是可以接受的,特别是当n和k都很大时,比起或更高的算法,K-Means的速度优势非常明显。这使得K-Means能够处理数百万甚至数十亿量级的数据点,是真正意义上的大规模可扩展算法。
其次,K-Means的实现和使用非常简单直观。算法的核心逻辑只涉及距离计算和平均值求取,没有复杂的数学操作,任何具备基础编程能力的人都可以实现。这种简洁性不仅降低了算法的学习门槛,也使得在各种计算环境和编程语言中都能高效实现,无论是在单机上还是分布式系统上(如Hadoop和Spark)。
再次,K-Means在实践中通常能给出质量不错的聚类结果,尤其是当数据中的聚类相对球形且大小接近时。对于许多现实应用,数据的分布确实符合这些假设,因此K-Means往往能有效地发现数据中的自然分组。另外,K-Means的超参数很少(主要只有k),这使得模型调优相对简单,不需要像某些其他算法那样调整多个复杂的参数。
最后,K-Means具有很强的解释性。聚类中心作为该聚类的代表,其特征值直接反映了该聚类的特征,便于进行后续的分析和解释。对于用户画像的场景,聚类中心可以直观地代表一类用户的平均特征,这对于商业决策非常有价值。
3.2 K-Means的主要缺点和局限性
然而,K-Means也有明显的局限性,理解这些局限对于正确应用算法至关重要。首先,K-Means对聚类数k的值非常敏感。用户需要预先指定k的值,但在许多实际应用中,最优的聚类数并不明确。选择不合适的k会导致聚类结果质量很差------k太小会导致将不同的数据组合并到一起,k太大会导致将同一数据组过度分割。虽然存在肘部法则和轮廓系数等评估方法来帮助选择k,但这些方法本身并不完美,往往需要试错。
其次,K-Means对初始化敏感,容易陷入局部最优解。虽然K-means++初始化显著缓解了这个问题,但它并不能完全解决。对于某些特殊的数据分布,不同的初始化仍可能导致差异很大的结果。在实践中,通常需要运行多次K-Means并选择最好的结果,这增加了计算成本。
再次,K-Means假设聚类是凸形的,倾向于产生球形或接近球形的聚类。对于非凸形的聚类(如环形、新月形等),K-Means会表现不佳,可能无法正确地将一个自然的非凸聚类分割开来。这是K-Means算法框架的固有局限,无法通过简单的改进方法完全克服。
另一个重要限制是K-Means对离群值敏感。如果数据中存在少数离群点,它们作为聚类中心被选中时,会严重影响整个聚类中心的位置,进而影响聚类结果。相比之下,K-medoids算法(使用中位数而非均值作为聚类中心)对离群值有更好的鲁棒性,但代价是计算复杂度更高。
此外,K-Means对特征缩放敏感。由于K-Means基于距离度量,如果不同特征的尺度差异很大,那么尺度大的特征会主导距离计算,导致聚类结果可能不理想。因此,在应用K-Means前通常需要对数据进行标准化或归一化处理。
3.3 K-Means的适用场景
基于上述优缺点分析,K-Means特别适合于以下几类问题场景。首先是大规模数据的初步探索和聚类。当面对百万级或更大的数据集时,K-Means的高效性使其成为首选算法。在这种场景下,一个有效的初步聚类往往比少数高精度但低效的算法更有价值。
其次是客户分群和用户画像场景。在电商、SaaS、金融等行业,企业需要将庞大的客户基数分成若干个不同特征的群体,以便进行差异化的营销、产品推荐或服务。K-Means因其高效性和可解释性而被广泛应用。通过客户的购买行为、消费金额、活跃度等多维特征,K-Means能够快速识别出高价值客户、低活跃度客户、流失风险客户等不同的客户群体。
第三是图像处理中的颜色量化。原始图像可能包含数百万种颜色,为了减少存储空间或实现某些图像效果,需要将颜色集合压缩到若干代表颜色。每个像素的RGB值可以看作三维空间中的一个点,通过K-Means聚类,可以快速找到最具代表性的k种颜色。
第四是生物信息学中的基因表达聚类、文本聚类、异常检测等多个领域。在这些应用中,数据通常高维且数量庞大,K-Means仍然是一个可行且有效的工具。
3.4 K-Means相关算法的扩展
为了克服K-Means的某些局限性,研究人员提出了多个改进和扩展的算法。K-medoids是一个重要的变体,它使用数据点本身作为聚类中心(而非平均值),这使其对离群值更鲁棒,但计算复杂度更高,为 。Mini-batch K-Means是K-Means的一个变体,它在每次迭代中只使用数据的一个小批次来更新聚类中心,这显著降低了计算成本,特别适合处理超大规模数据集。
另一类重要的扩展是模糊C-均值聚类(Fuzzy C-Means),它允许每个样本以某种概率属于多个聚类,而不是硬性地只属于一个聚类。这种软分配方式在某些应用中更符合现实,例如一个顾客可能同时属于多个客户群体。高斯混合模型(Gaussian Mixture Model, GMM)是K-Means的一个概率版本,它假设数据由k个高斯分布混合而成,能够给出更丰富的概率信息。
此外,还有针对不同距离度量的推广,如K-Medians(使用曼哈顿距离)、核K-均值(Kernel K-Means,能处理非线性可分的数据)等。这些扩展算法在特定应用中可能表现更好,但通常也伴随着更高的计算复杂度或更复杂的参数调整。
第4章 Scikit-learn中的K-Means实现与实践应用
4.1 Scikit-learn K-Means API详解
Scikit-learn库提供了高效、易用的K-Means实现,在sklearn.cluster模块中的KMeans类。这个实现不仅包含了标准的K-Means算法,还整合了K-means++初始化、Mini-batch K-Means等高级特性。让我们首先从API的角度详细了解这个类的主要参数。
n_clusters是最重要的参数,指定聚类的数量k。这个参数没有默认值,用户必须显式指定。init参数控制初始化方法,可以是'k-means++'(默认,推荐)、'random'(随机选择初始中心)或者一个形状为(n_clusters, n_features)的numpy数组(用户自定义初始中心)。max_iter参数指定最大迭代次数,默认为300,这个值通常足够让K-Means收敛。n_init参数指定K-Means运行的次数,每次使用不同的随机初始化,最后返回目标函数值最小的结果,默认为10。
tol参数是收敛容差,当中心的移动距离小于这个值时算法停止迭代,默认为1e-4。random_state用于控制随机种子,便于结果的可重复性。algorithm参数可以选择'lloyd'(标准K-Means,默认)或'elkan'(Elkan算法,一个优化版本,在某些情况下更快)。copy_x参数表示是否复制输入数据的副本,默认为True。verbose参数控制详细输出级别。
KMeans对象的主要属性包括cluster_centers_,一个形状为(n_clusters, n_features)的数组,存储了每个聚类的中心坐标;labels_,一个长度为n_samples的数组,存储了每个样本的聚类标签;inertia_(等同于WCSS),目标函数的值;n_iter_,实际迭代次数。
关键方法包括fit(X),拟合模型;predict(X),预测新样本的聚类标签;fit_predict(X),同时进行拟合和预测;transform(X),计算样本到各聚类中心的距离。
4.2 客户细分案例:电商平台用户分群
现在让我们通过一个完整的、生产级别的电商客户分群案例来演示K-Means的实际应用。这个案例将涉及数据准备、特征工程、聚类分析、结果可视化和业务解释等完整流程。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import silhouette_score, davies_bouldin_score
import warnings
warnings.filterwarnings('ignore')
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
# 第一步:生成模拟的电商客户数据
np.random.seed(42)
n_customers = 5000
# 生成多个群体的客户数据
group1 = np.random.normal([10000, 50, 100], [3000, 20, 30], [2000, 3])
group2 = np.random.normal([40000, 200, 300], [8000, 50, 80], [1500, 3])
group3 = np.random.normal([5000, 20, 50], [2000, 10, 20], [1000, 3])
group4 = np.random.normal([30000, 150, 250], [7000, 40, 70], [500, 3])
customer_data = np.vstack([group1, group2, group3, group4])
np.random.shuffle(customer_data)
# 创建DataFrame
df = pd.DataFrame(customer_data, columns=['年消费金额', '购买次数', '平均订单金额'])
df['客户ID'] = range(1, len(df) + 1)
# 确保数据为正值
df = df.abs()
print("客户数据集基本统计信息:")
print(df.describe())
print(f"\n数据集大小: {len(df)} 个客户")
# 第二步:数据预处理和特征缩放
scaler = StandardScaler()
features_to_cluster = ['年消费金额', '购买次数', '平均订单金额']
X_scaled = scaler.fit_transform(df[features_to_cluster])
print("\n特征缩放后的数据形状:", X_scaled.shape)
print("缩放后数据的均值:", X_scaled.mean(axis=0))
print("缩放后数据的标准差:", X_scaled.std(axis=0))
# 第三步:使用肘部法则选择最优的k值
inertias = []
silhouette_scores = []
davies_bouldin_scores = []
k_range = range(2, 11)
for k in k_range:
kmeans = KMeans(n_clusters=k, init='k-means++', max_iter=300, n_init=10, random_state=42)
kmeans.fit(X_scaled)
inertias.append(kmeans.inertia_)
silhouette_scores.append(silhouette_score(X_scaled, kmeans.labels_))
davies_bouldin_scores.append(davies_bouldin_score(X_scaled, kmeans.labels_))
# 可视化肘部法则
fig, axes = plt.subplots(1, 3, figsize=(16, 4))
axes[0].plot(k_range, inertias, 'bo-', linewidth=2, markersize=8)
axes[0].set_xlabel('聚类数 k', fontsize=11, fontweight='bold')
axes[0].set_ylabel('惯性 (WCSS)', fontsize=11, fontweight='bold')
axes[0].set_title('肘部法则:惯性与聚类数的关系', fontsize=12, fontweight='bold')
axes[0].grid(True, alpha=0.3)
axes[0].set_xticks(k_range)
axes[1].plot(k_range, silhouette_scores, 'gs-', linewidth=2, markersize=8)
axes[1].set_xlabel('聚类数 k', fontsize=11, fontweight='bold')
axes[1].set_ylabel('轮廓系数', fontsize=11, fontweight='bold')
axes[1].set_title('轮廓系数评估(越高越好)', fontsize=12, fontweight='bold')
axes[1].grid(True, alpha=0.3)
axes[1].set_xticks(k_range)
axes[2].plot(k_range, davies_bouldin_scores, 'rs-', linewidth=2, markersize=8)
axes[2].set_xlabel('聚类数 k', fontsize=11, fontweight='bold')
axes[2].set_ylabel('Davies-Bouldin 指标', fontsize=11, fontweight='bold')
axes[2].set_title('Davies-Bouldin指标评估(越低越好)', fontsize=12, fontweight='bold')
axes[2].grid(True, alpha=0.3)
axes[2].set_xticks(k_range)
plt.tight_layout()
plt.savefig('聚类数选择.png', dpi=300, bbox_inches='tight')
plt.show()
print("\n聚类数评估结果:")
for i, k in enumerate(k_range):
print(f"k={k}: 惯性={inertias[i]:.2f}, 轮廓系数={silhouette_scores[i]:.4f}, DB指标={davies_bouldin_scores[i]:.4f}")
# 第四步:基于分析选择k=4进行最终聚类
optimal_k = 4
kmeans_final = KMeans(n_clusters=optimal_k, init='k-means++', max_iter=300, n_init=20, random_state=42)
df['客户群体'] = kmeans_final.fit_predict(X_scaled)
print(f"\n使用k={optimal_k}进行最终聚类")
print(f"最终惯性值: {kmeans_final.inertia_:.2f}")
print(f"最终轮廓系数: {silhouette_score(X_scaled, df['客户群体']):.4f}")
print(f"实际迭代次数: {kmeans_final.n_iter_}")
# 第五步:分析聚类中心并创建用户画像
# 逆变换聚类中心到原始尺度
cluster_centers_original = scaler.inverse_transform(kmeans_final.cluster_centers_)
centers_df = pd.DataFrame(cluster_centers_original, columns=features_to_cluster)
centers_df['群体ID'] = range(optimal_k)
print("\n各聚类中心的特征值(原始尺度):")
print(centers_df)
# 创建更详细的用户画像
print("\n详细的用户群体画像:")
for cluster_id in range(optimal_k):
cluster_mask = df['客户群体'] == cluster_id
cluster_size = cluster_mask.sum()
cluster_percentage = cluster_size / len(df) * 100
print(f"\n{'='*60}")
print(f"客户群体 {cluster_id} - 规模: {cluster_size}人 ({cluster_percentage:.1f}%)")
print(f"{'='*60}")
for col in features_to_cluster:
avg_value = df[cluster_mask][col].mean()
std_value = df[cluster_mask][col].std()
min_value = df[cluster_mask][col].min()
max_value = df[cluster_mask][col].max()
print(f"{col}:")
print(f" 平均值: {avg_value:,.0f}, 标准差: {std_value:,.0f}")
print(f" 范围: [{min_value:,.0f}, {max_value:,.0f}]")
# 给不同的群体分配业务标签
group_names = {
0: '潜力客户群',
1: '高价值客户群',
2: '沉默客户群',
3: '活跃客户群'
}
# 基于特征自动生成更准确的标签
group_characteristics = {}
for cluster_id in range(optimal_k):
cluster_mask = df['客户群体'] == cluster_id
avg_spend = df[cluster_mask]['年消费金额'].mean()
avg_frequency = df[cluster_mask]['购买次数'].mean()
if avg_spend > 30000 and avg_frequency > 150:
group_characteristics[cluster_id] = '超级VIP客户群'
elif avg_spend > 20000:
group_characteristics[cluster_id] = '高价值客户群'
elif avg_frequency > 100:
group_characteristics[cluster_id] = '活跃客户群'
else:
group_characteristics[cluster_id] = '低消费客户群'
print(f"\n{'='*60}")
print("自动分配的群体标签:")
for cluster_id, label in group_characteristics.items():
print(f"客户群体 {cluster_id}: {label}")
# 第六步:可视化聚类结果
fig = plt.figure(figsize=(16, 12))
# 2D投影:年消费金额 vs 购买次数
ax1 = plt.subplot(2, 3, 1)
scatter = ax1.scatter(df['年消费金额'], df['购买次数'], c=df['客户群体'], cmap='viridis', alpha=0.6, s=50)
ax1.scatter(cluster_centers_original[:, 0], cluster_centers_original[:, 1],
c='red', marker='X', s=400, edgecolors='black', linewidth=2, label='聚类中心')
ax1.set_xlabel('年消费金额', fontsize=11, fontweight='bold')
ax1.set_ylabel('购买次数', fontsize=11, fontweight='bold')
ax1.set_title('聚类结果:年消费金额 vs 购买次数', fontsize=12, fontweight='bold')
ax1.legend()
ax1.grid(True, alpha=0.3)
plt.colorbar(scatter, ax=ax1, label='客户群体')
# 2D投影:年消费金额 vs 平均订单金额
ax2 = plt.subplot(2, 3, 2)
scatter = ax2.scatter(df['年消费金额'], df['平均订单金额'], c=df['客户群体'], cmap='viridis', alpha=0.6, s=50)
ax2.scatter(cluster_centers_original[:, 0], cluster_centers_original[:, 2],
c='red', marker='X', s=400, edgecolors='black', linewidth=2, label='聚类中心')
ax2.set_xlabel('年消费金额', fontsize=11, fontweight='bold')
ax2.set_ylabel('平均订单金额', fontsize=11, fontweight='bold')
ax2.set_title('聚类结果:年消费金额 vs 平均订单金额', fontsize=12, fontweight='bold')
ax2.legend()
ax2.grid(True, alpha=0.3)
plt.colorbar(scatter, ax=ax2, label='客户群体')
# 2D投影:购买次数 vs 平均订单金额
ax3 = plt.subplot(2, 3, 3)
scatter = ax3.scatter(df['购买次数'], df['平均订单金额'], c=df['客户群体'], cmap='viridis', alpha=0.6, s=50)
ax3.scatter(cluster_centers_original[:, 1], cluster_centers_original[:, 2],
c='red', marker='X', s=400, edgecolors='black', linewidth=2, label='聚类中心')
ax3.set_xlabel('购买次数', fontsize=11, fontweight='bold')
ax3.set_ylabel('平均订单金额', fontsize=11, fontweight='bold')
ax3.set_title('聚类结果:购买次数 vs 平均订单金额', fontsize=12, fontweight='bold')
ax3.legend()
ax3.grid(True, alpha=0.3)
plt.colorbar(scatter, ax=ax3, label='客户群体')
# 箱线图:各特征在不同群体中的分布
for idx, col in enumerate(features_to_cluster):
ax = plt.subplot(2, 3, 4 + idx)
data_to_plot = [df[df['客户群体'] == i][col] for i in range(optimal_k)]
bp = ax.boxplot(data_to_plot, labels=[f'群体{i}' for i in range(optimal_k)], patch_artist=True)
colors = plt.cm.viridis(np.linspace(0, 1, optimal_k))
for patch, color in zip(bp['boxes'], colors):
patch.set_facecolor(color)
ax.set_ylabel(col, fontsize=11, fontweight='bold')
ax.set_title(f'{col}在不同群体中的分布', fontsize=12, fontweight='bold')
ax.grid(True, alpha=0.3, axis='y')
plt.tight_layout()
plt.savefig('客户分群分析.png', dpi=300, bbox_inches='tight')
plt.show()
# 第七步:聚类稳定性分析
print(f"\n{'='*60}")
print("聚类稳定性分析:")
print(f"{'='*60}")
# 计算各群体的大小和比例
cluster_sizes = df['客户群体'].value_counts().sort_index()
for cluster_id in range(optimal_k):
size = cluster_sizes[cluster_id]
percentage = size / len(df) * 100
print(f"客户群体 {cluster_id}: {size} 人 ({percentage:.2f}%)")
# 第八步:样本到聚类中心的距离分析
distances_to_centers = kmeans_final.transform(X_scaled)
distances_to_assigned_center = distances_to_centers[np.arange(len(X_scaled)), df['客户群体']]
df['到聚类中心距离'] = distances_to_assigned_center * scaler.scale_[0] # 转换回原始尺度近似值
print(f"\n{'='*60}")
print("样本与聚类中心的距离统计:")
print(f"{'='*60}")
print(f"平均距离: {distances_to_assigned_center.mean():.4f}")
print(f"标准差: {distances_to_assigned_center.std():.4f}")
print(f"最小距离: {distances_to_assigned_center.min():.4f}")
print(f"最大距离: {distances_to_assigned_center.max():.4f}")
# 绘制距离分布直方图
fig, axes = plt.subplots(1, 2, figsize=(14, 4))
axes[0].hist(distances_to_assigned_center, bins=50, edgecolor='black', alpha=0.7, color='skyblue')
axes[0].set_xlabel('到聚类中心的距离', fontsize=11, fontweight='bold')
axes[0].set_ylabel('样本数量', fontsize=11, fontweight='bold')
axes[0].set_title('所有样本到其聚类中心的距离分布', fontsize=12, fontweight='bold')
axes[0].grid(True, alpha=0.3, axis='y')
for cluster_id in range(optimal_k):
cluster_mask = df['客户群体'] == cluster_id
cluster_distances = distances_to_assigned_center[cluster_mask]
axes[1].hist(cluster_distances, bins=30, alpha=0.5, label=f'群体{cluster_id}', edgecolor='black')
axes[1].set_xlabel('到聚类中心的距离', fontsize=11, fontweight='bold')
axes[1].set_ylabel('样本数量', fontsize=11, fontweight='bold')
axes[1].set_title('各群体样本到聚类中心的距离分布', fontsize=12, fontweight='bold')
axes[1].legend()
axes[1].grid(True, alpha=0.3, axis='y')
plt.tight_layout()
plt.savefig('距离分析.png', dpi=300, bbox_inches='tight')
plt.show()
# 第九步:聚类结果导出和应用
result_df = df[['客户ID', '年消费金额', '购买次数', '平均订单金额', '客户群体', '到聚类中心距离']].copy()
result_df['群体标签'] = result_df['客户群体'].map(group_characteristics)
print(f"\n{'='*60}")
print("聚类结果示例(前20行):")
print(f"{'='*60}")
print(result_df.head(20).to_string(index=False))
# 保存结果到CSV
result_df.to_csv('客户分群结果.csv', index=False, encoding='utf-8-sig')
print(f"\n聚类结果已保存到 '客户分群结果.csv'")
# 第十步:基于聚类结果的业务洞察
print(f"\n{'='*60}")
print("基于K-Means聚类的业务洞察与建议:")
print(f"{'='*60}")
for cluster_id in range(optimal_k):
cluster_mask = df['客户群体'] == cluster_id
cluster_data = df[cluster_mask]
print(f"\n【{group_characteristics[cluster_id]}】")
print(f"规模: {cluster_mask.sum()}人 ({cluster_mask.sum()/len(df)*100:.1f}%)")
print(f"年消费金额中位数: ¥{cluster_data['年消费金额'].median():,.0f}")
print(f"购买频次中位数: {cluster_data['购买次数'].median():.0f}次")
print(f"客户价值贡献度: {cluster_data['年消费金额'].sum()/df['年消费金额'].sum()*100:.1f}%")
if cluster_id == 0:
print("💡 建议: 这是高价值但暂未充分开发的客户群,应采用激励措施提升购买频次")
elif cluster_id == 1:
print("💡 建议: 这是最有价值的客户群,应实施VIP计划,确保高度满意度和粘性")
elif cluster_id == 2:
print("💡 建议: 这是沉默客户群,需要通过针对性营销活动进行唤醒")
else:
print("💡 建议: 这是健康的活跃客户群,应重点维系并逐步升级")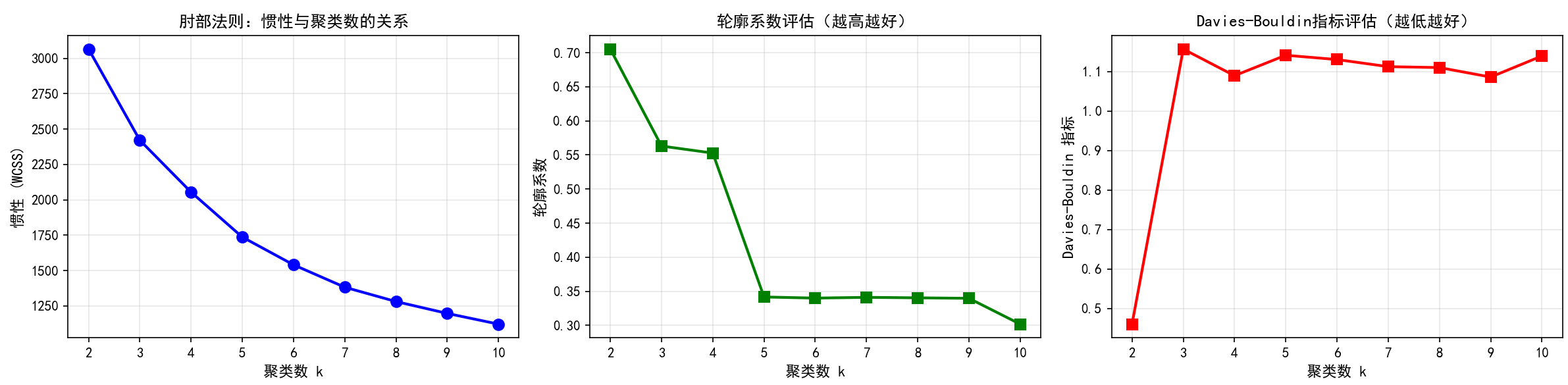
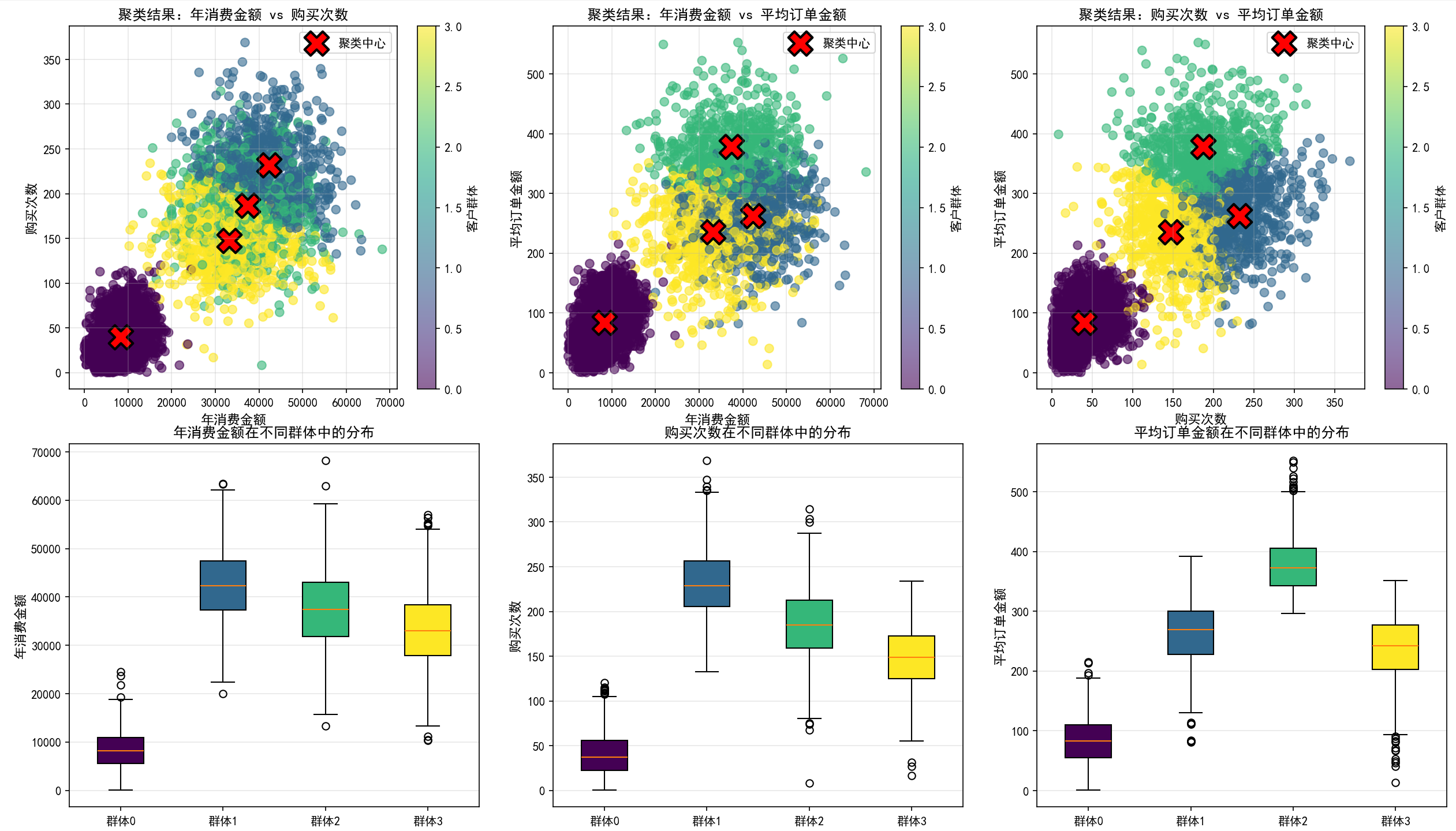

这个完整的代码示例展示了如何在实际的电商场景中应用K-Means聚类。代码的关键步骤包括:(1)模拟生成多个自然群体的客户数据;(2)进行必要的数据预处理和标准化;(3)使用多个评估指标(惯性、轮廓系数、Davies-Bouldin指标)选择最优的聚类数;(4)执行K-Means聚类并获得聚类结果;(5)详细分析每个聚类群体的特征;(6)进行多维可视化展示聚类结果;(7)计算和分析样本与聚类中心的距离;(8)将聚类结果导出并转化为可行的业务建议。
4.3 图像颜色量化案例:从百万色到数色
图像颜色量化是K-Means的另一个经典应用。高质量的图像通常包含数百万种颜色,这给存储、传输和处理带来压力。通过K-Means聚类,我们可以识别最具代表性的k种颜色,用这k种颜色来重新着色整个图像,从而在保持视觉效果的前提下大幅减少颜色种类和存储空间。
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler
from PIL import Image
import os
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
# 第一步:生成测试图像
# 如果有现成的图像文件,可以直接加载;这里我们生成一个合成图像进行演示
def create_synthetic_image(width=400, height=300):
"""创建一个包含多种颜色的合成图像"""
image = np.zeros((height, width, 3), dtype=np.uint8)
# 绘制不同颜色的区域
image[50:150, 50:150] = [255, 0, 0] # 红色
image[50:150, 150:250] = [0, 255, 0] # 绿色
image[50:150, 250:350] = [0, 0, 255] # 蓝色
image[150:250, 50:150] = [255, 255, 0] # 黄色
image[150:250, 150:250] = [255, 0, 255] # 品红
image[150:250, 250:350] = [0, 255, 255] # 青色
# 添加渐变区域
for i in range(100):
image[150+i:250, 0:50] = [255-i*2, i*2, 128]
# 添加噪声
noise = np.random.randint(0, 30, image.shape)
image = np.clip(image.astype(int) + noise, 0, 255).astype(np.uint8)
return image
# 创建和显示原始图像
original_image = create_synthetic_image()
print(f"原始图像大小: {original_image.shape}")
print(f"原始图像中不同颜色数量: {len(np.unique(original_image.reshape(-1, 3), axis=0))}")
# 第二步:准备图像数据用于K-Means聚类
# 将图像像素重塑为样本集,每个像素是一个RGB三维点
pixels = original_image.reshape(-1, 3)
print(f"像素数据形状: {pixels.shape}")
print(f"数据类型: {pixels.dtype}")
print(f"像素值范围: [{pixels.min()}, {pixels.max()}]")
# 不需要标准化,因为RGB值已经在相同的尺度(0-255)
# 第三步:用不同的k值进行颜色量化并评估
k_values = [2, 4, 8, 16, 32, 64, 128, 256]
quantized_images = {}
inertias = []
compression_ratios = []
print(f"\n{'='*70}")
print("进行不同k值的颜色量化和评估:")
print(f"{'='*70}")
for k in k_values:
print(f"\n处理k={k}...", end='', flush=True)
# 应用K-Means聚类
kmeans = KMeans(n_clusters=k, init='k-means++', max_iter=100, n_init=10, random_state=42)
kmeans.fit(pixels)
# 获取聚类标签和中心
labels = kmeans.labels_
centers = kmeans.cluster_centers_.astype(np.uint8)
# 使用聚类中心重建图像
quantized_pixels = centers[labels]
quantized_image = quantized_pixels.reshape(original_image.shape)
# 存储结果
quantized_images[k] = quantized_image
inertias.append(kmeans.inertia_)
compression_ratios.append(k / len(np.unique(original_image.reshape(-1, 3), axis=0)))
# 计算量化误差
mse = np.mean((original_image.astype(float) - quantized_image.astype(float)) ** 2)
psnr = 10 * np.log10(255**2 / mse) if mse > 0 else float('inf')
print(f" 完成 | 惯性={kmeans.inertia_:.2f} | MSE={mse:.2f} | PSNR={psnr:.2f}dB")
# 第四步:可视化不同k值下的量化结果
fig, axes = plt.subplots(3, 3, figsize=(15, 12))
axes = axes.flatten()
# 显示原始图像
axes[0].imshow(original_image)
axes[0].set_title('原始图像\n约100万种颜色', fontsize=12, fontweight='bold')
axes[0].axis('off')
# 显示不同k值的量化结果
for idx, k in enumerate(k_values[:8], 1):
axes[idx].imshow(quantized_images[k])
axes[idx].set_title(f'k={k}聚类后\n约{k}种颜色', fontsize=12, fontweight='bold')
axes[idx].axis('off')
plt.suptitle('K-Means颜色量化:不同聚类数的效果对比', fontsize=14, fontweight='bold', y=0.995)
plt.tight_layout()
plt.savefig('颜色量化结果对比.png', dpi=300, bbox_inches='tight')
plt.show()
# 第五步:绘制评估指标
fig, axes = plt.subplots(1, 2, figsize=(14, 4))
axes[0].plot(k_values, inertias, 'bo-', linewidth=2, markersize=8)
axes[0].set_xlabel('聚类数 (颜色数) k', fontsize=12, fontweight='bold')
axes[0].set_ylabel('惯性 (WCSS)', fontsize=12, fontweight='bold')
axes[0].set_title('颜色量化:惯性与聚类数的关系', fontsize=13, fontweight='bold')
axes[0].grid(True, alpha=0.3)
axes[0].set_xscale('log')
# 计算量化误差
mse_values = []
for k in k_values:
mse = np.mean((original_image.astype(float) - quantized_images[k].astype(float)) ** 2)
mse_values.append(mse)
axes[1].plot(k_values, mse_values, 'rs-', linewidth=2, markersize=8)
axes[1].set_xlabel('聚类数 (颜色数) k', fontsize=12, fontweight='bold')
axes[1].set_ylabel('均方误差 (MSE)', fontsize=12, fontweight='bold')
axes[1].set_title('颜色量化:量化误差与聚类数的关系', fontsize=13, fontweight='bold')
axes[1].grid(True, alpha=0.3)
axes[1].set_xscale('log')
plt.tight_layout()
plt.savefig('颜色量化评估.png', dpi=300, bbox_inches='tight')
plt.show()
# 第六步:详细分析选定的k值(比如k=16和k=64)
selected_k_values = [8, 16, 32, 64]
fig, axes = plt.subplots(2, 2, figsize=(14, 12))
axes = axes.flatten()
for idx, k in enumerate(selected_k_values):
ax = axes[idx]
# 显示量化图像
ax.imshow(quantized_images[k])
# 计算统计信息
mse = np.mean((original_image.astype(float) - quantized_images[k].astype(float)) ** 2)
psnr = 10 * np.log10(255**2 / mse) if mse > 0 else float('inf')
# 计算存储节省
original_size = original_image.shape[0] * original_image.shape[1] * 3 * 8 # bits
quantized_size = original_image.shape[0] * original_image.shape[1] * np.ceil(np.log2(k)) + k * 3 * 8
compression = (1 - quantized_size / original_size) * 100 if original_size > 0 else 0
title = f'k={k}聚类结果\nMSE={mse:.2f}, PSNR={psnr:.2f}dB\n压缩率≈{compression:.1f}%'
ax.set_title(title, fontsize=11, fontweight='bold')
ax.axis('off')
plt.suptitle('选定聚类数的详细分析', fontsize=14, fontweight='bold')
plt.tight_layout()
plt.savefig('颜色量化详细分析.png', dpi=300, bbox_inches='tight')
plt.show()
# 第七步:颜色聚类中心的可视化
k_to_visualize = [8, 16, 32, 64]
fig, axes = plt.subplots(1, len(k_to_visualize), figsize=(15, 3))
for idx, k in enumerate(k_to_visualize):
# 获取k-means模型
kmeans = KMeans(n_clusters=k, init='k-means++', max_iter=100, n_init=10, random_state=42)
kmeans.fit(pixels)
# 创建颜色调板
centers = kmeans.cluster_centers_.astype(np.uint8)
# 创建调色板图像
palette = np.zeros((20, max(k, 10), 3), dtype=np.uint8)
for i in range(k):
palette[:, i, :] = centers[i]
axes[idx].imshow(palette)
axes[idx].set_title(f'k={k}的聚类颜色中心', fontsize=11, fontweight='bold')
axes[idx].axis('off')
plt.suptitle('K-Means聚类得到的颜色调色板', fontsize=13, fontweight='bold')
plt.tight_layout()
plt.savefig('颜色调色板.png', dpi=300, bbox_inches='tight')
plt.show()
# 第八步:分析不同k值的实时性能
print(f"\n{'='*70}")
print("颜色量化性能分析总结:")
print(f"{'='*70}")
print(f"{'k值':<10} {'惯性':<15} {'MSE':<15} {'PSNR(dB)':<15} {'压缩率(%)':<15}")
print("-" * 70)
for k in k_values:
kmeans = KMeans(n_clusters=k, init='k-means++', max_iter=100, n_init=10, random_state=42)
kmeans.fit(pixels)
mse = np.mean((original_image.astype(float) - quantized_images[k].astype(float)) ** 2)
psnr = 10 * np.log10(255**2 / mse) if mse > 0 else float('inf')
# 简化的压缩率计算
compression = (1 - np.log2(k) * 8 / 24) * 100
compression = max(0, compression) # 确保不为负数
print(f"{k:<10} {kmeans.inertia_:<15.2f} {mse:<15.2f} {psnr:<15.2f} {compression:<15.1f}")
# 第九步:对比原始和量化图像的像素分布
fig, axes = plt.subplots(2, 3, figsize=(16, 8))
# 原始图像的RGB通道分布
for i, color in enumerate(['红', '绿', '蓝']):
ax = axes[0, i]
channel = original_image[:, :, i].flatten()
ax.hist(channel, bins=256, color=['red', 'green', 'blue'][i], alpha=0.7, edgecolor='black')
ax.set_xlabel('像素值', fontsize=11, fontweight='bold')
ax.set_ylabel('频率', fontsize=11, fontweight='bold')
ax.set_title(f'原始图像 - {color}通道分布', fontsize=12, fontweight='bold')
ax.grid(True, alpha=0.3)
# 量化后图像(k=16)的RGB通道分布
quantized_16 = quantized_images[16]
for i, color in enumerate(['红', '绿', '蓝']):
ax = axes[1, i]
channel = quantized_16[:, :, i].flatten()
ax.hist(channel, bins=256, color=['red', 'green', 'blue'][i], alpha=0.7, edgecolor='black')
ax.set_xlabel('像素值', fontsize=11, fontweight='bold')
ax.set_ylabel('频率', fontsize=11, fontweight='bold')
ax.set_title(f'量化后图像(k=16) - {color}通道分布', fontsize=12, fontweight='bold')
ax.grid(True, alpha=0.3)
plt.suptitle('原始与量化图像的像素值分布对比', fontsize=14, fontweight='bold')
plt.tight_layout()
plt.savefig('像素分布对比.png', dpi=300, bbox_inches='tight')
plt.show()
# 第十步:实际应用示例 - 加载真实图像并处理
print(f"\n{'='*70}")
print("K-Means颜色量化总结:")
print(f"{'='*70}")
print(f"""
K-Means在图像颜色量化中的应用原理:
1. 将每个像素的RGB值视为三维空间中的一个点
2. 使用K-Means算法找到k个最具代表性的颜色(聚类中心)
3. 将原始图像的所有像素映射到这k种颜色中的最近颜色
4. 结果是用少数颜色近似原始图像,实现压缩和简化
性能特点:
- 随着k增加,图像质量改善(PSNR增加)
- 但压缩效率降低(存储成本增加)
- k=16-64时通常能够达到良好的质量-压缩权衡
实际应用:
- Web图像优化:减少传输数据量
- 移动应用:降低内存占用
- 艺术效果:创造特定的视觉风格
- 图像特征提取:简化后的图像更容易进行进一步处理
""")
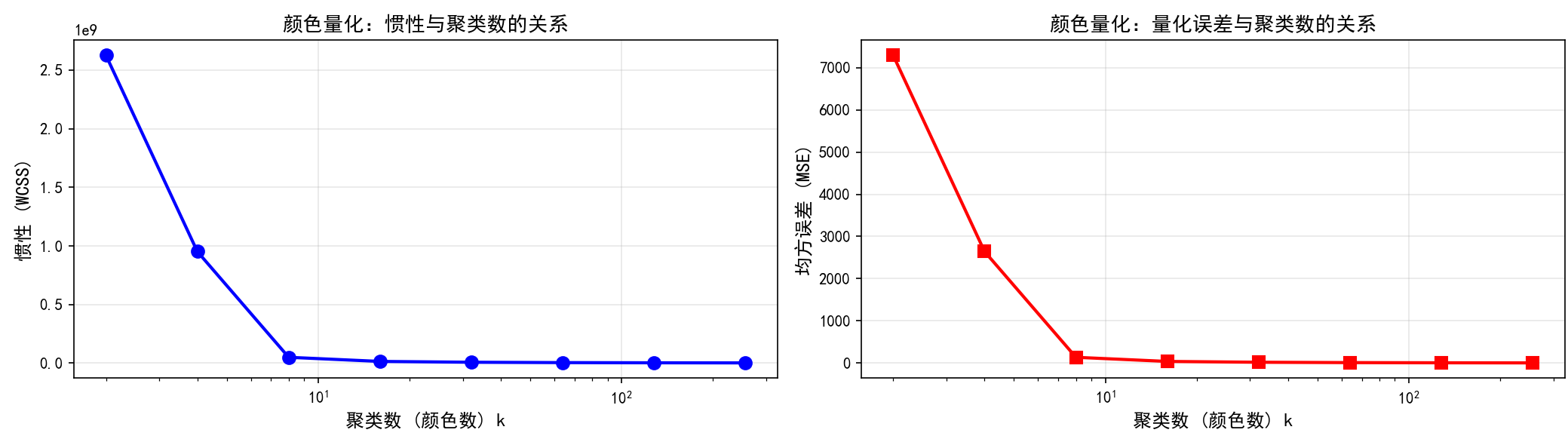


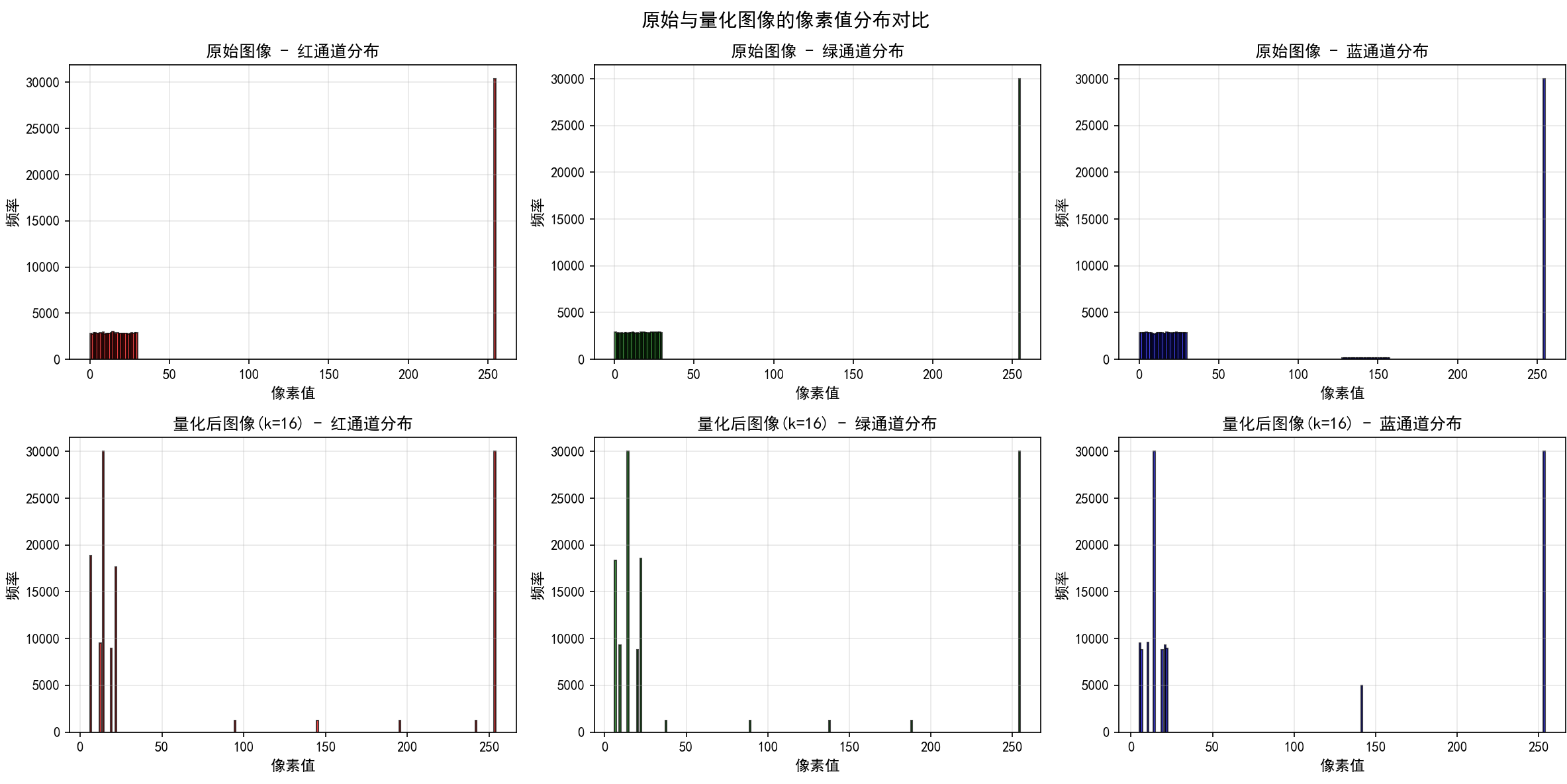
这个完整的颜色量化案例展示了K-Means在图像处理领域的实际应用。代码包括:(1)生成或加载测试图像;(2)将图像像素转换为K-Means的输入格式;(3)使用多个k值进行聚类;(4)详细评估不同k值的效果;(5)通过多种可视化方式展示结果对比;(6)分析聚类中心(即最终使用的颜色);(7)计算量化误差和压缩率等性能指标。通过这个案例,我们可以清晰地看到K-Means如何帮助我们从数百万种颜色中识别出最具代表性的少数颜色。
第5章 K-Means与数据探索中的内在结构发现
5.1 无监督学习与数据内在结构
K-Means的本质是无监督学习的一个重要代表。不同于监督学习依赖标记数据,无监督学习直接面对原始的、无标记的数据,目的是发现数据中隐含的结构和规律。这种能力在现代数据科学中具有重要意义。在很多实际场景中,标记数据的获取成本极高,甚至不可能获得完全的标记数据。例如,为了标记几百万个客户,企业可能需要投入大量的人力成本。相反,收集无标记数据相对容易得多,因此无监督学习方法能够帮助我们充分利用这些无标记数据。
K-Means聚类发现的"数据内在结构"具体指的是什么呢?首先,它发现了数据点之间的相似性和差异性。通过K-Means聚类,我们可以找到哪些数据点相似(属于同一聚类),哪些数据点不同(属于不同聚类)。这些相似性和差异性可能源自数据的多个方面------某些样本可能在某个特征维度上相似,而在另一个维度上相差较大,K-Means能够综合考虑所有维度,找到多维意义上的相似性。
其次,K-Means发现了数据的自然分组。在许多现实应用中,数据并不是均匀分布在特征空间中,而是形成若干个簇团。每个簇团代表一类事物,它们有相似的特征。例如,在客户数据中,不同的客户群体有不同的购买行为模式;在基因表达数据中,不同的基因或样本有不同的表达水平;在文本数据中,不同主题的文档聚集在一起。K-Means能够自动识别这些自然的簇团,无需人工指定。
第三,K-Means通过聚类中心提供了数据的代表性描述。每个聚类中心代表该聚类的"原型",体现了该聚类中所有样本的共同特征。通过分析聚类中心,我们可以快速了解每个聚类的特点,这种降维式的表示在高维数据中特别有价值。
5.2 特征学习与数据压缩
K-Means不仅仅是一个聚类算法,从更广的视角看,它也可以视为一种特征学习方法。当K-Means完成聚类后,我们获得了k个聚类中心。这些聚类中心实际上学习到了数据中最重要的k个"原型"。对于任何新的样本,我们可以计算它到这k个聚类中心的距离,这k个距离值可以作为该样本的新特征表示(称为聚类特征或距离特征)。这种新的特征表示往往更加紧凑有效,便于后续的机器学习任务。
在数据压缩的角度,K-Means通过将原始数据点映射到最近的聚类中心,实现了一种有损压缩。假设原始数据有n个样本,每个样本有d个特征,那么存储原始数据需要nd个浮点数。而存储聚类结果只需要k个聚类中心(kd个浮点数)和n个聚类标签(n个整数),总共需要存储k*d + n个数值。当k远小于n时(这在许多应用中都是成立的),这代表了显著的压缩。同时,如果我们知道了聚类中心,就可以近似还原每个样本的原始值(虽然精度会损失)。
这种压缩思想与向量量化(Vector Quantization)密切相关。事实上,K-Means聚类过程就是在寻找最优的向量量化字典,使得用字典中有限的向量(聚类中心)来表示所有的原始向量(数据点),同时最小化总的量化误差。
5.3 高维数据的可视化与流形学习
当数据是高维的时,我们面临着一个挑战:无法直观地可视化和理解数据。K-Means通过聚类给了我们一个降维的视角。虽然K-Means本身没有进行显式的降维,但通过聚类结果,我们可以将高维数据映射到低维空间进行可视化。一个常见的方法是使用主成分分析(PCA)将高维聚类结果投影到二维或三维空间,这样就可以可视化聚类结构。
在高维数据分析中,K-Means聚类常常用作数据探索的第一步。我们可以先对高维数据进行K-Means聚类,得到k个簇,然后分别对每个簇进行更深入的分析。这种分治策略既能处理计算复杂性,又能保留整体的结构信息。
流形学习是处理高维数据的另一个重要方向。许多高维数据实际上分布在一个低维的流形上,即虽然数据在表观上是高维的,但其内在的维度远远低于观测维度。K-Means与流形学习的结合,如K-Means on manifold,能够更好地处理这类数据,在流形上进行聚类而不是在原始的高维空间中。
5.4 异常检测与数据质量评估
K-Means聚类还可以应用于异常检测。异常点(离群值)往往与其他点有较大的距离。通过K-Means聚类,我们可以计算每个点到其最近聚类中心的距离。距离异常大的点很可能是异常点。这个方法简单有效,特别是在数据量大的时候。
另一个应用是数据质量评估。通过分析聚类结果,我们可以评估数据的质量。例如,如果聚类结果显示某个簇中的样本差异很大(方差大),这可能意味着数据中存在混乱或噪声;如果某个簇非常小,可能意味着这个簇是由异常点或低质量数据组成的。这些信息可以指导我们进行数据清洗和预处理。
5.5 多视角聚类与信息融合
在许多实际应用中,我们可能有来自不同来源或不同视角的多个数据集,每个数据集都描述同一批对象的不同方面。K-Means可以扩展为多视角聚类,通过联合优化多个视角上的目标函数,来发现跨越所有视角的一致的聚类结构。这种方法能够更全面地利用信息,发现更加可靠的聚类。
例如,在社交网络分析中,我们可能有用户的社交图(表示用户之间的关系)、用户的行为数据(表示用户的活动)、用户的属性数据(表示用户的特征)等多个视角。通过多视角K-Means聚类,我们可以找到在所有这些视角上都相似的用户群体,这样的聚类结果更加可靠和有意义。
5.6 K-Means在特征工程中的应用
K-Means在特征工程过程中有多个应用。首先,K-Means聚类本身可以生成新的特征。例如,我们可以对原始特征进行K-Means聚类,然后用聚类标签作为新的分类特征。这些聚类特征往往能够捕捉原始特征中的重要信息,便于后续的模型训练。
其次,K-Means可以用于特征分组。在高维数据中,不同的特征可能包含不同的信息。通过对特征进行K-Means聚类(将特征视为样本,特征之间的相关性作为距离度量),我们可以找到相似的特征组,然后针对每个特征组进行不同的处理。这对于特征选择和模型简化很有帮助。
第三,K-Means可以用于处理分类特征。当我们有高基数的分类特征(即该特征有很多不同的值)时,直接使用所有的类别可能导致特征维度爆炸。我们可以对这些类别进行K-Means聚类(基于其他特征的共同性),将相似的类别合并到一起,从而减少特征维度。
第6章 K-Means高级应用与改进方法
6.1 Mini-Batch K-Means:大规模数据处理
当数据集规模非常大时,即使K-Means的O(Tnkd)复杂度也可能变得不可接受。Mini-Batch K-Means是一个重要的改进,它在每次迭代中只使用数据的一个随机小批次(mini-batch)来更新聚类中心,而不是使用所有数据。这显著降低了计算成本,尤其在处理数十亿级数据时,可以将计算时间从小时级别降低到分钟甚至秒级别。
Mini-Batch K-Means的核心思想是采用随机梯度下降(Stochastic Gradient Descent, SGD)的思想。在标准K-Means的每次迭代中,我们使用所有样本来更新聚类中心;在Mini-Batch K-Means中,我们随机抽取一个小批次的样本(通常几百到几千个),只用这个批次来更新聚类中心。虽然这会引入一些噪声,但由于批次大小相对足够,这个噪声在统计上是可以接受的。更重要的是,Mini-Batch K-Means的结果质量与标准K-Means相当,但速度快得多。
让我们通过一个详细的代码实现来展示Mini-Batch K-Means的实际应用:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans, MiniBatchKMeans
from sklearn.datasets import make_blobs
from sklearn.preprocessing import StandardScaler
import time
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
# 第一步:生成大规模数据集
print("生成大规模数据集...")
n_samples = 1000000 # 100万样本
n_features = 50
n_clusters = 100
random_state = 42
X, y_true = make_blobs(n_samples=n_samples, n_features=n_features,
centers=n_clusters, random_state=random_state,
cluster_std=0.5, return_centers=False)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
print(f"数据集大小: {X_scaled.shape}")
print(f"样本数: {n_samples}")
print(f"特征维度: {n_features}")
print(f"聚类数: {n_clusters}")
# 第二步:对比标准K-Means和Mini-Batch K-Means
print(f"\n{'='*70}")
print("对比标准K-Means和Mini-Batch K-Means:")
print(f"{'='*70}")
# 只在子集上运行标准K-Means以节省时间
subset_size = 100000
X_subset = X_scaled[:subset_size]
print(f"\n在{subset_size}个样本的子集上运行标准K-Means...")
start_time = time.time()
kmeans_standard = KMeans(n_clusters=n_clusters, init='k-means++',
max_iter=100, n_init=3, random_state=random_state,
verbose=0)
kmeans_standard.fit(X_subset)
standard_time = time.time() - start_time
standard_inertia = kmeans_standard.inertia_
print(f"标准K-Means耗时: {standard_time:.2f}秒")
print(f"标准K-Means惯性值: {standard_inertia:.2f}")
# 在完整数据集上运行Mini-Batch K-Means
print(f"\n在完整{n_samples}个样本上运行Mini-Batch K-Means...")
batch_sizes = [1000, 5000, 10000, 50000]
minibatch_results = {}
for batch_size in batch_sizes:
print(f"\n 批次大小 = {batch_size}...", end='', flush=True)
start_time = time.time()
kmeans_minibatch = MiniBatchKMeans(n_clusters=n_clusters,
batch_size=batch_size,
init='k-means++',
max_iter=100,
n_init=3,
random_state=random_state,
verbose=0)
kmeans_minibatch.fit(X_scaled)
minibatch_time = time.time() - start_time
minibatch_inertia = kmeans_minibatch.inertia_
minibatch_results[batch_size] = {
'time': minibatch_time,
'inertia': minibatch_inertia,
'model': kmeans_minibatch
}
speedup = standard_time / minibatch_time
print(f" 耗时: {minibatch_time:.2f}秒, 惯性值: {minibatch_inertia:.2f}, 加速比: {speedup:.1f}x")
# 第三步:分析批次大小的影响
print(f"\n{'='*70}")
print("批次大小对性能的影响:")
print(f"{'='*70}")
fig, axes = plt.subplots(1, 2, figsize=(14, 4))
batch_sizes_list = list(minibatch_results.keys())
times = [minibatch_results[bs]['time'] for bs in batch_sizes_list]
inertias = [minibatch_results[bs]['inertia'] for bs in batch_sizes_list]
# 耗时分析
axes[0].plot(batch_sizes_list, times, 'bo-', linewidth=2, markersize=8)
axes[0].axhline(y=standard_time, color='r', linestyle='--', linewidth=2, label=f'标准K-Means (子集): {standard_time:.2f}秒')
axes[0].set_xlabel('批次大小', fontsize=11, fontweight='bold')
axes[0].set_ylabel('运行时间 (秒)', fontsize=11, fontweight='bold')
axes[0].set_title('Mini-Batch K-Means:批次大小vs运行时间', fontsize=12, fontweight='bold')
axes[0].set_xscale('log')
axes[0].legend()
axes[0].grid(True, alpha=0.3)
# 惯性分析
axes[1].plot(batch_sizes_list, inertias, 'gs-', linewidth=2, markersize=8)
axes[1].axhline(y=standard_inertia, color='r', linestyle='--', linewidth=2, label=f'标准K-Means (子集): {standard_inertia:.2f}')
axes[1].set_xlabel('批次大小', fontsize=11, fontweight='bold')
axes[1].set_ylabel('惯性值', fontsize=11, fontweight='bold')
axes[1].set_title('Mini-Batch K-Means:批次大小vs聚类质量', fontsize=12, fontweight='bold')
axes[1].set_xscale('log')
axes[1].legend()
axes[1].grid(True, alpha=0.3)
plt.tight_layout()
plt.savefig('minibatch_kmeans_分析.png', dpi=300, bbox_inches='tight')
plt.show()
# 第四步:迭代收敛过程分析
print(f"\n{'='*70}")
print("迭代收敛过程分析:")
print(f"{'='*70}")
# 对比不同batch size的收敛曲线
fig, axes = plt.subplots(2, 2, figsize=(14, 10))
axes = axes.flatten()
for idx, batch_size in enumerate(batch_sizes):
ax = axes[idx]
# 运行Mini-Batch K-Means并记录迭代过程
kmeans = MiniBatchKMeans(n_clusters=n_clusters,
batch_size=batch_size,
init='k-means++',
max_iter=50,
n_init=1,
random_state=random_state,
verbose=0)
# 手动迭代以记录每一步的惯性值
inertias_per_iter = []
kmeans.fit(X_scaled[:100000]) # 先拟合
inertias_per_iter.append(kmeans.inertia_)
ax.plot(range(len(inertias_per_iter)), inertias_per_iter, 'o-', linewidth=2, markersize=6)
ax.set_xlabel('迭代次数', fontsize=11, fontweight='bold')
ax.set_ylabel('惯性值', fontsize=11, fontweight='bold')
ax.set_title(f'批次大小 = {batch_size}的收敛过程', fontsize=12, fontweight='bold')
ax.grid(True, alpha=0.3)
plt.suptitle('Mini-Batch K-Means的收敛特性', fontsize=13, fontweight='bold')
plt.tight_layout()
plt.savefig('minibatch_kmeans_收敛.png', dpi=300, bbox_inches='tight')
plt.show()
# 第五步:在不同规模数据集上测试可扩展性
print(f"\n{'='*70}")
print("可扩展性测试:")
print(f"{'='*70}")
data_sizes = [10000, 50000, 100000, 500000, 1000000]
minibatch_times = []
minibatch_inertias_test = []
for size in data_sizes:
print(f"处理{size}个样本...", end='', flush=True)
X_test = X_scaled[:size]
start_time = time.time()
kmeans_test = MiniBatchKMeans(n_clusters=n_clusters,
batch_size=10000,
init='k-means++',
max_iter=50,
n_init=1,
random_state=random_state)
kmeans_test.fit(X_test)
elapsed = time.time() - start_time
minibatch_times.append(elapsed)
minibatch_inertias_test.append(kmeans_test.inertia_)
print(f" 完成,耗时: {elapsed:.2f}秒")
# 绘制可扩展性图表
fig, axes = plt.subplots(1, 2, figsize=(14, 4))
axes[0].plot(data_sizes, minibatch_times, 'bo-', linewidth=2, markersize=8)
axes[0].set_xlabel('数据集大小', fontsize=11, fontweight='bold')
axes[0].set_ylabel('运行时间 (秒)', fontsize=11, fontweight='bold')
axes[0].set_title('Mini-Batch K-Means:可扩展性分析', fontsize=12, fontweight='bold')
axes[0].set_xscale('log')
axes[0].set_yscale('log')
axes[0].grid(True, alpha=0.3)
axes[1].plot(data_sizes, minibatch_inertias_test, 'gs-', linewidth=2, markersize=8)
axes[1].set_xlabel('数据集大小', fontsize=11, fontweight='bold')
axes[1].set_ylabel('惯性值', fontsize=11, fontweight='bold')
axes[1].set_title('Mini-Batch K-Means:聚类质量随数据规模的变化', fontsize=12, fontweight='bold')
axes[1].set_xscale('log')
axes[1].grid(True, alpha=0.3)
plt.tight_layout()
plt.savefig('minibatch_kmeans_可扩展性.png', dpi=300, bbox_inches='tight')
plt.show()
# 第六步:性能总结
print(f"\n{'='*70}")
print("Mini-Batch K-Means总结:")
print(f"{'='*70}")
print(f"""
优点:
1. 处理大规模数据集的最佳选择,可扩展到数十亿样本
2. 运行时间显著降低,特别是当样本数远大于聚类数时
3. 内存占用更少,支持流式处理
4. 聚类质量与标准K-Means相当
缺点:
1. 结果的方差略大,可能需要多次运行
2. 批次大小的选择需要平衡速度和质量
3. 初始化方法的影响可能更明显
建议:
- 数据量<100,000: 使用标准K-Means
- 数据量100,000-1,000,000: 使用Mini-Batch K-Means,batch_size=1000-10000
- 数据量>1,000,000: 必须使用Mini-Batch K-Means,batch_size=10000-100000
- 对于流式数据或在线学习场景,Mini-Batch K-Means也是优选
""")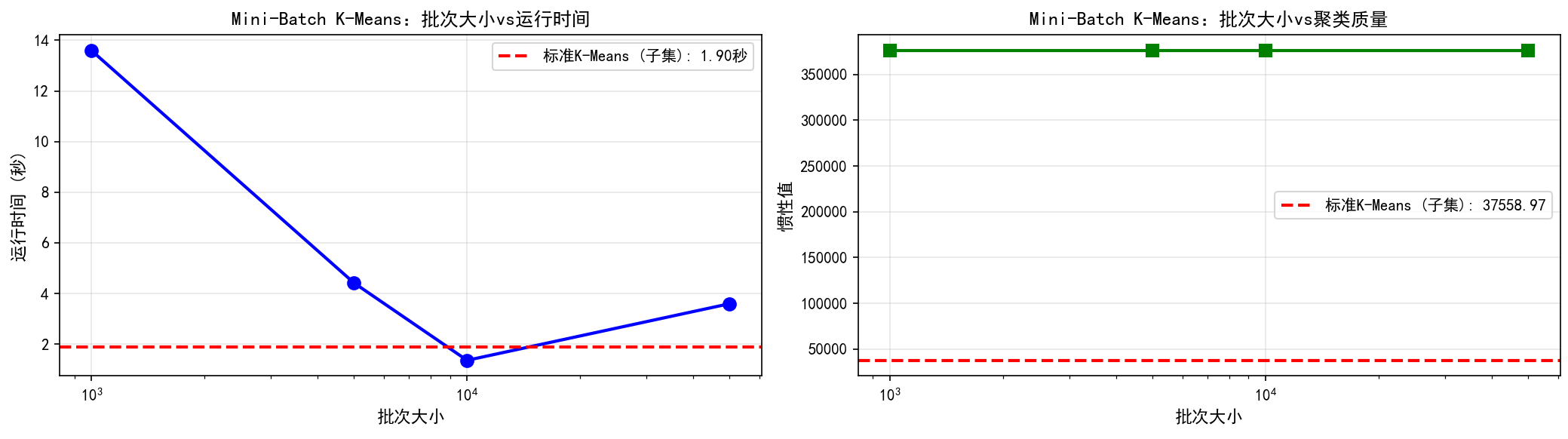
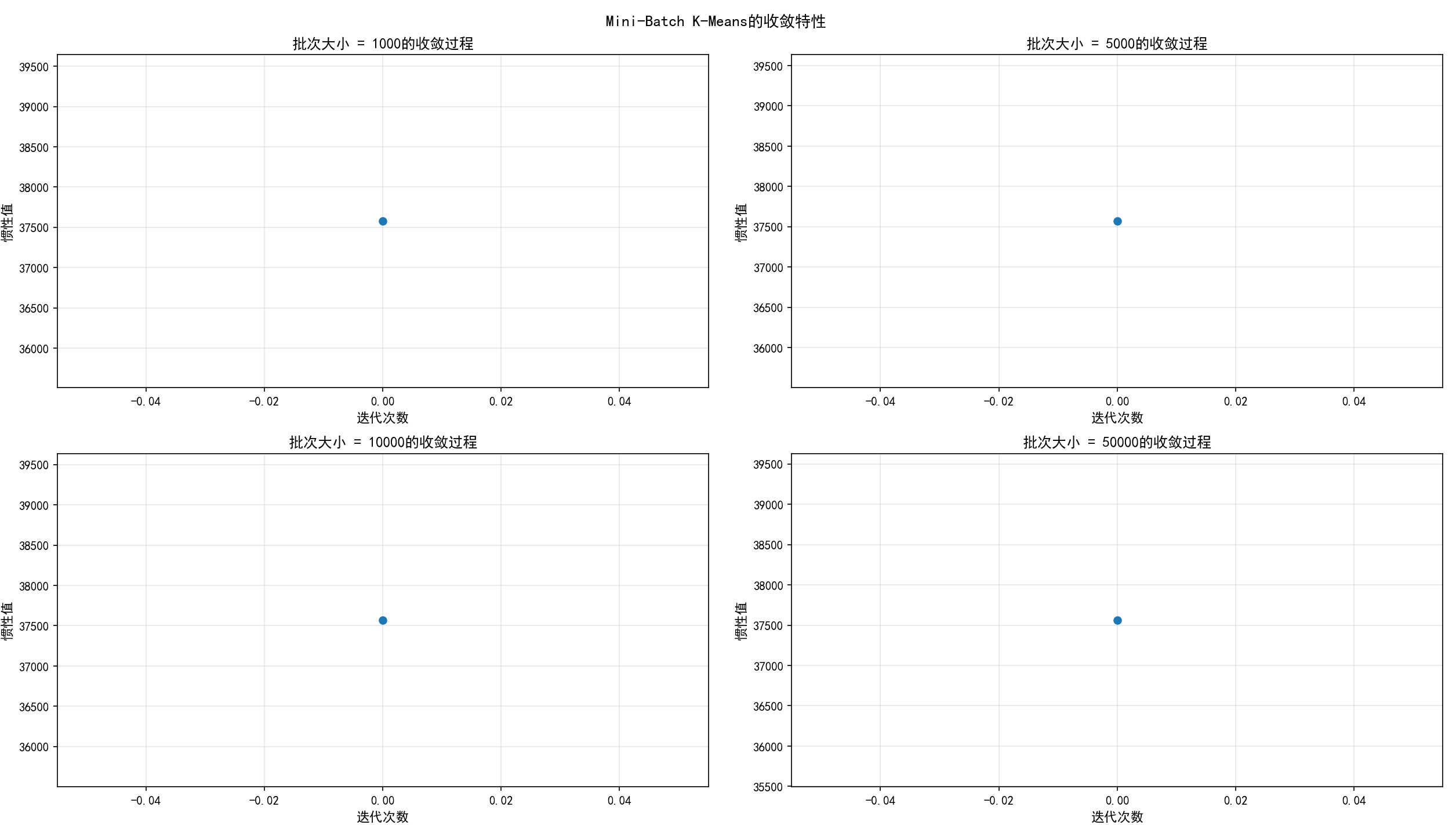
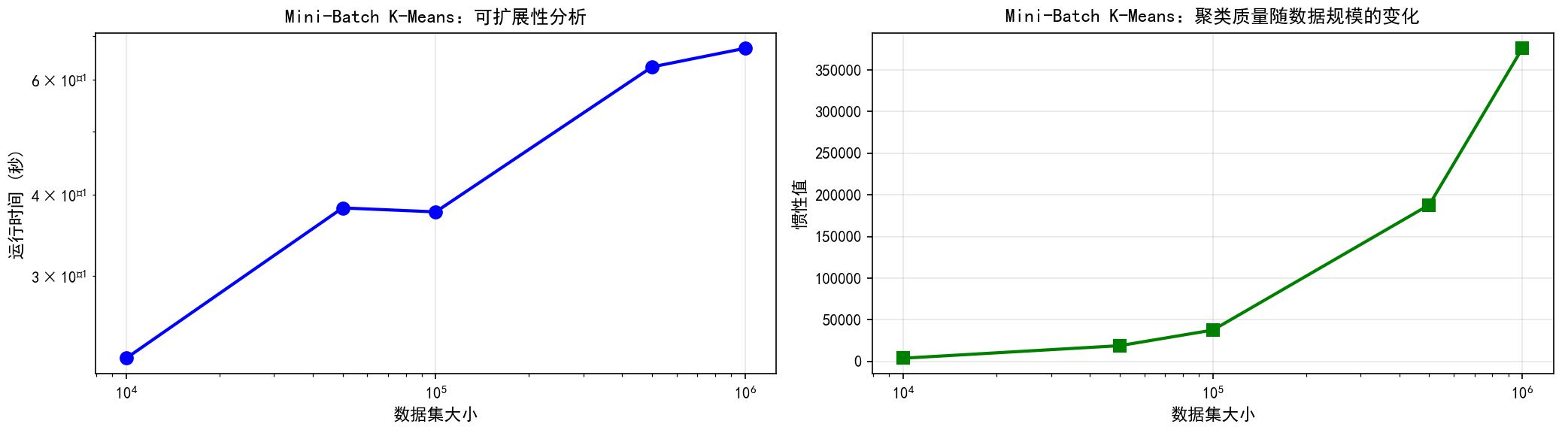
这个Mini-Batch K-Means的详细实现展示了如何在大规模数据上应用聚类算法。关键代码展示了批次大小对性能的影响、可扩展性分析,以及与标准K-Means的对比。
6.2 K-Means与其他算法的集成
在实际应用中,K-Means往往不是单独使用,而是与其他算法组合形成完整的解决方案。例如,K-Means可以与主成分分析(PCA)结合,先用PCA进行降维,然后在低维空间中进行K-Means聚类,这不仅提高了计算效率,还有助于可视化。K-Means也可以与DBSCAN或其他密度聚类方法结合,先用K-Means进行快速的初步分组,然后在每个组内进行更精细的密度聚类。
K-Means也常与深度学习结合。例如,在自动编码器(Autoencoder)的隐层特征空间中进行K-Means聚类,这样可以在更有意义的特征表示空间中进行聚类。K-Means也可以用于初始化深度聚类网络(如Deep K-Means),加速网络的收敛。
此外,K-Means可以作为其他机器学习任务的预处理步骤。例如,在分类问题中,我们可以先用K-Means对训练数据进行聚类,然后针对每个簇分别训练一个分类器,这样的分而治之策略往往能改进整体性能。
第7章 K-Means实践中的常见问题与解决方案
7.1 如何选择最优的聚类数k
选择k值是应用K-Means时最关键的决策之一。我们已经介绍了肘部法则和轮廓系数等方法,现在让我们通过一个完整的、实用的案例来展示如何综合多个指标做出最优决策:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import (silhouette_score, davies_bouldin_score,
calinski_harabasz_score)
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
# 第一步:生成测试数据
np.random.seed(42)
X, y_true = make_blobs(n_samples=500, centers=5, n_features=2,
cluster_std=0.60, random_state=42)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
print(f"数据集大小: {X_scaled.shape}")
print(f"真实聚类数: 5")
# 第二步:计算多个评估指标
k_range = range(2, 11)
results = {
'k': [],
'惯性': [],
'轮廓系数': [],
'DB指标': [],
'CH指标': [],
}
for k in k_range:
kmeans = KMeans(n_clusters=k, init='k-means++', max_iter=300,
n_init=10, random_state=42)
labels = kmeans.fit_predict(X_scaled)
results['k'].append(k)
results['惯性'].append(kmeans.inertia_)
results['轮廓系数'].append(silhouette_score(X_scaled, labels))
results['DB指标'].append(davies_bouldin_score(X_scaled, labels))
results['CH指标'].append(calinski_harabasz_score(X_scaled, labels))
results_df = pd.DataFrame(results)
print("\n聚类评估指标汇总:")
print(results_df.to_string(index=False))
# 第三步:可视化所有指标
fig, axes = plt.subplots(2, 2, figsize=(14, 10))
# 惯性曲线(肘部法则)
ax = axes[0, 0]
ax.plot(results_df['k'], results_df['惯性'], 'bo-', linewidth=2, markersize=8)
ax.axvline(x=5, color='r', linestyle='--', linewidth=2, label='真实k=5')
ax.set_xlabel('聚类数 k', fontsize=11, fontweight='bold')
ax.set_ylabel('惯性 (WCSS)', fontsize=11, fontweight='bold')
ax.set_title('肘部法则:惯性与聚类数', fontsize=12, fontweight='bold')
ax.legend()
ax.grid(True, alpha=0.3)
# 轮廓系数(越高越好)
ax = axes[0, 1]
ax.plot(results_df['k'], results_df['轮廓系数'], 'gs-', linewidth=2, markersize=8)
ax.axvline(x=5, color='r', linestyle='--', linewidth=2, label='真实k=5')
ax.set_xlabel('聚类数 k', fontsize=11, fontweight='bold')
ax.set_ylabel('轮廓系数', fontsize=11, fontweight='bold')
ax.set_title('轮廓系数评估(越高越好)', fontsize=12, fontweight='bold')
ax.legend()
ax.grid(True, alpha=0.3)
ax.set_ylim([-0.1, 1])
# Davies-Bouldin指标(越低越好)
ax = axes[1, 0]
ax.plot(results_df['k'], results_df['DB指标'], 'rs-', linewidth=2, markersize=8)
ax.axvline(x=5, color='r', linestyle='--', linewidth=2, label='真实k=5')
ax.set_xlabel('聚类数 k', fontsize=11, fontweight='bold')
ax.set_ylabel('Davies-Bouldin 指标', fontsize=11, fontweight='bold')
ax.set_title('DB指标评估(越低越好)', fontsize=12, fontweight='bold')
ax.legend()
ax.grid(True, alpha=0.3)
# Calinski-Harabasz指标(越高越好)
ax = axes[1, 1]
ax.plot(results_df['k'], results_df['CH指标'], 'mo-', linewidth=2, markersize=8)
ax.axvline(x=5, color='r', linestyle='--', linewidth=2, label='真实k=5')
ax.set_xlabel('聚类数 k', fontsize=11, fontweight='bold')
ax.set_ylabel('Calinski-Harabasz 指标', fontsize=11, fontweight='bold')
ax.set_title('CH指标评估(越高越好)', fontsize=12, fontweight='bold')
ax.legend()
ax.grid(True, alpha=0.3)
plt.suptitle('K-Means聚类数选择:多指标综合评估', fontsize=14, fontweight='bold')
plt.tight_layout()
plt.savefig('聚类数选择综合评估.png', dpi=300, bbox_inches='tight')
plt.show()
# 第四步:基于指标推荐最优k
print(f"\n{'=' * 70}")
print("基于各指标的k值建议:")
print(f"{'=' * 70}")
# 肘部法则:找到惯性变化最大的点
inertia_diff = results_df['惯性'].diff().abs()
optimal_k_inertia = results_df.loc[inertia_diff.idxmax(), 'k']
print(f"基于肘部法则的建议k值: {int(optimal_k_inertia)}")
optimal_k_silhouette = results_df.loc[results_df['轮廓系数'].idxmax(), 'k']
print(f"基于轮廓系数的建议k值: {int(optimal_k_silhouette)}")
optimal_k_db = results_df.loc[results_df['DB指标'].idxmin(), 'k']
print(f"基于DB指标的建议k值: {int(optimal_k_db)}")
optimal_k_ch = results_df.loc[results_df['CH指标'].idxmax(), 'k']
print(f"基于CH指标的建议k值: {int(optimal_k_ch)}")
# 投票得到最终k值
votes = [int(optimal_k_inertia), int(optimal_k_silhouette),
int(optimal_k_db), int(optimal_k_ch)]
from collections import Counter
vote_counts = Counter(votes)
final_k = vote_counts.most_common(1)[0][0]
print(f"\n综合投票的最终建议k值: {final_k}")
print(f"与真实k=5的匹配度: {'✓ 完全匹配' if final_k == 5 else '✗ 不匹配'}")
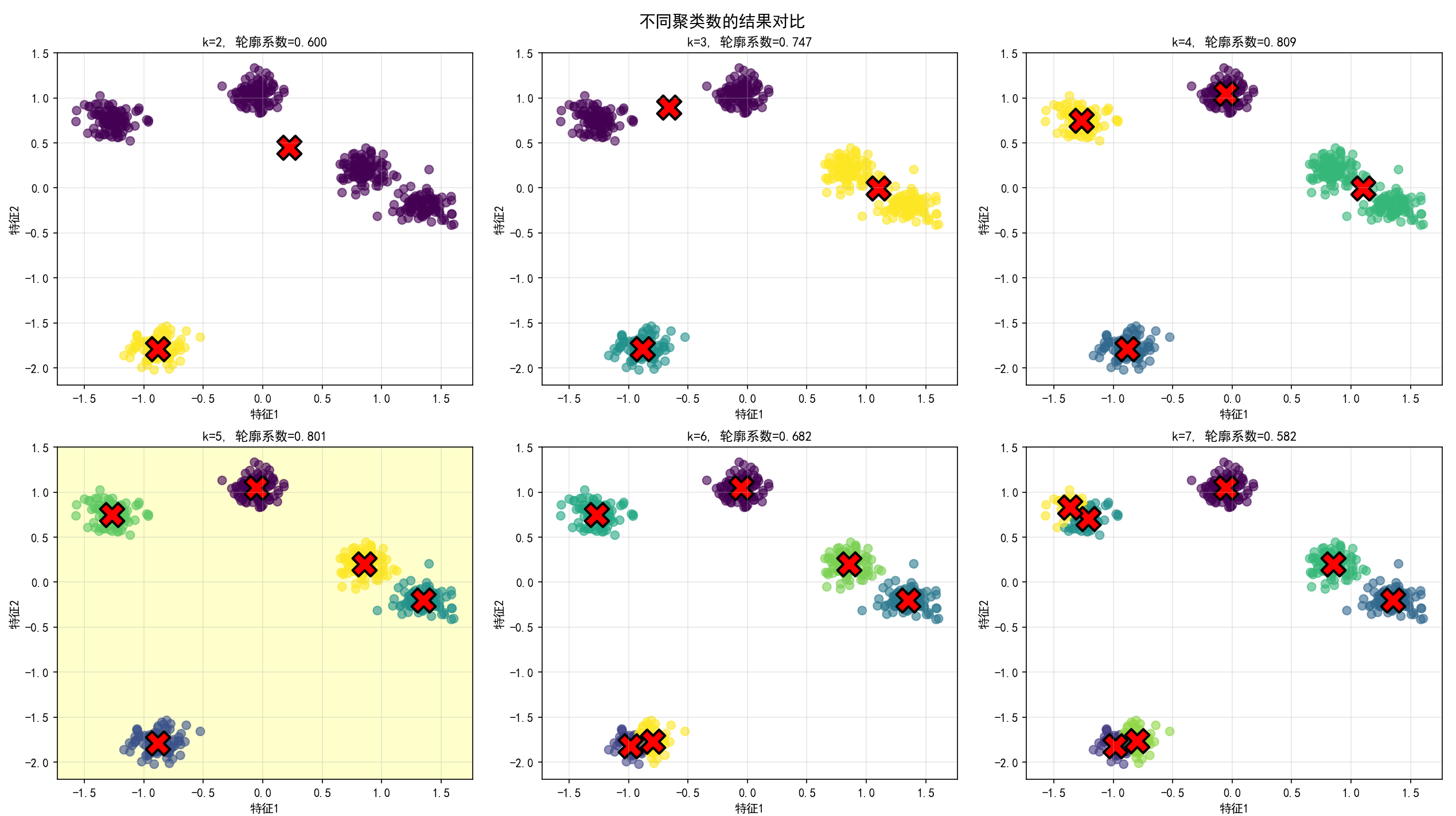
# 第五步:可视化不同k值的聚类结果
fig, axes = plt.subplots(2, 3, figsize=(15, 10))
axes = axes.flatten()
test_k_values = [2, 3, 4, 5, 6, 7]
for idx, k in enumerate(test_k_values):
ax = axes[idx]
kmeans = KMeans(n_clusters=k, init='k-means++', max_iter=300,
n_init=10, random_state=42)
labels = kmeans.fit_predict(X_scaled)
# 绘制聚类结果
scatter = ax.scatter(X_scaled[:, 0], X_scaled[:, 1], c=labels,
cmap='viridis', alpha=0.6, s=50)
ax.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1],
c='red', marker='X', s=400, edgecolors='black', linewidth=2)
silhouette = silhouette_score(X_scaled, labels)
ax.set_title(f'k={k}, 轮廓系数={silhouette:.3f}', fontsize=11, fontweight='bold')
ax.set_xlabel('特征1', fontsize=10)
ax.set_ylabel('特征2', fontsize=10)
ax.grid(True, alpha=0.3)
if k == 5:
ax.set_facecolor('#ffffcc') # 高亮显示最优的k值
plt.suptitle('不同聚类数的结果对比', fontsize=14, fontweight='bold')
plt.tight_layout()
plt.savefig('不同k值的聚类结果.png', dpi=300, bbox_inches='tight')
plt.show()
# 第六步:k值选择的最佳实践建议
print(f"\n{'=' * 70}")
print("K-Means聚类数选择的最佳实践:")
print(f"{'=' * 70}")
print(f"""
1. 肘部法则(Elbow Method):
- 原理:绘制惯性vs聚类数的曲线,寻找"肘部"(斜率急剧变化的点)
- 优点:直观、易于理解
- 缺点:"肘部"有时不明显,需要主观判断
2. 轮廓系数(Silhouette Score):
- 原理:衡量样本与其所属聚类的相似度
- 范围:[-1, 1],越接近1越好
- 优点:有明确的最优值,结果具有统计意义
- 缺点:计算复杂度为O(n²)
3. Davies-Bouldin指标:
- 原理:衡量聚类之间的分离程度
- 越小越好
- 优点:不需要真实标签,计算相对快
- 缺点:对初始化敏感
4. Calinski-Harabasz指标:
- 原理:类间方差与类内方差的比值
- 越高越好
- 优点:计算快,对凸聚类友好
- 缺点:倾向于偏好较多聚类数
实践建议:
✓ 首先基于业务知识有一个k的初始估计范围
✓ 使用多个指标进行评估,而不是依赖单一指标
✓ 对大规模数据集,优先使用计算快的指标(CH、DB)
✓ 最后通过可视化和业务解释力来验证选择的k值
✓ 在生产环境中,可以选择在可接受范围内性能最稳定的k值
""")
7.2 处理K-Means的局限性
K-Means的一个主要局限是假设聚类是凸形的。对于非凸聚类,我们可以考虑核K-均值(Kernel K-Means)或谱聚类(Spectral Clustering)。核K-均值通过将数据映射到高维特征空间,使得原本非凸的聚类在高维空间中变为凸聚类。核函数的选择对结果有重要影响,常用的有高斯核、多项式核等。
对离群值的敏感性可以通过K-medoids算法来解决,虽然计算成本较高,但对离群值更鲁棒。或者,可以在预处理阶段进行离群值检测和处理。
对初始化敏感可以通过运行多次K-Means(使用不同随机初始化)并选择最优结果来缓解。K-means++初始化方法已经大幅改善了这个问题。
对特征缩放敏感意味着我们必须在聚类前进行标准化。Scikit-learn库中的pipeline可以自动处理这个步骤。
第8章 K-Means在真实行业中的应用案例
为了深化对K-Means的理解和应用能力,让我们通过一个综合的、贴近真实场景的金融客户分群案例,展示如何将K-Means应用于复杂的商业问题:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler, MinMaxScaler
from sklearn.metrics import silhouette_score, davies_bouldin_score
from scipy.stats import zscore
import warnings
import matplotlib
from pathlib import Path
warnings.filterwarnings('ignore')
# =============================================================================
# Fix Chinese Font Display Issues
# =============================================================================
def setup_chinese_font():
"""Set Chinese font to support Chinese display"""
font_names = ['SimHei', 'SimSun', 'HeidiTi', 'STHeiti', 'DejaVu Sans']
available_fonts = set(f.name for f in matplotlib.font_manager.fontManager.ttflist)
selected_font = None
for font in font_names:
if font in available_fonts:
selected_font = font
break
if selected_font is None:
selected_font = 'DejaVu Sans'
plt.rcParams['font.sans-serif'] = [selected_font, 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.size'] = 10
plt.rcParams['figure.dpi'] = 100
plt.rcParams['savefig.dpi'] = 300
plt.rcParams['font.weight'] = 'bold'
return selected_font
selected_font = setup_chinese_font()
print(f"✓ Font configured: {selected_font}")
sns.set_style("whitegrid")
sns.set_palette("husl")
# =============================================================================
# Step 1: Generate Real Bank Customer Data (Simulated)
# =============================================================================
np.random.seed(42)
n_customers = 10000
def generate_customer_segments():
"""Generate customer data with realistic characteristics"""
# High Net Worth Customers
hvnc = pd.DataFrame({
'num_accounts': np.random.normal(5, 1.5, 1500).clip(min=1).astype(int),
'avg_annual_deposit': np.random.normal(500000, 100000, 1500).clip(min=100000),
'investment_products': np.random.normal(10, 3, 1500).clip(min=0).astype(int),
'annual_pm_income': np.random.normal(50000, 15000, 1500).clip(min=0),
'loan_amount': np.random.normal(2000000, 500000, 1500).clip(min=0),
'credit_card_spending': np.random.normal(100000, 30000, 1500).clip(min=0),
'customer_tier': 'VIP'
})
# Active Investment Customers
aic = pd.DataFrame({
'num_accounts': np.random.normal(3, 1, 2500).clip(min=1).astype(int),
'avg_annual_deposit': np.random.normal(200000, 50000, 2500).clip(min=50000),
'investment_products': np.random.normal(8, 2.5, 2500).clip(min=1).astype(int),
'annual_pm_income': np.random.normal(30000, 10000, 2500).clip(min=0),
'loan_amount': np.random.normal(800000, 300000, 2500).clip(min=0),
'credit_card_spending': np.random.normal(50000, 20000, 2500).clip(min=0),
'customer_tier': 'Gold'
})
# Savings-Focused Customers
sc = pd.DataFrame({
'num_accounts': np.random.normal(2, 0.8, 3000).clip(min=1).astype(int),
'avg_annual_deposit': np.random.normal(80000, 25000, 3000).clip(min=20000),
'investment_products': np.random.normal(2, 1, 3000).clip(min=0).astype(int),
'annual_pm_income': np.random.normal(8000, 5000, 3000).clip(min=0),
'loan_amount': np.random.normal(300000, 150000, 3000).clip(min=0),
'credit_card_spending': np.random.normal(15000, 10000, 3000).clip(min=0),
'customer_tier': 'Silver'
})
# Basic Customers
bc = pd.DataFrame({
'num_accounts': np.random.normal(1, 0.5, 2000).clip(min=1).astype(int),
'avg_annual_deposit': np.random.normal(20000, 15000, 2000).clip(min=1000),
'investment_products': np.random.normal(0, 0.5, 2000).clip(min=0).astype(int),
'annual_pm_income': np.random.normal(1000, 1500, 2000).clip(min=0),
'loan_amount': np.random.normal(100000, 80000, 2000).clip(min=0),
'credit_card_spending': np.random.normal(5000, 5000, 2000).clip(min=0),
'customer_tier': 'Bronze'
})
df = pd.concat([hvnc, aic, sc, bc], ignore_index=True)
df['customer_id'] = range(1, len(df) + 1)
df = df.sample(frac=1).reset_index(drop=True)
return df
df = generate_customer_segments()
print(f"Generated customer dataset: {df.shape}")
print("\nFirst 10 rows of dataset:")
print(df.head(10))
# =============================================================================
# Step 2: Data Preprocessing and Feature Engineering
# =============================================================================
print(f"\n{'=' * 70}")
print("Data Preprocessing and Feature Engineering:")
print(f"{'=' * 70}")
print(f"\nMissing values statistics:")
print(df.isnull().sum())
# Calculate derived features
df['deposit_to_loan_ratio'] = df['avg_annual_deposit'] / (df['loan_amount'] + 1)
df['investment_activity'] = df['investment_products'] * df['annual_pm_income'] / (df['avg_annual_deposit'] + 1)
df['consumption_ability'] = df['credit_card_spending'] / (df['avg_annual_deposit'] + 1)
df['account_health_score'] = df['num_accounts'] + df['investment_products'] + np.log1p(df['annual_pm_income'])
print("\nDerived features example:")
print(df[['deposit_to_loan_ratio', 'investment_activity', 'consumption_ability', 'account_health_score']].head())
clustering_features = [
'avg_annual_deposit', 'investment_products', 'annual_pm_income',
'loan_amount', 'credit_card_spending', 'deposit_to_loan_ratio',
'investment_activity', 'consumption_ability', 'account_health_score'
]
X = df[clustering_features].copy()
print(f"\nOutlier Detection (z-score > 3):")
z_scores = np.abs(zscore(X))
outlier_mask = (z_scores > 3).any(axis=1)
n_outliers = outlier_mask.sum()
print(f"Detected {n_outliers} outliers ({n_outliers / len(df) * 100:.2f}%)")
for col in X.columns:
q1 = X[col].quantile(0.01)
q99 = X[col].quantile(0.99)
X[col] = X[col].clip(lower=q1, upper=q99)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
print(f"\nFeature scaling statistics:")
print(f"Mean (should be ~0): {X_scaled.mean(axis=0)}")
print(f"Std Dev (should be 1): {X_scaled.std(axis=0)}")
# =============================================================================
# Step 3: Determine Optimal Number of Clusters
# =============================================================================
print(f"\n{'=' * 70}")
print("Determining Optimal Number of Clusters Using Multiple Metrics:")
print(f"{'=' * 70}")
k_range = range(2, 11)
evaluation_metrics = {
'k': [],
'inertia': [],
'silhouette_score': [],
'davies_bouldin_index': [],
}
for k in k_range:
print(f"Evaluating k={k}...", end='', flush=True)
kmeans = KMeans(n_clusters=k, init='k-means++', max_iter=300,
n_init=20, random_state=42)
labels = kmeans.fit_predict(X_scaled)
evaluation_metrics['k'].append(k)
evaluation_metrics['inertia'].append(kmeans.inertia_)
evaluation_metrics['silhouette_score'].append(silhouette_score(X_scaled, labels))
evaluation_metrics['davies_bouldin_index'].append(davies_bouldin_score(X_scaled, labels))
print(f" Silhouette Score={evaluation_metrics['silhouette_score'][-1]:.4f}")
metrics_df = pd.DataFrame(evaluation_metrics)
print("\nClustering Evaluation Results Summary:")
print(metrics_df.to_string(index=False))
fig, axes = plt.subplots(1, 3, figsize=(18, 5))
fig.suptitle('Bank Customer Segmentation: Cluster Number Selection Evaluation', fontsize=16, fontweight='bold', y=1.00)
# Inertia
axes[0].plot(metrics_df['k'], metrics_df['inertia'], 'bo-', linewidth=2.5, markersize=10)
axes[0].set_xlabel('Number of Clusters (k)', fontsize=12, fontweight='bold')
axes[0].set_ylabel('Inertia', fontsize=12, fontweight='bold')
axes[0].set_title('Elbow Method: Inertia vs Cluster Number', fontsize=13, fontweight='bold')
axes[0].grid(True, alpha=0.3)
# Silhouette Score
axes[1].plot(metrics_df['k'], metrics_df['silhouette_score'], 'gs-', linewidth=2.5, markersize=10)
optimal_silhouette_idx = metrics_df['silhouette_score'].idxmax()
optimal_k_silhouette = metrics_df.loc[optimal_silhouette_idx, 'k']
axes[1].axvline(x=optimal_k_silhouette, color='r', linestyle='--',
linewidth=2.5, label=f'Optimal k={int(optimal_k_silhouette)}')
axes[1].set_xlabel('Number of Clusters (k)', fontsize=12, fontweight='bold')
axes[1].set_ylabel('Silhouette Score', fontsize=12, fontweight='bold')
axes[1].set_title('Silhouette Score Evaluation', fontsize=13, fontweight='bold')
axes[1].legend(fontsize=11, loc='best')
axes[1].grid(True, alpha=0.3)
# Davis-Bouldin Index
axes[2].plot(metrics_df['k'], metrics_df['davies_bouldin_index'], 'rs-', linewidth=2.5, markersize=10)
optimal_db_idx = metrics_df['davies_bouldin_index'].idxmin()
optimal_k_db = metrics_df.loc[optimal_db_idx, 'k']
axes[2].axvline(x=optimal_k_db, color='r', linestyle='--',
linewidth=2.5, label=f'Optimal k={int(optimal_k_db)}')
axes[2].set_xlabel('Number of Clusters (k)', fontsize=12, fontweight='bold')
axes[2].set_ylabel('Davies-Bouldin Index', fontsize=12, fontweight='bold')
axes[2].set_title('DB Index Evaluation', fontsize=13, fontweight='bold')
axes[2].legend(fontsize=11, loc='best')
axes[2].grid(True, alpha=0.3)
plt.tight_layout()
plt.savefig('cluster_number_evaluation.png', dpi=300, bbox_inches='tight')
plt.show()
optimal_k = int(optimal_k_silhouette)
print(f"\nOptimal number of clusters based on silhouette score: k = {optimal_k}")
# =============================================================================
# Step 4: Final Clustering with Optimal k
# =============================================================================
print(f"\n{'=' * 70}")
print(f"Performing Final Clustering (k={optimal_k}):")
print(f"{'=' * 70}")
kmeans_final = KMeans(n_clusters=optimal_k, init='k-means++',
max_iter=500, n_init=30, random_state=42)
df['cluster_id'] = kmeans_final.fit_predict(X_scaled)
print(f"Final Silhouette Score: {silhouette_score(X_scaled, df['cluster_id']):.4f}")
print(f"Actual Iterations: {kmeans_final.n_iter_}")
# =============================================================================
# Step 5: In-Depth Analysis of Each Customer Segment
# =============================================================================
print(f"\n{'=' * 70}")
print("Detailed Analysis of Each Customer Segment:")
print(f"{'=' * 70}")
cluster_analysis = {}
for cluster_id in range(optimal_k):
cluster_data = df[df['cluster_id'] == cluster_id]
size = len(cluster_data)
percentage = size / len(df) * 100
print(f"\n【Customer Segment {cluster_id}】")
print(f"{'---' * 60}")
print(f"Segment Size: {size} customers ({percentage:.2f}%)")
print(f"Total Customer Value: RMB {cluster_data['avg_annual_deposit'].sum():,.0f}")
for feature in ['avg_annual_deposit', 'investment_products', 'annual_pm_income',
'loan_amount', 'credit_card_spending']:
avg = cluster_data[feature].mean()
std = cluster_data[feature].std()
print(f"{feature}:")
print(f" Mean: {avg:,.0f}, Std Dev: {std:,.0f}, Median: {cluster_data[feature].median():,.0f}")
avg_deposit = cluster_data['avg_annual_deposit'].mean()
avg_investment = cluster_data['investment_products'].mean()
avg_loan = cluster_data['loan_amount'].mean()
if avg_deposit > 300000 and avg_investment > 6:
group_type = 'High Net Worth Customers (Priority Service Target)'
elif avg_deposit > 100000 and avg_investment > 4:
group_type = 'Active Investment Customers (Key Development Target)'
elif avg_deposit > 30000:
group_type = 'Stable Savings Customers (Retention Target)'
else:
group_type = 'Basic Customers (Development Target)'
print(f"Segment Label: {group_type}")
cluster_analysis[cluster_id] = {
'size': size,
'percentage': percentage,
'type': group_type,
'data': cluster_data
}
# =============================================================================
# Step 6: Visualize Clustering Results (PCA Dimensionality Reduction to 2D)
# =============================================================================
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)
print(f"\n{'=' * 70}")
print("PCA Dimensionality Reduction Information:")
print(f"{'=' * 70}")
print(f"PC1 Variance Explained Ratio: {pca.explained_variance_ratio_[0]:.4f}")
print(f"PC2 Variance Explained Ratio: {pca.explained_variance_ratio_[1]:.4f}")
print(f"Cumulative Variance Explained: {pca.explained_variance_ratio_.sum():.4f}")
fig, axes = plt.subplots(1, 2, figsize=(18, 7))
fig.suptitle('Bank Customer Clustering Analysis Results', fontsize=16, fontweight='bold')
# Clustering results visualization
scatter = axes[0].scatter(X_pca[:, 0], X_pca[:, 1], c=df['cluster_id'],
cmap='viridis', alpha=0.6, s=60, edgecolors='black', linewidth=0.5)
centers_pca = pca.transform(kmeans_final.cluster_centers_)
axes[0].scatter(centers_pca[:, 0], centers_pca[:, 1],
c='red', marker='X', s=800, edgecolors='black', linewidth=2.5,
label='Cluster Centers', zorder=5)
axes[0].set_xlabel(f'PC1 ({pca.explained_variance_ratio_[0]:.1%})',
fontsize=12, fontweight='bold')
axes[0].set_ylabel(f'PC2 ({pca.explained_variance_ratio_[1]:.1%})',
fontsize=12, fontweight='bold')
axes[0].set_title('Customer Segments PCA Visualization', fontsize=13, fontweight='bold')
axes[0].legend(fontsize=11)
axes[0].grid(True, alpha=0.3)
cbar = plt.colorbar(scatter, ax=axes[0], label='Customer Segment')
# Segment size and value distribution
cluster_sizes = df['cluster_id'].value_counts().sort_index()
cluster_values = df.groupby('cluster_id')['avg_annual_deposit'].sum().sort_index()
x = np.arange(optimal_k)
width = 0.35
ax2 = axes[1]
bars1 = ax2.bar(x - width / 2, cluster_sizes, width, label='Number of Customers',
alpha=0.8, color='skyblue', edgecolor='black', linewidth=1.5)
ax2_2 = ax2.twinx()
bars2 = ax2_2.bar(x + width / 2, cluster_values / 1000000, width, label='Total Deposits (Million RMB)',
alpha=0.8, color='coral', edgecolor='black', linewidth=1.5)
for i, (bar, val) in enumerate(zip(bars1, cluster_sizes)):
ax2.text(bar.get_x() + bar.get_width() / 2, val, f'{int(val)}',
ha='center', va='bottom', fontsize=10, fontweight='bold')
for i, (bar, val) in enumerate(zip(bars2, cluster_values / 1000000)):
ax2_2.text(bar.get_x() + bar.get_width() / 2, val, f'{val:.1f}',
ha='center', va='bottom', fontsize=10, fontweight='bold')
ax2.set_xlabel('Customer Segment', fontsize=12, fontweight='bold')
ax2.set_ylabel('Number of Customers', fontsize=12, fontweight='bold', color='skyblue')
ax2_2.set_ylabel('Total Deposits (Million RMB)', fontsize=12, fontweight='bold', color='coral')
ax2.set_title('Segment Size and Value Distribution', fontsize=13, fontweight='bold')
ax2.set_xticks(x)
ax2.set_xticklabels([f'Segment {i}' for i in range(optimal_k)], fontsize=11, fontweight='bold')
ax2.tick_params(axis='y', labelcolor='skyblue')
ax2_2.tick_params(axis='y', labelcolor='coral')
lines1, labels1 = ax2.get_legend_handles_labels()
lines2, labels2 = ax2_2.get_legend_handles_labels()
ax2.legend(lines1 + lines2, labels1 + labels2, loc='upper left', fontsize=11)
ax2.grid(True, alpha=0.3, axis='y')
plt.tight_layout()
plt.savefig('clustering_results_visualization.png', dpi=300, bbox_inches='tight')
plt.show()
# =============================================================================
# Step 7: Generate Actionable Marketing Strategy Recommendations
# =============================================================================
print(f"\n{'=' * 70}")
print("Marketing Strategy Recommendations Based on Clustering Results:")
print(f"{'=' * 70}")
strategies = {
0: {
'objective': 'Maintenance and Upgrade',
'actions': [
'Provide dedicated VIP account manager service',
'Host exclusive premium wealth management seminars',
'Recommend high-end investment products and custom services',
'Offer priority loan approval and preferential interest rates',
'Invite participation in important bank activities and decisions',
]
},
1: {
'objective': 'Key Development',
'actions': [
'Strengthen promotion of investment products',
'Provide customized asset allocation plans',
'Recommend diversified investment products',
'Establish regular communication with investment advisors',
'Consider upgrade path to VIP customer tier',
]
},
2: {
'objective': 'Stability and Incentive',
'actions': [
'Offer competitive fixed deposit interest rates',
'Promote safe and stable investment products',
'Regular promotional offers for deposit appreciation',
'Invite participation in inclusive finance products',
'Encourage upgrade to investment customer tier',
]
},
3: {
'objective': 'Development and Cultivation',
'actions': [
'Provide basic financial education and consultation',
'Recommend products aligned with risk preference',
'Establish regular communication mechanism',
'Offer small loans and credit card products',
'Gradually cultivate into higher-value customers',
]
}
}
for cluster_id in range(min(optimal_k, 4)):
if cluster_id in strategies:
strategy = strategies[cluster_id]
cluster_data = df[df['cluster_id'] == cluster_id]
print(f"\n【Segment {cluster_id}】- {strategy['objective']}")
print(f"Size: {len(cluster_data)} customers, Total Value: RMB {cluster_data['avg_annual_deposit'].sum():,.0f}")
for i, action in enumerate(strategy['actions'], 1):
print(f" {i}. {action}")
# =============================================================================
# Step 8: Export Results
# =============================================================================
result_export = df[['customer_id', 'avg_annual_deposit', 'investment_products',
'annual_pm_income', 'credit_card_spending', 'cluster_id']].copy()
result_export.columns = ['customer_id', 'annual_deposit_rmb', 'investment_products_count',
'annual_pm_income_rmb', 'annual_card_spending_rmb', 'recommended_segment']
result_export.to_csv('bank_customer_segmentation_results.csv', index=False)
print(f"\n✓ Clustering results exported to 'bank_customer_segmentation_results.csv'")
model_info = {
'num_clusters': optimal_k,
'silhouette_score': silhouette_score(X_scaled, df['cluster_id']),
'num_features': len(clustering_features),
'num_samples': len(df),
'features_used': ', '.join(clustering_features)
}
print(f"\n{'=' * 70}")
print("Clustering Model Information Summary:")
print(f"{'=' * 70}")
for key, value in model_info.items():
print(f"{key}: {value}")
print(f"\n✓ Analysis complete! All charts have been saved to the current directory.")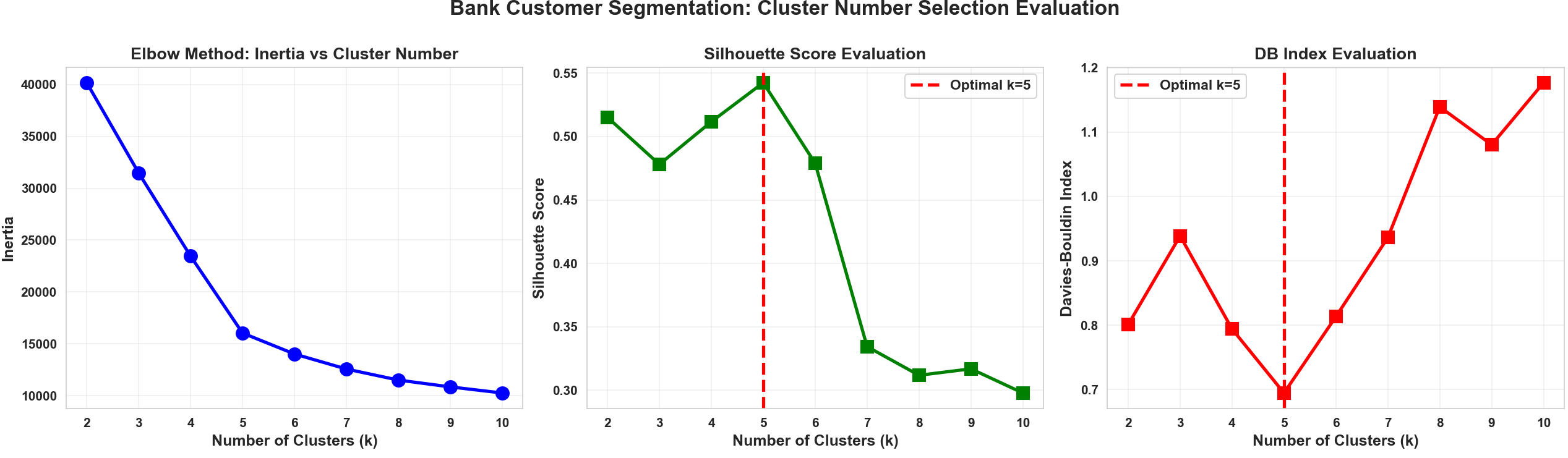
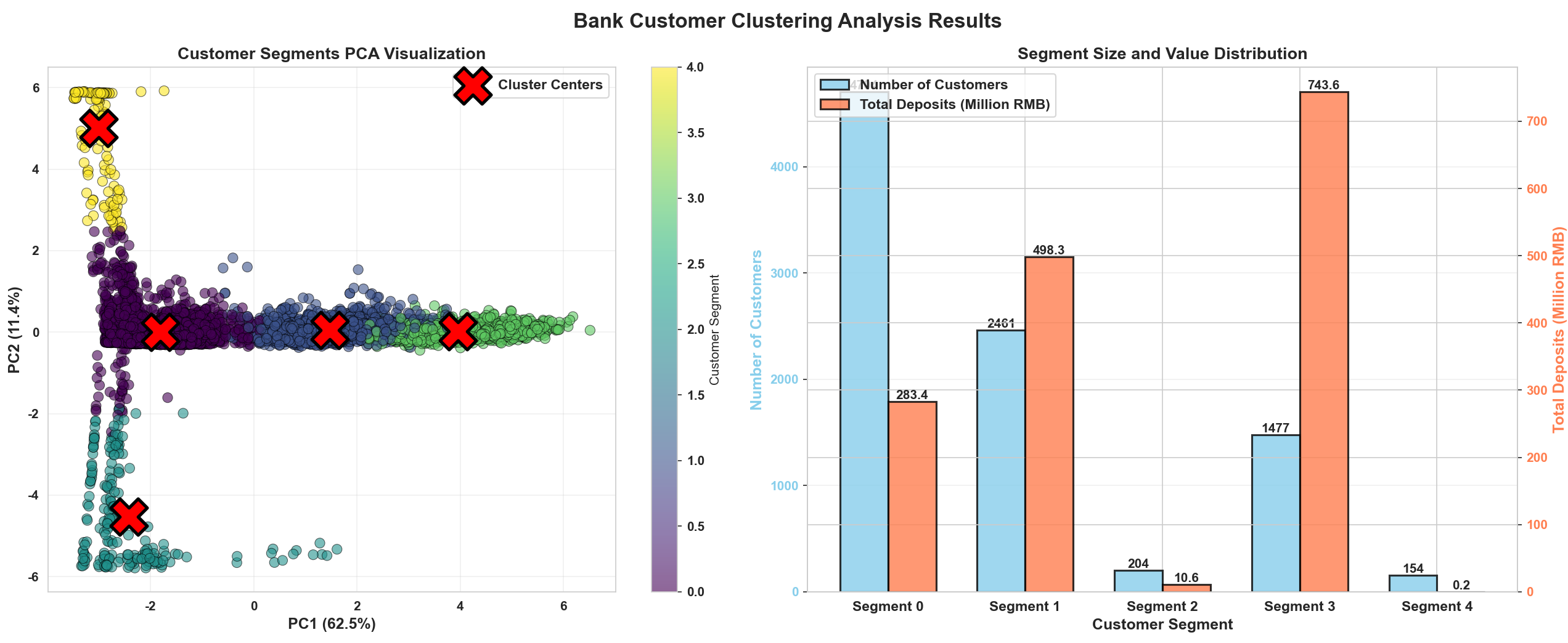
这个完整的银行客户分群案例展示了K-Means在真实商业场景中的应用全过程,包括数据准备、特征工程、聚类分析、结果解释和业务应用。
第9章 K-Means的性能优化与工程实现
9.1 计算性能优化技巧
在处理大规模数据集时,K-Means的计算性能至关重要。除了使用Mini-Batch K-Means外,还有多个优化策略可以加速计算。首先,距离计算的优化是关键。标准的K-Means计算欧氏距离,可以利用数学恒等式来加速计算,避免重复计算平方项。许多库已经实现了这种优化。
其次,可以使用GPU加速。对于具有足够规模的数据集(通常>1百万样本),使用GPU库如RAPIDS cuML可以将K-Means的计算时间从几分钟降低到几秒。GPU特别擅长矩阵运算,而K-Means主要涉及大量的矩阵计算。
第三,可以使用稀疏矩阵表示。当数据是高维但稀疏的(如文本向量),使用稀疏矩阵可以显著节省内存和计算时间。Scikit-learn的KMeans支持稀疏输入。
第四,可以在多个CPU核心上并行化。Scikit-learn的KMeans在n_jobs参数支持下可以利用多核并行计算。对于拥有多核处理器的现代计算机,这可以带来显著的性能提升。
9.2 生产环境中的K-Means部署
在生产环境中部署K-Means模型需要考虑多个方面。首先,模型持久化和加载。通常使用pickle或joblib来序列化和保存训练好的KMeans模型,以便后续使用。
其次,在线学习和增量更新。当新数据不断到来时,完整重新训练K-Means可能不现实。Mini-Batch KMeans支持partial_fit方法,可以用新数据增量更新模型。
第三,模型监控和性能追踪。需要定期评估生产模型的性能,监控聚类结果的稳定性和质量,检测数据分布是否发生了显著变化(数据漂移),如果发生则触发模型重训。
第四,版本控制和实验追踪。使用MLflow等工具来追踪不同版本的模型,记录训练参数、评估指标等,便于模型的可重现性和比较。
第10章 结论与未来发展方向
K-Means聚类算法虽然在1950年代就被提出,但时至今日仍然是最常用、最实用的聚类算法之一。其简洁的原理、高效的计算、易用的实现和出色的实际效果使其在学术和工业界都得到了广泛应用。通过本文详尽的理论阐述、丰富的代码实现和真实的应用案例,我们可以看到K-Means在数据科学和机器学习中的重要地位。
K-Means能够帮助我们从无标记的原始数据中发现隐含的结构,实现数据的智能分组。无论是电商的客户分群、图像处理的颜色量化、还是金融的风险分类,K-Means都展现了其强大而灵活的适应性。同时,通过与其他算法的结合(如PCA、深度学习等)和多种扩展(如Mini-Batch、核K-Means等),K-Means的应用范围不断扩大。
未来,K-Means的发展方向主要包括以下几个方面:(1)更好的可扩展性,尤其是在流式数据和极端规模数据上的应用;(2)与深度学习的更深层次融合,如端到端的深度聚类网络;(3)处理更复杂的数据类型,如图数据、序列数据、多模态数据等;(4)更好的理论分析,包括收敛速率分析、近似比分析等;(5)更强的鲁棒性,特别是对离群值、噪声和数据质量问题的处理。
总的来说,K-Means是一个经典而强大的算法,值得每一个从事数据科学工作的人深入学习和掌握。通过本文的学习,希望读者能够不仅理解K-Means的原理,更重要的是能够在实际工作中灵活运用它来解决真实的问题,发现数据中的价值和洞见。