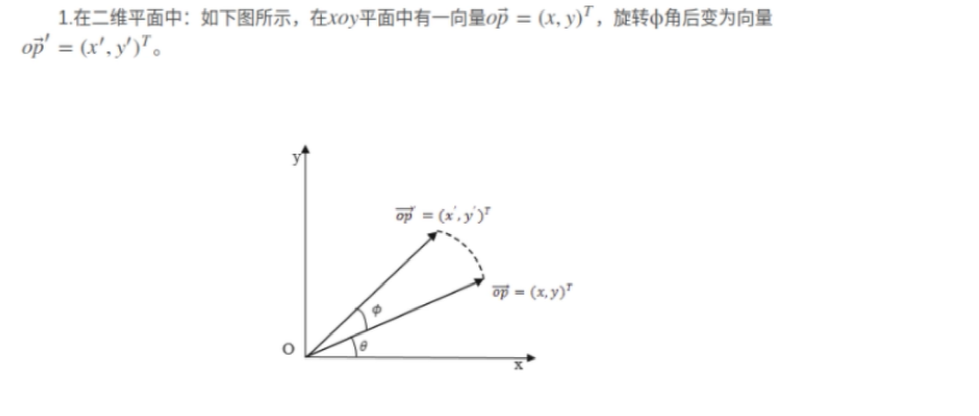
1.Transformer 的正弦位置编码:

import torch
from torch import nn
class PositionalEncoding(nn.Module):
def __init__(self, d_model, max_len=5000, dropout=0.1):
super(PositionalEncoding, self).__init__()
self.dropout = nn.Dropout(p=dropout)
# 创建位置编码表 pe,形状为 [max_len, d_model]
pe = torch.zeros(max_len, d_model)
# 位置索引 [0, 1, ..., max_len-1],形状为 [max_len, 1]
position = torch.arange(0, max_len).unsqueeze(1) # [max_len, 1]
# 计算每个维度的除数项:10000^(2i/d_model),其中 i 为偶数维度索引
div_term = 10000 ** (torch.arange(0, d_model, 2).float() / d_model) # [d_model//2]
# 偶数维度使用 sin,奇数维度使用 cos
pe[:, 0::2] = torch.sin(position / div_term) # 偶数维度:sin(pos / 10000^(2i/d))
pe[:, 1::2] = torch.cos(position / div_term) # 奇数维度:cos(pos / 10000^(2i/d))
# 转换为 [1, max_len, d_model],方便广播到 batch 和 seq_len
pe = pe.unsqueeze(0) # [1, max_len, d_model]
# 注册为缓冲区(不参与训练)
self.register_buffer('pe', pe)
def forward(self, x):
"""
输入: x: [batch_size, seq_len, d_model]
输出: 加上对应位置编码后的输出
"""
# 取前 x.size(1) 个位置编码(避免越界)
x = x + self.pe[:, :x.size(1), :] # 广播加法
return self.dropout(x)
if __name__ == '__main__':
# 示例:构建一个位置编码器
pos_enc = PositionalEncoding(d_model=512, max_len=100)
# 假设输入是 [batch_size=2, seq_len=10, d_model=512]
x = torch.randn(2, 10, 512)
# 前向传播
output = pos_enc(x)
print(output.shape) # torch.Size([2, 10, 512])关键点解析
| 步骤 | 说明 |
|---|---|
pe = torch.zeros(max_len, d_model) |
初始化位置编码矩阵 |
position = torch.arange(...).unsqueeze(1) |
构造位置索引列向量 |
div_term = 10000 ** (torch.arange(0, d_model, 2) / d_model) |
每个偶数维度对应的频率缩放因子 |
pe[:, 0::2] = sin(...) |
偶数维用正弦函数 |
pe[:, 1::2] = cos(...) |
奇数维用余弦函数 |
pe.unsqueeze(0) |
扩展维度为 [1, max_len, d_model],便于广播 |
self.register_buffer('pe', pe) |
将 pe 注册为缓冲区,不参与梯度更新 |
x + self.pe[:, :x.size(1), :] |
只取需要的位置编码长度,避免越界 |
输出结果
torch.Size([2, 10, 512])表示:对输入序列加上了对应位置编码,并保留原始 shape。
2.相对位置编码ROPE
正弦位置编码的"外推性"在理论上成立,但在实践中存在严重缺陷,尤其在长序列任务中表现不佳。而RoPE 等相对位置编码方法通过更符合语言本质的设计,显著提升了模型对长距离依赖的建模能力、外推稳定性和训练效率。





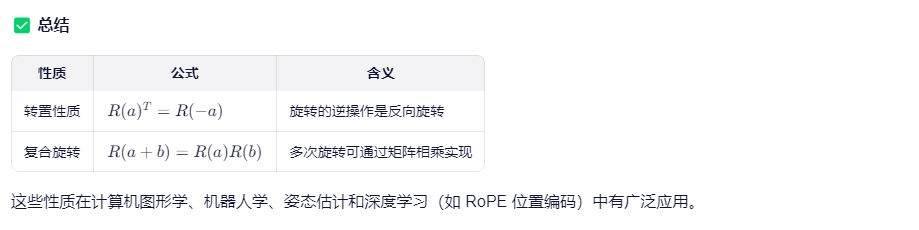

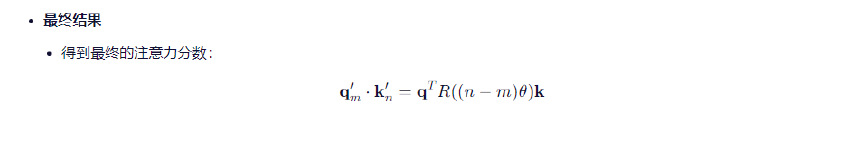
结论:
注意力分数只依赖于相对位置差(n-m),与绝对位置m、n无关!
RoPE 通过旋转 query 和 key 向量来编码位置信息,利用旋转矩阵的代数性质,使得注意力分数只依赖于相对位置 (n−m),从而实现了高效、稳定的相对位置建模。
- 注意力分数只与相对位置 m−n 有关
- 不依赖绝对位置,而是关注"相隔多远"。
- 模型天然知道两个词相隔多远,无需额外学习
- 相对关系被直接编码进内积中。
- 外推时,只要相对距离在合理范围内,注意力机制依然有效
- 即使序列更长,只要 ∣m−n∣ 在训练范围以内,模型仍能正确建模。
RoPE 的实现方式:将 query 和 key 分别进行旋转,使得它们的内积只依赖于相对偏移。
类比:就像你不需要知道两个人的具体出生年份,只要知道"他比我大5岁",就能理解他们的年龄关系。
关键优势:RoPE 让注意力机制显式地感知相对位置,而不是隐式地从绝对位置中学习。
RoPE 如何解决正弦 PE 的根本缺陷?
| 正弦 PE 的问题 | RoPE 的解决方案 |
|---|---|
| 绝对位置编码,不符合语言直觉 | → 使用相对位置,符合人类对"前后关系"的认知 |
| 高频震荡导致局部信息丢失 | → 旋转操作保持向量内积的平滑性,避免剧烈波动 |
| 模型需从绝对位置推导相对关系 | → 相对关系直接编码在注意力计算中,无需推理 |
| 外推时信号失真 | → 通过 NTK-aware 插值等技术可安全扩展上下文长度 |
为什么需要 RoPE?------ 总结观点
| 观点 | 解释 |
|---|---|
| "有外推性" ≠ "好外推性" | 正弦 PE 能算出值,但信号质量差,模型学不到有效模式;RoPE 外推稳定且有意义 |
| 语言是相对的 | 人类靠"前后关系"理解句子,不是靠"第几个字";RoPE 更贴近语言本质 |
| RoPE 更高效、更稳定 | 直接建模相对位置,减少模型学习负担,提升长程依赖建模能力 |
| 现代大模型的选择 | LLaMA、ChatGLM、Falcon 等主流大模型全部采用 RoPE 或其变种 |
最终结论:
正弦位置编码是一个优雅的理论起点,但 RoPE 是工程实践的进化。
-
它解决了传统位置编码在长序列建模、外推能力、语言相对性建模上的核心瓶颈。
-
成为现代 Transformer 模型(尤其是大模型)的标准配置。
import torch
import torch.nn as nnclass RotaryPositionEncodingStandard(nn.Module):
def init(self, d_model, max_len=5000, dropout=0.1):
super(RotaryPositionEncodingStandard, self).init()
inv_freq = 1 / (10000 ** (torch.arange(0, d_model, 2).float() / d_model))
self.register_buffer('inv_freq', inv_freq)
self._build_cache(max_len)def _build_cache(self, seq_len): """ 预计算 cos 和 sin 缓存,避免每次 forward 重复计算 """ positions = torch.arange(seq_len, device=self.inv_freq.device).float().unsqueeze(1) # [seq_len, 1] freqs = positions * self.inv_freq # [seq_len, d_model//2] # 将 freqs 在最后一个维度重复两次(对应偶数/奇数维度) emb = torch.repeat_interleave(freqs, 2, dim=-1) # [seq_len, d_model] # 注册为 buffer,不参与训练 self.register_buffer('cos_cached', emb.cos(), persistent=False) self.register_buffer('sin_cached', emb.sin(), persistent=False) # ⚠️ persistent=False 表示该 buffer 不会被保存到 state_dict 中 # 适用于可重新计算的缓存(如 RoPE 的 cos/sin 只依赖 max_seq_len 和 head_dim) # 减少 checkpoint 文件大小;加载时若缺失可在 __init__ 或 forward 中重建 def rotate_half(self, x): """ 对向量进行"旋转一半"操作: 将偶数维度和奇数维度交换,并对奇数维度取负号 即:[x0, x1, x2, x3] → [-x1, x0, -x3, x2] """ x_even = x[..., 0::2] # 偶数索引 x_odd = x[..., 1::2] # 奇数索引 # 分割前半和后半(按维度切分) x_even = x_even[..., :x.shape[-1] // 2] # 前半 x_odd = x_odd[..., x.shape[-1] // 2:] # 后半 # 构造旋转后的向量:[-x_odd, x_even] rotated = torch.stack([-x_odd, x_even], dim=-1) return rotated.reshape(x.shape) def forward(self, x, seq_dim=1): """ 输入: x: [batch_size, seq_len, d_model] 输出: 经过 RoPE 编码后的向量 """ seq_len = x.size(seq_dim) if seq_len > self.cos_cached.size(0): self._build_cache(seq_len) # 动态扩展缓存 cos = self.cos_cached[:seq_len] # [seq_len, d_model] sin = self.sin_cached[:seq_len] # [seq_len, d_model] # 扩展 batch 维度以匹配输入形状 cos = cos.unsqueeze(0) # [1, seq_len, d_model] sin = sin.unsqueeze(0) # [1, seq_len, d_model] # RoPE 公式:x' = x * cos + rotate_half(x) * sin return x * cos + self.rotate_half(x) * sinif name == 'main':
# 示例:构建一个 RoPE 编码器
x = torch.rand(2, 10, 512) # (batch=2, seq_len=10, dim=512)
print(f"输入形状: {x.shape}")rope = RotaryPositionEncodingStandard(d_model=512) result = rope(x) print(f"输出形状: {result.shape}") # print(f"输出:\n{result}")