数据结构——二叉树

二叉树

• 一、二叉树
• • 1.1、二叉树的类型
  • 1.2、二叉树的性质
  • 1.3、二叉树的结构
  • 1.4、二叉树的操作
  • 1.5、二叉树的应用
• 二、二叉树的遍历
• • 2.1、遍历的方式
  • 2.2、遍历的分类
  • 2.3、前序遍历
  • 2.4、非递归前序遍历
  • 2.5、中序遍历
  • 2.6、非递归中序遍历
  • 2.7、后序遍历
  • 2.8、非递归后续遍历
  • 2.9、层次遍历
• 三、二叉树相关问题
• • 3.1、查找二叉树中最大元素
  • 3.2、非递归查找二叉树中最大值
  • 3.3、在二叉树中搜索某个元素
  • 3.4、非递归在二叉树中搜索某个元素
  • 3.5、实现将一个元素插入二叉树中的算法
  • 3.6、获取二叉树节点个数
  • 3.7、非递归获取二叉树节点个数
  • 3.8、实现删除数树的算法
  • 3.9、逆向逐层输出元素
  • 3.10、求二叉树高度
  • 3.11、非递归求二叉树高度
  • 3.12、查找二叉树中最深节点
  • 3.13、非递归获取二叉树中叶子节点个数
  • 3.14、非递归查找二叉树中满节点个数
  • 3.15、非递归查找二叉树中的半节点
  • 3.16、判断两颗二叉树结构是否相同
  • 3.17、求二叉树直径
  • 3.18、求二叉树同一层节点数据之和最大的层
  • 3.19、输出所有从根节点到叶子节点的路径
  • 3.20、判断是否存在路径的数据和等于给定值
  • 3.21、二叉树镜像转换
  • 3.21、判断两颗二叉树是否互为镜像
  • 3.22、根据中序和前序遍历构建二叉树
  • 3.23、查找二叉树中两个节点的最近公共祖先

一、二叉树

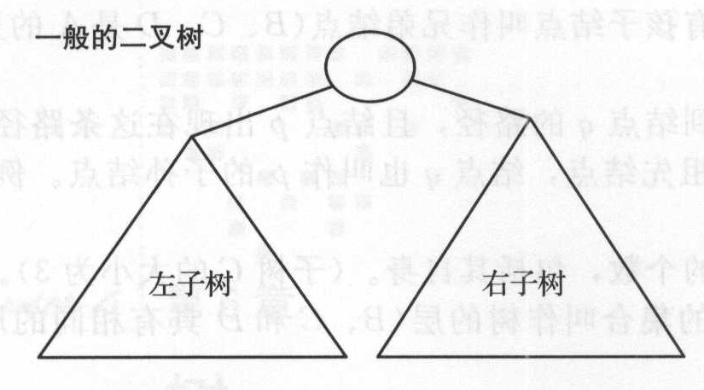
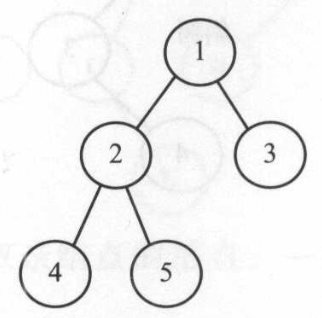
如果一棵树中的每个结点有0、1或者2个孩子结点，那么这棵树就称为二叉树。空树也是一棵有效的二叉树。一棵二叉树可以看作由根结点和两棵不相交的子树（分别称为左子树和右子树)组成。如下图所示。

1.1、二叉树的类型

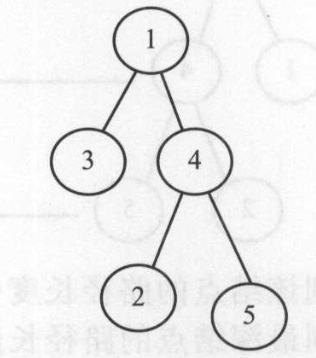
严格二叉树：二叉树中的每个节点要么有两个孩子节点，要么没有孩子节点。

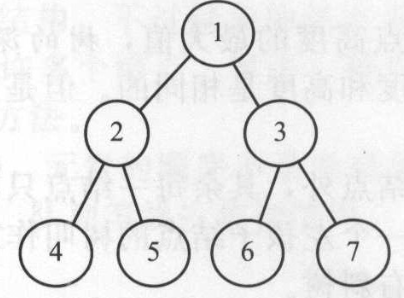
满二叉树 ：二叉树中的每个节点恰好有两个孩子节点且所有叶子节点都在同一层。

完全二叉树：在定义完全二叉树之前，假定二叉树的高度为h。对于完全二叉树，如果将所有结点从根结点开始从左至右，从上至下，依次编号（假定根结点的编号为1），那么将得到从1~n(n为结点总数)的完整序列。在遍历过程中对于空指针也应赋予编号。如果所有叶子结点的深度为h或h一1，且在结点编号序列中没有漏掉任何数字，那么这样的二叉树叫作完全二叉树。

1.2、二叉树的性质

假定数的高度为h，且根节点的深度为0。

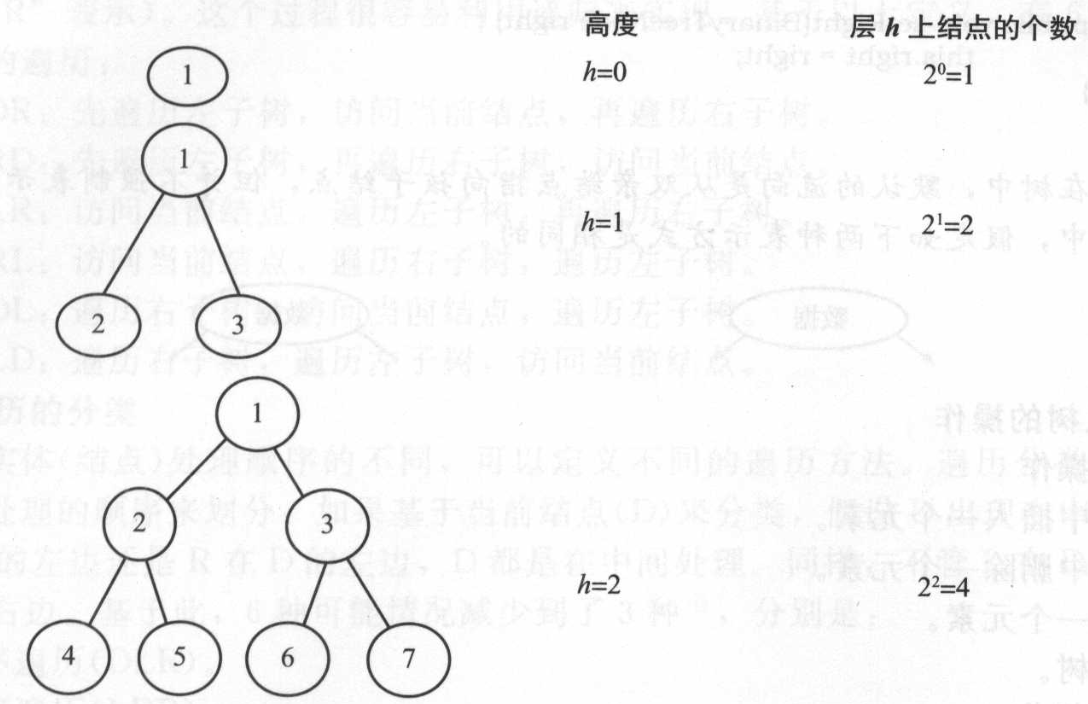
• 满二叉树的结点个数n为2^h+1-1。因为该树共有h层，所以每一层的结点个数都是满的。
• 完全二叉树的结点个数为2^h~2^h+1-1。
• 满二叉树的叶子结点个数是2^h。
• 对于n个结点的完全二叉树，空指针的个数为n十1。

1.3、二叉树的结构

接下来定义二叉树的结构。为了简单起见，假定结点的数据为整数。表示一个结点(包含数据)的方法之一是定义两个指针，一个指向左孩子结点，另一个指向右孩子结点，中间为数据字段（如下图所示）。

public class BinaryTreeNode {
    private int data;               //数据
    private BinaryTreeNode left;    //左孩子引用
    private BinaryTreeNode right;   //右孩子引用

    public BinaryTreeNode(int data) {
        this.data = data;
    }

    public int getData() {
        return data;
    }

    public void setData(int data) {
        this.data = data;
    }

    public BinaryTreeNode getLeft() {
        return left;
    }

    public void setLeft(BinaryTreeNode left) {
        this.left = left;
    }

    public BinaryTreeNode getRight() {
        return right;
    }

    public void setRight(BinaryTreeNode right) {
        this.right = right;
    }
}

1.4、二叉树的操作

• 基本操作 ：
  • 向树中插入一个元素。
  • 从树中删除一个元素。
  • 查找一个元素。
  • 遍历树。
• 辅助操作 ：
  • 获取树的大小。
  • 获取树的高度。
  • 获取其和最大的层。
  • 对于给定的两个或多个节点，找出它们的最近公共祖先（Least Common Ancestor, LCA）

1.5、二叉树的应用

• 编译器中的表达式树。
• 用于数据压缩算法中的赫夫曼编码树。
• 支持在集合中查找、插入和删除，其平均时间复杂度为O(1og)的二叉搜索（或称为查找)树(BST)。
• 优先队列(PQ)，它支持以对数时间（最坏情况下）对集合中的最小（或最大）数据元素进行搜索和删除。

二、二叉树的遍历

2.1、遍历的方式

从二叉树的根结点开始遍历，需要执行3个主要步骤。这3个步骤执行的不同顺序定义了树的不同遍历类型。这3个步骤是：在当前结点上执行一个动作（对应于访问当前结点，用符号"D"表示)；遍历该结点的左子树（用符号"L"表示）；遍历该结点的右子树(用符号"R"表示)。这个过程很容易利用递归来实现。基于以上定义，有6种可能方法来实现树的遍历：

1. LDR:先遍历左子树，访问当前结点，再遍历右子树。
2. LRD:先遍历左子树，再遍历右子树，访问当前结点。
3. DLR:访问当前结点，遍历左子树，再遍历右子树。
4. DRL:访问当前结点，遍历右子树，遍历左子树。
5. RDL:遍历右子树，访问当前结点，遍历左子树。
6. RLD:遍历右子树，遍历左子树，访问当前结点。

2.2、遍历的分类

根据实体（结点）处理顺序的不同，可以定义不同的遍历方法。遍历分类可以根据当前结点被处理的顺序来划分：如果基于当前结点(D)来分类，假设D出现在中间，那么不管L在D的左边还是R在D的左边，D都是在中间处理。同样，不管L在D的右边还是R在D的右边。基于此，6种可能情况减少到了3种，分别是：

• 前序遍历(DLR)。
• 中序遍历(LDR)。
• 后序遍历(LRD)。
• 层次遍历：这种方法从图的广度优先遍历方法启发得来。

2.3、前序遍历

在前序遍历中，每个结点都是在它的子树遍历之前进行处理。这是最容易理解的遍历方法。然而，尽管每个结点在其子树之前进行了处理，但在向下移动的过程中仍然需要保留一些信息。以上图为例，首先访问结点1，随后遍历其左子树，最后遍历其右子树。因此，当左子树遍历完后，必须要返回到其右子树来继续遍历。为了能够在左子树遍历完成后移动到右子树，必须保留根结点的信息。能够实现该信息存储的抽象数据类型显而易见是栈。由于它是LIFO结构，所以它可以以逆序来获取该信息并返回到右子树。

前序遍历可以如下定义：

• 访问根结点。
• 按前序遍历方式遍历左子树。
• 按前序遍历方式遍历右子树

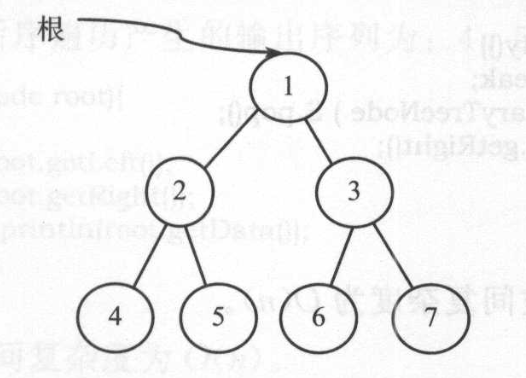
利用前序遍历方法遍历上图所示的树的输出序列为：1 2 4 5 3 6 7。时间负责度为O(n)，空间复杂度为O(n)。

/**
 * 前序遍历
 * @param root
 */
public void preOrder(BinaryTreeNode root) {
    if (root != null) {
        System.out.println(root.getData());//访问根节点
        preOrder(root.getLeft());//递归左子树
        preOrder(root.getRight());//递归右子树
    }
}

//测试
public class BinaryTreeTest {

    private BinaryTreeNode root;

    /**
     * 初始化二叉树
     *        1
     *    2      3
     *  4  5    6  7
     */
    @Before
    public void init() {
        root = new BinaryTreeNode(1);
        BinaryTreeNode root_left = new BinaryTreeNode(2);
        BinaryTreeNode root_right = new BinaryTreeNode(3);
        BinaryTreeNode root_left_left = new BinaryTreeNode(4);
        BinaryTreeNode root_left_right = new BinaryTreeNode(5);
        BinaryTreeNode root_right_left = new BinaryTreeNode(6);
        BinaryTreeNode root_right_right = new BinaryTreeNode(7);
        root.setLeft(root_left);
        root.setRight(root_right);
        root_left.setLeft(root_left_left);
        root_left.setRight(root_left_right);
        root_right.setLeft(root_right_left);
        root_right.setRight(root_right_right);
    }

    @Test
    public void testPreOrder() {
        BinaryTree binaryTree = new BinaryTree();
        binaryTree.preOrder(root);// 1 2 4 5 3 6 7
    }
}

2.4、非递归前序遍历

在递归方法中，需要采用一个栈来记录当前结点以便在完成左子树后能返回到右子树进行遍历。为了模拟相同的操作，首先处理当前结点，在遍历左子树之前，把当前结点保留到栈中，当遍历完左子树后，将该元素出栈，然后找到其右子树进行遍历。持续该过程直到栈为空。

时间负责度为O(n)，空间复杂度为O(n)。

/**
 * 非递归前序遍历
  * @param root
 */
public void preOrderNonRecursive(BinaryTreeNode root) {
    if (root == null) {
        return;
    }
    Stack<BinaryTreeNode> stack = new Stack<BinaryTreeNode>();
    while (true) {
        while (root != null) {
            System.out.println(root.getData());
            stack.push(root);
            root = root.getLeft();
        }
        if (stack.isEmpty()) {
            break;
        }
        root = stack.pop();
        root = root.getRight();
    }
    return;
}

2.5、中序遍历

在中序遍历中，根结点的访问在两棵子树的遍历中间完成。中序遍历如下定义：

• 按中序遍历方式遍历左子树。
• 访问根结点。
• 按中序遍历方式遍历右子树。

基于中序遍历，上图所示树的中序遍历输出顺序为：4 2 5 1 6 3 7。

时间负责度为O(n)，空间复杂度为O(n)。

/**
 * 中序遍历
  * @param root
 */
public void inOrder(BinaryTreeNode root) {
    if (root != null) {
        inOrder(root.getLeft());
        System.out.println(root.getData());
        inOrder(root.getRight());
    }
}

2.6、非递归中序遍历

非递归中序遍历类似于前序遍历。唯一的区别是，首先要移动到结点的左子树，完成左子树的遍历后，再将结点出栈进行处理（即发生在左子树遍历完后）。

时间负责度为O(n)，空间复杂度为O(n)。

/**
 * 非递归中序遍历
 * @param root
 */
public void inOrderNonRecursive(BinaryTreeNode root) {
    if (root == null) {
        return;
    }
    Stack<BinaryTreeNode> stack = new Stack<BinaryTreeNode>();
    while (true) {
        while (root != null) {
            stack.push(root);
            root = root.getLeft();
        }
        if (stack.isEmpty()) {
            break;
        }
        root = stack.pop();
        System.out.println(root.getData());
        root = root.getRight();
    }
    return;
}

2.7、后序遍历

在后序遍历中，根结点的访问是在其两棵子树都遍历完后进行的。后序遍历如下定义：

• 按后序遍历左子树。
• 按后序遍历右子树。
• 访问根结点。

对上图所示的二叉树，后序遍历产生的输出序列为：4 5 2 6 7 3 1。

时间负责度为O(n)，空间复杂度为O(n)。

/**
 * 后序遍历
 * @param root
 */
public void postOrder(BinaryTreeNode root) {
    if (root != null) {
        postOrder(root.getLeft());
        postOrder(root.getRight());
        System.out.println(root.getData());
    }
}

2.8、非递归后续遍历

在前序和中序遍历中，当元素出栈后就不需要再次访问该结点了。但是在后序遍历中，每个结点需要访问两次。这就意味着，在遍历完左子树后，需要访问当前结点，之后遍历完右子树时还需要访问该当前结点。但只有在第二次访问时才处理当前结点。问题是如何区分这两次访问：到底是遍历完左子树后的返回还是遍历完右子树后的返回？

解决这个问题的方法是，当从栈中出栈一个元素时，检查这个元素与栈顶元素的右子结点是否相同。如果相同，则说明已经完成了左、右子树的遍历。此时，只需要再将栈顶元素出栈一次并输出该结点数据即可。

时间负责度为O(n)，空间复杂度为O(n)。

/**
 * 非递归后序遍历
 * @param root
 */
public void postOrderNonRecursive(BinaryTreeNode root) {
    if (root == null) {
        return;
    }
    Stack<BinaryTreeNode> stack = new Stack<BinaryTreeNode>();
    BinaryTreeNode prev = null; // 记录上一个访问的节点，初始化为null
    BinaryTreeNode current = root; // 当前处理的节点从根节点开始
    while (current != null || !stack.isEmpty()) {
        if (current != null) { // 访问当前节点的左子树和右子树，并将其压入栈中等待处理（但不立即处理）
            stack.push(current);
            current = current.getLeft(); // 先处理左子树（如果有的话）
        } else { // 当前没有左子树或已经处理完左子树，尝试从栈中取出一个节点进行处理（即右子树）
            BinaryTreeNode peekNode = stack.peek(); // 查看栈顶元素（但不弹出）以决定是否处理右子树或根节点
            if (peekNode.getRight() != null && peekNode.getRight() != prev) { // 如果右子树存在且未被访问过，则移动到右子树继续处理（但不立即处理）
                current = peekNode.getRight();
            } else { // 如果右子树已被访问或不存在，处理根节点或回退到上一个节点的右子树的处理（如果有的话）
                System.out.println(stack.pop().getData());
                prev = peekNode; // 更新上一个访问的节点为当前处理的节点（即刚刚处理的根节点）
            }
        }
    }
}

2.9、层次遍历

层次遍历的定义如下：

• 访问根结点。
• 在访问第（层时，将l十1层的结点按顺序保存在队列中。
• 进入下一层并访问该层的所有结点。
• 重复上述操作直至所有层都访问完。

对于上图所示的二叉树，层次遍历产生的输出序列为：1 2 3 4 5 6 7。

时间复杂度为O(n)，空间复杂度为O(n)，因为在最坏情况下，最后一层的所有节点可能同时在队列中。

/**
 * 层次遍历
  * @param root
 */
public void levelOrder(BinaryTreeNode root) {
    BinaryTreeNode temp;
    ArrayDeque<BinaryTreeNode> queue = new ArrayDeque<BinaryTreeNode>();
    if (root == null) {
        return;
    }
    queue.add(root);
    while (!queue.isEmpty()) {
        temp = queue.pop();
        //处理当前节点
        System.out.println(temp.getData());
        if (temp.getLeft() != null) {
            queue.add(temp.getLeft());
        }
        if (temp.getRight() != null) {
            queue.add(temp.getRight());
        }
    }
}

三、二叉树相关问题

3.1、查找二叉树中最大元素

解决此问题的一个简单方法是：利用递归思想，分别找到左子树中的最大元素和右子树中的最大元素，然后将它们与根结点的值进行比较，这3个值中最大的就是问题的解。这个方法利用递归很容易实现。

时间复杂度为O(n)，空间复杂度为O(n)。

/**
 * 查找二叉树中最大元素
  * @param root
 * @return
 */
public int findMax(BinaryTreeNode root) {
    int root_val, left, right, max = Integer.MIN_VALUE;
    if (root != null) {
        root_val = root.getData();
        left = findMax(root.getLeft());
        right = findMax(root.getRight());
        //在三个值中找出最大值
        if (left > right) {
            max = left;
        } else {
            max = right;
        }
        if (root_val > max) {
            max = root_val;
        }
    }
    return max;
}

3.2、非递归查找二叉树中最大值

利用层次遍历方法，在删除结点时观察其数据值是否是最大的。

时间复杂度为O(n)，空间复杂度为O(n)。

/**
 * 非递归查找二叉树中最大元素
 * @param root
 * @return
 */
public int findMaxUsingLevelOrder(BinaryTreeNode root) {
   BinaryTreeNode temp;
   int max = Integer.MIN_VALUE;
   ArrayDeque<BinaryTreeNode> queue = new ArrayDeque<>();
   queue.add(root);
   while (!queue.isEmpty()) {
       temp = queue.pop();
       //所有值中的最大值
       if (max < temp.getData()) {
           max = temp.getData();
       }
       if (temp.getLeft() != null) {
           queue.add(temp.getLeft());
       }
       if (temp.getRight() != null) {
           queue.add(temp.getRight());
       }
   }
   return max;
}

3.3、在二叉树中搜索某个元素

对于给定的二叉树，如果发现树中某结点的数据值与之相同，则返回true。递归地从树的根结点向下，比较左子树与右子树中各个结点的值来实现算法。

时间复杂度为O(n)，空间复杂度为O(n)。

/**
 * 递归搜索二叉中某个元素
 * @param root
 * @param data
 * @return
 */
public boolean findInBinaryTreeUsingRecursion(BinaryTreeNode root, int data) {
    boolean temp;
    //基本情况 == 空树，在此情况下，数据未找到因此返回false
    if(root == null) {
        return false;
    } else {
        //判断是否等于当前根节点的值
        if (data == root.getData()) {
            return true;
        } else {
            //否则从子树继续递归向下搜索
            temp = findInBinaryTreeUsingRecursion(root.getLeft(), data);
            if (temp == true) {
                return temp;
            } else {
                return findInBinaryTreeUsingRecursion(root.getRight(), data);
            }
        }
    }
}

3.4、非递归在二叉树中搜索某个元素

可以利用层次遍历方法来解决这个问题。唯一的不同是在本算法中不是输出数据而是判断根结点的数据是否等于需要搜索元素的值。

时间复杂度为O(n)，空间复杂度为O(n)。

/**
 * 非递归搜索二叉树中的某个元素
 * @param root
 * @param data
 * @return
 */
public boolean searchUsingLevelOrder(BinaryTreeNode root, int data) {
    BinaryTreeNode temp;
    ArrayDeque<BinaryTreeNode> queue = new ArrayDeque<>();
    if (root == null)
        return false;
    queue.add(root);
    while (!queue.isEmpty()) {
        temp = queue.pop();
        //判断是否等于当前根节点的值
        if (data == temp.getData())
            return true;
        if (temp.getLeft() != null)
            queue.add(temp.getLeft());
        if (temp.getRight() != null)
            queue.add(temp.getRight());
    }
    return false;
}

3.5、实现将一个元素插入二叉树中的算法

因为给定的树是二叉树，所以能在任意地方插入元素。为了插人一个元素，可以使用层次遍历方法找到一个左孩子或右孩子结点为空的结点，然后插人该元素。

时间复杂度为O(n)，空间复杂度为O(n)。

/**
 * 将一个元素插入二叉树中
 * @param root
 * @param data
 */
public void insertInBinaryTree(BinaryTreeNode root, int data) {
    ArrayDeque<BinaryTreeNode> queue = new ArrayDeque<>();
    BinaryTreeNode temp;
    BinaryTreeNode newNode = new BinaryTreeNode(data);
    if (root == null) {
        root = newNode;
        return;
    }
    queue.add(root);
    while (!queue.isEmpty()) {
        temp = queue.pop();
        if (temp.getLeft() != null) {
            queue.add(temp.getLeft());
        } else {
            temp.setLeft(newNode);
            return;
        }
        if (temp.getRight() != null) {
            queue.add(temp.getRight());
        } else {
            temp.setRight(newNode);
            return;
        }
    }
}

3.6、获取二叉树节点个数

递归地计算左子树和右子树的大小，再加1（当前结点），然后返回给其双亲结点。

时间复杂度为O(n)，空间复杂度为O(n)。

/**
 * 获取二叉树节点个数
 * @param root
 * @return
 */
public int sizeOfBinaryTree(BinaryTreeNode root) {
    if (root == null)
        return 0;
    else
        return sizeOfBinaryTree(root.getLeft()) + sizeOfBinaryTree(root.getRight()) + 1;
}

3.7、非递归获取二叉树节点个数

利用层次遍历方法。

时间复杂度为O(n)，空间复杂度为O(n)。

/**
 * 非递归获取二叉树节点个数
 * @param root
 * @return
 */
public int sizeOfBinaryTreeUsingLevelOrder(BinaryTreeNode root) {
    BinaryTreeNode temp;
    ArrayDeque<BinaryTreeNode> queue = new ArrayDeque<>();
    int count = 0;
    if (root  == null)
        return 0;
    queue.add(root);
    while (!queue.isEmpty()) {
        temp = queue.pop();
        count++;
        if (temp.getLeft() != null) {
            queue.add(temp.getLeft());
        }
        if (temp.getRight() != null) {
            queue.add(temp.getRight());
        }
    }
    return count;
}

3.8、实现删除数树的算法

为了删除树，需要遍历树的所有结点，然后一个一个地删除它们。但中序遍历、前序遍历、后序遍历以及层次遍历，应该选择哪种遍历方法呢？

在删除双亲结点之前，应该先删除其孩子结点。可以使用后序遍历，在删除过程中不需要存储任何信息。也可以用其他遍历方法删除树，不过需要额外的空间复杂度。下面这棵树的删除顺序为：4,5,2,3,1。

时间复杂度为O(n)，空间复杂度为O(n)。

/**
 * 删除树
 * @param root
 */
public void deleteBinaryTree(BinaryTreeNode root) {
    if (root == null)
        return;
    deleteBinaryTree(root.getLeft());
    deleteBinaryTree(root.getRight());
    //仅当子树删除后再删除当前节点
    root = null;
}

3.9、逆向逐层输出元素

问题9给出算法，逆向逐层输出树中的元素。例如，下图所示二叉树的输出顺序应为：4 5 6 7 2 3 1。

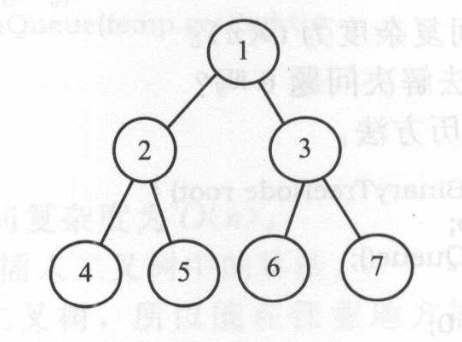
时间复杂度为O(n)，空间复杂度为O(n)。

/**
 * 逆向逐层输出树中元素
 * @param root
 */
public void levelOrderTraversalInReverse(BinaryTreeNode root) {
    ArrayDeque<BinaryTreeNode> queue = new ArrayDeque<>();
    Stack<BinaryTreeNode> stack = new Stack<>();
    BinaryTreeNode temp;
    if (root == null) {
        return;
    }
    queue.add(root);
    while (!queue.isEmpty()) {
        temp = queue.pop();
        if (temp.getRight() != null)
            queue.add(temp.getRight());
        if (temp.getLeft() != null)
            queue.add(temp.getLeft());
        stack.push(temp);
    }
    while (!stack.isEmpty()){
        System.out.println(stack.pop().getData());
    }
}

3.10、求二叉树高度

递归地计算左子树和右子树的高度，然后找出这两棵子树高度中的最大值，再加1，就是树的高度。这类似于前序遍历（或者图的深度优先算法）。

时间复杂度为O(n)，空间复杂度为O(n)。

/**
 * 求二叉树告诉
 * @param root
 * @return
 */
public int heightOfBinaryTree(BinaryTreeNode root) {
    int leftHeight, rightHeight;
    if (root == null) {
        return 0;
    } else {
        leftHeight = heightOfBinaryTree(root.getLeft());
        rightHeight = heightOfBinaryTree(root.getRight());
        if (leftHeight > rightHeight) {
            return leftHeight + 1;
        } else {
            return rightHeight + 1;
        }
    }
}

3.11、非递归求二叉树高度

使用层次遍历算法，这类似于图的广度优先算法。空指针为层次遍历结束的标志。

时间复杂度为O(n)，空间复杂度为O(n)。

/**
 * 非递归计算二叉树告诉
 * @param root
 * @return
 */
public int findHeightOfBinaryTree(BinaryTreeNode root) {
    int level = 1;
    ArrayDeque<BinaryTreeNode> queue = new ArrayDeque<>();
    if (root == null)
        return 0;
    queue.add(null);
    //第一层结束
    while (!queue.isEmpty()) {
        root = queue.pop();
        //当前层遍历结束
        if (root == null) {
            //为下一层增加一个标记
            if (!queue.isEmpty())
                queue.add(null);
            level++;
        } else {
            if (root.getLeft() != null)
                queue.add(root.getLeft());
            if (root.getRight() != null)
                queue.add(root.getRight());
        }
    }
    return level;
}

3.12、查找二叉树中最深节点

时间复杂度为O(n)，空间复杂度为O(n)。

/**
 * 查找二叉树中最深节点
 * @param root
 * @return
 */
public BinaryTreeNode deepestNodeInBinaryTree(BinaryTreeNode root) {
    BinaryTreeNode temp = null;
    ArrayDeque<BinaryTreeNode> queue = new ArrayDeque<>();
    if (root == null)
        return null;
    queue.add(root);
    while (!queue.isEmpty()) {
        temp = queue.pop();
        if (temp.getLeft() != null)
            queue.add(temp.getLeft());
        if (temp.getRight() != null)
            queue.add(temp.getRight());
    }
    return temp;
}

3.13、非递归获取二叉树中叶子节点个数

左孩子结点和右子结点都为空的结点就是叶子结点。

时间复杂度为O(n)，空间复杂度为O(n)。

/**
 * 非递归获取二叉树中叶子节点个数
 * @param root
 * @return
 */
public int numberOfLeavesInBTusingLevelOrder(BinaryTreeNode root) {
    BinaryTreeNode temp;
    ArrayDeque<BinaryTreeNode> queue = new ArrayDeque<>();
    int count = 0;
    if (root == null)
        return 0;
    queue.add(root);
    while (!queue.isEmpty()) {
        temp = queue.pop();
        if (temp.getLeft() == null && temp.getRight() == null) {
            count++;
        } else {
            if (temp.getLeft() != null)
                queue.add(temp.getLeft());
            if (temp.getRight() != null)
                queue.add(temp.getRight());
        }
    }
    return count;
}

3.14、非递归查找二叉树中满节点个数

既有左孩子结点，又有右孩子结点的结点叫作满结点，这些结点的个数就是问题的解。

时间复杂度为O(n)，空间复杂度为O(n)。

/**
 * 非递归查找二叉树中满节点个数
 * @param root
 * @return
 */
public int numberOfFullNodesInBTusingLevelOrder(BinaryTreeNode root) {
    BinaryTreeNode temp;
    ArrayDeque<BinaryTreeNode> queue = new ArrayDeque<>();
    int count = 0;
    if (root == null)
        return 0;
    queue.add(root);
    while (!queue.isEmpty()) {
        temp = queue.pop();
        if (temp.getLeft() != null && temp.getRight() != null) {
            count++;
        }
        if (temp.getLeft() != null)
            queue.add(temp.getLeft());
        if (temp.getRight() != null)
            queue.add(temp.getRight());
    }
    return count;
}

3.15、非递归查找二叉树中的半节点

半结点就是只有左孩子结点或者只有右孩子结点的结点，半结点只能有一个孩子结点。

时间复杂度为O(n)，空间复杂度为O(n)。

/**
 * 非递归查找二叉树中的半节点
 * @param root
 * @return
 */
public int numberOfHalfNodesInBTusingLevelOrder(BinaryTreeNode root) {
    BinaryTreeNode temp;
    ArrayDeque<BinaryTreeNode> queue = new ArrayDeque<>();
    int count = 0;
    if (root == null)
        return 0;
    queue.add(root);
    while (!queue.isEmpty()) {
        temp = queue.pop();
        if ((temp.getLeft() != null && temp.getRight() == null) ||
                (temp.getLeft() == null && temp.getRight() != null)) {
            count++;
        }
        if (temp.getLeft() != null)
            queue.add(temp.getLeft());
        if (temp.getRight() != null)
            queue.add(temp.getRight());
    }
    return count;
}

3.16、判断两颗二叉树结构是否相同

• 如果两棵树都为空树，则返回true。
• 如果两棵树都不为空，则比较数据并递归地判断左子树与右子树是否相同。

时间复杂度为O(n)，空间复杂度为O(n)。

/**
 * 判断两颗二叉树结构是否相同
 * @param root1
 * @param root2
 * @return
 */
public boolean areStructurullySameTrees(BinaryTreeNode root1, BinaryTreeNode root2) {
    if (root1 == null && root2 == null)
        return true;
    if (root1 == null || root2 == null)
        return false;
    return (root1.getData() == root2.getData()) &&
            areStructurullySameTrees(root1.getLeft(), root2.getLeft()) &&
            areStructurullySameTrees(root1.getRight(), root2.getRight());
}

3.17、求二叉树直径

求二叉树直径的算法。树的直径（有时也叫作树的宽度）就是树中两个叶子结点之间的最长路径中的结点个数。

为了获取树的直径，首先需要递归地计算左子树的直径和右子树的直径。找出两者中最大值，再加1返回。

时间复杂度为O(n)，空间复杂度为O(n)。

/**
 * 求二叉树的宽度
 * @param root
 * @param diameter
 * @return
 */
public int diameterOfTree(BinaryTreeNode root, int diameter) {
    int left, right;
    if (root == null)
        return 0;
    left = diameterOfTree(root.getLeft(), diameter);
    right = diameterOfTree(root.getRight(), diameter);
    if (left + right > diameter)
        diameter = left + right;
    return Math.max(left, right) + 1;
}

3.18、求二叉树同一层节点数据之和最大的层

逻辑上类似于查找二叉树的层数。唯一不同的是，还需要跟踪每一层结点的数据和。

时间复杂度为O(n)，空间复杂度为O(n)。

/**
 * 求二叉树同一层节点数据之和最大的层
 * @param root
 * @return
 */
public int findLevelWithMaxSum(BinaryTreeNode root) {
    BinaryTreeNode temp;
    int level = 0, maxLevel = 0;
    ArrayDeque<BinaryTreeNode> queue = new ArrayDeque<>();
    int currentSum = 0, maxSum = 0;
    if (root == null)
        return 0;
    queue.add(root);
    queue.add(null);//第一次结束
    while (!queue.isEmpty()) {
        temp = queue.pop();
        //若当前层遍历完成则比较和
        if (temp == null) {
            if (currentSum > maxSum) {
                maxSum = currentSum;
                maxLevel = level;
            }
            currentSum = 0;
            //将标记下一层结束的指示器置入队尾
            if (!queue.isEmpty())
                queue.add(null);
            level++;
        } else {
            currentSum += temp.getData();
            if (temp.getLeft() != null)
                queue.add(temp.getLeft());
            if (temp.getRight() != null)
                queue.add(temp.getRight());
        }
    }
    return maxLevel;
}

3.19、输出所有从根节点到叶子节点的路径

时间复杂度为O(n)。空间复杂度为O()上的所有结点，用于栈递归。

/**
 * 输出所有从根节点到叶子节点的路径
 * @param root
 */
public void printPaths(BinaryTreeNode root) {
    int[] path = new int[256];
    printPaths(root, path, 0);
}

private void printPaths(BinaryTreeNode node, int[] path, int pathLen) {
    if (node == null)
        return;
    //将该节点添加到路径数组中
    path[pathLen] = node.getData();
    pathLen++;
    //当前为叶子节点，因此输出到这里的路径
    if (node.getLeft() == null && node.getRight() == null) {
        printArray(path, pathLen);
    } else {
        //否则，继续遍历两颗子树
        printPaths(node.getLeft(), path, pathLen);
        printPaths(node.getRight(), path, pathLen);
    }
}

private void printArray(int[] paths, int pathLen) {
    for (int i = 0; i < pathLen; i++) {
        System.out.printf(paths[i] + " ");
    }
    System.out.println();
}

1 2 4 
1 2 5 
1 3 6 
1 3 7 

3.20、判断是否存在路径的数据和等于给定值

给出一个算法，判断是否存在路径的数据和等于给定值。也就是说，判断是否存在一条从根结点到任意结点的路径，其所经过结点的数据和为给定值。

对这个问题的策略是：递归地实现如下步骤，在调用其孩子结点之前，先把sum值减去该结点的值。然后在运行过程中检查sum值是否为0。

时间复杂度为O(n)，空间复杂度为O(n)。

/**
 * 判断是否存在路径的数据和等于给定值
 * @param root
 * @param sum
 * @return
 */
public boolean hasPathSum(BinaryTreeNode root, int sum) {
    if (root == null)
        return sum == 0;
    else {
        int subSum = sum - root.getData();
        return hasPathSum(root.getLeft(), subSum) || hasPathSum(root.getRight(), subSum);
    }
}

3.21、二叉树镜像转换

实现将一棵树转换为其镜像的算法。树的镜像是指相互交换非叶子结点的左子树、右子树，得到的另一棵树。下面的两棵树就互为镜像。

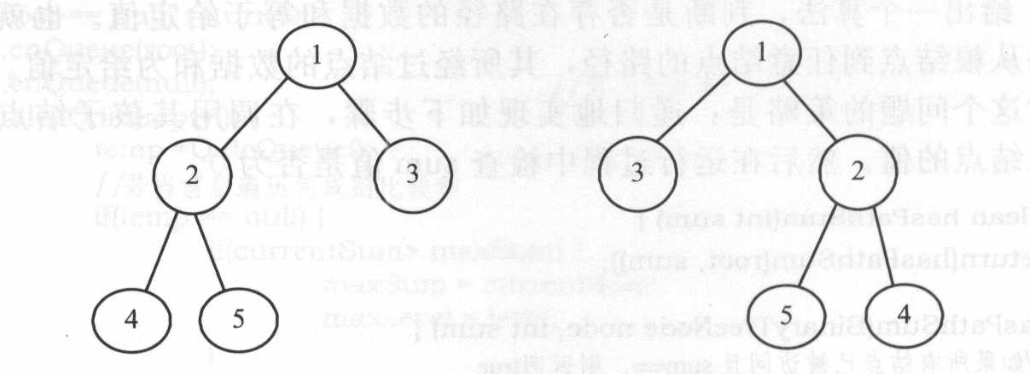
时间复杂度为O(n)，空间复杂度为O(n)。

/**
 * 镜像
 * @param root
 * @return
 */
public BinaryTreeNode mirrorOfBinaryTree(BinaryTreeNode root) {
    BinaryTreeNode temp;
    if (root != null) {
        mirrorOfBinaryTree(root.getLeft());
        mirrorOfBinaryTree(root.getRight());
        //交换节点的两个指针
        temp = root.getLeft();
        root.setLeft(root.getRight());
        root.setRight(temp);
    }
    return root;
}

3.21、判断两颗二叉树是否互为镜像

时间复杂度为O(n)，空间复杂度为O(n)。

/**
 * 判断两颗二叉树是否互为镜像
 * @param root1
 * @param root2
 * @return
 */
public boolean areMirrors(BinaryTreeNode root1, BinaryTreeNode root2) {
    if (root1 == null && root2 == null)
        return true;
    if (root1 == null || root2 == null)
        return false;
    if (root1.getData() != root2.getData())
        return false;
    else
        return areMirrors(root1.getLeft(), root2.getRight()) &&
                areMirrors(root1.getRight(), root2.getLeft());

3.22、根据中序和前序遍历构建二叉树

考虑以下遍历序列：

• 中序序列：D B E A F C
• 前序序列：A B D E C F

在前序序列中，最左边的元素是树的根结点。所以A是给定序列的根。通过在中序序列中找到'A',能够找到'A'左边的所有元素，它们来自左子树，也能找到'A'右边的所有元素，它们来自右子树。因此可以得出如下的二叉树。

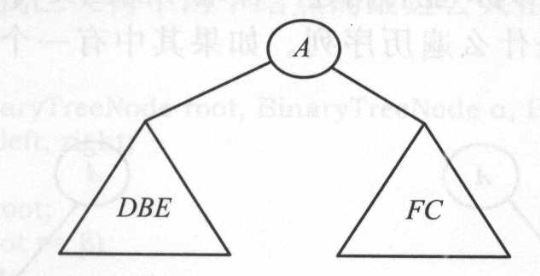
基于以上步骤，可以递归地得到如下二叉树:

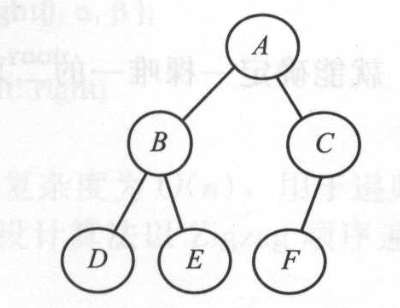
算法：BuildTree()。

1. 从前序序列中取一个元素，将前序索引变量（下面代码中的preIndex)加1，用于选取下一次递归调用时的元素。
2. 根据选择元素的数据值，创建一个新的树结点(newNode)。
3. 查找所选结点在中序序列中的索引，用变量inIndex标记。
4. 调用BuildBinary Tree为inIndex之前的所有结点构建一棵子树，将其作为newNode结点的左子树。
5. 调用BuildBinaryTree为inIndex之后的所有结点构建一棵子树，将其作为newNode结点的右子树。
6. 返回newNode。前家

/**
 * 根据前序和中序遍历构建二叉树
 * @param inorder 中序序列
 * @param preorder 前序序列
 * @return
 */
public BinaryTreeNode buildTree(int[] preorder, int[] inorder) {
    if (preorder == null || inorder == null || preorder.length != inorder.length) {
        return null;
    }
    return buildTreeHelper(preorder, 0, preorder.length - 1, inorder, 0, inorder.length - 1);
}

private BinaryTreeNode buildTreeHelper(int[] preorder, int preStart, int preEnd, int[] inorder, int inStart, int inEnd) {
    if (preStart > preEnd || inStart > inEnd) {
        return null;
    }

    // 前序遍历的第一个元素是根节点
    BinaryTreeNode root = new BinaryTreeNode(preorder[preStart]);
    int rootIndexInInorder = 0; // 找到根节点在中序遍历中的位置
    for (int i = inStart; i <= inEnd; i++) {
        if (inorder[i] == root.getData()) {
            rootIndexInInorder = i;
            break;
        }
    }

    // 递归构建左子树和右子树
    root.setLeft(buildTreeHelper(preorder, preStart + 1, preStart + rootIndexInInorder - inStart, inorder, inStart, rootIndexInInorder - 1));
    root.setRight(buildTreeHelper(preorder, preStart + rootIndexInInorder - inStart + 1, preEnd, inorder, rootIndexInInorder + 1, inEnd));
    return root;
}

3.23、查找二叉树中两个节点的最近公共祖先

/**
 * 查找二叉树中两个节点的最近公共节点 LCA
 * @param root
 * @param a
 * @param b
 * @return
 */
public BinaryTreeNode lca(BinaryTreeNode root, BinaryTreeNode a, BinaryTreeNode b) {
    BinaryTreeNode left, right;
    if (root == null || root == a || root == b)
        return root;
    left = lca(root.getLeft(), a, b);
    right = lca(root.getRight(), a, b);
    if (left != null && right != null)
        return root;
    else
        return left != null ? left : right;
}