【复杂网络分析】如何入门Louvain算法？

引言

在图挖掘领域，社区发现（Community Detection） 是核心任务之一，它用于挖掘图中内部连接紧密、外部连接稀疏的节点集合（即"社区"）。无论是社交网络的用户分组、生物网络的功能模块识别，还是推荐系统的兴趣聚类，社区发现都有着广泛的应用。

在众多社区发现算法中，Louvain算法凭借其高效性和优异的划分效果脱颖而出，尤其适合处理大规模无向图。本文将从原理到实战，手把手教你入门Louvain算法，附带完整Python代码，新手也能快速上手！

一、Louvain算法核心基础

1.1 核心目标：最大化模块度（Modularity）

Louvain算法的核心优化目标是模块度（Modularity，记为Q），这是一个衡量社区划分质量的量化指标，用于描述"社区内部边数"与"随机情况下期望内部边数"的差异程度。

模块度的计算公式如下（针对无向图）：
Q = 1 2 m ∑ i , j ( A i j − k i k j 2 m ) δ ( c i , c j ) Q = \frac{1}{2m} \sum_{i,j} \left( A_{ij} - \frac{k_i k_j}{2m} \right) \delta(c_i, c_j) Q=2m1i,j∑(Aij−2mkikj)δ(ci,cj)

其中各参数的通俗解释：

m m m：图中所有边的总数量
A i j A_{ij} Aij：节点 i i i和节点 j j j之间的邻接矩阵值（有边为1，无边为0）
k i k_i ki：节点 i i i的度（连接的边数）
c i c_i ci：节点 i i i所属的社区标签
δ ( c i , c j ) \delta(c_i, c_j) δ(ci,cj)：指示函数，若 c i = c j c_i = c_j ci=cj（两节点同社区）则为1，否则为0
1 2 m \frac{1}{2m} 2m1：归一化系数，确保 Q Q Q的取值范围在 [ − 1 , 1 ] [-1, 1] [−1,1]之间

模块度 Q Q Q的核心意义：

Q > 0 Q > 0 Q>0：说明社区内部连接比随机分布更紧密，划分有效
Q Q Q越大（通常在 0.3 ∼ 0.7 0.3 \sim 0.7 0.3∼0.7之间）：社区划分质量越好
Q < 0 Q < 0 Q<0：划分效果不如随机分布

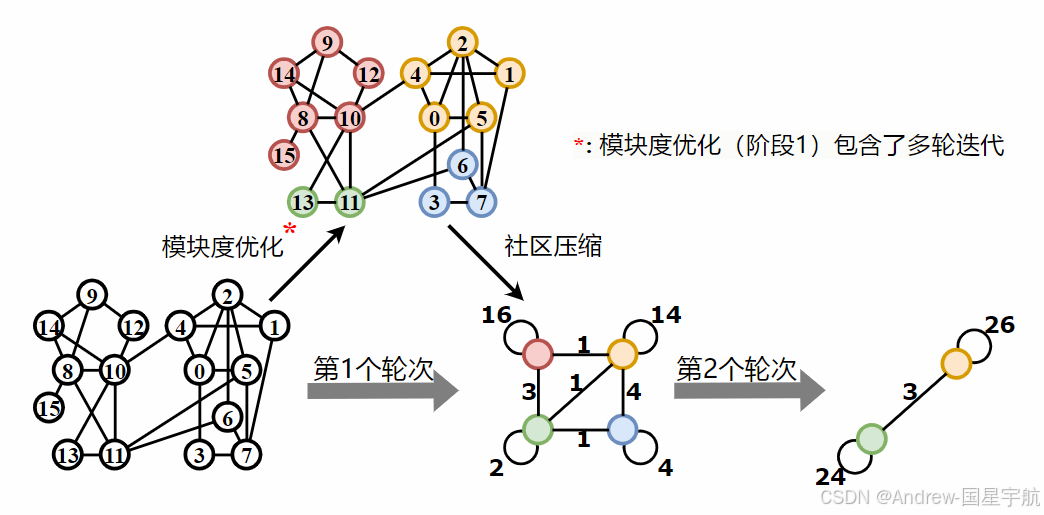
1.2 核心流程：两阶段迭代

Louvain算法采用"局部优化+层级压缩"的迭代策略，分为两个核心阶段，重复执行直到模块度不再提升。

阶段1：局部社区优化（节点迁移）

该阶段的目标是对每个节点进行局部调整，最大化模块度增益，步骤如下：

初始化：将每个节点视为一个独立的社区（即每个节点自身就是一个社区）
遍历每个节点 u u u，依次尝试将 u u u迁移到其每个邻居节点 v v v所属的社区中
计算每次迁移带来的模块度增益 Δ Q \Delta Q ΔQ ，选择使 Δ Q \Delta Q ΔQ最大的社区（若最大 Δ Q > 0 \Delta Q > 0 ΔQ>0，则执行迁移；否则不迁移）
重复步骤2-3，直到遍历所有节点后，没有节点能通过迁移提升模块度，阶段1终止

阶段2：社区压缩（构建超级节点）

该阶段的目标是将阶段1得到的社区进行"压缩"，构建新图以便后续迭代优化，步骤如下：

将阶段1中每个独立的社区合并为一个超级节点（Super Node）
新图中，超级节点之间的边权重 = 原社区之间所有节点对的边数之和
新图中，超级节点的自环权重 = 原社区内部所有边数的2倍（无向图边需双向计算）
以新构建的压缩图作为输入，重新执行阶段1，开始下一轮迭代

整体迭代逻辑

重复"阶段1（局部优化）→ 阶段2（社区压缩）"的流程，直到某次迭代后模块度不再提升，算法终止，最终得到的社区划分即为最优结果。

二、Louvain算法优势

时间复杂度低 ：近似 O ( n log ⁡ n ) O(n \log n) O(nlogn)（ n n n为节点数），远优于传统的谱聚类等算法，可轻松处理十万甚至百万级节点的大规模图
实现简单：核心逻辑清晰，依赖库成熟，新手容易上手
效果优异：在多数实际场景（社交网络、生物网络等）中，划分质量优于同类轻量级算法
支持无向加权图：对加权图有良好的兼容性，可处理边带有权重的场景（如社交网络中的互动频率）

三、实战环节：Python实现Louvain社区发现

接下来我们通过Python代码实战Louvain算法，使用经典的"空手道俱乐部图"进行演示，步骤清晰，代码可直接复制运行。

3.1 环境准备

首先安装所需依赖库：

networkx：用于图的构建、操作和可视化
python-louvain：Louvain算法的成熟实现（注意：避免直接安装community库，存在重名冲突）
matplotlib：用于结果可视化

安装命令：

bash 复制代码

pip install networkx python-louvain matplotlib

3.2 完整可运行代码

python 复制代码

# 导入所需库
import networkx as nx
import community as community_louvain
import matplotlib.pyplot as plt
import matplotlib.cm as cm

def louvain_community_detection_demo():
    # 步骤1：加载/构建示例图（空手道俱乐部图，经典社区发现测试集）
    # 该图描述了一个空手道俱乐部的34名成员之间的社交关系，因俱乐部主任和教练的矛盾，最终分裂为两个社区
    G = nx.karate_club_graph()
    print(f"图的节点数：{G.number_of_nodes()}")
    print(f"图的边数：{G.number_of_edges()}")

    # 步骤2：运行Louvain算法，获取社区划分结果
    # partition是一个字典，key为节点ID，value为社区标签（整数类型）
    partition = community_louvain.best_partition(G)
    print(f"\n最终划分的社区数量：{len(set(partition.values()))}")

    # 步骤3：计算并输出最终模块度（评估划分质量）
    modularity = community_louvain.modularity(partition, G)
    print(f"最终模块度Q：{modularity:.4f}")

    # 步骤4：可视化社区划分结果
    # 设置画布大小
    plt.figure(figsize=(10, 8))
    # 计算图的布局（spring_layout：力导向布局，更美观）
    pos = nx.spring_layout(G, seed=42)  # seed固定随机种子，确保布局可复现

    # 为每个社区分配不同的颜色
    cmap = cm.get_cmap('viridis', max(partition.values()) + 1)
    # 绘制节点：根据社区标签分配颜色
    nx.draw_networkx_nodes(G, pos, partition.keys(), node_size=500,
                           cmap=cmap, node_color=list(partition.values()))
    # 绘制边
    nx.draw_networkx_edges(G, pos, alpha=0.3)
    # 绘制节点标签（节点ID）
    nx.draw_networkx_labels(G, pos, font_size=12, font_family='sans-serif')

    # 设置标题和关闭坐标轴
    plt.title(f'Louvain算法社区划分结果（模块度Q={modularity:.4f}）', fontsize=14)
    plt.axis('off')
    # 显示图形
    plt.show()

    # 步骤5：输出每个节点的社区标签
    print("\n节点-社区标签映射：")
    for node, comm in sorted(partition.items()):
        print(f"节点{node:2d} → 社区{comm}")

if __name__ == "__main__":
    louvain_community_detection_demo()

3.3 代码运行结果说明

基础信息输出：
- 空手道俱乐部图包含34个节点、78条边
- 最终划分出2个社区（与真实场景一致，俱乐部分裂为两派）
- 模块度Q约为0.3717（大于0，说明划分有效，质量良好）
可视化结果：
- 不同颜色的节点对应不同社区
- 节点间的边清晰展示了社区内部连接紧密、外部连接稀疏的特点
- 力导向布局让社区划分的视觉效果更直观
节点-社区映射：
- 输出按节点ID排序的社区标签，可清晰看到每个节点的归属
- 例如节点0（俱乐部主任）和节点33（教练）分别属于两个不同社区，符合真实场景

四、进阶：处理自定义图数据

上述示例使用了内置的空手道俱乐部图，实际应用中我们常需要处理自定义数据（如边列表文件），以下是处理自定义无向图的代码片段：

python 复制代码

def louvain_custom_graph_demo():
    # 步骤1：构建自定义图（从边列表文件读取，或手动添加边）
    G = nx.Graph()
    # 方式1：手动添加边
    edges = [(0,1), (0,2), (1,2), (1,3), (2,3), (3,4), (4,5), (4,6), (5,6)]
    G.add_edges_from(edges)

    # 方式2：从边列表文件读取（文件格式：每行两个节点ID，用空格分隔）
    # G = nx.read_edgelist("custom_edges.txt")

    # 步骤2：运行Louvain算法
    partition = community_louvain.best_partition(G)
    modularity = community_louvain.modularity(partition, G)

    # 步骤3：可视化（同上述示例，此处省略重复代码）
    print(f"自定义图社区数量：{len(set(partition.values()))}")
    print(f"自定义图模块度：{modularity:.4f}")

if __name__ == "__main__":
    # 运行自定义图演示
    louvain_custom_graph_demo()

五、总结

核心知识点回顾：
- Louvain算法的核心是最大化模块度，通过"局部社区优化+社区压缩"两阶段迭代实现
- 模块度Q是衡量社区划分质量的关键指标，取值范围 [ − 1 , 1 ] [-1,1] [−1,1]， Q > 0 Q>0 Q>0表示划分有效
- Louvain算法的优势是高效、简单、效果好，支持大规模图
实战关键要点：
- 依赖库安装：需安装python-louvain（而非community）
- 核心函数：community_louvain.best_partition()（执行算法）、community_louvain.modularity()（计算模块度）
- 可视化：通过networkx和matplotlib可直观展示社区划分结果
应用场景拓展：
- 社交网络：用户兴趣分组、好友推荐
- 生物信息学：蛋白质相互作用网络的功能模块识别
- 信息传播：舆情传播路径分析、谣言溯源
- 推荐系统：基于社区的商品/内容推荐

后续学习建议

深入理解模块度的数学推导，掌握加权图的模块度计算方式
对比Louvain算法与其他社区发现算法（如GN算法、谱聚类、Infomap算法）
尝试基于Louvain算法解决实际问题（如分析微博用户社交网络、论文引用网络的社区划分）