SVM（支持向量机算法）
1.SVM算法介绍
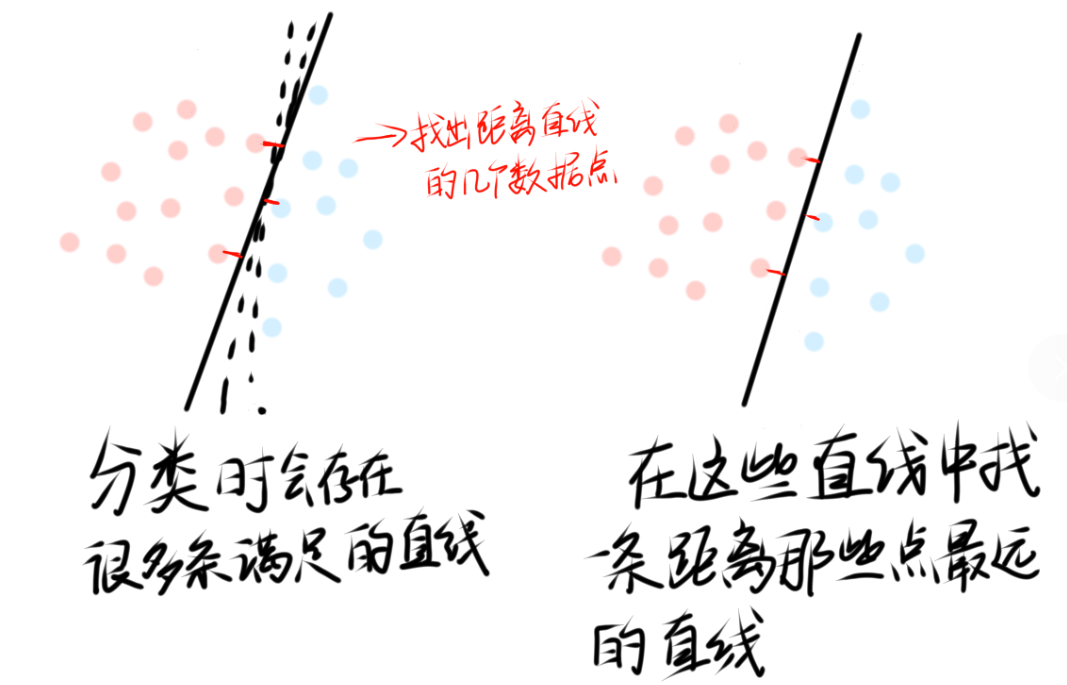
默认是用于分类，核心就是找最佳分割线或是超平面
过程：对于一个分类问题svm算法是找出最优的直线，除了能分开类别之外，这里还有两个变量是相互制约的，也就是我们要根据直线找出距离最近的数据点，同时这条直线要离这些数据点距离是最远的，很类似于数学中双变量的问题
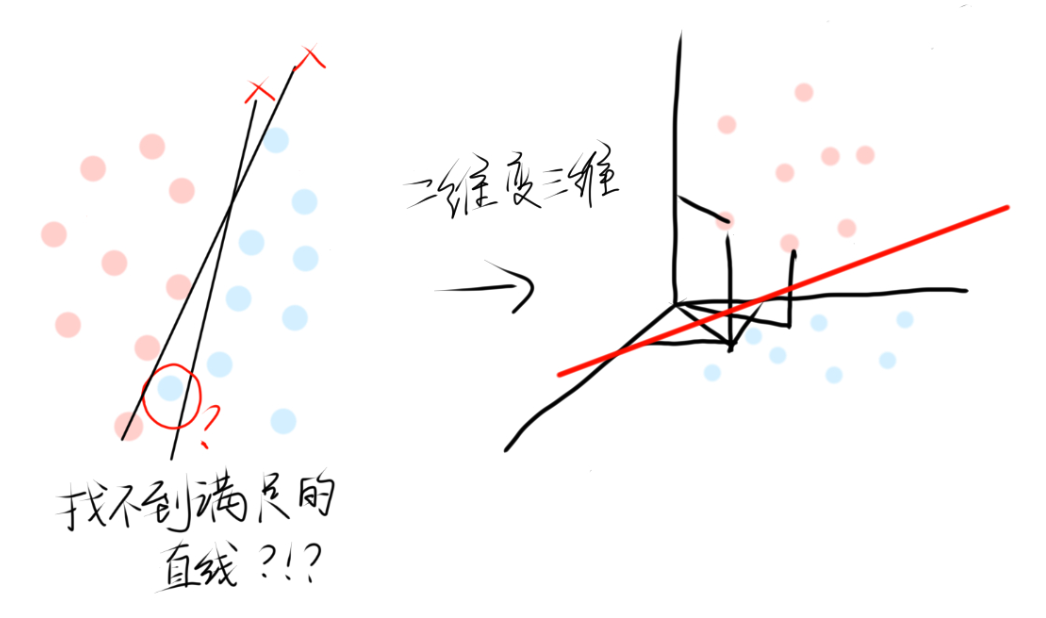
上面是比较简单的二分类，如果这里我们的数据更加复杂，无法找到一条直线分类，那就使用svm算法最特别的一点------升维。
举一个例子，将二维数据映射到三维空间，在三维空间中就能找到一个平面（对应二维的一条直线）完美的进行分类，这里也是有两个变量相互制约的。
关于为什么升维就可以划分类别，其实这个问题很简单，可以把二维图看成是三维图的俯视图，二维时看似已经找不到合适的直线，但构造出三维后，就可以找到合适的直线（超平面），这里涉及到的是数学的空间问题。
虽然svm和逻辑回归都是处理分类问题的，但两者有很大区别，逻辑回归是概率拟合，使用到了sigmoid函数，看最后概率接近哪边就归类到哪一类，svm与之不同就是，svm追求最大间隔，也就是要找到最优的直线（超平面）并且可以把数据升维。
对于svm涉及双变量的问题涉及到了萨格朗日乘子法等数学方法，推导比较复杂，这里就不详细讲述。
2.软间隔
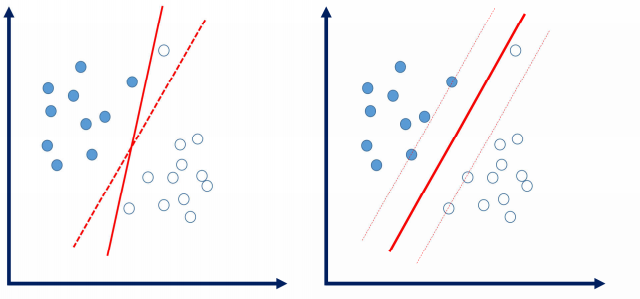
如果我们本来拟合的直线因为一个异常数据而改变了，那我们拟合的直线可能就不太准确了，如果让这些异常数据不影响我们的直线拟合呢？我们可以在直线周围设置一个'缓冲区'，在缓冲区中的数据不影响我们的直线拟合。
1）软间隔的含义
数据中存在一些噪音点，如果考虑这些噪音点的话，直线（超平面）可能表现得效果不好，而出现过拟合的现象，我们允许个别异常样本点出现在间隔带中。
2）松弛因子
该异常数据点与它原本应该在的位置之间的函数间隔差值就叫松弛因子**ξ，**并不是简单的一个距离，是函数差值。
上述我们讲过svm算法有两个变量相互制约，且省去了其中复杂的数学公式推导，
，这个式子就是我们经过推导所得到的，意思是数据点要在某一侧，且距离直线（超平面）距离至少为1（为什么为1，是因为无论平面还是空间，所构造的平面坐标或者空间坐标系的刻度都是可规定的，也就相当于把间隔归一化处理了，这个也是一种数学方法）
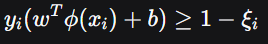，这个就是软间隔的约束条件，软间隔就是一个允许违规的分类机制，松弛因子用于量化违规程度的变量。
通俗点说，如果软间隔是一条允许车压线的规则，但是压线不能超过ξ米，松弛因子就是这个程度。
3）c参数
式子可以不用深究，我们就把软间隔的存在当作一个错误数据的缓冲区，一个容错空间，与此同时我们也要对软间隔进行约束，不能让所有数据都在软间隔里，也不能让有异常的数据在软间隔外。
c值的引出是用来管制松弛因子的，c值在svm算法中是一个可直接调节的参数，通过调节c值就可以控制松弛因子的大小。c值越大，松弛因子总体水平变小，分类越严格。所以我们希望有松弛因子是要处理一些异常数据对直线拟合的影响，让直线拟合'松一些'。同时我们又希望松弛因子小，使我们分类严格一些，看似矛盾的两个要求实际上是不矛盾的，而是找到平衡点，能让模型得到更好的训练。
对于上述目标函数的变更（加入c值），我们依旧是需要数学推导对目标函数进行求解，也是用到萨格朗日乘子法，也不做叙述。
3.升维
1）核函数
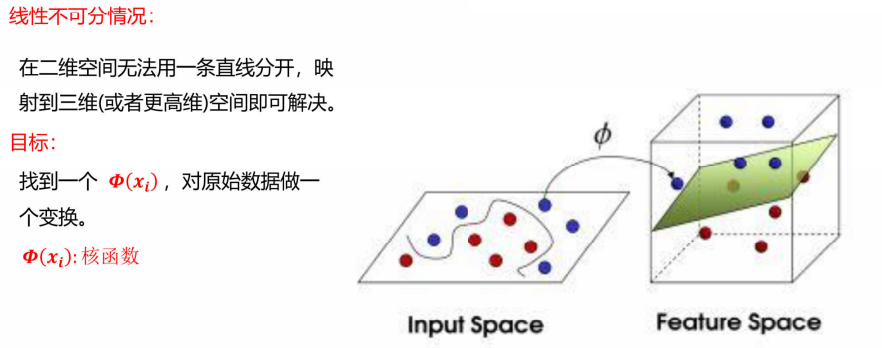
2）常用的核函数
- 线性核函数
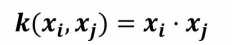
- 多项式核函数
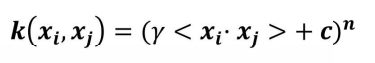
- 高斯核函数
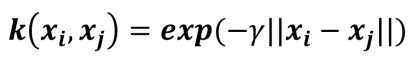
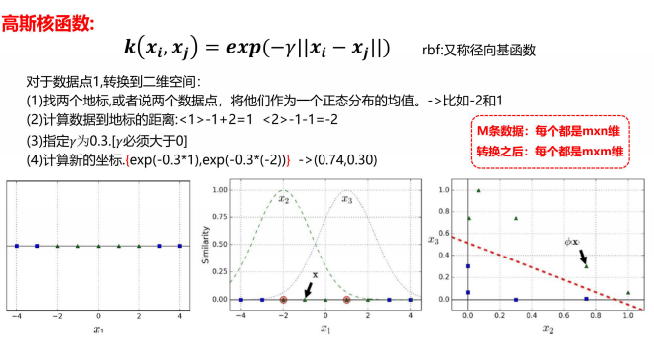
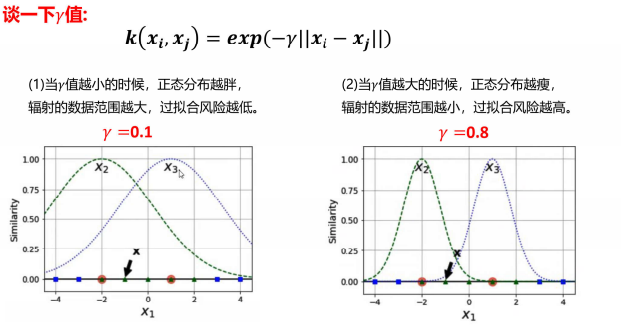
4.svm优缺点
随机森林适合多数据，数据少反而不行，svm数据少效果越好
5.svm算法的实现
svm中有很多可调节的参数其中重要的有C，kernel，degree，gamma
我们对先前使用过的垃圾邮件数据
python
import pandas as pd
import numpy as np
from sklearn import metrics
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
data=pd.read_csv(r"D:\learn\代码所用文本\spambase.csv")
'''使用svm进行训练'''
from sklearn.svm import LinearSVC
X=data.iloc[:,:-1]
Y=data.iloc[:,-1]
scaler = StandardScaler()
X = scaler.fit_transform(X)
x_train, x_test, y_train, y_test = train_test_split\
(X, Y, test_size=0.3, random_state=0)
from sklearn.model_selection import cross_val_score
scores =[]
c_s =[0.01,0.1,1,10,100,1000]#参数
for i in c_s:
svm = LinearSVC(C=i,random_state=0)
score = cross_val_score(svm,x_train, y_train, cv=5,scoring='recall')#交叉验证
score_mean=sum(score)/len(score)
scores.append(score_mean)
print(score_mean)
best_c= c_s[np.argmax(scores)]
print('最优C值：{}'.format(best_c))
svm = LinearSVC(C=best_c, random_state=0)
svm.fit(X, Y)
train_pre=svm.predict(x_train)
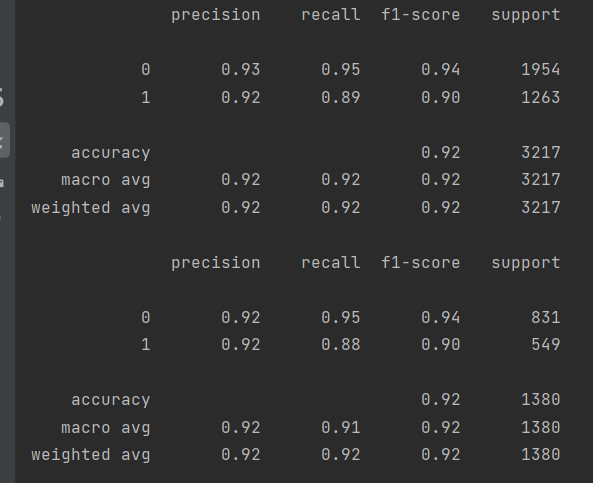
print(metrics.classification_report(y_train,train_pre))
train_pre=svm.predict(x_test)
print(metrics.classification_report(y_test,train_pre))