强化学习笔记

基本概念

强化学习中涉及的基本概念：

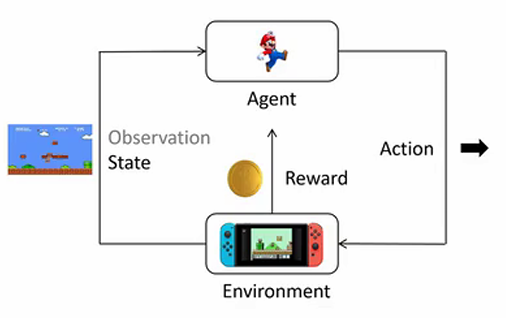
• **环境 (Environment)：**环境是智能体所处的外部系统，它负责产生当前的状态，接收智能体的动作并返回新的状态和对应的奖励。环境的作用相当于模拟现实中的条件和反应规则，智能体只能通过与环境的交互来了解其动态变化。
• **智能体 (Agent)：**智能体是强化学习中的决策者，它会不断地观察环境的状态，并根据其策略选择动作。智能体的目标是通过选择一系列最优动作，获得尽可能多的累积奖励。
• **状态 (State)：**状态是环境在特定时刻的全面描述。对于智能体而言，状态是决策的基础，它包含了关于当前环境的所有重要信息。
• **动作 (Action)：**动作是智能体对当前状态的反应。基于当前的状态，智能体使用其策略函数来决定下一步要采取的动作。
• **奖励 (Reward)：**奖励是环境对智能体执行动作后给予的反馈。奖励可以是正的（奖励）或者负的（惩罚）。例如，在超级马里奥游戏中，吃到金币可以获得正奖励（例如 +10 分），而碰到敌人会得到负奖励（例如 -100 分）。
• **动作空间 (Action Space)：**指智能体在当前状态下可以选择的动作集合。
• 轨迹 (Trajectory)： 轨迹（又称为回合或 episode）是指智能体在一次完整的交互过程中经历的一系列状态、动作和奖励的序列。轨迹通常表示为 ，其中 表示第 i 时刻的状态， 表示智能体在状态 下选择的动作。。比如大语言模型生成时，它的状态就是已经生成的 token 序列。当前的动作是生成下一个 token. 当前 token 生成后，已生成的序列就加上新生成的 token 成为下一个状态。
• 回报 (Return Reward)： 表示从当前时间步开始直到未来的累积奖励和，通常用符号 表示：. 回报的定义是智能体决策的重要依据，因为强化学习的目标是训练一个策略，使得智能体在每个状态下的期望回报最大化。

目标

在强化学习中，目标是训练一个神经网络 Policy ，在所有状态 s 下，给出相应的 Action，得到的 Return 的期望值最大。即：

其中：

• ：表示在策略 下轨迹 的回报 的期望值。
• ：轨迹 的回报，即从起始状态到终止状态获得的所有奖励的总和。
• ：表示一条轨迹，即智能体在环境中的状态和动作序列。
• ：在参数 θ 下生成轨迹 的概率，通常由策略或策略网络确定。
• θ：策略的参数，控制着策略 的行为。

所以，我们的目标是找到一个策略 ，使得 最大。那怎么找到这个策略呢？我们使用梯度上升的办法，即不断地更新策略参数 θ，使得 不断增大。

首先，我们来计算梯度：

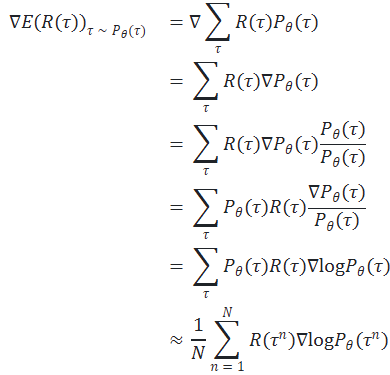
接下来，我们来看一下 Trajectory 的概率 是怎么计算的：

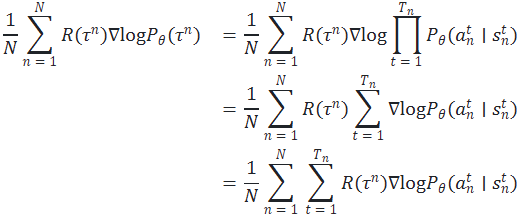
• ：对轨迹 的概率对数进行求导，表示利用策略梯度对期望回报进行优化。

• ：表示轨迹 中所有步骤 上采取的动作 在状态 下的联合概率。

• ：利用对数的可加性，将联合概率的对数梯度分解为各步的对数梯度之和。

• ：对每一步动作的概率对数取梯度，分解为每一步的累加。

• ：利用累积回报 加权每一步的对数梯度，体现策略梯度方法中的优势估计。

这个梯度的展开结果直接去掉梯度符号就对应前面的期望的展开结果，即目标函数：

这个式子表示如果当前的 Trajectory 的回报 较大，那么我们就会增大这个 Trajectory 下所有 action 的概率，反之亦然。我们后面的变形都是针对目标梯度的，要将其变回目标函数只需要去掉梯度符号即可。

那我们应该如何训练一个 Policy 网络呢？根据前面的期望我们可以定义loss函数为：

在我们的目标函数前加上负号，就可以转化为一个最小化问题。我们可以使用梯度下降的方法来求解这个问题。

这样，我们就可以不断地调整策略，使得回报最大化。但这明显是存在改进空间的，因为我们要判断是否增大或减小在状态 s 下采取动作 a 的概率，不应该看整个 trajectory 的累计回报，而应该只看采取这个动作后到游戏结束的累计回报。另外一个动作对接下来的回报产生的影响应该会随着步数越往后越小。

针对这个问题，我们修改一下公式：

其中：

• ：轨迹 的累积回报，这里使用了未来回报的折扣求和来表示。

• ：从时间步 开始的未来折扣回报。

• ：对时间步 到 (轨迹结束时刻) 之间的所有奖励进行求和。

• ：折扣因子 的幂次，控制未来奖励的权重，. 当 越远离当前时刻 t，其贡献越小。

• ：在时间步 发生的即时奖励。

总的来说，修改后的公式是对未来回报的折扣求和。

还有一种情况会影响我们算法的稳定性，那就是在好的局势下和坏的局势下。比如在好的局势下，不论你做什么动作，你都会得到正的回报，这样算法就会增加所有动作的概率。 得到 reward 大的动作的概率大一些，但是这样会让训练很慢，也会不稳定。最好是能够让相对好的动作的概率增加，相对坏的动作的概率减小。

为了解决这个问题，我们可以对所有动作的 reward 都减去一个 baseline，这样就可以让相对好的动作的reward增加，相对坏的动作的 reward 减小，也能反映这个动作相对其他动作的价值。

所以我们的目标梯度就变为：

其中， 也需要用神经网络来拟合，这就是我们的 Actor-Critic 网络。Actor 网络负责输出动作的概率，Critic 网络负责评估 Actor 网络输出的动作好坏。

接下来我们再来解释几个常见的强化学习概念：

• Action-Value Function： 每次都是随机采样，方差很大，我们可以用 来代替， 表示在状态 s 下采取动作 a 的价值，即从状态 s 开始，采取动作 a 后，按照某个策略 π 执行，最终获得的回报的期望值。 可以用来评估在状态 s 下采取动作 a 的好坏，从而指导智能体的决策，即动作价值函数。

• State-Value Function： 表示在状态 s 下的价值，即从状态 s 开始，按照某个策略 π 执行，最终获得的回报的期望值。 可以用来评估在状态 s 下的好坏，从而指导智能体的决策，即状态价值函数。

• Advantage Function：，表示在状态 s 下采取动作 a 相对于采取期望动作的优势。优势函数可以用来评估在状态 s 下采取动作 a 的优劣，从而指导智能体的决策，即优势函数。

有了这些概念，我们再回过头来看我们的目标梯度：

其中： 就是我们刚刚讲的优势函数，表示在状态 下采取动作 相对于采取期望动作的优势。去掉梯度符号，得到我们的目标函数：最大化优势函数的期望。

那如何计算优势函数呢？我们重新来看一下优势函数的定义：

表示在状态 s 下采取动作 a 的价值， 表示在状态 s 下的价值。我们来看一下下面这个公式：

其中：

• ：执行动作 a 后，在状态 下获得的即时奖励。

• ：折扣因子，用于确定未来奖励的重要性。折扣因子接近 1 时，更加关注未来的奖励；接近0时，更加重视即时奖励。

• ：价值函数，用参数 表示，估计下一个状态 的价值，即从该状态开始的预期未来奖励。

我们把上述公式代入到优势函数的定义中：

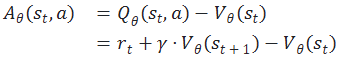
我们可以看到，现在优势函数中只剩下了状态价值函数 和下一个状态的价值函数 ，这样就由原来需要训练两个神经网络变成了只需要训练一个状态价值网络，这样就减少了训练的复杂度。

在上面的函数中，我们是对 Reward 进行一步采样，下面我们对状态价值函数也进行 action 和 reward 的一步采样。

接下里，我们就可以对优势函数进行多步采样，也可以全部采样。

从图片中提取的公式为：

我们知道，采样的步数越多，会导致方差越大，但偏差会越小。为了让式子更加简洁，定义：

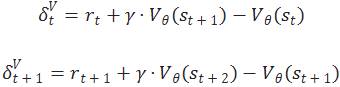
其中：

• ：是时间步 的优势函数，表示当前时刻 的即时奖励 加上下一个状态的折扣价值 减去当前状态的估计价值 .

那我们究竟要采样几步呢？介绍一下广义优势估计GAE (Generalized Advantage Estimation)，小孩子才做选择，我全都要。

将上面定义好的 和 代入到GAE优势函数中：

最终我们可以得到：

PPO

PPO (Proximal Policy Optimization) 邻近策略优化 是 OpenAI 提出的一种基于策略梯度的强化学习算法，它通过对策略梯度的优化，允许近期的旧数据 被多次用于梯度更新，减少与环境交互的次数，减少了重复采样的时间，让训练更快。PPO 算法的核心思想是在更新策略时，通过引入一个重要性采样比例，来限制策略更新的幅度，从而保证策略的稳定性。

首先了解一下重要性采样 (Importance Sampling)：其意义是从分布 q(x) 中采样 x 来求 f(x) 在 p(x) 分布下的期望。

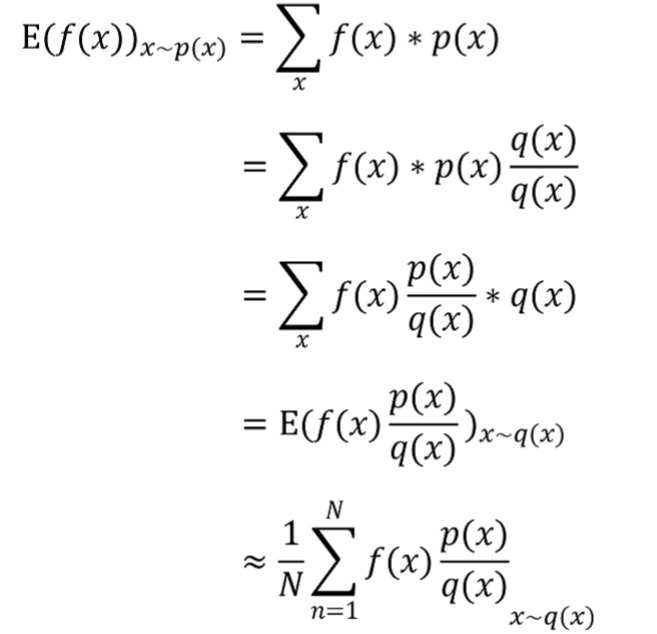
将其应用到前面的目标梯度中，得到 PPO 的目标梯度：

对应的损失函数为：

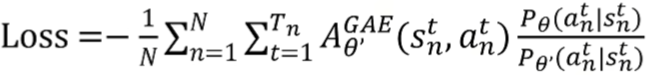
整个公式的作用是通过优势估计来计算策略梯度，以优化策略参数，使得策略倾向于选择优势更高的动作，从而提升策略性能。GAE 可以有效降低方差，使得策略优化过程更加稳定和高效。

PPO 根据不同的实现方法可以分为两类：

**PPO-Penalty：**用拉格朗日乘数法直接将 KL 散度的限制放进了目标函数中，并在迭代的过程中不断更新 KL 散度前的系数。即：

其中：

• ：是KL散度项，用于限制新旧策略之间的距离，其中 表示策略 和旧策略 之间的KL散度。超参数 控制 KL 散度项的权重，从而调节新旧策略之间的差异，防止策略更新过大导致不稳定。

整个 PPO-KL 损失函数的目的是通过限制新旧策略的差异（使用KL散度项）来优化策略，使其更稳定地朝着优势更高的方向进行更新。PPO 的这种约束策略更新的方法相比于其他策略优化方法更为稳定且有效。

**PPO-Clipped：**是 PPO 的另一种变体，又称为 PPO2，它通过对比新旧策略的比值，来限制策略更新的幅度，从而保证策略的稳定性。具体来说，PPO-Clipped 的目标函数为：

• ：裁剪函数，将概率比裁剪到 [1−ϵ,1+ϵ] 区间，防止策略的更新步长过大。这里 是一个超参数，控制裁剪的范围。

• ：在未裁剪的概率比项和裁剪后的项之间取最小值。这一操作的目的在于限制策略更新幅度，以防止策略偏离旧策略过远，从而导致不稳定的学习过程。

整个 PPO-clip 损失函数的作用是通过裁剪操作约束策略的变化幅度，使策略更新不会过于激进。这种方式相比于传统策略梯度方法更为稳定，并且在优化过程中能够有效平衡探索和利用。PPO2 的这种裁剪机制是其成功的关键，广泛用于实际的强化学习应用中。