TL;DR
- 场景:梳理分类决策树的结构、学习流程与"条件概率分布"解释,并给出香农熵代码实现。
- 结论:决策树可视为对分区区域上的 P(Y\mid X\in R_j) 建模;划分依据由不纯度度量(熵/基尼/误分类率)驱动,过拟合需靠剪枝控制。
- 产出:决策树节点/流程框架 + 概率解释链路 + 香农熵公式对照 + Pandas 代码可复用实现。

决策树模型
- 树模型是有监督学习类算法中应用广泛的一类模型,同时可应用与分类问题和回归问题,其中用于解决分类问题的树模型常被称为分类树,而用于解决回归类问题的树模型被称为回归树。
- 树模型通过递归式切割的方法来寻找最佳分类标准,进而最终形成规则。
- 其算法原理虽然简单,但模型本身使用面极广,且在分类问题和回归问题上均有良好的表现,外加使用简单,无需人为进行过多变量调整和数据预处理,同时生成规则清晰,模型本身可解释性非常强,因此在各个行业均有广泛应用。
- 决策树(Decision Tree)是一种实现分治策略的层次数据结构,它是一种有效的非参数学习方法,并可以用于分类和回归,我们主要讨论分类的决策树。
- 分类决策树模型表示一种基于特征对实例进行分类的属性结构(包括二叉树和多叉树)。
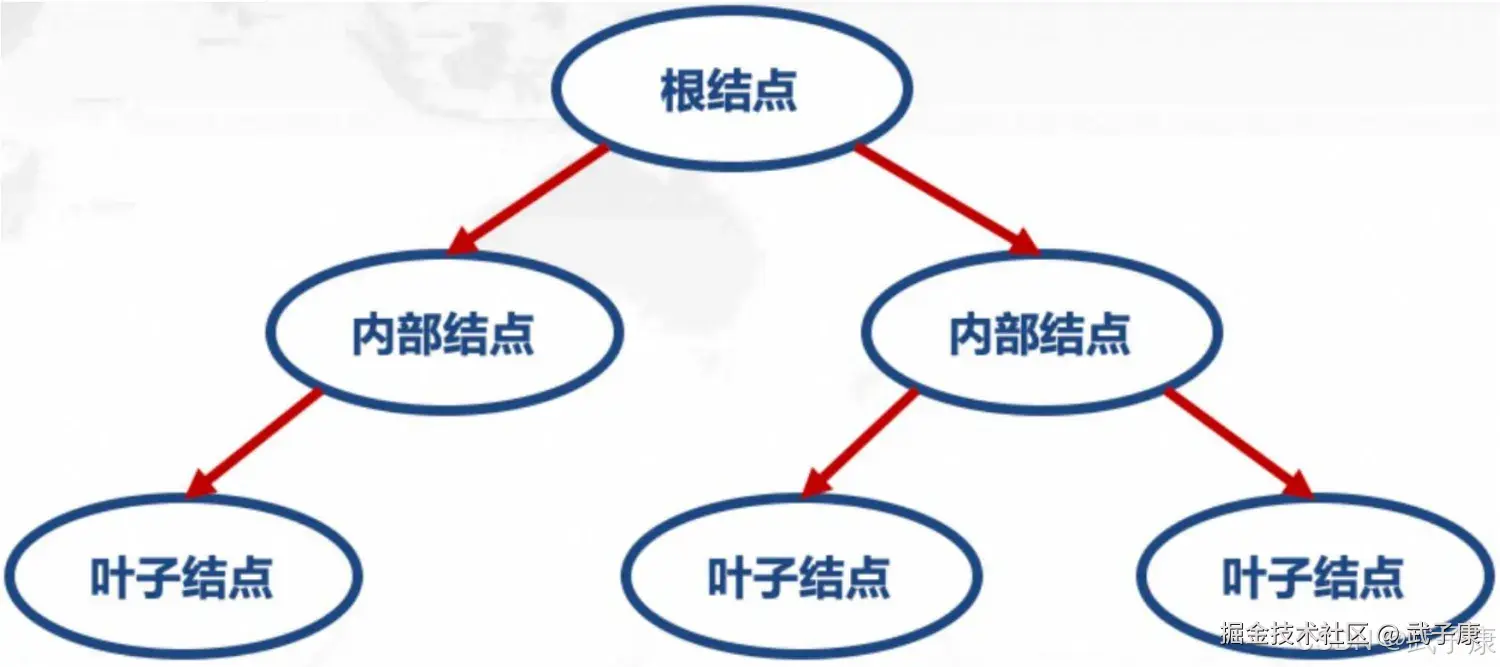
决策树由节点(Node)和有向边(Directed edge)组成,树中包含三种节点:
- 根节点(Root Node):包含样本全集,没有入边,但有零条或多条多边。
- 内部节点(Internal Node):对应于属性测试条件,恰有一条入边,和两条或多条出边。
- 叶节点(Leaf Node)或终节点(Terminal Node):对应于决策结果,恰有一条入边,但没有出边。
决策树基本流程
从根节点到每个叶子节点的路径对应了一个判定测试序列,其基本流程遵循了简单且直观的"分而治之"策略。 由此,局部区域通过少数几步递归分裂确定,每个决策节点实现一个具有离散输出的属性测试函数,标记分支。 假设给定训练集输入: 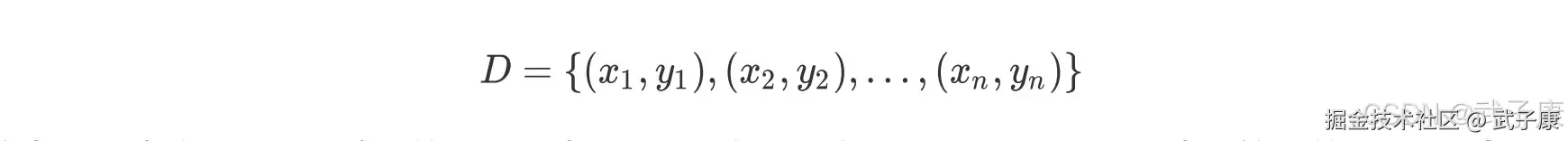 在每个节点应用一个测试,并根据测试的输出确定一个分支,这一过程从跟节点开始,并递归的重复,直至到达一个叶子节点,这是,该 leaf 的值形成输出。
在每个节点应用一个测试,并根据测试的输出确定一个分支,这一过程从跟节点开始,并递归的重复,直至到达一个叶子节点,这是,该 leaf 的值形成输出。
决策与条件概率分布
决策树是一种基于概率统计的机器学习模型,其本质可以理解为在给定决策节点下对类别变量的条件概率分布建模。具体来说:
- 概率分布的定义与划分:
- 决策树将特征空间 X 划分为若干个互不重叠的区域 R1, R2,..., Rm
- 在每个区域 Rj 上定义了一个条件概率分布 P(Y|X ∈ Rj)
- 这个概率分布定义在类别变量 Y 的所有可能取值上
- 树结构的概率解释:
- 根节点对应整个特征空间的初始划分
- 每个内部决策节点代表对当前区域的进一步细分
- 随着从根节点到叶节点的路径延伸,特征空间被递归地划分为更小的子区域
- 最终每个叶节点对应特征空间的一个特定区域 Rj
- 条件概率的特性:
- 在训练过程中,通过统计落入每个区域的样本类别分布来估计 P(Y|X ∈ Rj)
- 通常情况下,叶节点上的条件概率会呈现明显偏向性,即某个类别的概率显著高于其他类别
- 例如,在二分类问题中,某个叶节点可能得到 P(Y=1|X ∈ Rj)=0.85,P(Y=0|X ∈ Rj)=0.15
- 分类决策过程:
- 对于新样本 x,决策树会将其路由到对应的叶节点(区域 Rj)
- 根据该节点的条件概率分布,采用最大后验概率(MAP)准则进行分类: ŷ = argmax_y P(Y=y|X ∈ Rj)
- 这意味着即使某个类别的概率不是100%,决策树仍会将该样本强行划分到概率最大的类别
- 实际应用示例:
- 在信用评分模型中,决策树可能将"年收入>50万且负债率<30%"的区域分配给"低风险"类别,概率为92%
- 在医疗诊断中,某个叶节点可能表示"体温>38.5℃且白细胞计数>10^4"条件下,患细菌性肺炎的概率为78%
这种概率解释框架为理解决策树的工作原理提供了理论基础,也解释了为什么决策树容易在训练数据上达到100%准确率(通过不断细分直到每个叶节点只包含单一类别的样本)。
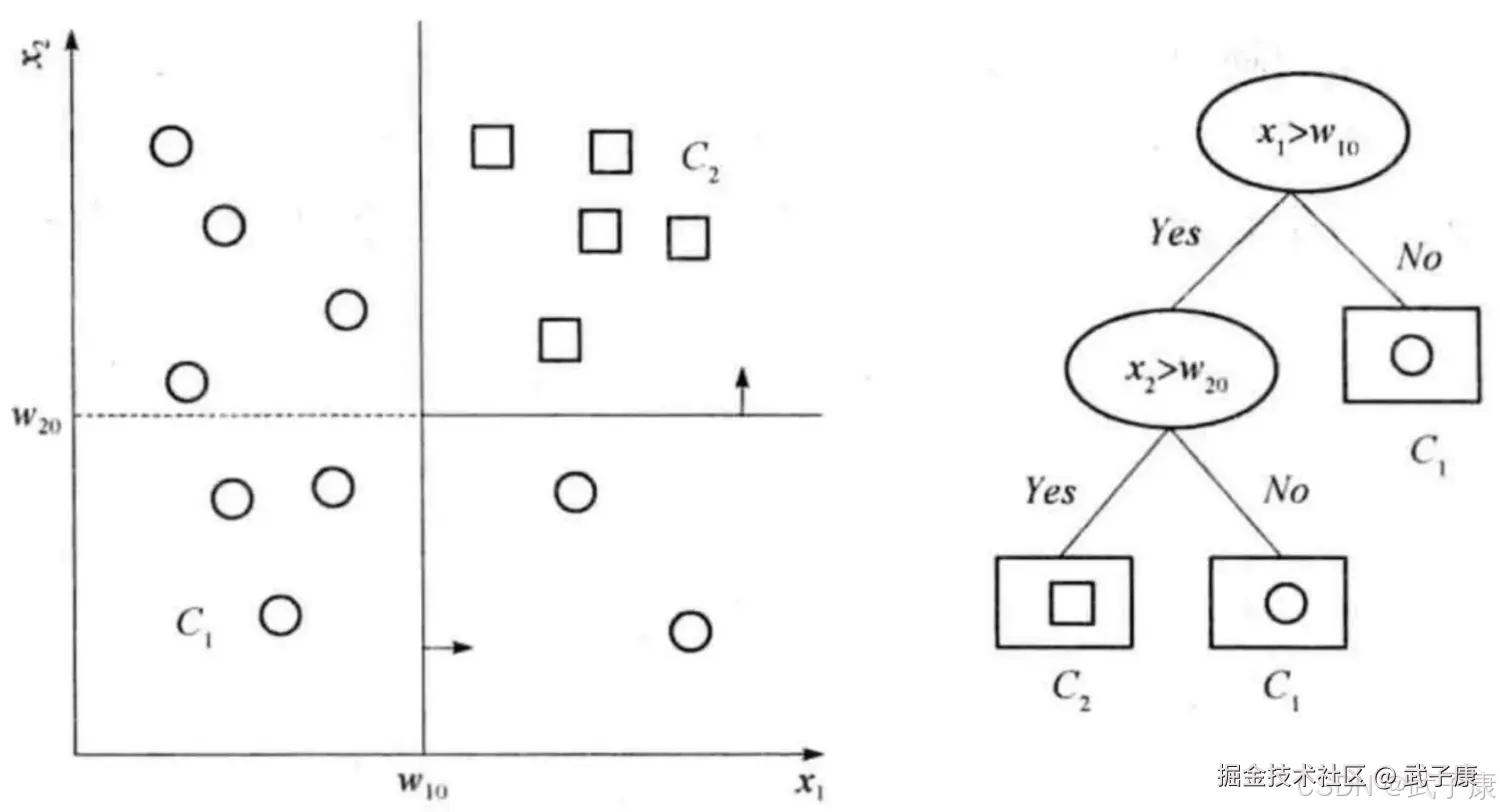 左图表示了特征空间的一个划分,假定现在只有 W10 和 W20 两个决策点,特征空间被决策点沿轴划分,并且相继划分相互正交,每个小矩形表示一个区域,特征空间上的区域构成了集合,X 取值为区域的集合。 我们在这里只假设两类,即 Y 的取值为 方块、圆圈。当某个区域 C 的条件概率分布满足 P(Y=圆圈|X=C)> 0.5 时,则认为这个区域属于圆圈类,即落在这个区域的实例都被视为该类。 右图为对应于概率分布的决策树,如果输入维是 Xn 是离散的,取 N 个可能的值之一,则该决策节点检查 Xn 的值,并取相应分支,实现一个 n 路划分。因此,如果决策节点具有离散分支,数值输入应当离散化。
左图表示了特征空间的一个划分,假定现在只有 W10 和 W20 两个决策点,特征空间被决策点沿轴划分,并且相继划分相互正交,每个小矩形表示一个区域,特征空间上的区域构成了集合,X 取值为区域的集合。 我们在这里只假设两类,即 Y 的取值为 方块、圆圈。当某个区域 C 的条件概率分布满足 P(Y=圆圈|X=C)> 0.5 时,则认为这个区域属于圆圈类,即落在这个区域的实例都被视为该类。 右图为对应于概率分布的决策树,如果输入维是 Xn 是离散的,取 N 个可能的值之一,则该决策节点检查 Xn 的值,并取相应分支,实现一个 n 路划分。因此,如果决策节点具有离散分支,数值输入应当离散化。

学习算法
决策树学习是一种通过归纳训练数据集来构建分类规则的机器学习方法,也称为"树归纳"过程。这一过程具有以下几个关键特征:
- 模型选择原则
- 对于同一个训练数据集,可能存在无数棵能够完美分类的决策树。我们追求的是其中"最小"的树,这里的"最小"通常通过两种方式衡量:
- 树的节点总数(包括内部节点和叶节点)
- 决策节点的复杂性(如划分条件的复杂程度)
- 从概率角度解释,决策树实际上是在估计条件概率模型。在特征空间划分下,存在无数个可能的条件概率模型,我们选择的标准是:
- 对训练数据具有良好的拟合度
- 同时具备良好的泛化能力(对未知数据的预测准确性)
- 算法执行过程
- 算法开始时,整个训练数据集位于根节点
- 在每个划分步骤中,算法会:
- 对于连续值属性:寻找最优分割点将数据划分为两个子集
- 对于离散值属性:根据属性值将数据划分为N个子集(N为属性取值个数)
- 划分标准通常基于:
- 信息增益(ID3算法)
- 信息增益比(C4.5算法)
- 基尼指数(CART算法)
- 递归地对每个子集重复上述过程,直到满足以下任一停止条件:
- 当前子集中的样本基本属于同一类别(如95%以上)
- 没有合适的特征可供继续划分
- 达到预设的树深度限制
- 当停止条件满足时,创建叶节点并标记为当前子集中的主要类别
- 典型应用场景
- 医疗诊断:根据患者症状判断疾病类型
- 信用评估:根据客户特征预测还款能力
- 工业生产:根据设备参数判断故障类型
示例:在鸢尾花分类问题中,决策树可能首先根据花瓣长度进行划分(如<2.45cm为一类),然后在每个子集中继续根据其他特征(如花瓣宽度、萼片长度等)进行细分,最终形成一棵能够准确分类三种鸢尾花的决策树。
注意:实际应用中通常会通过剪枝(pre-pruning或post-pruning)等技术来防止过拟合,提高模型的泛化能力。
综上,决策树学习算法包括特征选择、决策树的生成与决策树的剪枝。 由于决策树表示一个条件概率的分布,所以深浅不同的决策树对应着不同的复杂度的概率模型,其中决策树的生成只考虑局部最优,相对的,决策树的剪枝则考虑全局最优。
香农熵的计算
决策树学习的关键在如何选择最优划分属性,一般而言,随着划分过程不断进行,我们希望决策树的分支节点所包含的样本尽可能属于同一类别,即节点纯度(purity)越来越高。在分类树中,划分的优劣用不纯度度量(impurity-measure)定量分析。
 在信息论与概率统计中,熵是表示随机变量不确定性的度量。这里我们使用的熵,也叫做香农熵,这个名字来源信息论之父克劳德·香农。
在信息论与概率统计中,熵是表示随机变量不确定性的度量。这里我们使用的熵,也叫做香农熵,这个名字来源信息论之父克劳德·香农。
为了计算熵,我们需要计算所有类别所有可能值包含的信息期望值(数学期望),即上述公式。对于二分类问题,如果 p1=1 而 p2 = 0,则出油的实例都属于 Ci 类。 如果 p1 = p2 = 0.5,熵为 1。
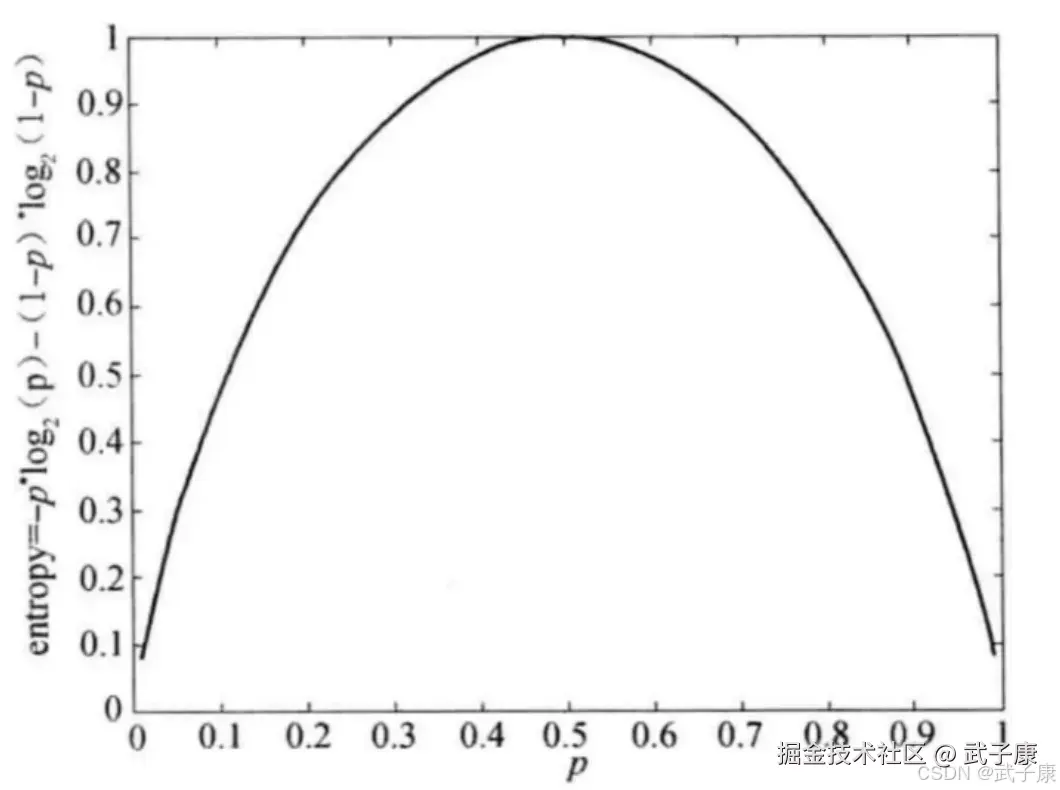 但是,熵并非是唯一可能的度量。
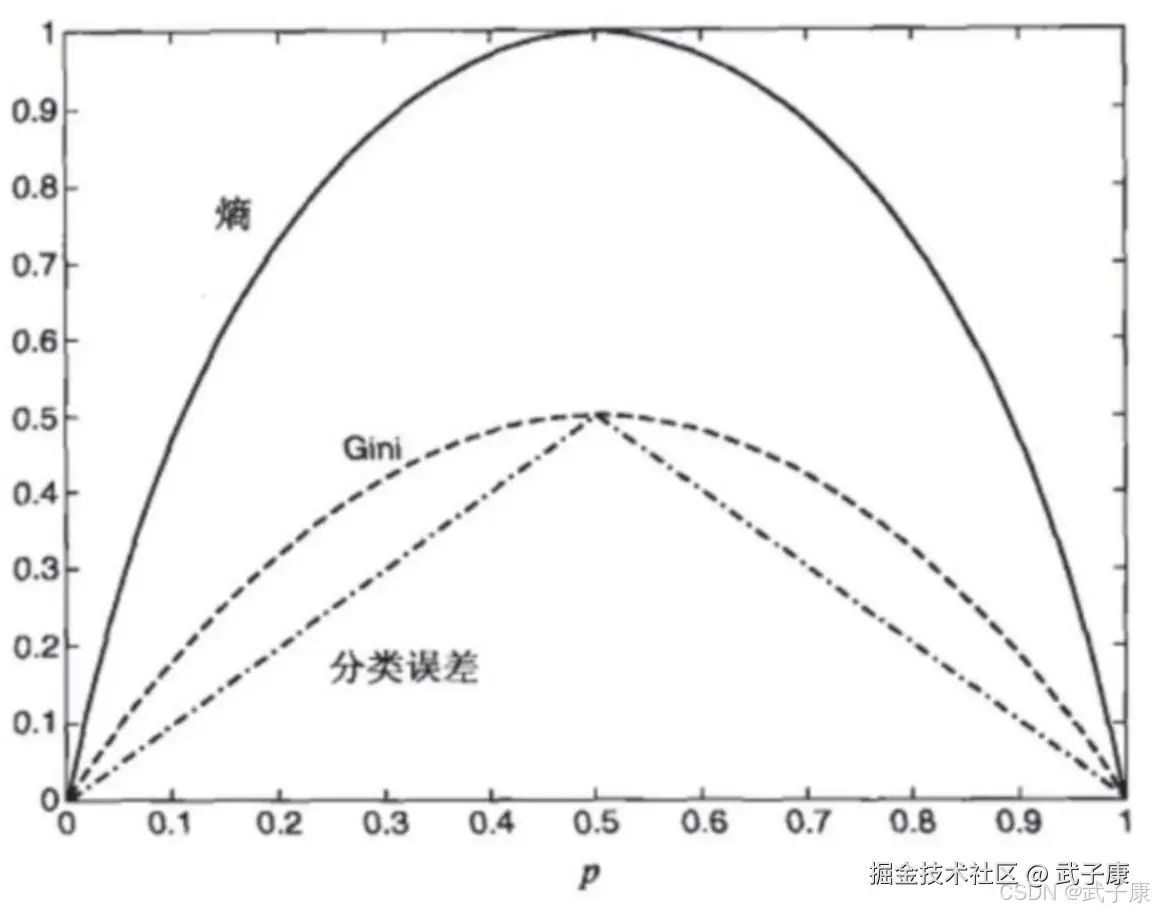
但是,熵并非是唯一可能的度量。  这些都可以推广到 K > 2 类,并且给定损失函数,误分类误差可以推广到最小风险。 下图显示了二元分类问题不纯性度量值的比较,p 表示属于其中一个类的记录所占的比例。从图中可以看出,三种方法都在类分布均衡时(即当 p=0.5 时)达到最大值,而当所有记录都属于同一个类时(p=1 或 p=0)达到最小值。
这些都可以推广到 K > 2 类,并且给定损失函数,误分类误差可以推广到最小风险。 下图显示了二元分类问题不纯性度量值的比较,p 表示属于其中一个类的记录所占的比例。从图中可以看出,三种方法都在类分布均衡时(即当 p=0.5 时)达到最大值,而当所有记录都属于同一个类时(p=1 或 p=0)达到最小值。
 这里给出三种不纯性度量方法的计算实例:
这里给出三种不纯性度量方法的计算实例:
 从上面的例子及图中可以看出,不同的不纯性度量是一致的。根据计算,节点 N1 具有最低的不纯性度量值,然后依次是 N2、N3。虽然结果是一致的,但是作为测试条件的属性选择仍然因不纯性度量的选择而异。
从上面的例子及图中可以看出,不同的不纯性度量是一致的。根据计算,节点 N1 具有最低的不纯性度量值,然后依次是 N2、N3。虽然结果是一致的,但是作为测试条件的属性选择仍然因不纯性度量的选择而异。
香农熵的代码实现
python
row_data = {
'是否陪伴' :[0,0,0,1,1],
'是否玩游戏':[1,1,0,1,1],
'渣男' :['是','是','不是','不是','不是']
}
dataSet = pd.DataFrame(row_data)
dataSet执行结果如下图所示: 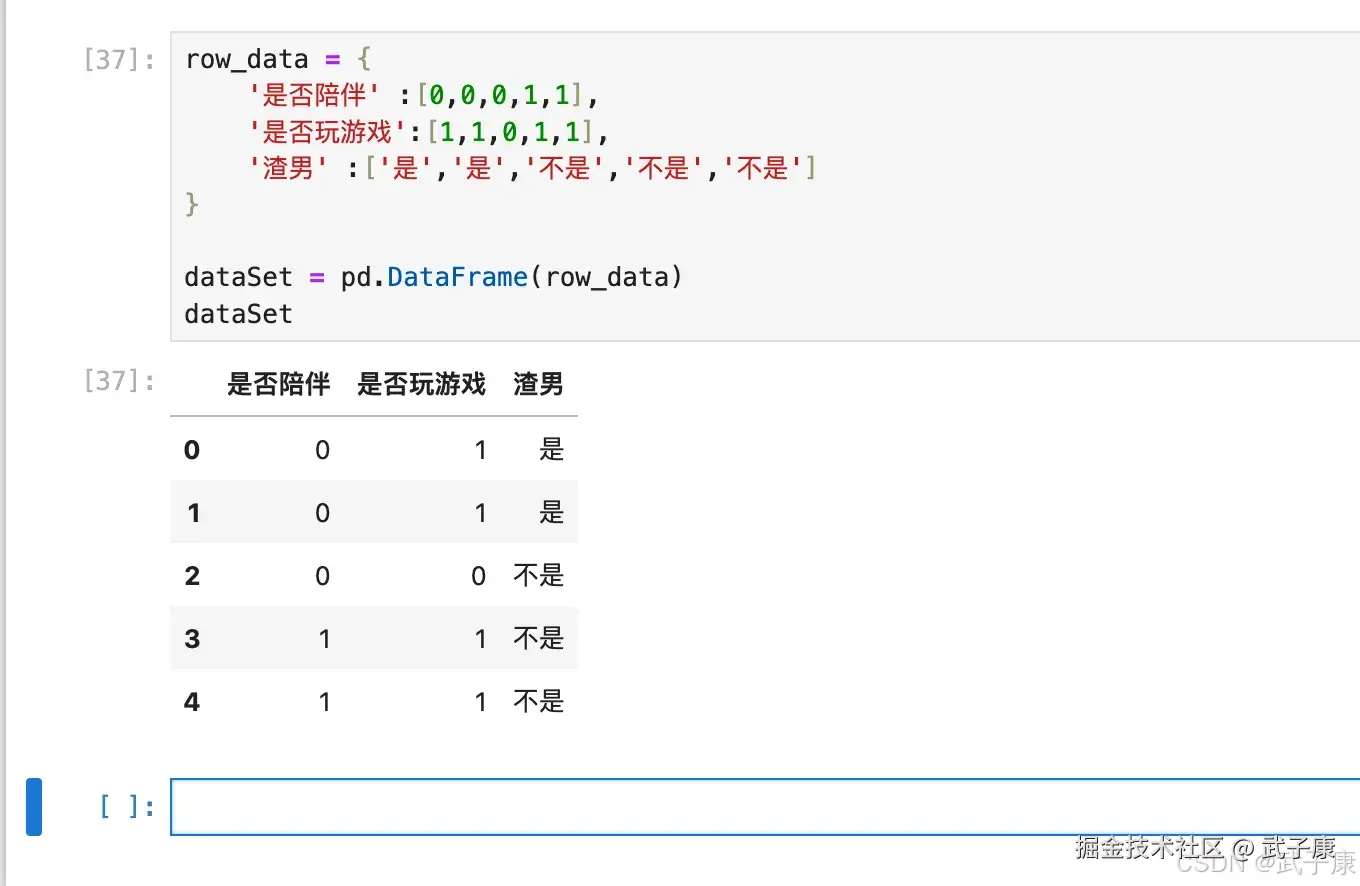 通过代码实现一下:
通过代码实现一下:
python
def calEnt(dataSet):
# 数据集总行数
n = dataSet.shape[0]
# 标签的所有类别
iset = dataSet.iloc[:,-1].value_counts()
# 每一类标签所占比
p = iset/n
# 计算信息熵
ent = (-p*np.log2(p)).sum()
return ent
calEnt(dataSet)运行的结果如下图所示: 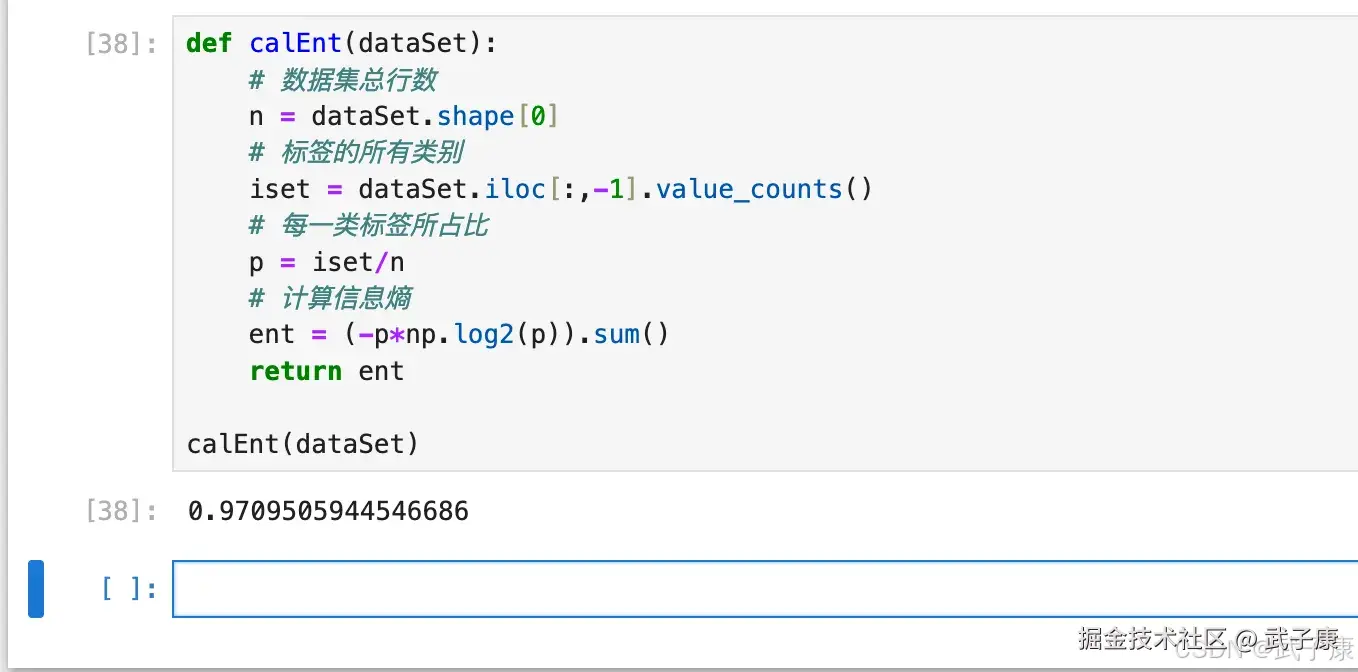 熵越高,信息的不纯度就越高,则混合的数据就越多。 也就是说,单从判断的结果来看,如果你从这 5 个人中瞎猜,要准确判断其中一个人是不是"bad boy"是不容易的。
熵越高,信息的不纯度就越高,则混合的数据就越多。 也就是说,单从判断的结果来看,如果你从这 5 个人中瞎猜,要准确判断其中一个人是不是"bad boy"是不容易的。
错误速查
| 症状 | 根因定位 | 修复 |
|---|---|---|
| 训练集准确率极高,测试集明显下降 | 树太深、叶子样本数过小,持续细分导致过拟合 | 看树深度、叶节点样本数分布、验证集曲线预剪枝(max_depth/min_samples_leaf/min_samples_split)、后剪枝(代价复杂度剪枝等) |
| 划分结果不稳定、轻微数据扰动树结构大变 | 决策树高方差模型,对采样/噪声敏感 | 多次不同随机种子训练对比树结构用集成方法(RandomForest/GBDT)或限制深度、增加叶子最小样本 |
| 连续特征划分效果差或解释困难 | 连续变量切分点选择不佳;或离散化策略不合理 | 检查候选切分点枚举/排序逻辑;观察分裂后纯度变化采用基于不纯度的最优切分点搜索;必要时做分箱并验证信息增益变化 |
| 类别极不均衡时,叶子节点概率偏置明显 | 叶节点 P(Y\mid X\in R_j) 被多数类主导 | 看叶节点类别计数与概率代价敏感学习/类权重/重采样;评估指标改用F1/PR-AUC |
| 熵计算得到 NaN/inf | 概率为0导致 \log(0) | 打印 value_counts 与 p;检查是否出现0概率项对概率加极小值 epsilon;或在计算中跳过 p=0 的项 |
| Pandas 代码报 NameError:pd/np 未定义 | 未导入库 | 查看执行环境 import补充 import pandas as pd、import numpy as np |
| value_counts() 结果顺序与预期不一致 | 默认按频次降序,不按标签顺序 | 打印 value_counts 输出明确排序需求:sort_index() 或指定类别顺序(Categorical) |
| 误把"熵越高=信息越多"当作"越好" | 熵表示不确定性/混杂度,训练中希望分裂后不纯度下降 | 对比分裂前后熵/基尼变化强调目标是降低不纯度(提升纯度),熵高通常表示更难分 |
| 认为"不同不纯度度量结果一致→属性选择一定一致" | 度量排序可能一致,但最佳划分属性可能不同 | 同一数据用熵/基尼分别算一次候选特征分数说明度量一致性不等价于选择一致;用交叉验证或业务约束选型 |
其他系列
🚀 AI篇持续更新中(长期更新)
AI炼丹日志-29 - 字节跳动 DeerFlow 深度研究框斜体样式架 私有部署 测试上手 架构研究 ,持续打造实用AI工具指南! AI研究-132 Java 生态前沿 2025:Spring、Quarkus、GraalVM、CRaC 与云原生落地
💻 Java篇持续更新中(长期更新)
Java-207 RabbitMQ Direct 交换器路由:RoutingKey 精确匹配、队列多绑定与日志分流实战 MyBatis 已完结,Spring 已完结,Nginx已完结,Tomcat已完结,分布式服务已完结,Dubbo已完结,MySQL已完结,MongoDB已完结,Neo4j已完结,FastDFS 已完结,OSS已完结,GuavaCache已完结,EVCache已完结,RabbitMQ正在更新... 深入浅出助你打牢基础!
📊 大数据板块已完成多项干货更新(300篇):
包括 Hadoop、Hive、Kafka、Flink、ClickHouse、Elasticsearch 等二十余项核心组件,覆盖离线+实时数仓全栈! 大数据-278 Spark MLib - 基础介绍 机器学习算法 梯度提升树 GBDT案例 详解