【论文笔记】DeepSeekMath-V2: 基于自我验证的数学推理新范式

文章目录

一、核心要点
二、研究背景
- [2.1 传统的数学推理强化学习方法的局限性](#2.1 传统的数学推理强化学习方法的局限性)
- [2.2 自我可验证是数学推理的关键一步](#2.2 自我可验证是数学推理的关键一步)
三、主要方法
- [3.1 总体框架概述](#3.1 总体框架概述)
- [3.2 Verifier：证明验证器](#3.2 Verifier：证明验证器)
- - [3.2.1 验证目标](#3.2.1 验证目标)
  - [3.2.2 Verifier 训练过程-RL](#3.2.2 Verifier 训练过程-RL)
- [3.3 Meta-Verifier: 验证分析的二级审查器](#3.3 Meta-Verifier: 验证分析的二级审查器)
- - [3.3.1 引入的原因与作用](#3.3.1 引入的原因与作用)
  - [3.3.2 Meta-Verifier 训练过程](#3.3.2 Meta-Verifier 训练过程)
  - [3.3.3 将元验证反馈整合进验证器训练](#3.3.3 将元验证反馈整合进验证器训练)
- [3.4 Generator：证明生成器](#3.4 Generator：证明生成器)
- - [3.4.1 优化目标的转变](#3.4.1 优化目标的转变)
  - [3.4.2 自我验证训练机制](#3.4.2 自我验证训练机制)
- [3.5 Verifier 与 Generator 的协同进化](#3.5 Verifier 与 Generator 的协同进化)
- - [3.5.1 自动化协同标注流程](#3.5.1 自动化协同标注流程)
  - [3.5.2 类 GAN 视角下的协同进化机制分析*](#3.5.2 类 GAN 视角下的协同进化机制分析*)
四、实验
- [4.1 训练设置](#4.1 训练设置)
- - [4.1.1 强化学习方法](#4.1.1 强化学习方法)
  - [4.1.2 训练顺序](#4.1.2 训练顺序)
  - [4.1.3 实验结果](#4.1.3 实验结果)
- [4.2 生成 → 自我分析 → 再生成](#4.2 生成 → 自我分析 → 再生成)
- [4.3 高计算量搜索](#4.3 高计算量搜索)
五、小结

原文摘要：大型语言模型在数学推理领域取得了显著进展，成为人工智能的重要测试平台，并可能对科学研究产生深远影响。通过强化学习奖励正确答案，这些模型在一年内从表现不佳提升到饱和了AIME和HMMT等定量推理竞赛的水平。然而，这种方法存在局限性：高准确率的最终答案无法保证推理过程的正确性，且对于需要严格推导的定理证明任务并不适用。为了突破这一限制，研究者提出通过自我验证来确保数学推理的全面性和严谨性，这对于解决开放性问题尤为重要。DeepSeekMath-V2通过训练一个基于大型语言模型的验证器来评估证明的正确性，并将其作为奖励模型训练证明生成器，激励其在最终确定证明前识别并解决问题。此外，通过扩展验证计算能力自动标记难以验证的证明，进一步优化验证器。该模型在IMO 2025和CMO 2024中获得金牌水平的分数，并在Putnam 2024中取得接近完美的成绩，证明了自我验证数学推理的可行性，为开发更强大的数学AI提供了新方向。

一、核心要点

DeepSeekMath-V2 提出了一种 面向自我验证的数学推理方法，突破了传统大语言模型仅关注最终答案正确性的问题。具体来说：

传统强化学习方法通过奖励最终答案提升性能，但无法保证推理链条的严谨性与完整性。
DeepSeekMath-V2 引入 Verifier（验证器）+ Generator（生成器）协同机制：生成器产生证明，验证器对推理步骤进行严格检查并反馈错误。
通过不断迭代验证与自我修正，该系统能生成既正确又逻辑完备的数学证明。
模型经过 scaled test-time compute（扩展测试时算力）后，在 IMO、CMO、Putnam 等高难度数学竞赛上表现出色。

二、研究背景

2.1 传统的数学推理强化学习方法的局限性

数学推理一直是 AI 推理能力的核心挑战。传统的数学推理强化学习方法通过对定量推理问题的最终答案是否与真实答案匹配来给予奖励，让LLM在主要评估最终答案的数学竞赛（如AIME和HMMT）中达到饱和水平。但这种奖励机制在数学证明类任务中存在两个根本性限制:

正确答案 ≠ 正确推理: 模型可能通过错误的逻辑得出正确答案。
不适用于定理证明任务: 数学证明需要严谨的逐步演绎。

这种 Final Answer Reward 训练范式造成的结果：

模型缺乏验证证明有效性的能力，表现出较高的假阳性率。
即使明显存在逻辑缺陷，也常常声称证明是正确的。

DeepSeekMath-V2 的出现就是为了解决这一根本性问题。

2.2 自我可验证是数学推理的关键一步

基于人类启发，对自我验证能力的三条关键观察：

无需参考解的错误发现能力：人类在数学证明中，即使没有标准答案，也能通过逻辑一致性和推理完整性发现潜在错误。这表明模型应具备独立评估自身推理正确性的能力，而无需依赖外部参考解。
多轮验证未发现错误意味着更高的可信度：如果一个证明在多次、多角度的验证后仍未暴露问题，其正确性的可信度显著提升。
错误识别难度可作为证明质量的代理指标：在人类推理中，发现错误的难度与证明质量相关。越严谨的证明越难被快速指出问题。因此，验证器对难以识别错误的证明赋予更高评分，驱动生成器优化推理结构，提升逻辑严谨性。

三、主要方法

3.1 总体框架概述

DeepSeekMath-V2 的核心目标是：训练一个不仅能给出正确答案，而且其推理过程本身"难以被否定"的数学推理模型 。为此提出了一套以 自我可验证（Self-Verification） 为核心的生成--验证协同框架。它由三个核心组件构成：

Generator（生成器）：负责生成完整的数学推理过程或证明；
Verifier（验证器）：负责评估生成推理中是否存在逻辑错误、不完整推导或不严谨步骤。
Meta-Verifier（元验证器）：用于对 Verifier 的证明分析本身进行二级评估。

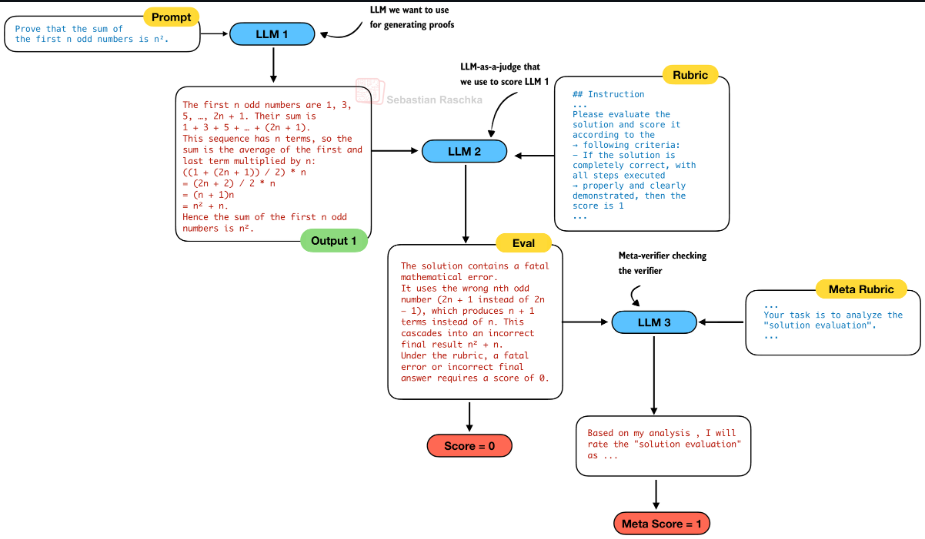
注：Generator (LLM 1)、Verifier (LLM 2)、Meta-Verifier (LLM 3)

通过这三个组件，生成--验证形成一个完整的闭环系统：Generator 生成证明 → Verifier 尝试发现问题并评分（Meta-Verifier 约束验证质量） → 奖励信号反向优化 Generator。

3.2 Verifier：证明验证器

3.2.1 验证目标

Verifier 的目标并非判断"答案是否正确"，而是回答：该推理过程中是否存在可被明确指出的错误？

给定一个问题 X X X 和一个证明 Y Y Y，验证器 π φ ( ⋅ ∣ X , Y , I ν ) \pi_{\varphi}(\cdot|X,Y,\mathcal{I}{\nu}) πφ(⋅∣X,Y,Iν) ( I ν I{\nu} Iν表示评分标准)生成一个证明分析，首先总结识别出的问题（如果有的话），然后根据三个等级给出评分：

对于完整且严谨的证明，所有逻辑步骤都清晰有理，评分为1
对于总体逻辑合理但存在小错误或遗漏细节的证明，评分为0.5
对于存在致命逻辑错误或关键漏洞的证明，评分为0。

此处，评分并不代表"证明一定正确"，而是"在当前验证能力下难以被否定"。

通过 Prompt引导 完成这项任务：

markdown 复制代码

## Instructions
Your task is to evaluate ...

Please evaluate the solution and score it according to the following criteria:
// 评分准则I_v

**Here is my evaluation of the solution:**
...// 评估分析

**Based on my evaluation, the final overall score should be:**
**\boxed{{...}}** // 最终打分结果 (0, 0.5, or 1, and nothing else)

---
Here is your task input:

## Problem
{question}

## Solution
{proof}

3.2.2 Verifier 训练过程-RL

初始强化学习数据集构建流程：

问题采集：从 Art of Problem Solving（AoPS）竞赛中爬取问题，共计 17,503 个问题（只选"必须写证明"的题）。
候选证明生成：使用 DeepSeek-V3.2-Exp-Thinking 的一个变体生成候选证明。（系统性地产生大量"思路合理但存在瑕疵"的真实证明样本）
人工评分：由数学专家根据评分标准给出整体评分(1/0.5/0),

由此得到初始强化学习数据集：

D ν = { ( X i , Y i , s i ) } , \mathcal{D}_{\nu} = \left\{ (X_i, Y_i, s_i) \right\}, Dν={(Xi,Yi,si)},

其中每个项目包括问题 X i X_i Xi、证明 Y i Y_i Yi 和总体评分 s i ∈ { 0 , 0.5 , 1 } s_i \in \{0, 0.5, 1\} si∈{0,0.5,1}。

强化学习目标:

基于经过监督微调的 DeepSeek-V3.2-Exp-SFT 训练验证器, 使用两个奖励组件：

格式奖励 R f o r m a t R_{\mathrm{format}} Rformat ：指示函数，确保输出包含关键短语
- "Here is my evaluation of the solution:"
- "Based on my evaluation, the final overall score should be:"
  并在之后给出评分 \boxed{}。
评分奖励 R s c o r e R_{\mathrm{score}} Rscore ：衡量预测评分 s i ′ s'i si′ 与标注评分 s i s_i si 的接近程度：
R s c o r e ( s i ′ , s i ) = 1 − ∣ s i ′ − s i ∣ R{\mathrm{score}}(s'_i, s_i) = 1 - |s'_i - s_i| Rscore(si′,si)=1−∣si′−si∣

最终验证器的强化学习目标为：

max ⁡ π φ E ( X i , Y i , s i ) ∼ D ν , ( V i ′ , s i ′ ) ∼ π φ ( ⋅ ∣ X i , Y i ) [ R f o r m a t ( V i ′ ) ⋅ R s c o r e ( s i ′ , s i ) ] \operatorname*{max}{\pi{\varphi}} \mathbb{E}{(X_i, Y_i, s_i) \sim \mathcal{D}{\nu}, (V'i, s'i) \sim \pi{\varphi}(\cdot|X_i, Y_i)} \left[ R{\mathrm{format}}(V'i) \cdot R{\mathrm{score}}(s'_i, s_i) \right] πφmaxE(Xi,Yi,si)∼Dν,(Vi′,si′)∼πφ(⋅∣Xi,Yi)[Rformat(Vi′)⋅Rscore(si′,si)]

其中 V i ′ V'_i Vi′ 表示验证器的最终输出， s i ′ s'_i si′ 为从中提取的证明评分。

3.3 Meta-Verifier: 验证分析的二级审查器

3.3.1 引入的原因与作用

引入 Meta-Verifier 的原因：

Verifier能编出一套"看起来合理"的批评理由，并且分数预测正确，能拿满 reward，从而导致reward hacking。

Meta-Verifier 用于判断：

Verifier指出的问题是否真实存在；
所指出的问题是否能够合理支持其给出的证明评分；
分析过程是否符合评分标准 I ν \mathcal{I}_{\nu} Iν 的逻辑要求。

这个步骤也是通过prompt引导来完成的。

3.3.2 Meta-Verifier 训练过程

与Verifier训练方式类似，先获得一个初始验证器 π φ \pi_{\varphi} πφ。然后数学专家依据元验证标准 I m ν \mathcal{I}{m\nu} Imν，对Verifier生成的证明分析（ V i V_i Vi）的质量进行评分（ m s i ∈ { 0 , 0.5 , 1 } ms_i \in \{0, 0.5, 1\} msi∈{0,0.5,1}），构建元验证数据集： D m ν = { ( X i , Y i , V i , m s i ) } \mathcal{D}{m\nu} = \{(X_i, Y_i, V_i, ms_i)\} Dmν={(Xi,Yi,Vi,msi)}。

最后训练一个用于分析Verifier的证明分析元验证器 π η ( ⋅ ∣ X , Y , V , I m ν ) \pi_{\eta}(\cdot|X, Y, V, \mathcal{I}_{m\nu}) πη(⋅∣X,Y,V,Imν)

Meta-Verifier 的强化学习目标在结构上与 Verifier 相同，同样由格式奖励和评分奖励组成。

3.3.3 将元验证反馈整合进验证器训练

训练完成 Meta-Verifier 后，将其反馈引入 Verifier 的训练过程，将 Verifier 训练时的奖励函数扩展为：

R V = R f o r m a t ⋅ R s c o r e ⋅ R m e t a R_{V} = R_{\mathrm{format}} \cdot R_{\mathrm{score}} \cdot R_{\mathrm{meta}} RV=Rformat⋅Rscore⋅Rmeta

其中：

R f o r m a t R_{\mathrm{format}} Rformat 约束输出格式；
R s c o r e R_{\mathrm{score}} Rscore 衡量预测评分与专家评分的一致性；
R m e t a R_{\mathrm{meta}} Rmeta 为 Meta-Verifier 给出的分析质量评分。

使用该复合奖励函数训练后，Verifier 的证明分析平均质量评分（由 Meta-Verifier 评估）从 0.85 提升至 0.96；同时保持了证明评分预测的相同准确率。

Meta-Verifier 通过约束"分析本身的真实性"，从根本上缓解了 reward hacking 问题。

3.4 Generator：证明生成器

3.4.1 优化目标的转变

传统数学推理模型的训练目标通常是：最大化最终答案正确率。而此处的 Generator 的优化目标被重定义为最大化 Verifier 给予的验证评分:

max ⁡ π θ E X i ∼ D p , Y i ∼ π θ ( ⋅ ∣ X i ) [ R Y ] \operatorname*{max}{\pi{\theta}} \mathbb{E}{X{i} \sim \mathcal{D}{p}, Y{i} \sim \pi_{\theta}(\cdot|X_{i})} [R_{Y}] πθmaxEXi∼Dp,Yi∼πθ(⋅∣Xi)[RY]

其中 R Y R_{Y} RY 是由 π φ ( ⋅ ∣ X i , Y i , I ν ) \pi_{\varphi}(\cdot|X_{i}, Y_{i}, \mathcal{I}_{\nu}) πφ(⋅∣Xi,Yi,Iν) 产生的证明评分。

这意味着 Generator 会逐步学习生成更完整、更严谨、且更难被否定的证明，而非仅仅追求结论正确。

3.4.2 自我验证训练机制

对于 IMO、CMO 等高难度竞赛问题，生成器往往难以一次性生成完全正确的证明。但是当生成器被提示对自己的证明进行分析时，它倾向于过度自信 ，即使外部验证器能够轻易发现明显缺陷。这表明生成器本身并不具备严格的自我验证能力。

因此，在训练过程中显式引入自我验证任务 ，生成器 π θ \pi_{\theta} πθ 被 Prompt 引导 完成两个连续任务：

生成一个证明 Y Y Y；
对该证明进行自我分析 Z Z Z，其格式与评分标准 I ν \mathcal{I}_{\nu} Iν 与验证器完全一致。（自我分析中给出的预测证明评分记为 s ′ s' s′）

markdown 复制代码

...
## Solution
// 最终解答

## Self Evaluation
Here is my evaluation of the solution:
// 对解答的详细分析和自我评估

Based on my evaluation, the final overall score should be: \boxed{...}

---
Here is your task input:

## Problem
{quesiton}

为确保自我评估的可靠性，使用外部验证器 π φ \pi_{\varphi} πφ 对两个部分分别进行评估：

证明 Y Y Y 获得评分 R Y = s R_Y = s RY=s；
自我分析 Z Z Z 获得元验证评分 R m e t a ( Z ) = m s R_{\mathrm{meta}}(Z) = ms Rmeta(Z)=ms。

最终的强化学习奖励函数定义为：

R = R f o r m a t ( Y , Z ) ⋅ ( α ⋅ R Y + β ⋅ R Z ) R Z = R s c o r e ( s ′ , s ) ⋅ R m e t a ( Z ) \begin{aligned} R &= R_{\mathrm{format}}(Y, Z) \cdot (\alpha \cdot R_Y + \beta \cdot R_Z) \\ R_Z &= R_{\mathrm{score}}(s', s) \cdot R_{\mathrm{meta}}(Z) \end{aligned} RRZ=Rformat(Y,Z)⋅(α⋅RY+β⋅RZ)=Rscore(s′,s)⋅Rmeta(Z)

其中：

R s c o r e ( s ′ , s ) R_{\mathrm{score}}(s', s) Rscore(s′,s) 奖励自我评分与外部验证评分的一致性；
权重系数设置为 α = 0.76 \alpha = 0.76 α=0.76， β = 0.24 \beta = 0.24 β=0.24。

该奖励结构在训练中形成了明确的激励机制：

如实承认错误 比虚假宣称正确性获得更高奖励；
最高奖励来自于 生成正确证明并准确判断其严谨性；
对生成器而言，在最终输出前主动发现并修复问题是一种更优策略。

3.5 Verifier 与 Generator 的协同进化

验证器与生成器并非独立优化，而是形成一个持续演化的闭环系统：

验证器为生成器提供高质量、结构化的训练信号；
随着生成器能力提升，其生成的证明不断逼近验证器当前能力边界，从而反过来推动验证器进化。

这些"困难样本"（即在一次验证中未被成功否定的证明）构成了后续提升验证能力的关键训练数据来源。

3.5.1 自动化协同标注流程

对每个证明生成 n n n 个独立的验证器分析；
对评分为 0 或 0.5 的分析，生成 m m m 个元验证评估，若多数确认问题真实存在，则该分析被视为有效；
对每个证明：
- 若至少有 k k k 个有效分析给出最低评分，则证明被标记为该评分；
- 若所有验证尝试均未发现合法问题，则标记为 1；
- 否则证明被丢弃或交由专家审查。

在最后两轮训练迭代中，该流程完全取代人工标注，且自动标签与专家判断保持高度一致。

3.5.2 类 GAN 视角下的协同进化机制分析*

从机制角度看，Verifier--Generator 的协同进化过程在结构上与生成对抗网络（GAN）存在一定相似性，但二者在优化目标与训练稳定性设计上具有本质差异。

GAN 与 DeepSeekMath-V2 的对应关系

维度	GAN	DeepSeekMath-V2
生成组件	Generator	Proof Generator
判别组件	Discriminator	Proof Verifier
判别目标	区分真实 / 生成样本	识别证明中的逻辑问题
生成目标	欺骗判别器	生成"难以被否定"的证明
学习驱动力	判别失败样本	验证失败（困难）证明

在两者中，系统能力的提升均由"当前模型无法处理的样本"所驱动。

GAN 与 DeepSeekMath-V2 的核心差异

对比维度	GAN	DeepSeekMath-V2
博弈关系	严格零和	非零和、协同演化
失败的含义	判别器失败即系统失败	验证失败 = 新的高价值训练信号
稳定性机制	依赖技巧（正则、谱归一化等）	显式引入 Meta-Verifier
对抗对象	数据分布	推理与验证能力边界
优化目标	分布匹配	推理"不可反驳性"最大化

其中，Meta-Verifier 的引入尤为重要，它为验证器的分析质量提供了额外约束，用于评估其所指出问题的真实性与合理性，从而降低验证器通过生成表面合理但实际无效的批评来获得奖励的风险，避免训练过程中的 reward hacking 现象。

从这一视角看，DeepSeekMath-V2 的协同进化机制并非简单的对抗学习，而更接近一种以验证能力为约束、以困难样本为驱动的渐进式自举（bootstrapping）推理能力扩展机制。这种设计使系统能够在极少人工标注参与的情况下，持续提升推理严谨性，并实现从"答案正确"向"推理可信"的范式转变。

四、实验

4.1 训练设置

4.1.1 强化学习方法

使用 GRPO 算法作为统一的强化学习方法，训练 Verifier、Generator、Meta-Verifier，只是Reward不同。（GRPO 非常适合评分型的奖励（0/0.5/1））

4.1.2 训练顺序

"In each iteration, we first optimized proof verification."

每一轮训练顺序是单向的、固定的： 先 Verifier，后 Generator（用验证能力指导生成）

"The proof generator was then initialized from the verifier checkpoint"

Generator 不是独立模型，而是用已具备验证能力的 Verifier 权重作为初始化。

"Starting from the second iteration, the proof verifier was initialized with a checkpoint that consolidated both verification and generation capabilities from the previous iteration through rejection fine-tuning."

第二轮迭代开始：Verifier 也继承 Generator 的能力 ，这个融合通过 Rejection Fine-Tuning (RFT) 完成。

本质：Generator 与 Verifier 的参数初始化是共享/继承的，而不是长期对抗的。

大致流程图如下：
Rejection Fine-Tuning
Base LLM
Train Verifier (GRPO)
Verifier Checkpoint
Initialize Generator
Train Generator

(Self-Verification RL)
Consolidated Model

(Verifier + Generator)

4.1.3 实验结果

使用训练出的 Verifier 打分如图：

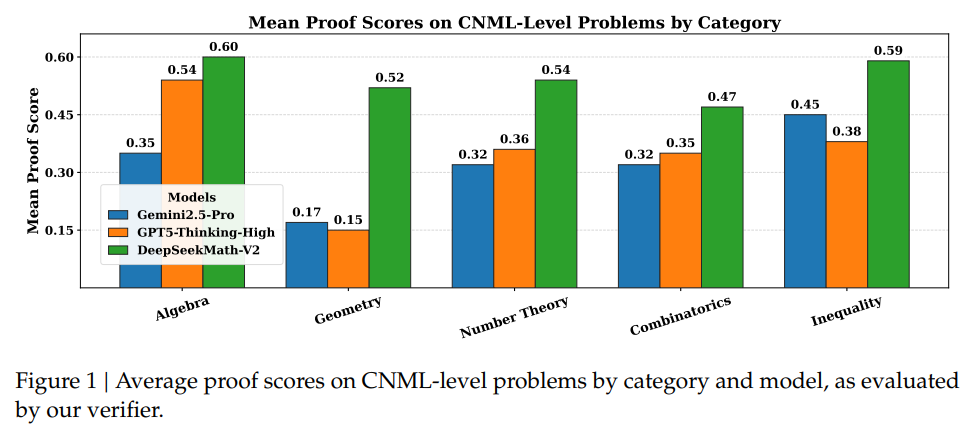
4.2 生成 → 自我分析 → 再生成

对于 IMO、CMO 这类高难度竞赛题 ，模型往往难以在单次生成（128K token 限制） 内给出完整、严谨的证明。

This approach first generates a proof with self-analysis, then iteratively re-prompts the generator with its previous output.

通过 "生成 → 自我分析 → 再生成" 的循环精炼机制，可以提高证明质量：

初始生成 ：Generator 先生成一个完整证明，并同时给出自我分析 / 自我评分。若模型在自我验证中判断证明不完美，则显式指出存在的问题。
精炼再提示 ：将上一轮证明 + 自我指出的问题作为新的上下文，再次提示生成器进行修正。
多轮迭代：重复上述过程，直到自评分达到满分或达到最大精炼轮数（8次）

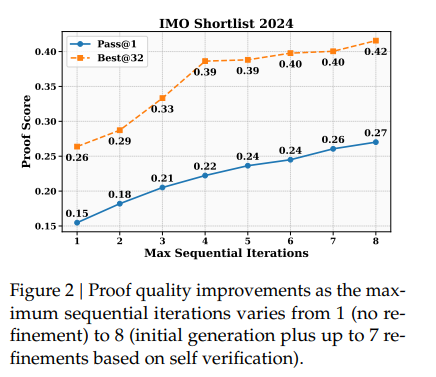
4.3 高计算量搜索

尽管序列精炼显著提升了证明质量，但对于最难的问题：

错误可能极其隐蔽
单条生成路径仍容易陷入局部最优
需要更大范围的策略探索 + 严格验证

因此，论文进一步引入 大规模并行搜索 + 高强度验证：

候选池初始化：64 个候选证明，每个候选对应 64 次独立验证
迭代修正：
- 根据平均验证分数，选出 得分最高的 64 个证明
- 将每个候选证明与 8 个随机选取的验证分析配对（优先验证分数低的）
- 每个证明-分析对生成一个改进的证明，随后更新候选池。
- 终止条件 ：（1）某个证明 通过全部 64 次验证（具有极高置信度）（2）达到最大迭代次数（16次）

整个过程中生成与验证使用同一个最终模型，即最终的 Generator。

五、小结

DeepSeekMath-V2 提出了一种以自我可验证（Self-Verification） 为核心的数学推理训练范式，突破了仅依赖最终答案正确性的传统奖励机制。该方法通过显式训练模型识别并修正自身推理中的潜在问题，使优化目标从"给出正确答案"转向"生成难以被否定的严谨推理过程"。

在方法层面，论文构建了一个由 证明生成器（Generator）---证明验证器（Verifier）---元验证器（Meta-Verifier） 组成的协同系统，并通过迭代式训练形成稳定的闭环。元验证机制在其中起到了关键约束作用，有效缓解了验证器的幻觉问题和 reward hacking 风险，从而保证了训练过程的可靠性。

该工作的重要技术贡献可以概括为四点：

构建了一个具备较高可靠性的、基于大语言模型的数学证明验证器；
通过元验证机制显式约束验证分析质量，显著降低幻觉问题；
将自我验证纳入生成器的训练目标，引导模型主动发现并修复推理缺陷；
通过扩展验证计算与自动化标注流程，减少对人工专家标注的依赖，实现验证能力的持续提升。