目录
GLM相关资料
https://glm.g-truc.net/0.9.9/api/modules.html
https://registry.khronos.org/OpenGL/specs/gl/GLSLangSpec.4.20.pdf
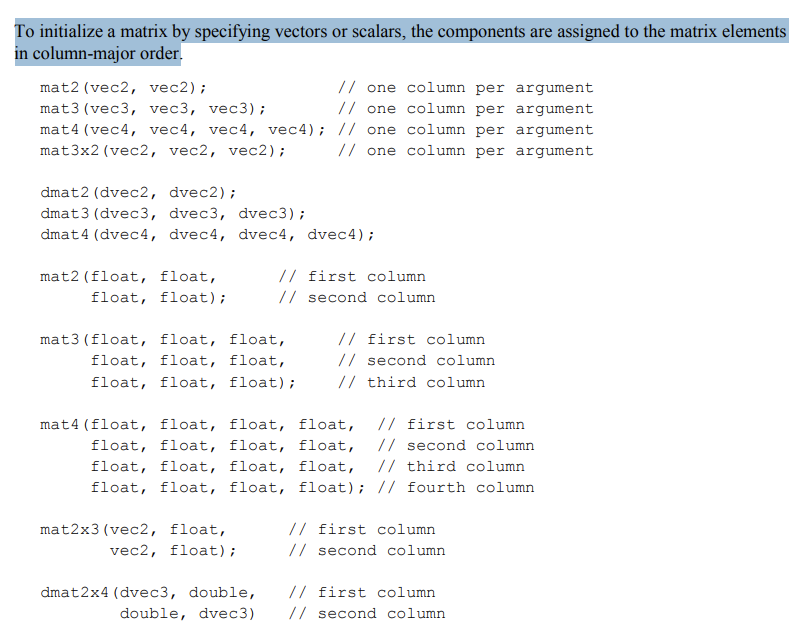
通过指定向量或标量来初始化矩阵时,各分量会按**列优先(column-major)**的顺序分配给矩阵元素。
Eigen相关资料
https://libeigen.gitlab.io/eigen/docs-3.3/
https://libeigen.gitlab.io/eigen/docs-nightly/group__TutorialAdvancedInitialization.html
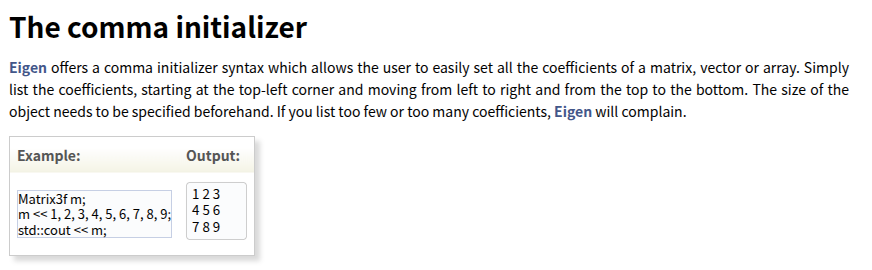
Eigen 提供了一种逗号初始化器语法,使用户能够轻松设置矩阵、向量或数组的所有系数。只需列出系数,从左上角开始,从左到右、从上到下依次排列。
https://libeigen.gitlab.io/eigen/docs-nightly/group__TopicStorageOrders.html
Eigen说明了行优先和列优化的两种存储方式,并且说明Matrix默认是列优先存储

测试验证
cpp
#include <glm/glm.hpp>
#include <Eigen/Core>
#include <iomanip>
void print_matrix(const std::string& name, const float* data, int rows, int cols) {
std::cout << name << " 内存布局:" << std::endl;
for (int i = 0; i < rows * cols; i++) {
std::cout << std::setw(6) << data[i] << " ";
if ((i + 1) % cols == 0) std::cout << std::endl;
}
std::cout << std::endl;
}
int main() {
// GLM测试
glm::mat3 glm_mat(1,2,3,4,5,6,7,8,9);
glm::vec3 glm_vec(1,0,0);
glm::vec3 glm_result = glm_mat * glm_vec;
std::cout <<"glm::mat3 glm_mat(1,2,3,4,5,6,7,8,9)\n";
std::cout << "GLM 矩阵 * [1,0,0]^T = ["
<< glm_result.x << ", " << glm_result.y << ", " << glm_result.z << "]"
<< " → 第一列" << std::endl;
const float* glm_data = &glm_mat[0][0];
print_matrix("glm_mat", glm_data, 3, 3);
glm::mat3 glm_mul = glm::transpose(glm_mat)*glm::transpose(glm_mat);
print_matrix("glm_mul", &glm_mul[0][0], 3, 3);
// Eigen测试
Eigen::Matrix3f eigen_mat;
eigen_mat << 1,2,3,4,5,6,7,8,9;
std::cout <<"Eigen::Matrix3f eigen_mat\neigen_mat << 1,2,3,4,5,6,7,8,9\n";
Eigen::Vector3f eigen_vec(1,0,0);
Eigen::Vector3f eigen_result = eigen_mat * eigen_vec;
std::cout << "Eigen 矩阵 * [1,0,0]^T = ["
<< eigen_result.transpose() << "]"
<< " → 第一列" << std::endl;
const float* eigen_data_ptr = eigen_mat.data();
print_matrix("eigen_mat", eigen_data_ptr, 3, 3);
std::cout << "Is row-major (via Flags)? " << ((eigen_mat.Flags & Eigen::RowMajorBit) != 0) << std::endl;
Eigen::Matrix3f eigen_mul = eigen_mat*eigen_mat;
print_matrix("eigen_mul", eigen_mul.data(), 3, 3);
{
Eigen::Matrix<float, 3, 3, Eigen::RowMajor> eigen_mat;
eigen_mat << 1,2,3,4,5,6,7,8,9;
std::cout <<"Eigen::Matrix<float, 3, 3, Eigen::RowMajor> eigen_mat\neigen_mat << 1,2,3,4,5,6,7,8,9\n";
Eigen::Vector3f eigen_vec(1,0,0);
Eigen::Vector3f eigen_result = eigen_mat * eigen_vec;
std::cout << "Eigen 矩阵 * [1,0,0]^T = ["
<< eigen_result.transpose() << "]"
<< " → 第一列" << std::endl;
const float* eigen_data_ptr = eigen_mat.data();
print_matrix("eigen_mat", eigen_data_ptr, 3, 3);
std::cout << "Is row-major (via Flags)? " << ((eigen_mat.Flags & Eigen::RowMajorBit) != 0) << std::endl;
Eigen::Matrix<float, 3, 3, Eigen::RowMajor> eigen_mul = eigen_mat*eigen_mat;
print_matrix("eigen_mul", eigen_mul.data(), 3, 3);
}
return 0;
}输出结果:
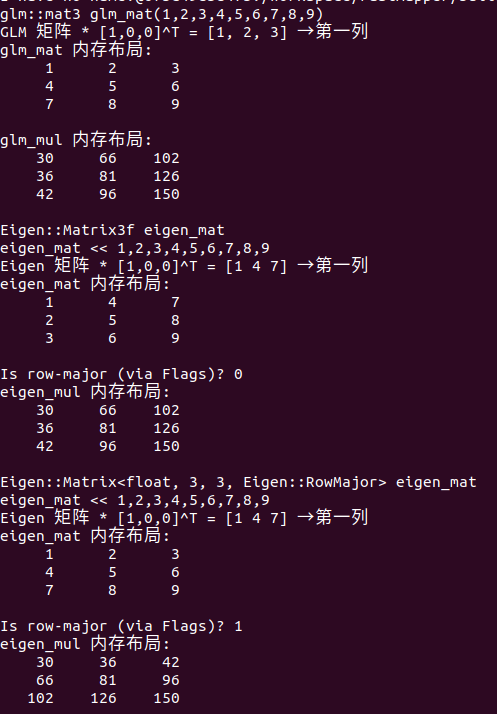
初始化方式的差异:1)GLM矩阵初始化是按照列优先分配;2)Eigen通过逗号初始化是行优先分配
存储差异:1)GLM矩阵只有列优先存储的方式;2)Eigen默认是列优先存储,并且提供参数可以用于指定不同存储方式,比如Eigen::RowMajor和Eigen::ColMajor
因此,同样的数据输入,比如说"1,2,3,4,5,6,7,8,9",
对于glm::mat3来说,实际上是定义了矩阵如下所示:
对于Eigen::Matrix3f或者Eigen::Matrix<float, 3, 3, Eigen::RowMajor>来说,实际上是定义了矩阵如下所示,
因此,同样的数据输入,glm::mat3矩阵需要进行装置才等价于Eigen::Matrix3f矩阵