概述
扩散模型的作用是将图片库喂给模型训练后可以随机生成一些与图片库中类似的图片。
训练好后的模型从一张纯高斯噪声中还原一张图像。
生成模型
下面的内容是前期的知识储备
高斯分布
为什么使用高斯分布?
任何复杂的分布都可以用高斯分布来表示
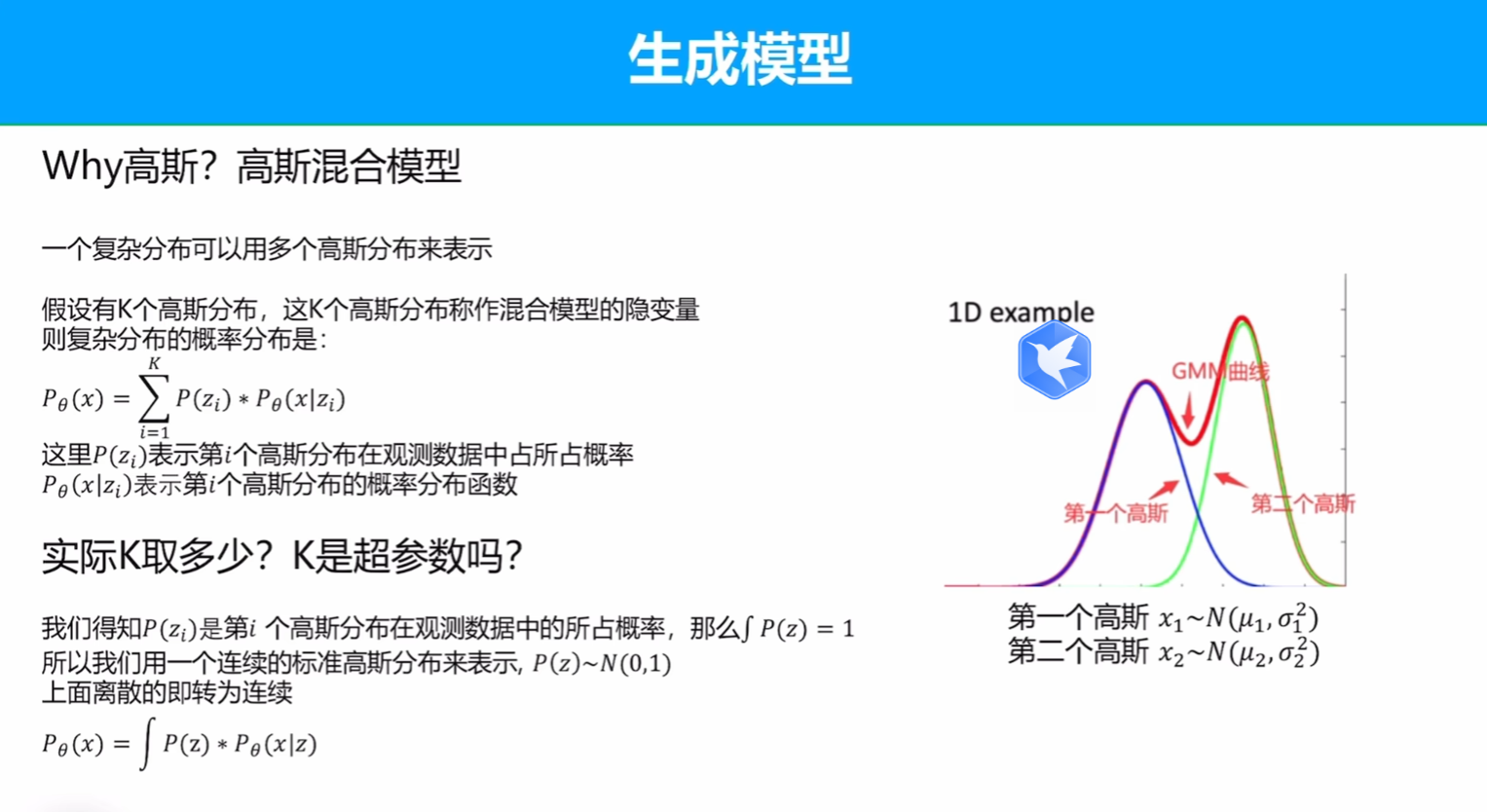
可以看到,高斯函数的加权和还是高斯函数,当加的高斯足够多的时候就可以积分,而权重也可以用高斯分布表示。
最大似然估计
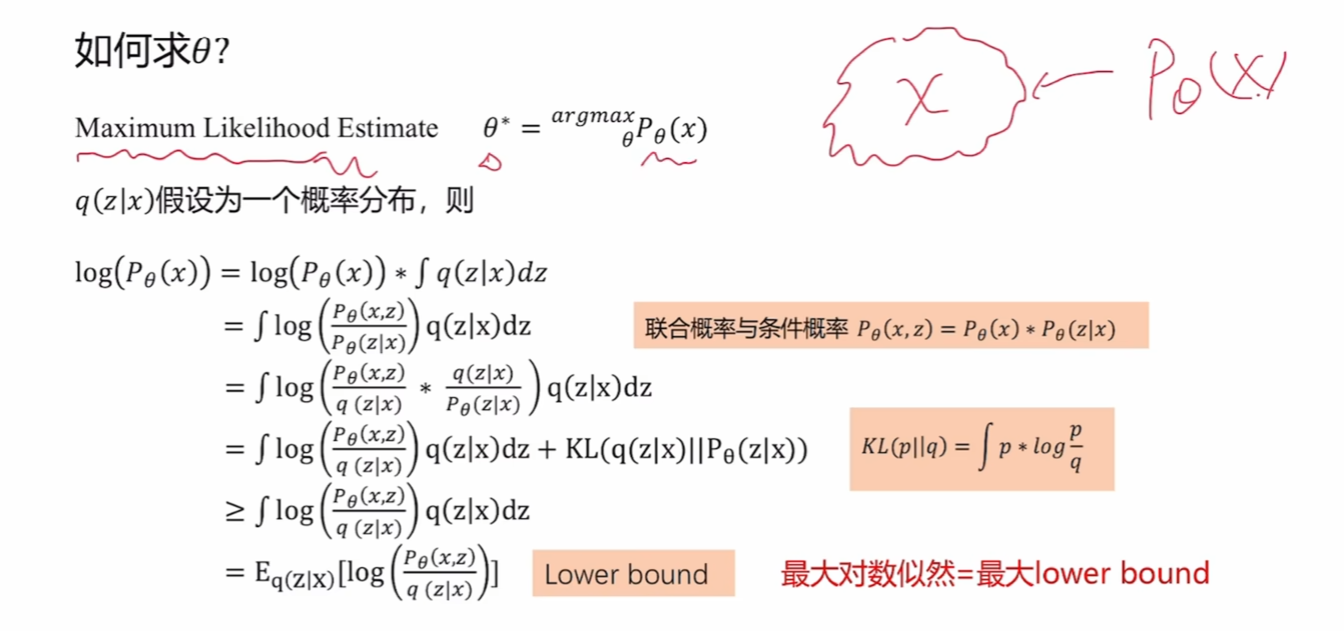
x是我们观测到的数据,按照眼见为实的思想,我们需要调整参数使构建的模型出现观测数据的概率尽可能的大。这里的公式是在求解最大似然估计的下界,是在处理复杂问题时的简化。
DDPM
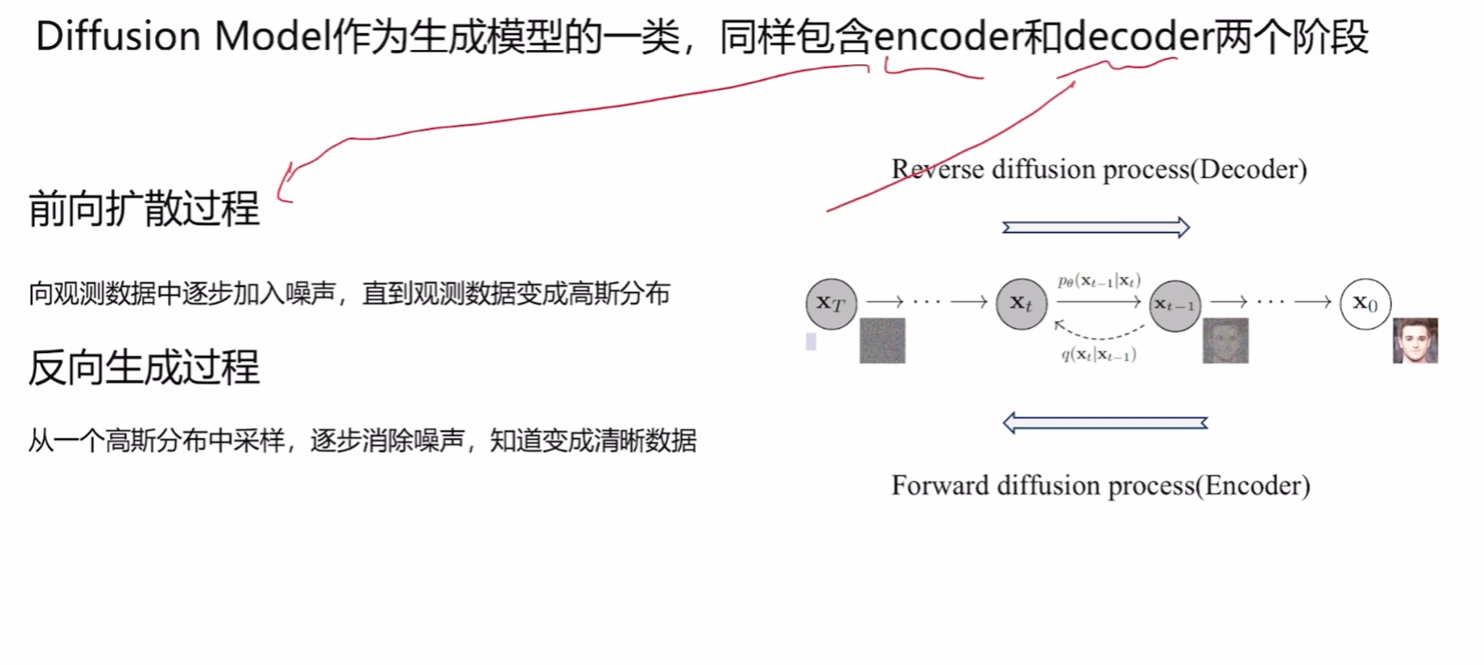
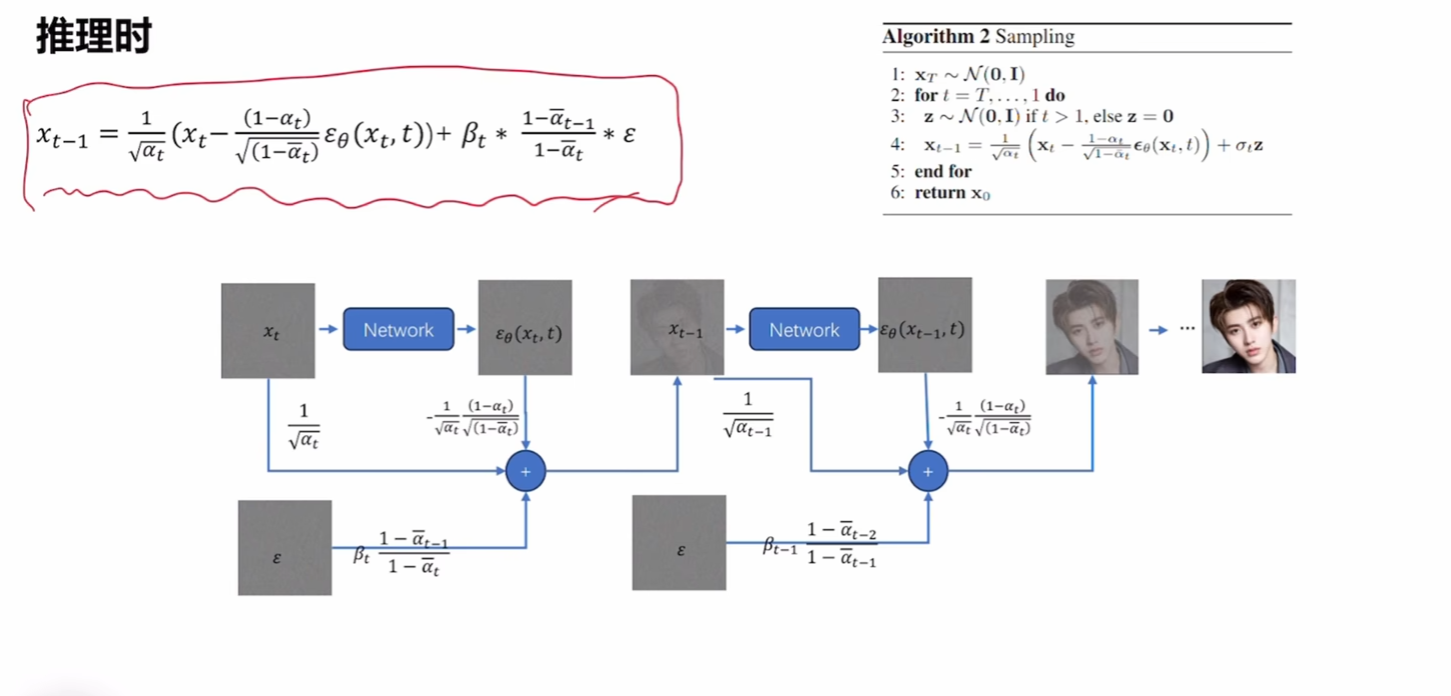
上图内容为基本过程,注意p,q分别表示了前向传播和生成任务。
前向传播
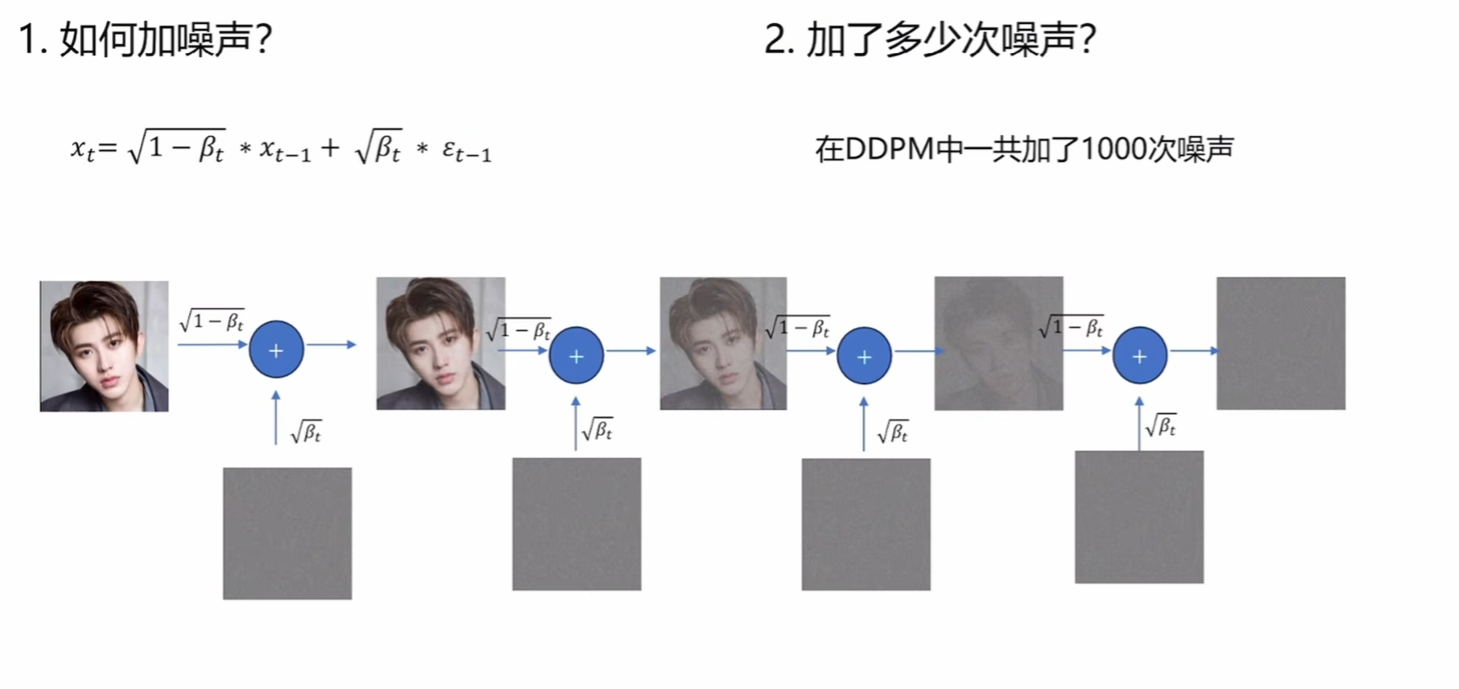
前向传播通过上述的式子,不断地在图片中增加噪声。β\betaβ是可以人为设定的超参数。

上图说明只要知道一个高斯分布的均值和方差就能用标准方差将其表示。
因此,可以写出加噪后图像服从的高斯分布。
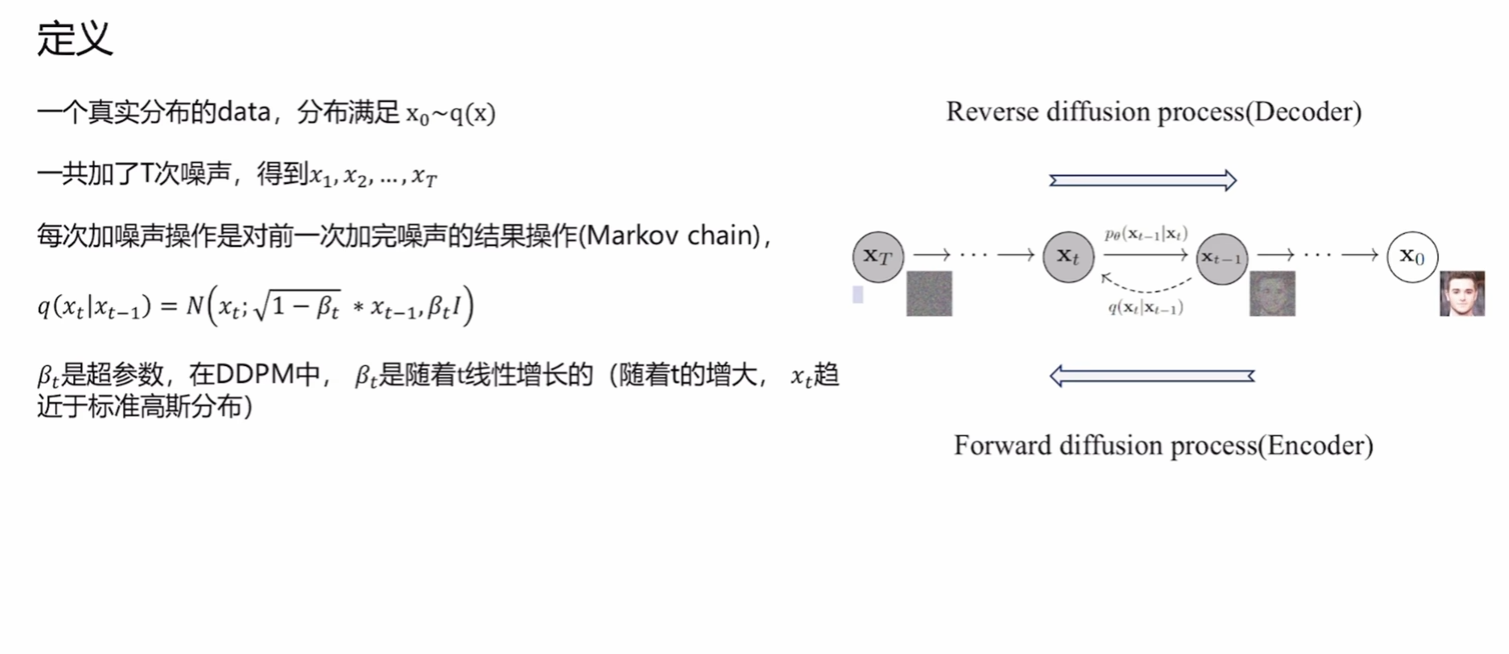
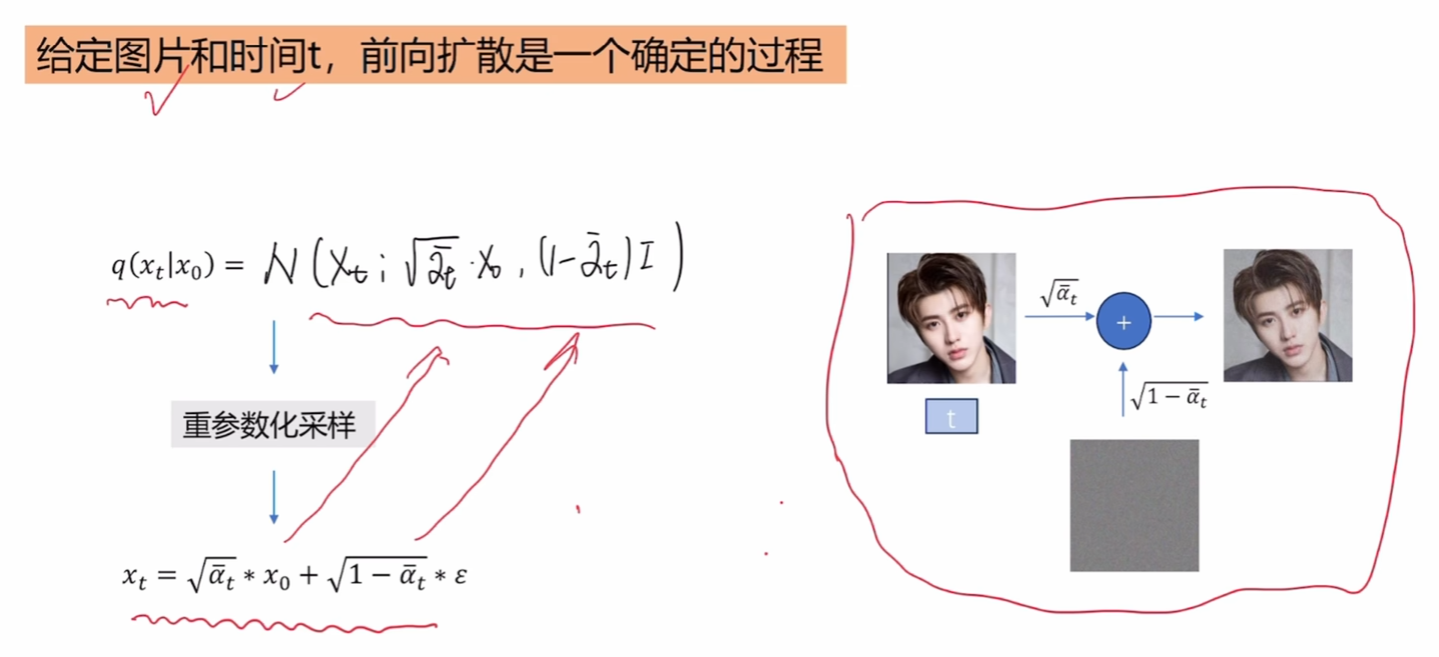
论文中一共做了T = 1000次加噪,由于β\betaβ小于1,最后分布会趋近于标准高斯,具体可看下面这个推导:

反向扩散过程(生成)
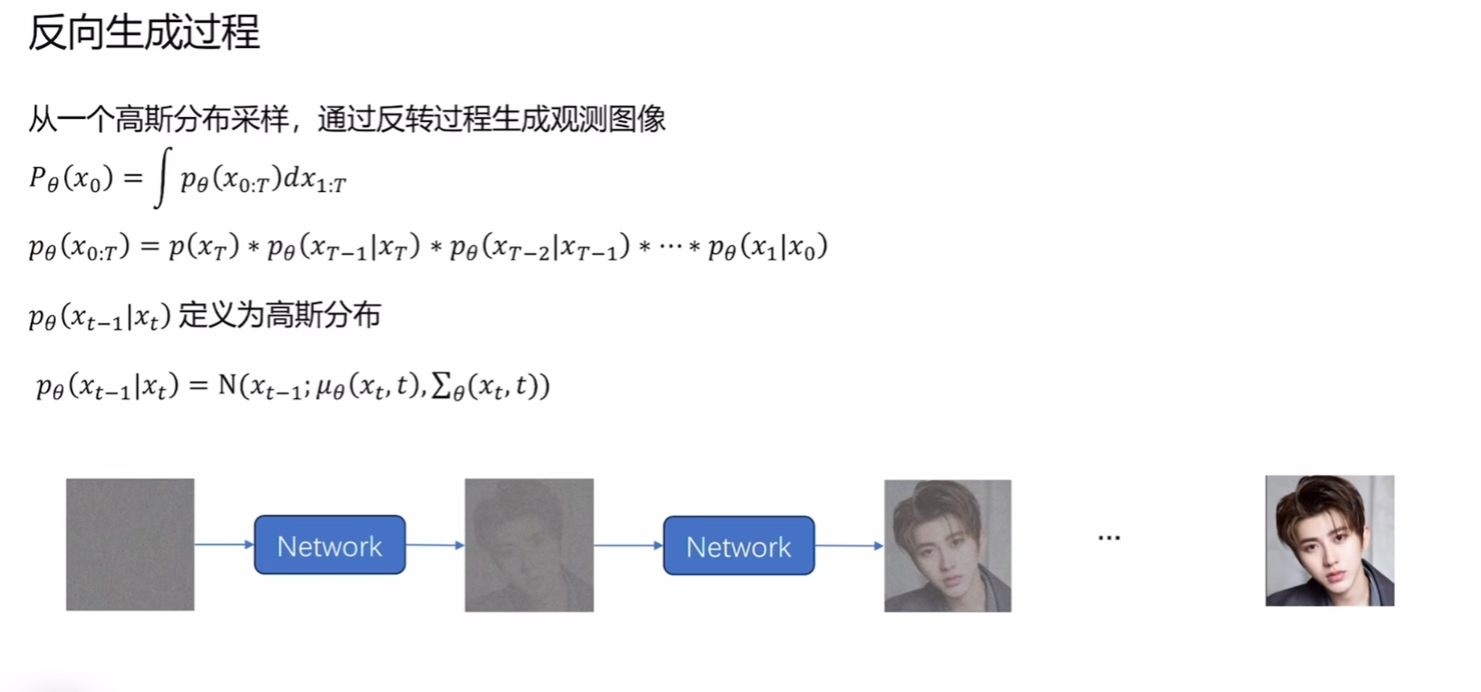
- 第一个式子:计算最终生成的图像,在生成图像的过程中,我们能走很多生成路径,生成出不同的图像,而只有一些路径最终生成x0x_0x0即我们观测到的图像。这个积分的作用就是求生成出观测数据的概率(因为我们要使用最大似然估计)
- 第二个式子:生成x0x_0x0的某一条路径,这其实是一条马尔可夫链,我们要用T个网络恢复成原图,因此要乘以T个分布。
- 为什么定义为高斯分布:为了保持正向和逆向处理一致,前面说明了正向的q就是高斯分布。
- 第四个式子:具体计算,下面给出

注意:这里给出的分布是q,这些都是前向传播中的。为什么这里用前向传播的分布,因为目前还在构建一套数学上可计算的模型。即:正向传播和反向传播应该是可逆的。
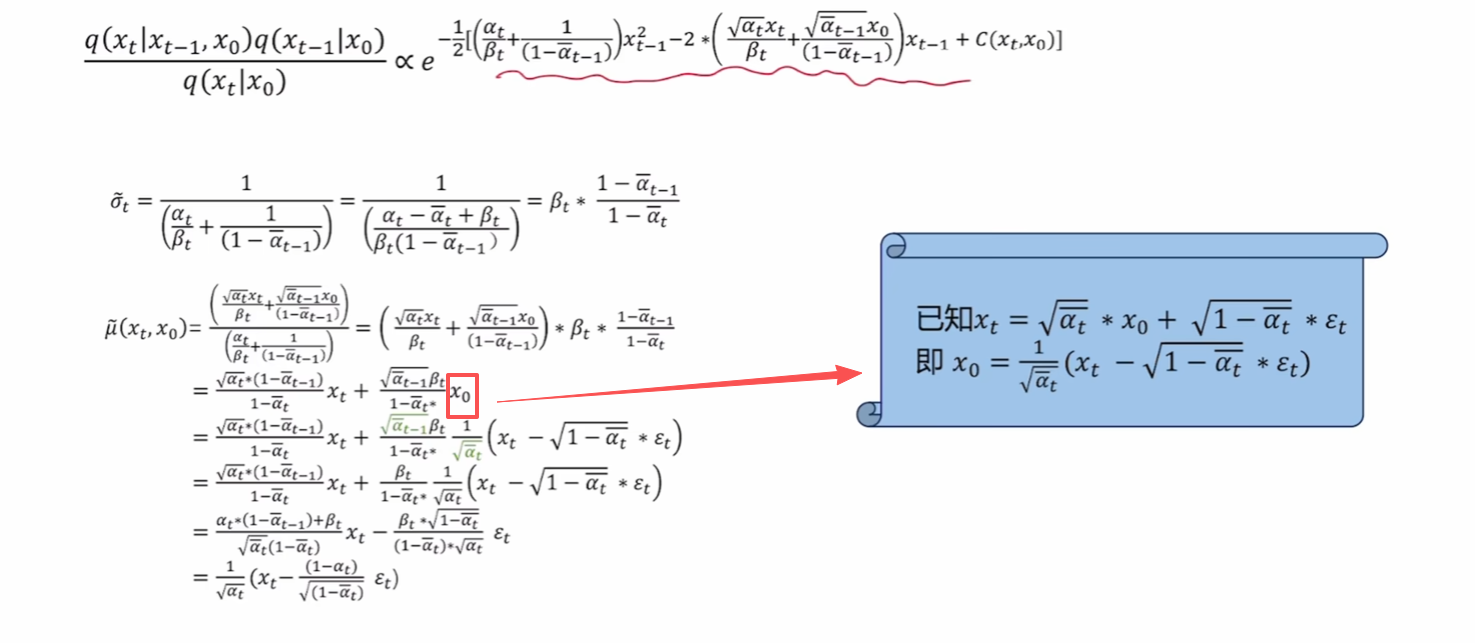
注意式子中x0x_0x0经过了替换。下图为过程的可视化:
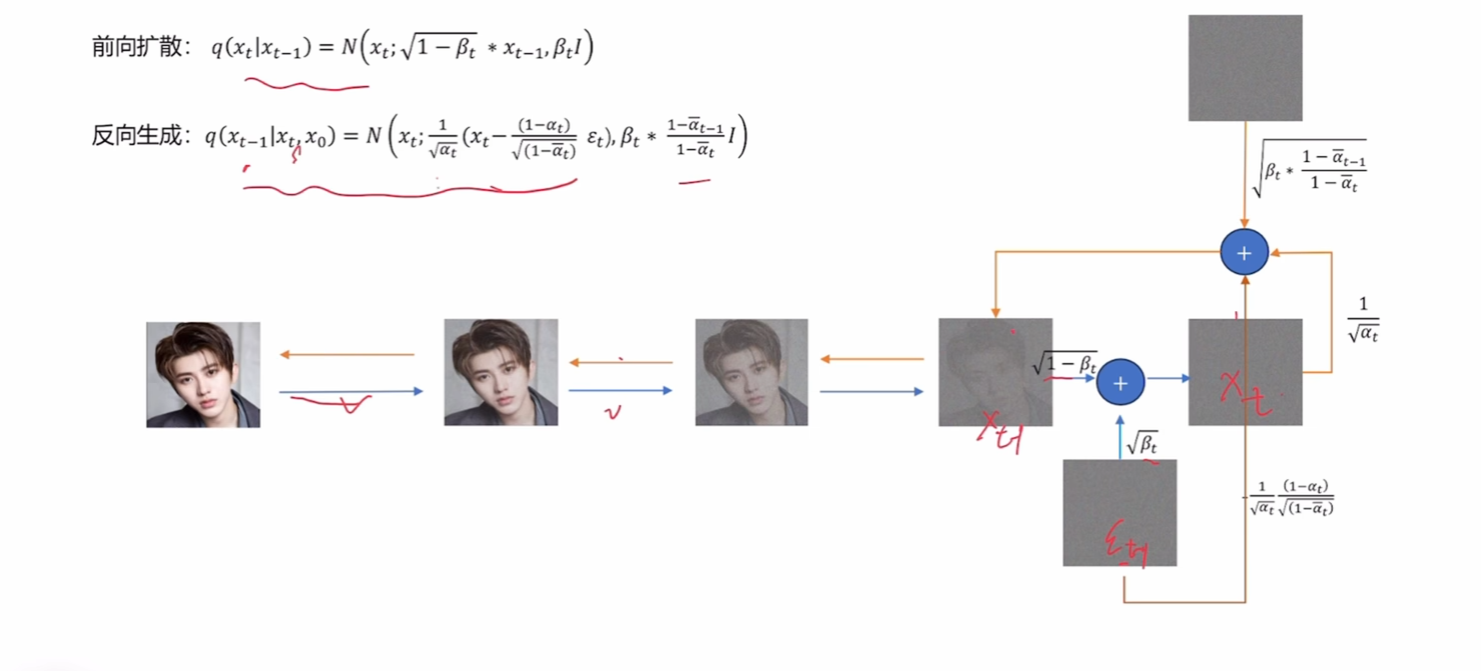
从上图中可以看出,在数学上若想达成这个可逆状态,每一步增加的噪声必须可知。
这样我们就有了明确的优化目标,用模型将每一步的噪声训练出来。
优化目标
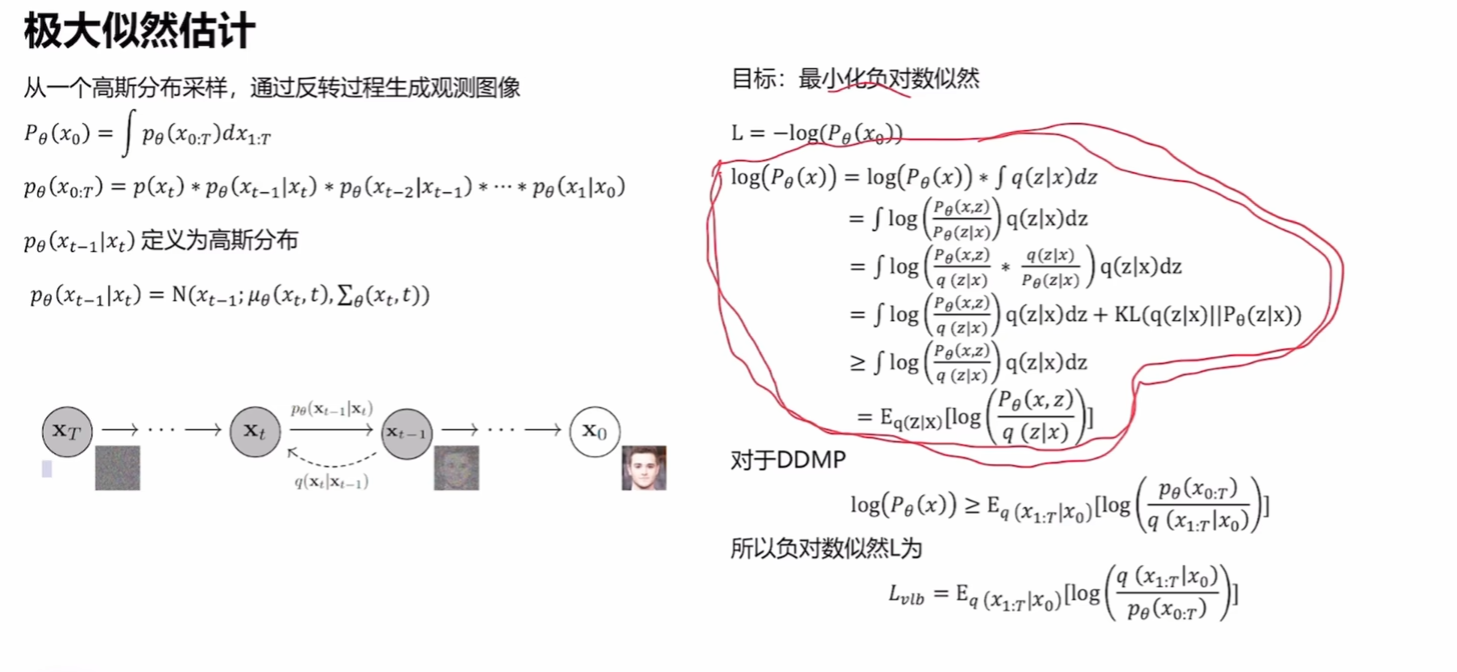
我们通过上面的过程终于得到了x0x_0x0的概率如何表示,这里将其带入极大似然估计中优化。
注意在带入的时候出现了x1x_1x1,因为其于x0x_0x0离得最近
下图中将上面那个式子进一步展开:变成了三部分

- LTL_TLT(重建末端): 比较 xTx_TxT 和标准高斯分布。
- Lt−1L_{t-1}Lt−1(中间步骤): 比较每一个中间步骤 xt−1x_{t-1}xt−1 到 xtx_txt 的一致性。
- L0L_0L0(重建起点): 这就是 x1x_1x1 出现的地方。
重点推导一下中间步骤:

可以看到式子最后的结果就是使上述两个分布的均值和方差一致。而上述两个分布正好就是数学上构建的分布(q)和我们训练的模型的分布(p)
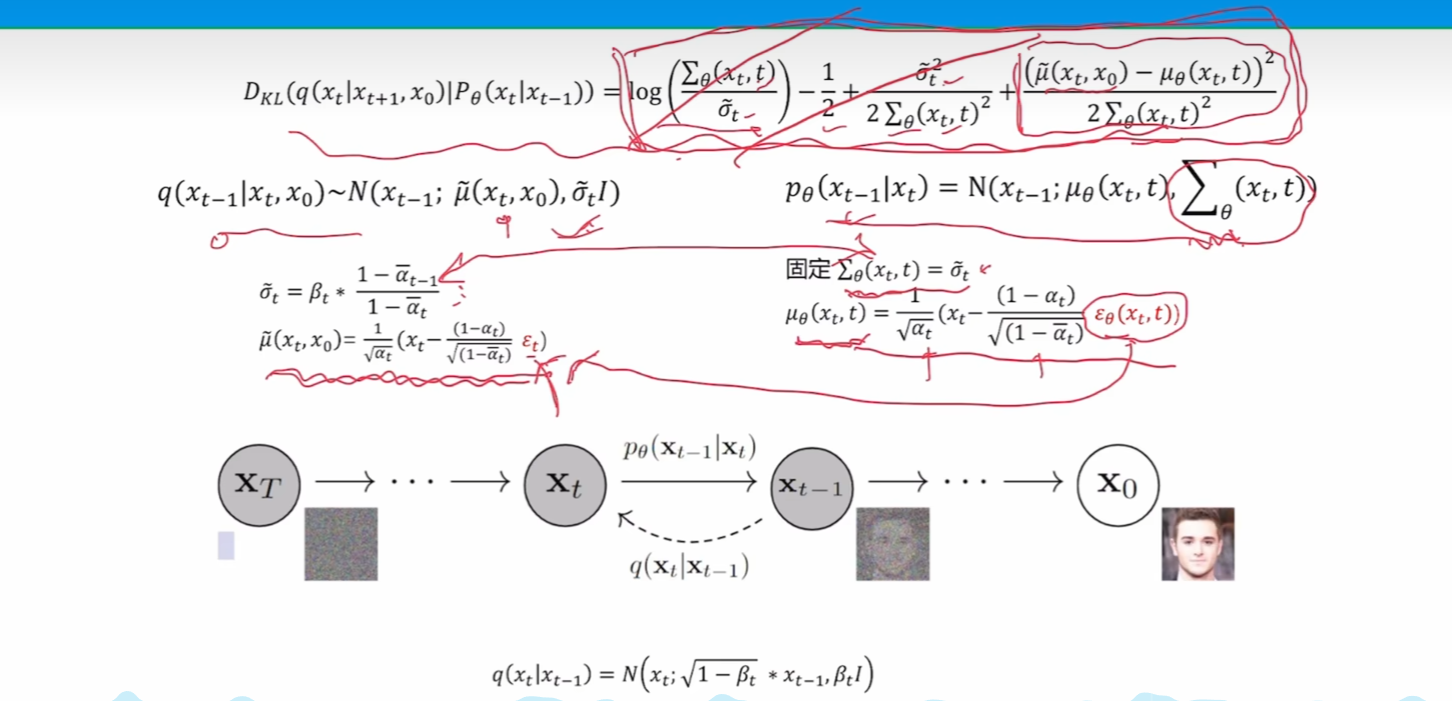
这张图又重新回到了我们的目标,训练预测噪声。 - 方差与噪声无关,直接使两边一致。
- 然后我们按照左边均值的形式为右边构建均值的性质,这样训练才能保证训练出来的噪声一致。
- 而使目标式子为0,则正好能优化我们的优化目标。
结构设计
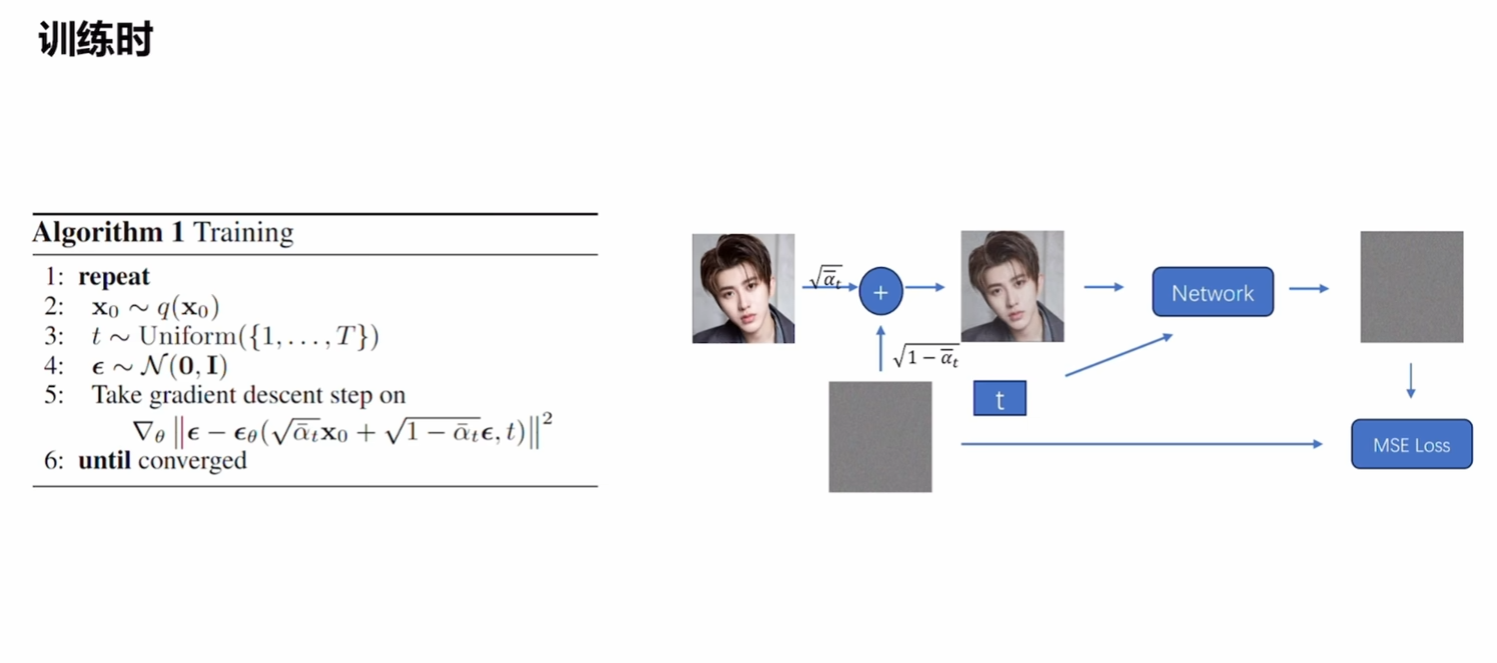
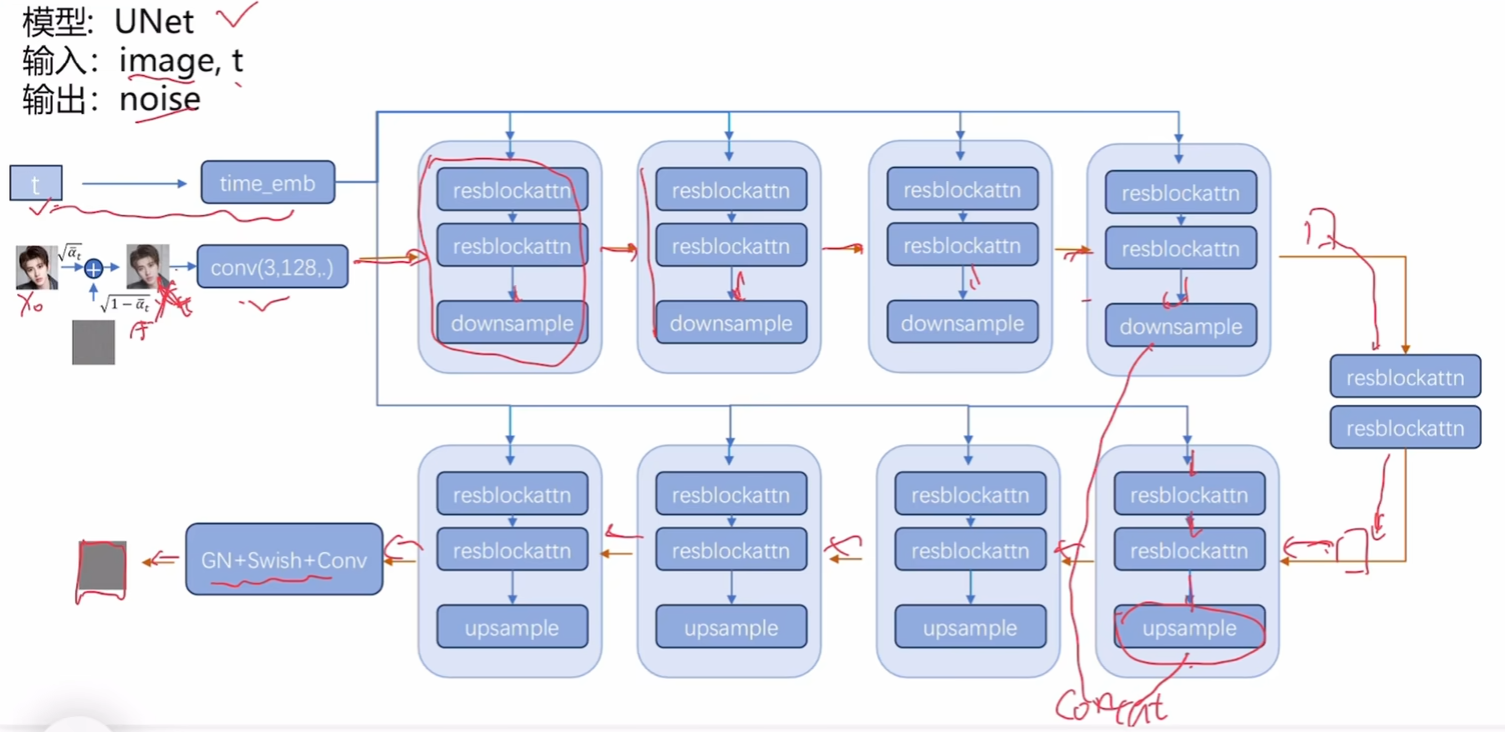
模型设计、
-
Unet:上述网络成一个躺着的u型,所以因此得名。U-Net 是一种深度学习中的卷积神经网络(CNN)架构,最初是专门为医学图像分割(Biomedical Image Segmentation)而设计的。其这样设计的优势是从细到粗再到细。同时掌握了大体信息和局部细节。
-
下采样:比如说池化
-
上采样:比如说双线性插值
-
concat:张量凭借,因为两份信息都有各自用处,不能直接融合。
-
time_emb:时间步嵌入。告诉模型当前是哪一步,方便控制模型每一步干什么
-
GN,swish,conv:GN(组归一化),更小规模的Batch Norm;Swish,激活函数,优化版的rule;Conv (Convolution) ------ 卷积。
代码解读
略
总结
