数据结构 b树（b-树）概念详解

目录

[1. 常见的搜索结构](#1. 常见的搜索结构)

[2. 问题提出](#2. 问题提出)

[3. B-树的概念](#3. B-树的概念)

[4. B-树的插入分析](#4. B-树的插入分析)

5.B-树的删除（思想）

6.B-树的高度

[最小高度 hₘᵢₙ 推导](#最小高度 hₘᵢₙ 推导)

[最大高度 hₘₐₓ 推导](#最大高度 hₘₐₓ 推导)

7.B-树的性能

8.B-树的简单验证（中序遍历）

---

那么在此之前，我们也已经学过很多的搜索结构了，回顾一下：

1. 常见的搜索结构

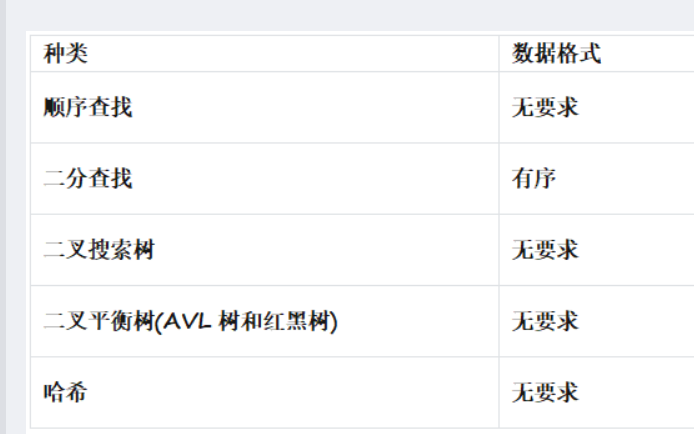
以上结构适合用于数据量相对不是很大，能够一次性存放在内存中，进行数据查找的场景（内查找）。

2. 问题提出

如果数据量很大，比如有100G数据，无法一次放进内存中，那就只能放在磁盘上了，如果放在磁盘上，有时需要搜索某些数据，那么该如何处理呢？

我们可以考虑将关键字及其映射的数据的地址放到一个内存中的搜索树的节点中，当通过搜索树找到要访问数据的关键字时，取这个关键字对应的地址去磁盘访问数据。

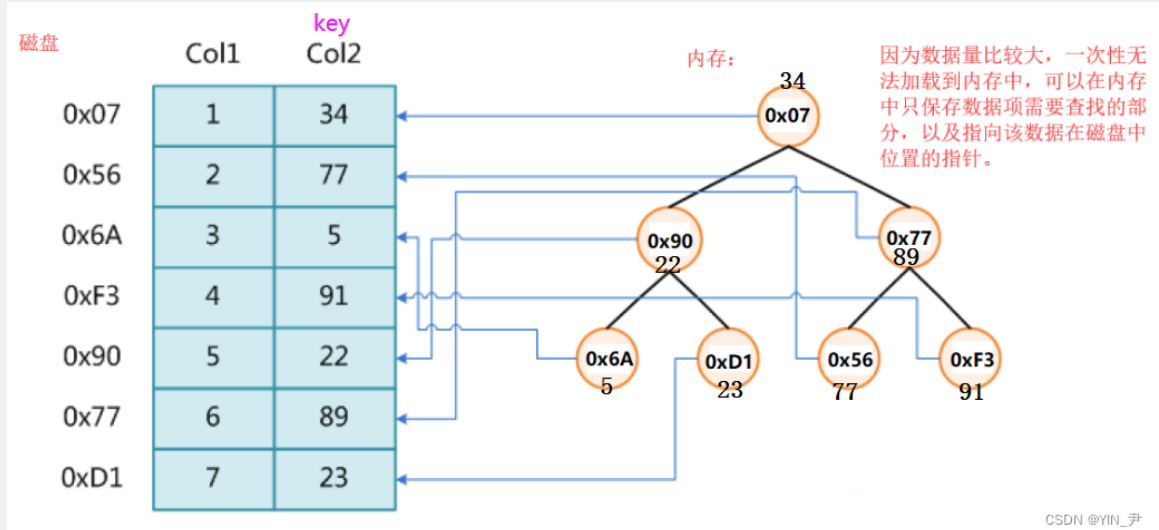
但是呢，实际中我们去查找的这个key可能不都是整型：

可能是字符串比如身份证号码，那这时我们还把所有的key和对应数据的地址都存到内存，也可能是存不下的。

那这时候可以做一个改动：

我不再存储key了，只存储地址

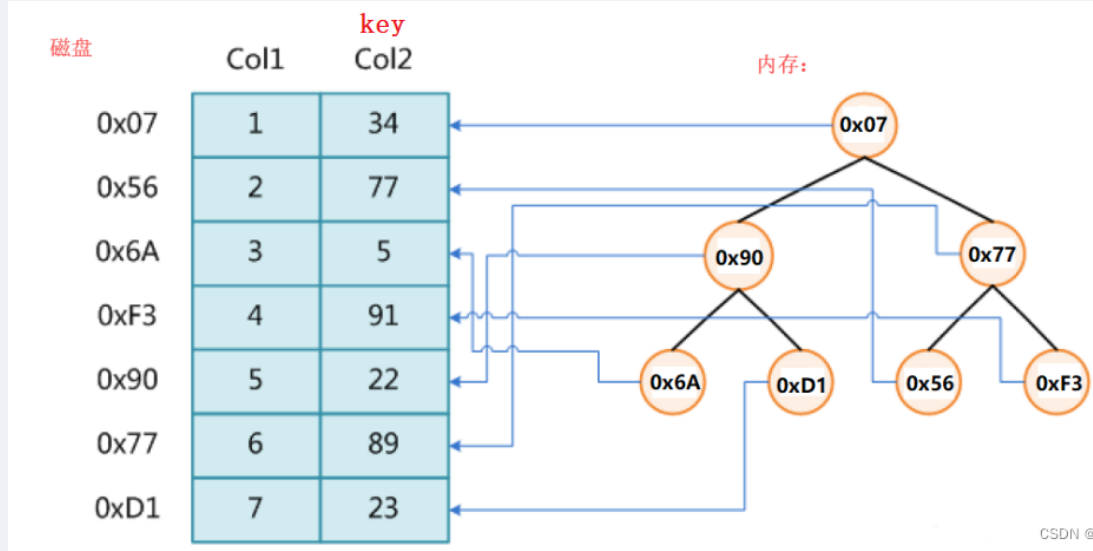
那这样的话我如何判断找到了呢？

那就需要拿着当前的地址去访问磁盘进行判断。
比如现在要找key为77的这个数据，那从根结点开始，首先访问根结点中的地址对应磁盘的数据，是34，那77大于34，所以往右子树找，右子树0x77对应的是89（又一次访问磁盘），77比89小，再去左子树找，左子树地址0x56访问磁盘对应的是77找到了。

那这样做的问题是什么呢？

最坏的情况下我们要进行高度次的查找，那就意味着要进行高度次的磁盘IO。
如果我们使用红黑树或者AVL树的话，就是O(log以2为底N)次。
那如果是在内存中的话，这个查找次数还是很快的，但是现在数据量比较大是在磁盘上存的，而磁盘的速度是很慢的。

所以：

使用平衡二叉树搜索树的缺陷

平衡二叉树搜索树的高度是logN，这个查找次数在内存中是很快的。但是当数据都在磁盘中时，访问磁盘速度很慢，在数据量很大时，logN次的磁盘访问，是一个难以接受的结果。

那如果用哈希表呢？

使用哈希表的缺陷

哈希表的效率很高是O(1)，但是一些极端场景下某个位置哈希冲突很严重，导致访问次数剧增，也是难以接受的。

那如何加速对数据的访问呢？

1. 提高IO的速度(SSD相比传统机械硬盘快了不少，但是还是没有得到本质性的提升)
2. 降低树的高度------多叉平衡树

那我们今天要学的B-树其实就是多叉平衡搜索树

3. B-树的概念

1970年，R.Bayer和E.mccreight提出了一种适合外查找的树，它是一种平衡的多叉树并且是绝对平衡，称为B树(后面有一个B树的改进版本B+树，然后有些地方的B树写的的是B-树，注意不要误读成"B减树")。

一棵m阶(m>2)的B树，是一棵M路的平衡搜索树，可以是空树或者满足一下性质的树：

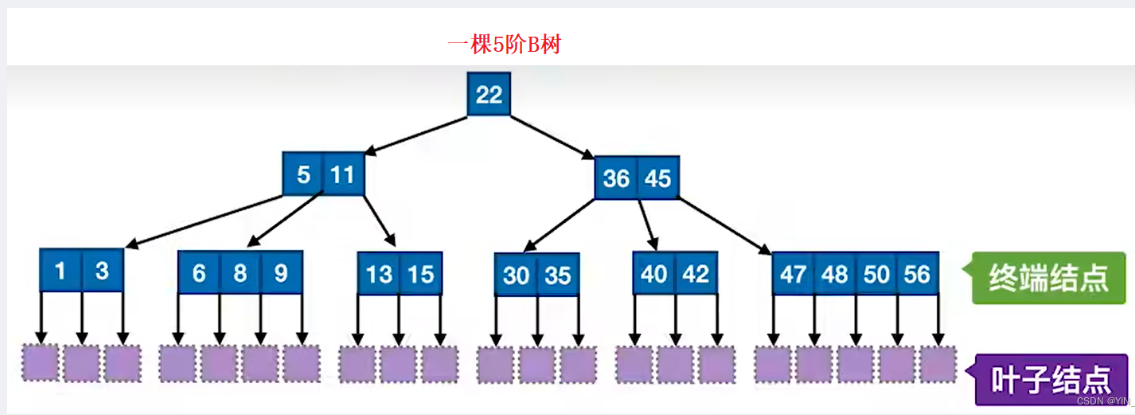
1. m阶B树的每个节点最多有m个分支（子树） ，m-1个元素（关键字）.

2. 根节点最少有两个分支，1个元素 。

3.分节点最少有m/2个分支 ceil(m/2)-1个元素 （ceil是向上取整函数）
ps：该条性质其实保证了让每个结点存储的关键字尽可能多，分叉尽可能多，从而最大限度降低树的高度，如果每个结点只存储一个关键字，其实就退化成我们之前学的平衡搜索树了（根结点是个例外，因为无法保证，比如插入第一个结点，根结点就只有一个结点，无法满足最小值的限制）。至于为什么范围是这样后面会给大家解释。
4. 所有的叶结点都出现在同一层次上，并且不带信息（可以视为外部结点或类似于折半查找判定树的查找失败结点，实际上这些结点不存在，指向这些结点的指针为空)
5. 每个节点中的关键字从小到大（也可以从大到小）排列，节点当中k-1个元素正好是k个孩子包含的元素的值域划分
6. 每个节点的结构为： N = (n, A₀, K₁, A₁, K₂, A₂, ..., Kₙ, Aₙ)，其中 元素严格递增：K₁ < K₂ < ... < Kₙ。关键字在节点中有序排列，每个关键字 Kᵢ 精确划分其左右子树的值域：

左子树(Aᵢ₋₁)：所有值 < Kᵢ

右子树(Aᵢ)：所有值 > Kᵢ

大家可以对照上面的图先来自行理解一下B树的这些性质，等后面我们熟悉了B树的结构之后大家可以再来反复理解这几条性质为什么是这样。

4. B-树的插入分析

那下面我们就来学习一下B-树的插入是怎样的。

那为了方便讲解，也方便大家理解，我们这里选取B-树的阶数取小一点，给一个3：

即三阶B-树（三叉平衡树），那每个结点最多存储两个关键字，两个关键字可以将区间分割成三个部分，因此节点应该有三个孩子（子树）

那每个结点的结构就应该是这样的

但是呢，为了后续实现起来简单，节点的结构如下：

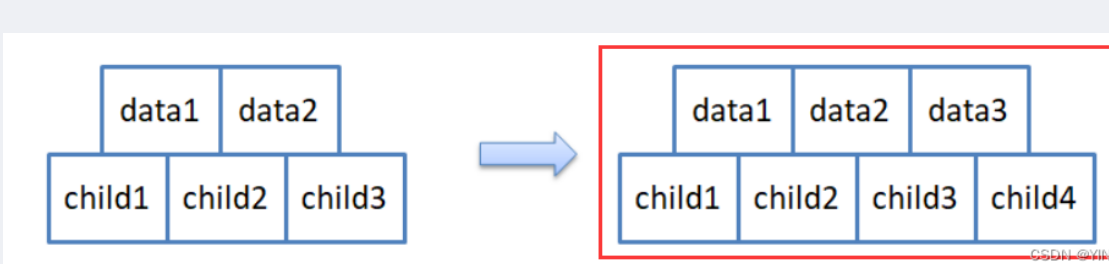
关键字和孩子我们都多给一个空间（后面大家就能体会到为什么要多给一个）

插入过程分析

那下面我们就来找一组数据分析一下插入的过程，用序列{53, 139, 75, 49, 145, 36, 101}构建B树的过程如下：

1. 插入53

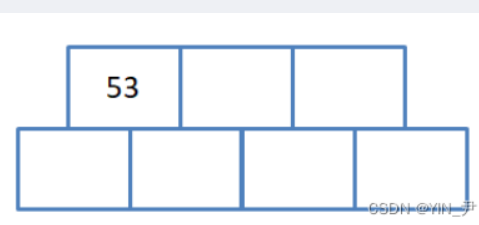
满足B-树的性质，不用动

2. 插入139（关键字我们升序排列）

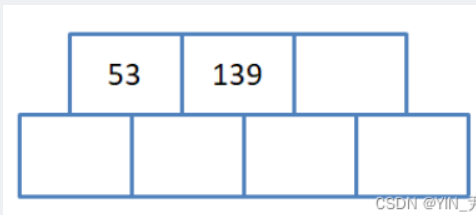
也不用做任何处理

3. 插入75

75插入之后是这样，但是因为我们多开了一个空间，3阶的话每个结点最多3-1=2个关键字。
所以现在这个结点关键字个数超了。

那此时怎么办呢？

要进行一个操作------分裂

怎么分裂呢？

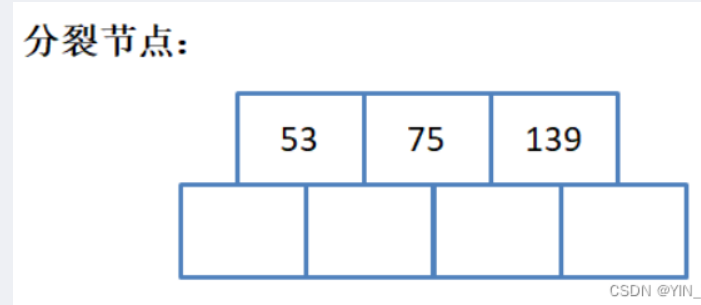
1. 找到关键字序列的中间位置ceil(m/2)，将关键字序列分成两半
2. 新建一个兄弟结点出来，将右半边的关键字分给兄弟结点（左半边留在原结点中）
3. 将中间值提给父亲结点，新建结点成为其右孩子（没有父亲就创建新的根）
为什么中位数做父亲？------满足搜索树的大小关系（左<根<右）
4. 结点指针链接起来

那通过这里大家来体会一下上面的规则中为什么要求除根结点外的所有非叶子结点最少包含ceil(m/2)-1个关键字。
如果m是奇数比如9，那ceil(m/2)是5个，5-1是4，而9个的话分裂之后正好两边每个结点都是4个关键字，中间的一个提取给父亲。
如果是偶数比如10的话，ceil(m/2)是5，5-1是4，而10个分裂的话，肯定不平均，一边4个（最少的），一边5个，还有一个中间值要提取给父亲。
所以它们最少就是ceil(m/2)-1个关键字。

那我们再来插入几个看看：

还是我们上面给的那组数据，再往后插入49，145

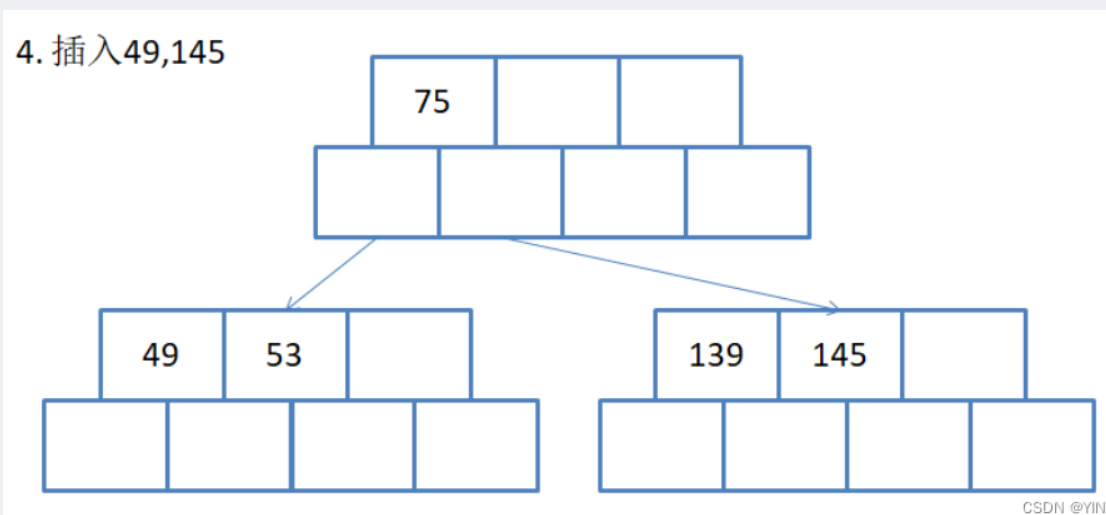
接着再往后，36

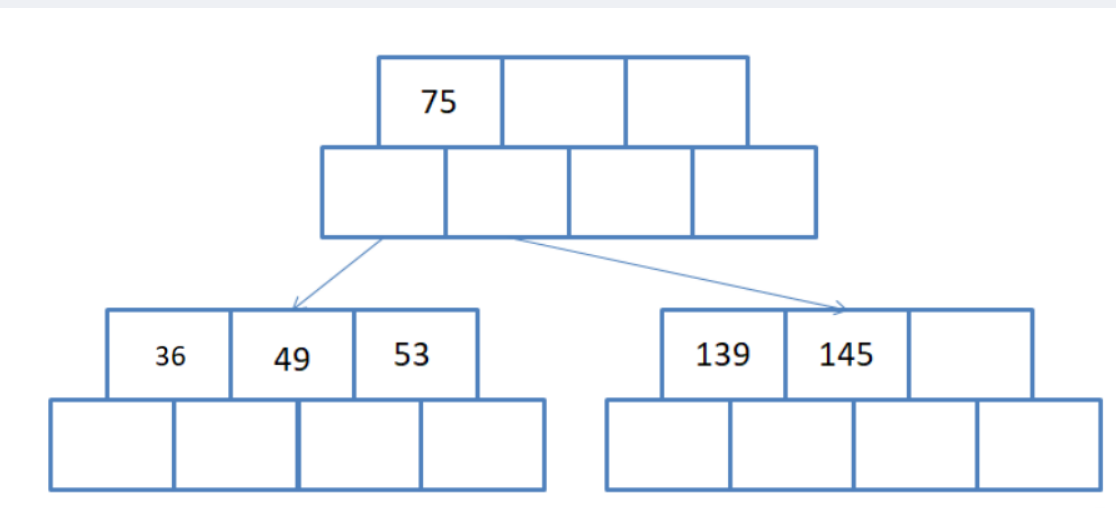
那此时36插入的这个结点又满了，然后就要进行分裂。
大家现在体会，为什么我们要多开一个空间？这样的话我们就可以在插入之后关键字顺序已经调整好的情况下去分裂，就方便很多 。

那然后我们来看这里的分裂怎么做？

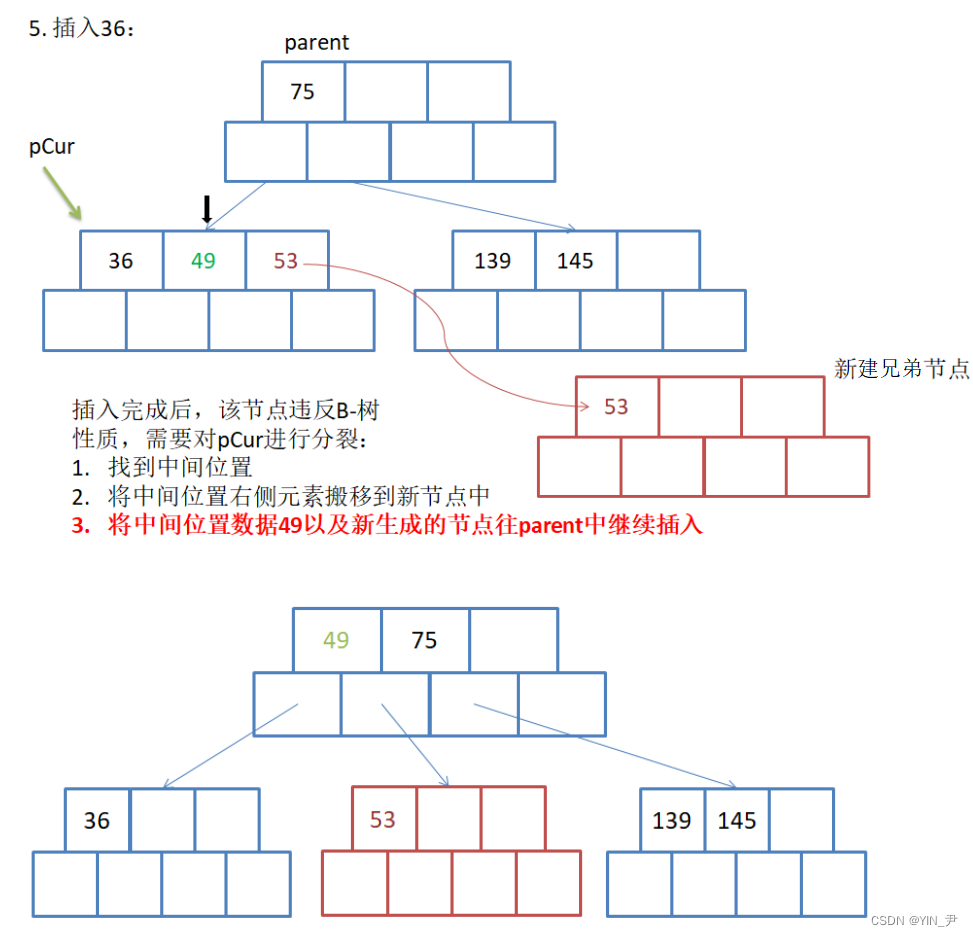
新增一个兄弟结点之后，相当于它们的父亲结点就多了一个孩子，所以也需要增加一个关键字（关键值始终比孩子少一个），就把中间值提给父亲结点 。

49上提插入到父亲，它比75小，所以75往后移（它的孩子也跟着往后移），然后49插入到前面。

再往下插入101：

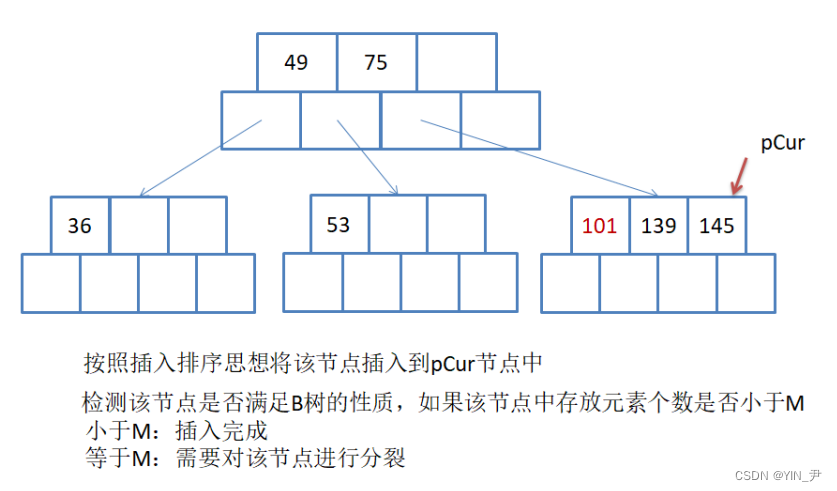
那插入之后这个结点的关键字数量大于m-1了，进行分裂

分裂的步骤还是和上面一样

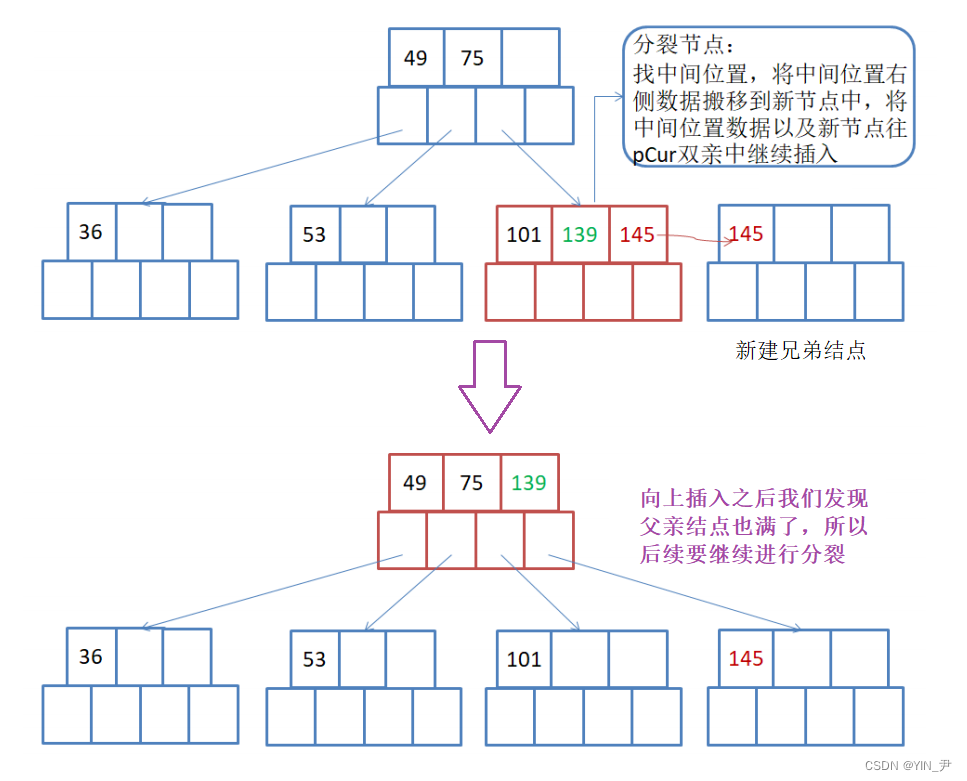
但是此时分裂之后我们发现父亲满了，所以需要继续向上分裂

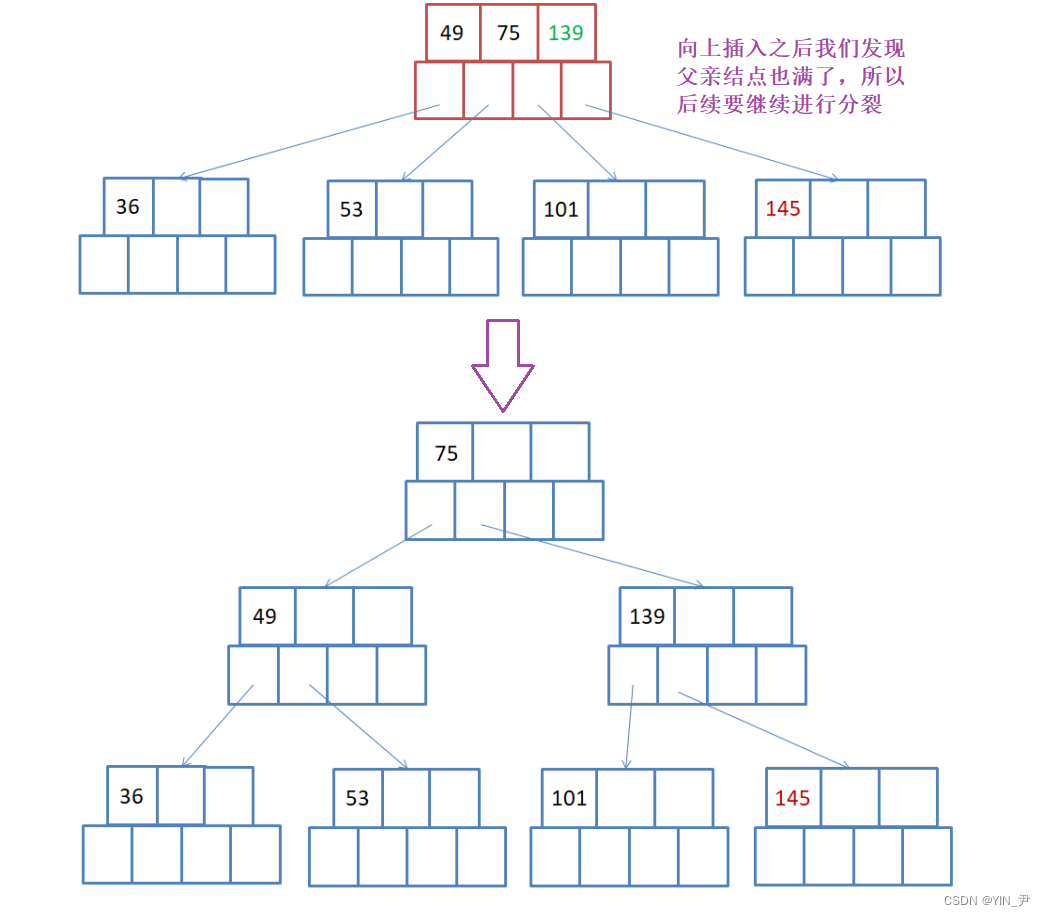
那这就是一个完整的插入过程。
并且我们会发现B-树每一次插入之后他都是天然的完全平衡，不需要像红黑树AVL树那样，插入之后不满足平衡条件了，再去调整。
并且B-树的平衡是绝对平衡。每一棵树的左右子树高度之差都是0。
为什么他能保持天然的完全平衡呢？
通过上面的插入过程我们很容易发现B-树是向右和向上生成的，只会产生新的兄弟和父亲。

插入过程总结
如果树为空，直接插入新节点中，该节点为树的根节点
树非空，找待插入关键字在树中的插入位置(注意：找到的插入节点位置一定在终端节点中)
检测是否找到插入位置(假设树中的key唯一，即该元素已经存在时则不插入)
按照插入排序的思想将该关键字插入到找到的结点中
检测该节点关键字数量是否满足B-树的性质：即该节点中的元素个数是否等于M，如果小于则满足，插入结束
如果插入后节点不满足B树的性质，需要对该节点进行分裂：
申请新的兄弟节点
找到该节点的中间位置ceil(m/2)
将该节点中间位置右侧的元素以及其孩子搬移到新节点中（左侧结点留在原结点）
将中间位置元素（新建结点成为其右孩子）提取至父亲结点中插入，从步骤4重复上述操作

5.B-树的删除（思想）

那下面我们来讲一下删除的思想：

同样也需要分情况讨论：

删除的关键字在非终端结点
处理方法是：
用其直接前驱或直接后继替代其位置，转化为对"终端结点"的删除
直接前驱：当前关键字左边指针所指子树中"最右下"的元素
直接后继：当前关键字右边指针所指子树中"最左下"的元素

比如：

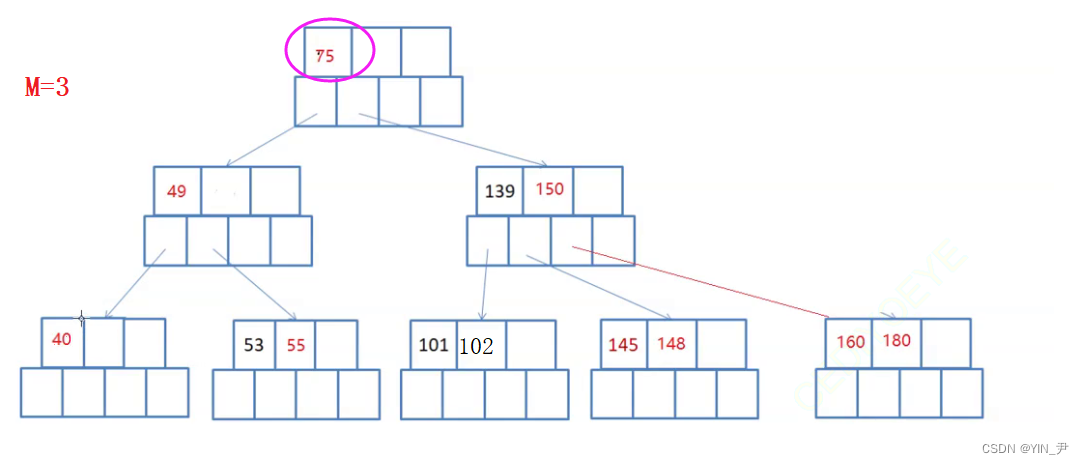
现在要删除75

首先第一种方法可以用直接前驱55替代其位置，然后我们把终端结点里的55删除即可

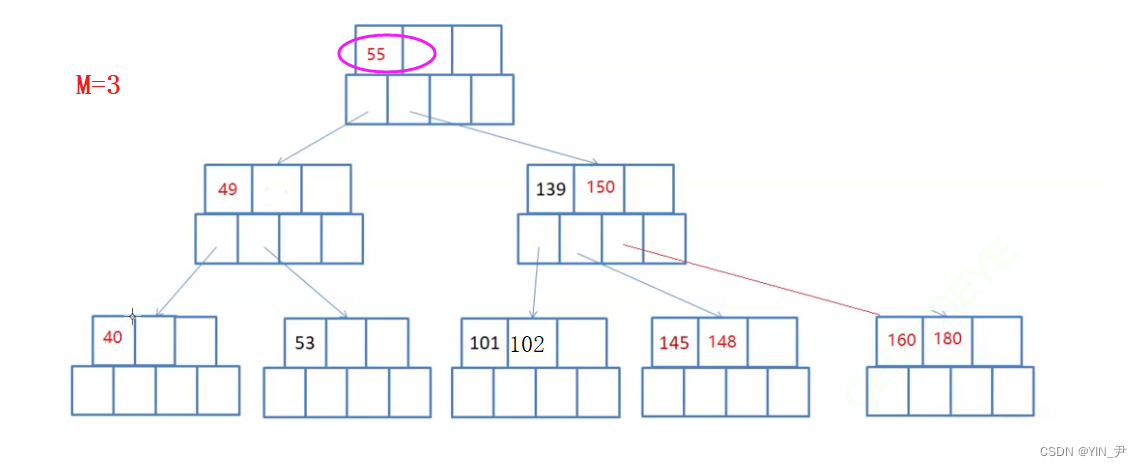
或者用直接后继101替代

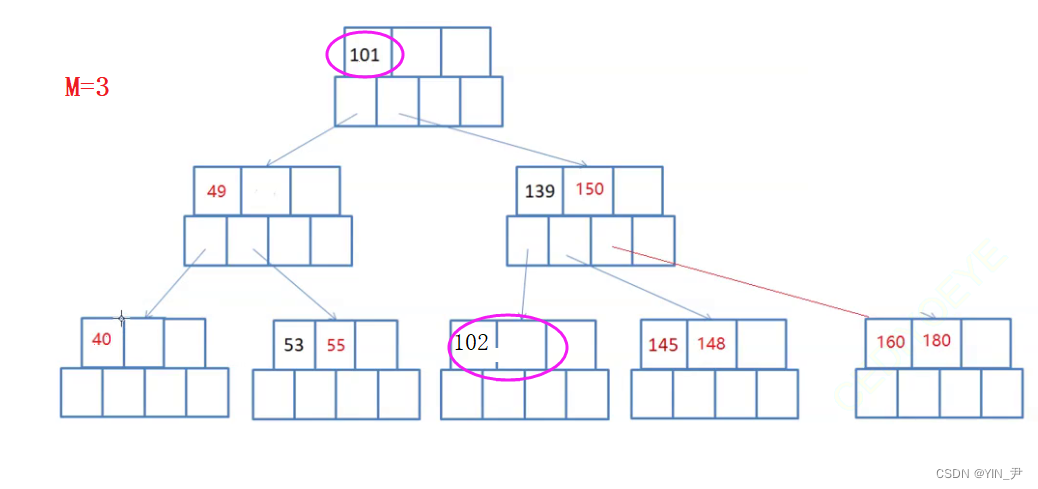
所以对非终端结点关键字的删除操作，必然可以转化为对终端结点的删除

所以下面我们重点来讨论终端结点的删除

删除的关键字在终端结点且删除后结点关键字个数未低于下限
若删除后结点关键字个数未低于下限ceil(m/2)-1，直接删除，无需做任何其它处理

比如：

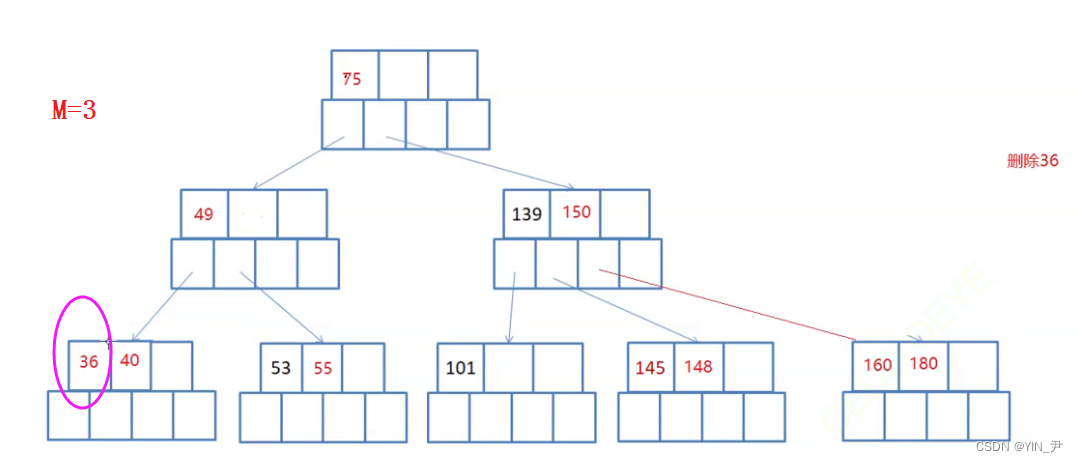
现在要删除36，所在的结点是终端结点，且删除之后，关键字的个数不少于ceil(3/2)-1=1，所以直接删除即可

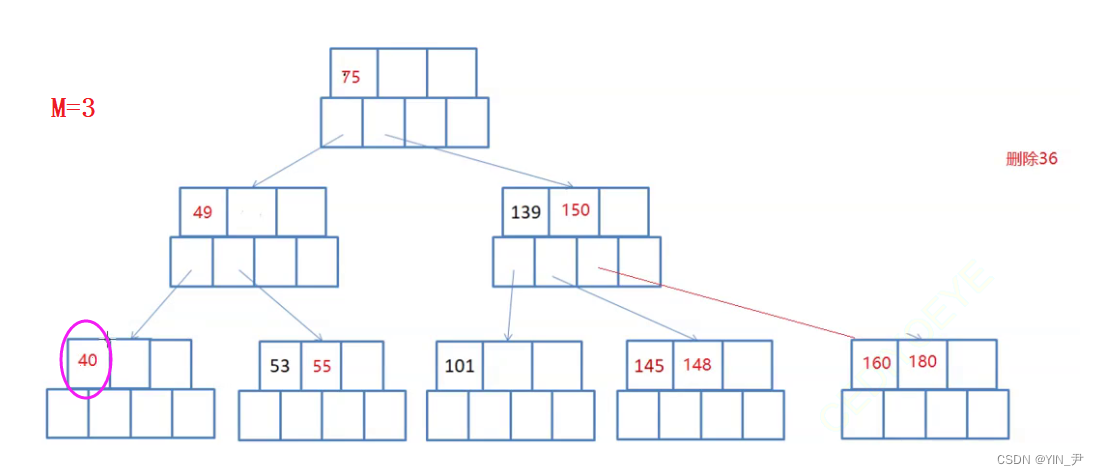
那如果删除之后关键字的个数低于下限ceil(m/2)-1呢？

若删除的关键字在终端结点且删除后结点关键字个数低于下限ceil(m/2)-1

这时候的处理思路是这样的：
删除之后关键字数量低于下限，那就去"借"结点，跟父亲借，父亲再去跟兄弟借
如果不能借（即借完之后父亲或兄弟关键字个数也不满足了），那就按情况进行合并（可能要合并多次）。
最终使得树重新满足B-树的性质。

比如：

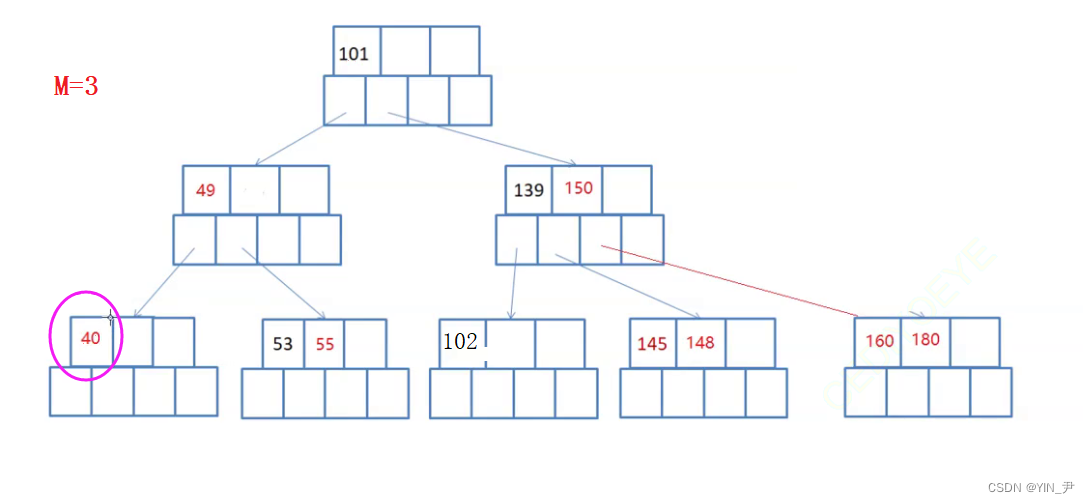
现在要删40，那40删掉的话这个结点关键字个数就不满足性质了，那就去跟父亲借，49借下来，那这样父亲不满足了，父亲再向兄弟借（要删除的那个关键字所在结点的兄弟结点），53搞上去

变成这样

此时就又符合是一棵B-树了
那如果不能借的情况呢？

比如：

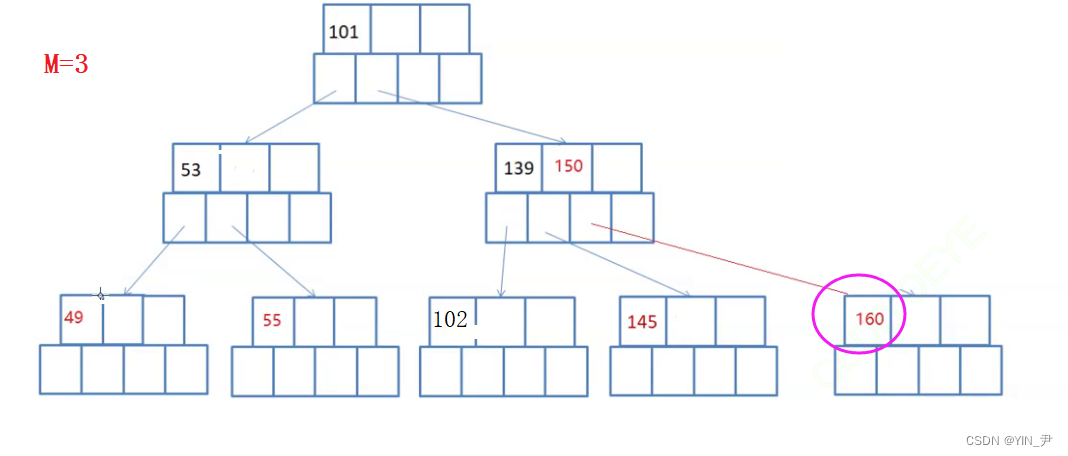
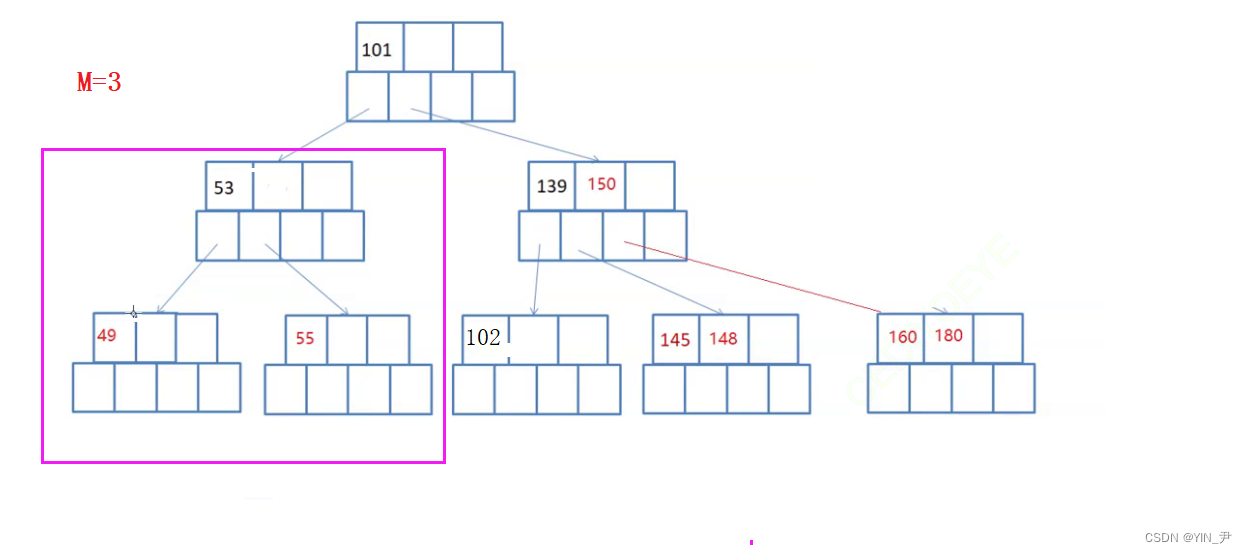
现在要删除160

160如果跟父亲借的话，150下来，那父亲不满足了，因为3个孩子，必须是2个关键字。而且此时兄弟145所在的这个结点也不能借了。因为此时它只有一个关键字，父亲借走一个的话，就不满足了。

所以此时借结点就不行了，就需要合并了。
如何合并呢？
如果结点不够借，则需要将父结点内的关键字与兄弟进行合并。合并后导致父节点关键字数量-1 ，可能需要继续合并。

那我们先来看这个

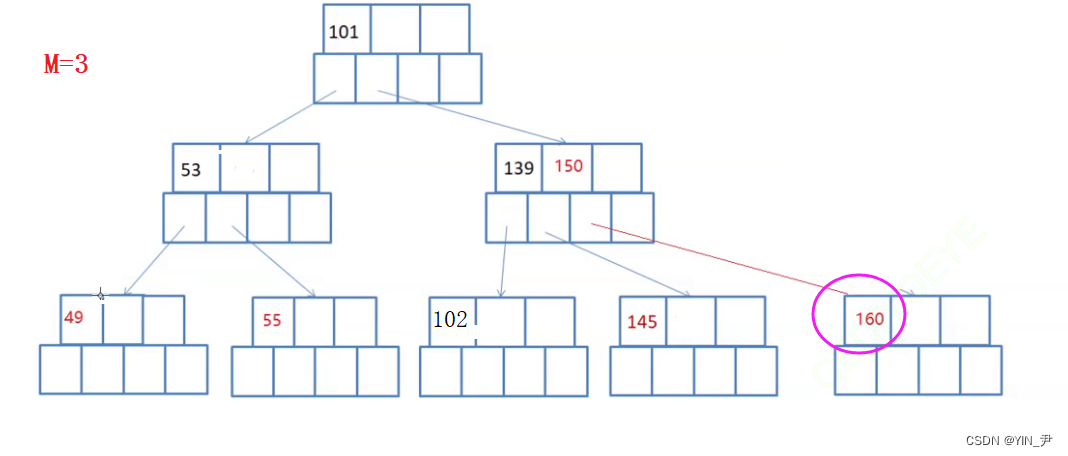
这个情况我们分析了不够借，所以要合并。大家看，160删掉的话，父亲就少了一个孩子，那关键字也应该减少一个，所以可以把父结点的150与145这个孩子合并

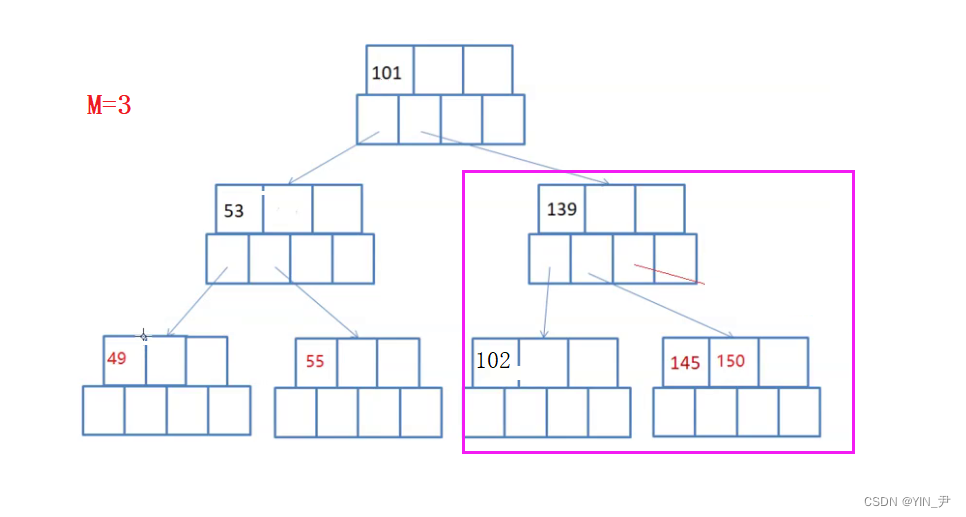
这样就可以了。

当然还有些情况可能需要多次合并：

比如：

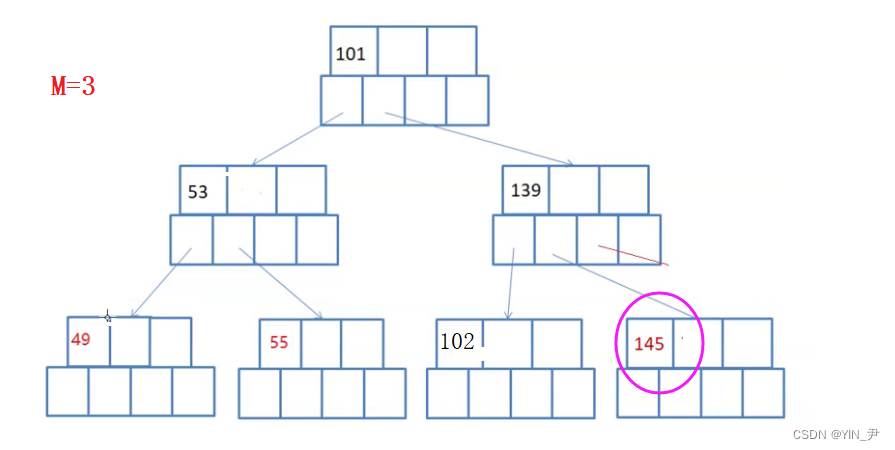
现在要删145，怎么办呢？

肯定是不够借的，所以要合并，确保合并之后依然满足B-树的规则就行了。

大家看这个可以怎么合并：

145干掉之后，左子树这里就不满足了，可以先将139跟102合并。

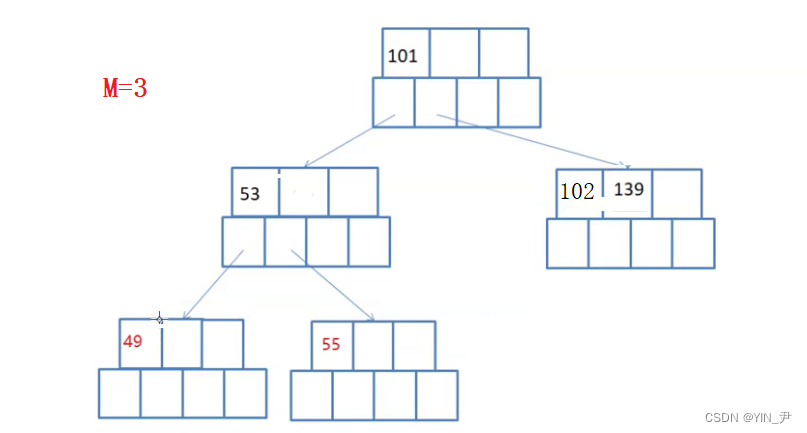
但是此时不平衡了（B-树是绝对平衡的）。

那就要继续合并缩减高度：

很容易看出来，我们可以将101和53合并作为根，这个正好两个关键字，3个孩子

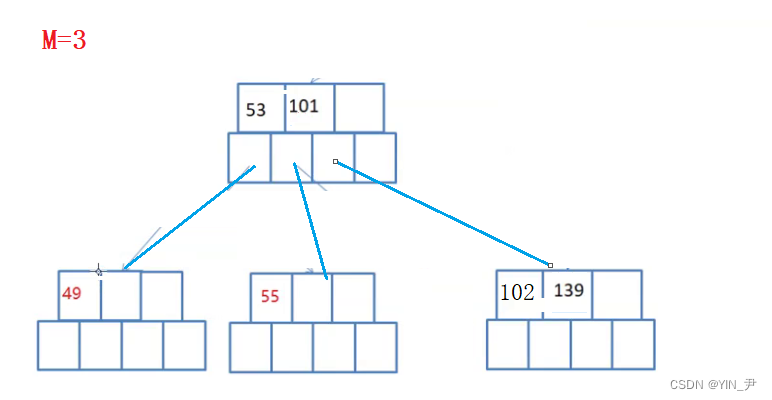
就可以了

6.B-树的高度

问：含n个关键字的m阶B树，最小高度、最大高度是
多少？（注：大部分地方算B树的高度不包括叶子结点即查找失败结点）

最小高度 hₘᵢₙ 推导

前提条件：为了最小化高度，每个节点尽可能满

• 每个节点最多 m 个子树，m-1 个关键字

• 所有节点（包括根）都达到最大容量

推导过程：

第1层（根）：1个节点，最多 m-1 个关键字
第2层：最多 m 个节点，每个最多 m-1 个关键字 → m(m-1) 个关键字
第3层：最多 m² 个节点 → m²(m-1) 个关键字
...
第h层：最多 mʰ⁻¹ 个节点 → mʰ⁻¹(m-1) 个关键字

总关键字数 n：

n = (m-1) × (1 + m + m² + ... + mʰ⁻¹)
  = (m-1) × (mʰ - 1)/(m - 1)  [等比数列求和公式]
  = mʰ - 1

解得最小高度：

mʰ = n + 1
h = logₘ(n + 1)

注意 ：这个 h 是树的层数（根在第1层），不是通常说的树高（边数）。

最大高度 hₘₐₓ 推导

前提条件：为了最大化高度，每个节点尽可能空

• 根节点：最少 1 个关键字，2 个子树

• 非根节点：最少 ⌈m/2⌉ 个子树，⌈m/2⌉ - 1 个关键字

关键定义 ：

设最小度数 t = ⌈m/2⌉，则：

• 根节点：最少 2 个子树（t ≥ 2）

• 非根节点：最少 t 个子树，t-1 个关键字

推导过程（基于叶子节点数）：

定理：n个关键字的B-树有 n+1 个叶子节点

第1层（根）：1个节点，最少2个子树
第2层：最少2个节点
第3层：每个第2层节点最少t个子树 → 最少2t个节点
第4层：最少2t²个节点
...
第h层（叶子层）：最少2tʰ⁻²个节点

总叶子节点数：

叶子数 = 2 × tʰ⁻² ≥ n + 1

解得最大高度：

tʰ⁻² ≥ (n + 1)/2
h - 2 ≥ logₜ[(n + 1)/2]
h ≤ logₜ[(n + 1)/2] + 2

当然也可以算出关键字的总个数来求解：

上面我们已经知道每层的结点个数，然后我们知道根结点最少一个关键字，其它结点最少k-1个关键字，k最小是ceil(m/2)

那么第一层就是1个关键字，第二层往后就是该层的节点个数*每个结点的最小关键字个数(k-1)

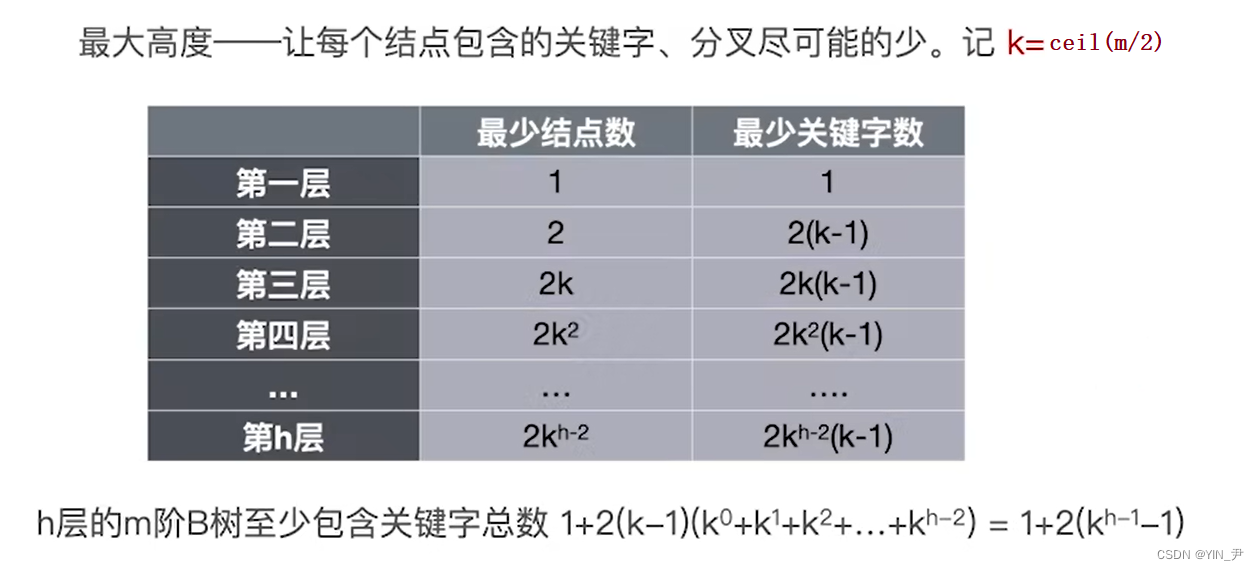
那么因此就有n=1+2(kh-1-1）

同样解得最大高度：

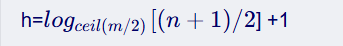
当 m=2 时（B-树退化为二叉搜索树）：

• t = ⌈2/2⌉ = 2

• 最小高度：log₂(n+1)-1 ≈ log₂n

• 最大高度：log₂((n+1)/2)+1 ≈ log₂n

• 两者相等，即平衡二叉树

实际公式需要向上取整：

hₘᵢₙ = ⌈logₘ(n+1)⌉ - 1
hₘₐₓ = ⌈logₜ((n+1)/2)⌉ + 1

7.B-树的性能

8.B-树的简单验证（中序遍历）

那B-树呢也是搜索树，同样满足左子树<根<右子树，那我们可以对它进行一个验证，看中序遍历是否能得到一个有序序列。

那下面我们就来实现一下B-树的中序遍历：

我们还是来搞一个图对照着分析一下思路：

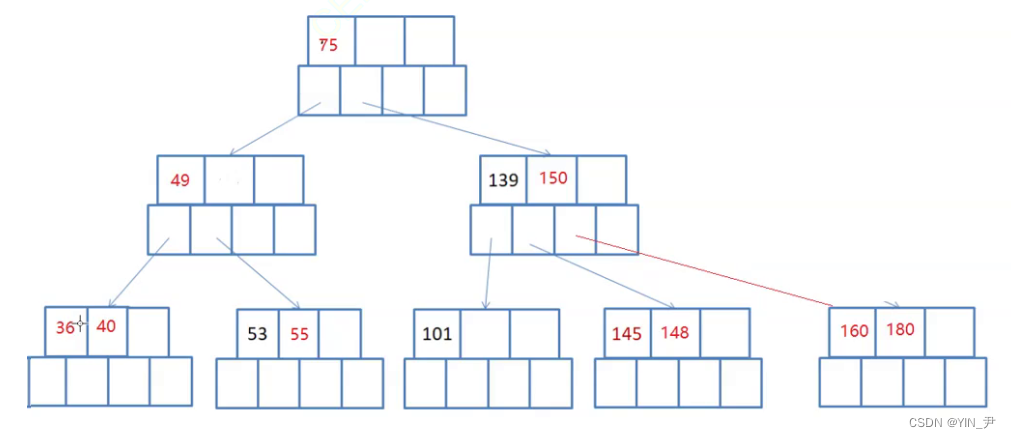
就拿这个来分析：

对于我们之前学的二叉树来说中序遍历的思想是：左子树、根、右子树

那B-树的话它可能是一个多叉的，那它的中序遍历应该怎么走呢？

首先肯定还是先访问左子树，搜索树中最左的结点一定是最小的

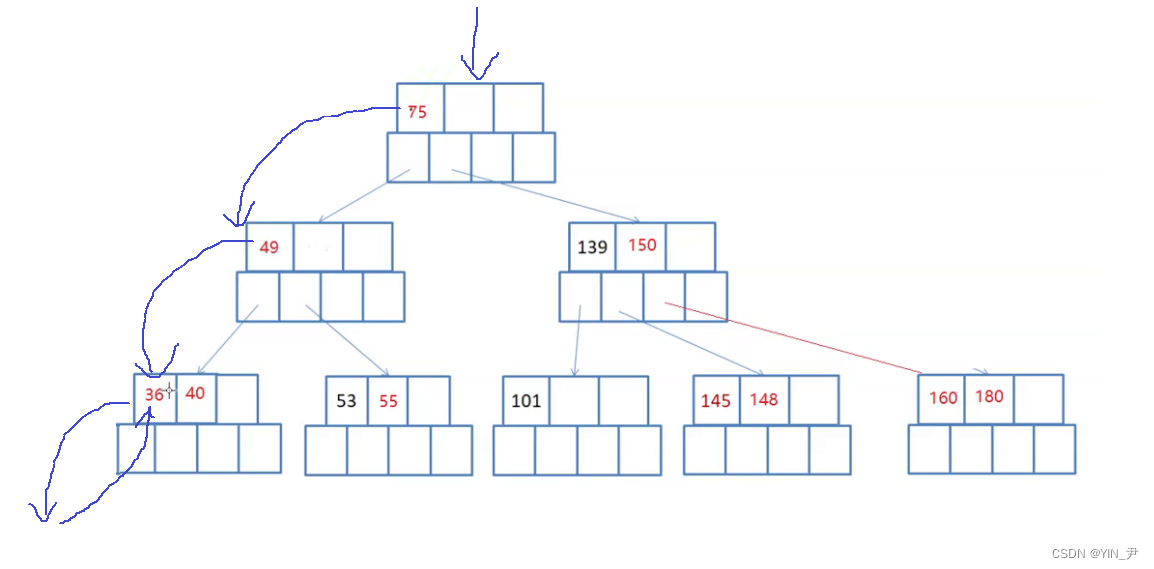
当然如果算上空结点的话最左的应该是空，左子树，然后依然是根，就是36，36就是最小的，没问题。

左子树、根，那然后呢？

是36的右子树吗？可以认为是36的右子树，但是我们要把它当作40的左孩子看。

36这个关键字访问完，就走到后面的40，对于40，同样是先左子树，再根

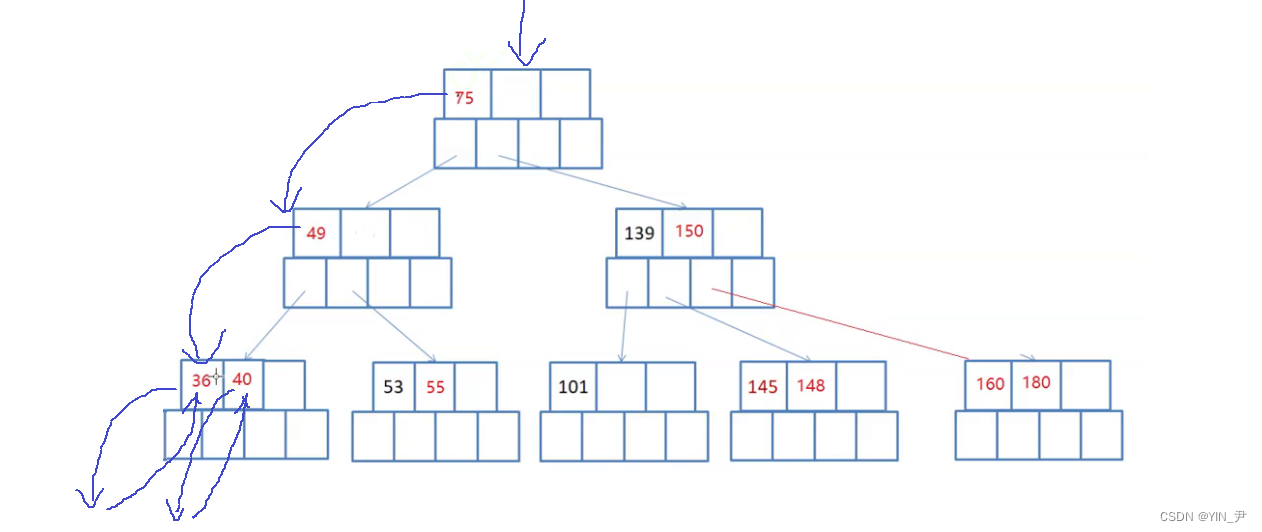
那这个第二个访问到的元素就是40，此时当前结点所有的关键字访问完了，最后再去访问最后一个关键字的右子树：

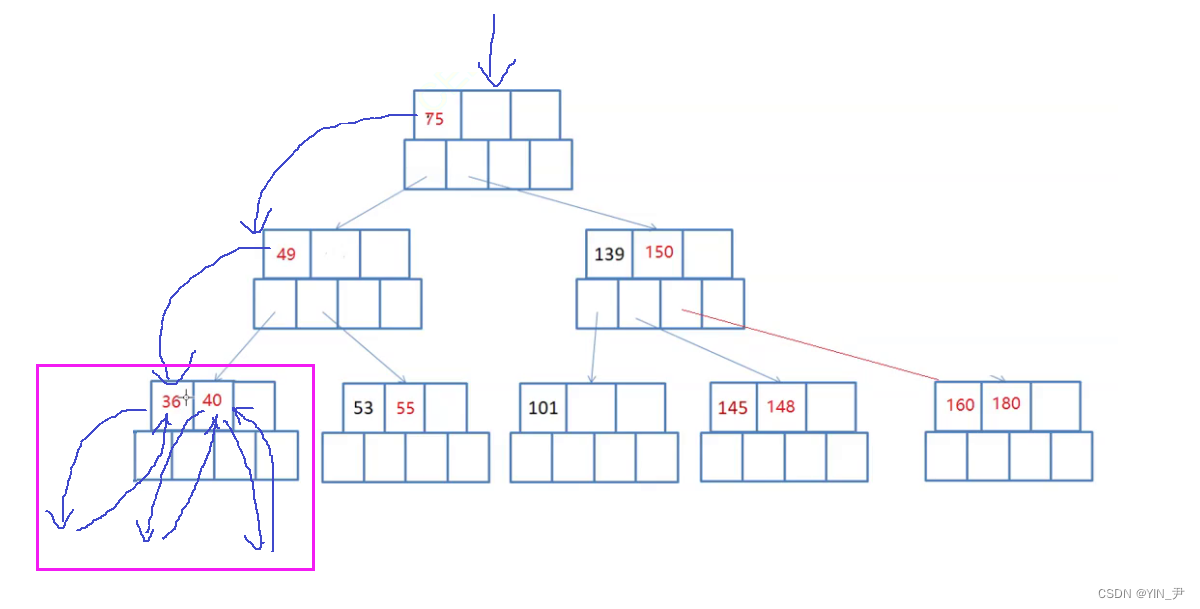
此时整个结点才被访问完。

那此时就相当于是49的左子树访问完了，然后访问根49，后面就是一样的处理...

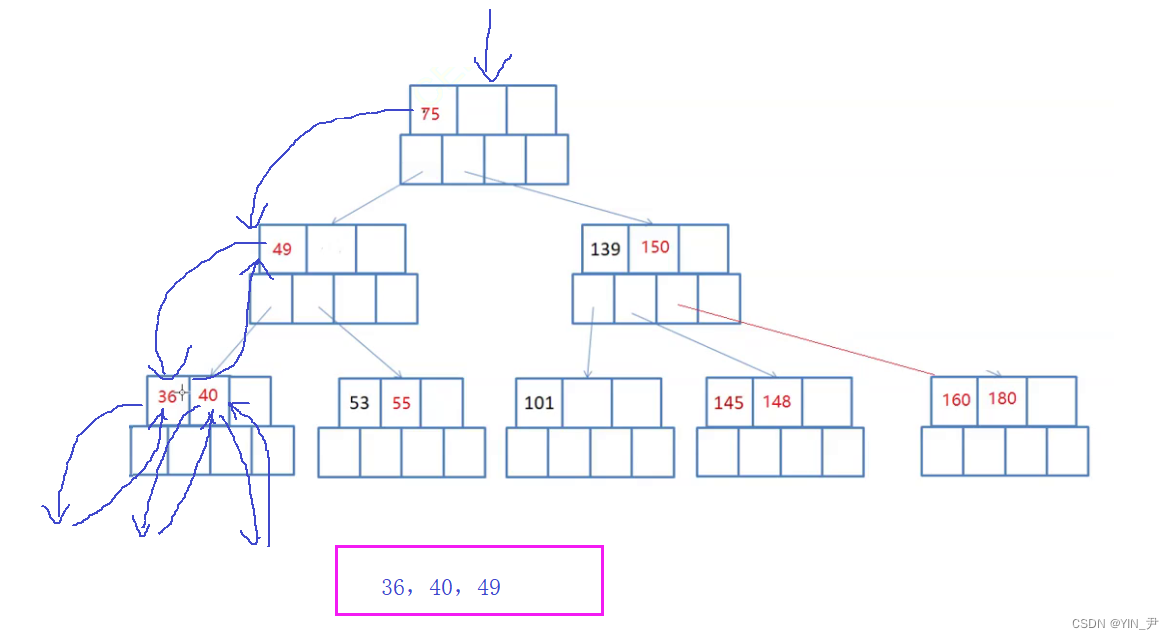
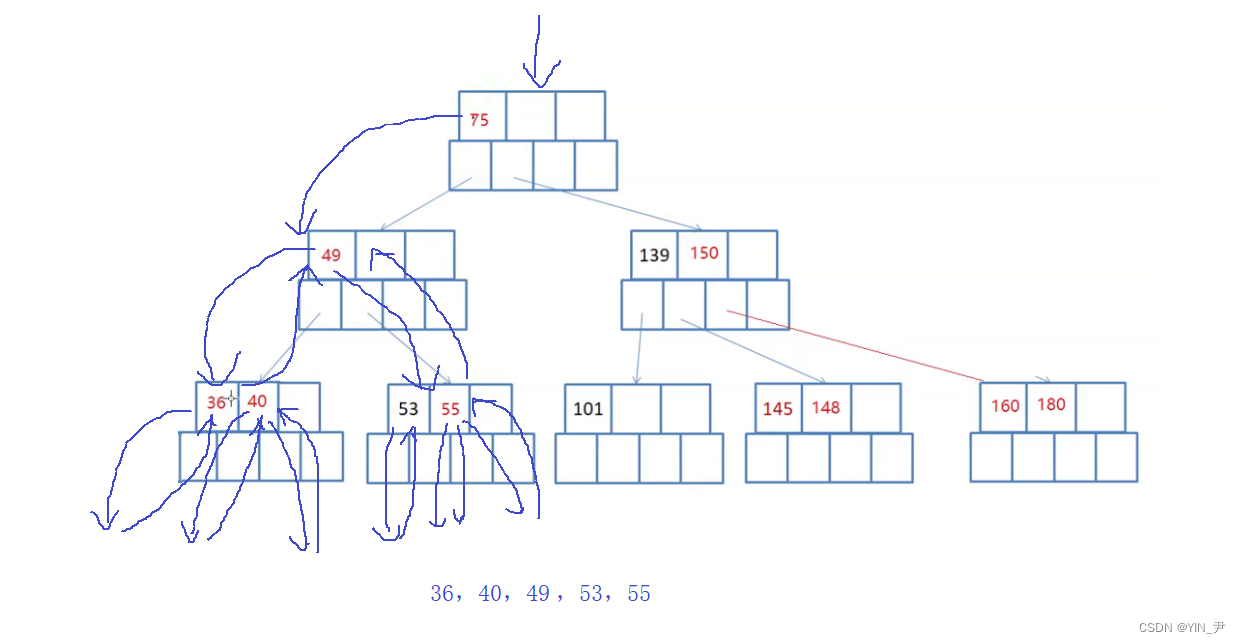
🆗，大家看这样就可以了

所以B-树的中序遍历是怎么样的呢？

左子树、根；（下一个关键字的）左子树、根；（再下一个）左子树、根；...(一直往后直至走完最后一个关键字）；右子树（最后一个关键字的右子树）

左 根 左 根 ... 右