【算法训练营 · 补充】LeetCode Hot100（下）

十八岁讨厌编程2025-12-31 13:40

文章目录

矩阵部分

矩阵置零

题目链接：73. 矩阵置零

解题逻辑：

同样要使用原地置0，本题的思想和41. 缺失的第一个正数非常相似，涉及到原地算法的，一个常用的思路就是能不能借助已有的结构完成额外结构需要做的事。

本题我们可以借助于第一行，第一列进行记录是否置0。然后使用两个变量决定最后第一行、第一列是否置0。

解题代码：

java 复制代码 
class Solution {
    public void setZeroes(int[][] matrix) {
        boolean firstRow = false;
        boolean firstCol = false;
        for(int i = 0;i < matrix.length;i++) if(matrix[i][0] == 0) firstCol = true; 
        for(int j = 0;j < matrix[0].length;j++) if(matrix[0][j] == 0) firstRow = true;
        for(int i = 0;i < matrix.length;i++) {
            for(int j = 0;j < matrix[0].length;j++) {
                if(matrix[i][j] == 0) {
                    matrix[i][0] = 0;
                    matrix[0][j] = 0;
                }
            }
        }
        //遍历行置0
        for(int i = 1;i < matrix.length;i++) if(matrix[i][0] == 0) for(int j = 1;j < matrix[0].length;j++) matrix[i][j] = 0;
        //遍历列置0
        for(int j = 1;j < matrix[0].length;j++) if(matrix[0][j] == 0) for(int i = 1;i < matrix.length;i++) matrix[i][j] = 0;
        //将第一列置0
        if(firstCol) for(int i = 0;i < matrix.length;i++) matrix[i][0] = 0;
        //将第一行置0
        if(firstRow) for(int j = 0;j < matrix[0].length;j++) matrix[0][j] = 0;
    }
}

螺旋矩阵

题目链接：54. 螺旋矩阵

解题逻辑：

训练营中已经说到过59. 螺旋矩阵 II，本题的逻辑类似不过多赘述。

解题代码：

java 复制代码 
class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        //(0,1) -> (1,0) -> (0,-1) -> (-1,0)
        int m = matrix.length,n = matrix[0].length;
        int[][] record = new int[m][n];
        int[] dire = {0,1};
        List<Integer> result = new ArrayList<>();
        int[] position = {0,0};
        while(result.size() < m * n) {
            int x = position[0];
            int y = position[1];
            if(record[x][y] == 0) {
                result.add(matrix[x][y]);
                record[x][y] = 1;
            }
            x = x + dire[0];
            y = y + dire[1];
            if(x < 0 || x >= m || y < 0 || y >= n || record[x][y] == 1) {
                int temp = dire[1];
                dire[1] = -dire[0];
                dire[0] = temp;
                x = position[0] + dire[0];
                y = position[1] + dire[1];
            }
            position[0] = x;
            position[1] = y;
        }
        return result;
    }
}

旋转图像

题目链接：48. 旋转图像

解题逻辑：

对于 n x n 的矩阵 matrix，各种对称的转移式如下：

  • 上下对称：matrix[i][j] -> matrix[n-i-1][j]
  • 左右对称：matrix[i][j] -> matrix[i][n-j-1]
  • 主对角线对称：matrix[i][j] -> matrix[j][i]
  • 副对角线对称：matrix[i][j] -> matrix[n-j-1][n-i-1]

这里多次出现的n-i-1以及n-j-1怎么来的？例如上下对称，第i行对称过去相当于从后往前数第i行（最后一行索引是n - 1），也就是n - 1 - i。

然后根据旋转的度数，我们可以根据各种对称的组合来完成，例如：

  • 顺时针 90° 旋转：上下对称 + 主对角线对称 或者 主对角线对称 + 左右对称
  • 顺时针 180° 旋转，可视为两次顺时针 90° 旋转：上下对称 + 左右对称 或者 主对角线对称 + 副对角线对称
  • 顺时针 270°，可以视为顺时针 180° + 顺时针 90°：左右对称 + 主对角线对称

旋转多少度是由哪些对称组合而来，大概画着试一下就出来了，不需要去记忆。但要注意的是组合的前后顺序不能改变。

本题是顺时针旋转90度，使用上下对称 + 主对角线对称 ：

  • 上下对称：matrix[i][j] = matrix[m - 1 - i][j]
  • 主对角线对称：matrix[i][j] = matrix[j][i]

解题代码：

java 复制代码 
class Solution {
    public void rotate(int[][] matrix) {
        int m = matrix.length,n = matrix[0].length;
        //上下对称
        for(int i = 0;i < m / 2;i++) {
            for(int j = 0;j < n;j++) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[m - 1 - i][j];
                matrix[m - 1 - i][j] = temp;
            }
        }
        //主对角线对称
        for(int i = 0;i < m;i++) {
            for(int j = i + 1;j < n;j++) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = temp;
            }
        }
    }
}

搜索二维矩阵

题目链接：240. 搜索二维矩阵 II

解题逻辑：

利用有序性，那么我们可以从两个方向思考：

  • 从小到大寻找，使用二分法
  • 从大到小排除，使用排除法

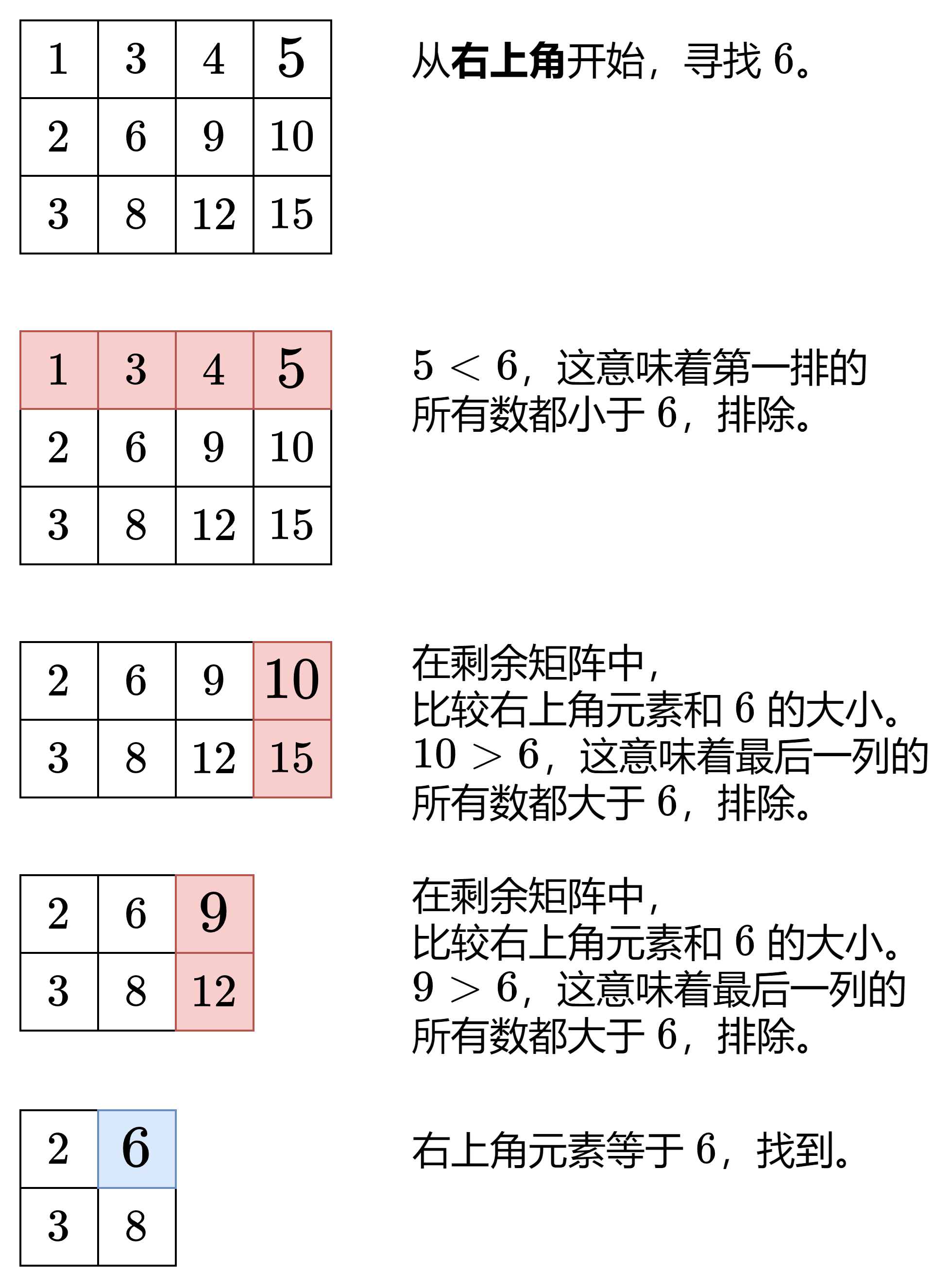
方法1：排除法

从右上角开始，这个数是每一行的最大值，每一列的最小值，以此为根据来进行排除。

图片来源：https://leetcode.cn/problems/search-a-2d-matrix-ii/solutions/2783938/tu-jie-pai-chu-fa-yi-tu-miao-dong-python-kytg/?envType=study-plan-v2\&envId=top-100-liked

java 复制代码 
class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int m = matrix.length,n = matrix[0].length;
        int x = 0,y = n - 1;
        while( y >= 0 && x < m ) {
            int cur = matrix[x][y];
            if(cur == target) return true;
            else if(cur > target) y--;
            else x++;
        }
        return false;
    }
}

方法二：使用二分法，对每行进行搜索

java 复制代码 
class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        for(int[] row : matrix) if(halfSearch(row,target)) return true;
        return false;
    }

    public boolean halfSearch(int[] nums,int target){
        int left = 0;
        int right = nums.length - 1;
        while(left <= right) {
            int middle = (left + right) / 2;
            if(nums[middle] == target) return true;
            else if(nums[middle] > target) right = middle - 1;
            else left = middle + 1;
        }
        return false;
    }
}

堆部分

数组中的第K个最大元素（大顶堆构造）

题目链接：215. 数组中的第K个最大元素

方法一：直接使用Java的集合类

在 Java 的集合框架中，java.util.PriorityQueue 是基于最小堆（默认）实现的类，它提供了堆的核心操作功能。虽然名称中带有 "Queue"，但它本质上是一个堆结构，遵循 "优先级最高的元素先出队" 的规则（默认按自然顺序最小的元素优先级最高）。

代码如下：

java 复制代码 
class Solution {
    public int findKthLargest(int[] nums, int k) {
        Queue<Integer> heap = new PriorityQueue<>((a,b) -> -(a - b));
        for (int num : nums) heap.add(num);
        int result = nums[0];
        for(int i = 0;i < k;i++) result = heap.poll();
        return result;
    }
}

方法二：堆排序 -- 构建一个大根堆

下面将通过Java代码手动实现大顶堆及堆排序，并详细说明实现原理。

大顶堆是一种特殊的完全二叉树，满足以下特性：

  • 每个父节点的值 大于或等于 其左右子节点的值。
  • 通常用数组 存储（完全二叉树的特性可通过索引快速定位父子节点）：
    • 对于索引为 i 的节点：
      • 左子节点索引：2*i + 1
      • 右子节点索引：2*i + 2
      • 父节点索引：(i-1) / 2（整数除法）
  • 最后一个非叶子节点n/2 - 1

大顶堆的核心操作包括：

  1. 堆调整（heapify）：当某个节点违反大顶堆性质时，通过"下沉"操作使其重新满足堆特性。
  2. 构建大顶堆：将无序数组转换为大顶堆。
  3. 堆排序：利用大顶堆的特性（堆顶为最大值）实现排序。
java 复制代码 
public class MaxHeap {

    /**
     * 堆调整（核心操作）：将以i为根的子树调整为大顶堆
     * @param arr 存储堆的数组
     * @param heapSize 当前堆的大小（有效元素范围）
     * @param i 需要调整的节点索引
     */
    public static void heapify(int[] arr, int heapSize, int i) {
        int largest = i; // 初始化最大值为当前节点
        int left = 2 * i + 1; // 左子节点索引
        int right = 2 * i + 2; // 右子节点索引

        // 若左子节点存在且大于当前最大值，更新最大值索引
        if (left < heapSize && arr[left] > arr[largest]) {
            largest = left;
        }

        // 若右子节点存在且大于当前最大值，更新最大值索引
        if (right < heapSize && arr[right] > arr[largest]) {
            largest = right;
        }

        // 若最大值不是当前节点，交换位置并递归调整子树
        if (largest != i) {
            // 交换当前节点与最大值节点
            int temp = arr[i];
            arr[i] = arr[largest];
            arr[largest] = temp;
            // 递归调整被交换的子节点（确保子树仍为大顶堆）
            heapify(arr, heapSize, largest);
        }
    }

    /**
     * 构建大顶堆
     * @param arr 待转换的数组
     */
    public static void buildMaxHeap(int[] arr) {
        int n = arr.length;
        // 从最后一个非叶子节点开始向前调整
        // 最后一个非叶子节点索引：n/2 - 1（叶子节点无需调整）
        for (int i = n / 2 - 1; i >= 0; i--) {
            heapify(arr, n, i);
        }
    }

    /**
     * 堆排序（升序）
     * @param arr 待排序数组
     */
    public static void heapSort(int[] arr) {
        int n = arr.length;

        // 步骤1：将数组构建为大顶堆（此时堆顶为最大值）
        buildMaxHeap(arr);

        // 步骤2：依次提取最大值并调整堆
        for (int i = n - 1; i > 0; i--) {
            // 交换堆顶（最大值）与当前堆的最后一个元素
            int temp = arr[0];
            arr[0] = arr[i];
            arr[i] = temp;

            // 缩小堆的范围（排除已排序的末尾元素），并重新调整堆顶
            heapify(arr, i, 0);
        }
    }

    public static void main(String[] args) {
        int[] arr = {3, 1, 2, 5, 4};
        System.out.println("排序前：");
        for (int num : arr) {
            System.out.print(num + " "); // 输出：3 1 2 5 4
        }

        heapSort(arr);

        System.out.println("\n排序后：");
        for (int num : arr) {
            System.out.print(num + " "); // 输出：1 2 3 4 5
        }
    }
}

实现原理详解

1. 堆调整（heapify）

  • 作用：当某个节点的值小于其子节点时，通过"下沉"操作将其与最大的子节点交换，确保以该节点为根的子树满足大顶堆性质。
  • 过程 ：
    1. 找到当前节点、左子节点、右子节点中的最大值。
    2. 若最大值不是当前节点，交换位置。
    3. 递归调整被交换的子节点（因为交换可能破坏子树的堆结构）。
  • 时间复杂度 ：O(log n)（堆的高度为 log n）。

2. 构建大顶堆

  • 作用：将无序数组转换为大顶堆。
  • 过程 ：
    • 从最后一个非叶子节点 （索引 n/2 - 1）开始，向前依次每个节点执行 heapify 操作。
    • 原因：叶子节点本身就是一个合法的堆，无需调整；从后向前调整可确保每个父节点都大于子节点。
  • 时间复杂度 ：O(n)（而非 O(n log n)，因为底层节点的调整成本更低）。

3. 堆排序

  • 核心思想：利用大顶堆的堆顶是最大值的特性，逐步将最大值放到数组末尾，最终得到升序数组。
  • 步骤 ：
    1. 构建大顶堆（堆顶为最大值）。
    2. 交换堆顶（最大值）与数组末尾元素（此时末尾为最大值）。
    3. 缩小堆的范围（排除已排序的末尾元素），对新堆顶执行 heapify 以恢复大顶堆。
    4. 重复步骤2-3，直到所有元素有序。
  • 时间复杂度 ：O(n log n)（构建堆 O(n) + n-1 次调整 O(log n)）。
  • 空间复杂度 ：O(1)（原地排序，仅需常数额外空间）。

本题的解题代码：

java 复制代码 
class Solution {
    public int findKthLargest(int[] nums, int k) {
        buildMaxHeap(nums);
        for(int i = 1;i < k;i++) {
            int temp = nums[0];
            nums[0] = nums[nums.length - i];
            nums[nums.length - i] = temp;
            maxHeapify(nums,nums.length - i,0);
        }
        return nums[0];
    }

    public static void maxHeapify(int[] nums,int heapSize,int cur){
        //构建大顶堆的调整步骤(当某个节点的值小于其子节点时，通过 "下沉" 操作将其与最大的子节点交换)
        int left = 2 * cur + 1;
        int right = 2 * cur + 2;
        int exchange = cur;
        if(left < heapSize && nums[left] > nums[exchange]) exchange = left;
        if(right < heapSize && nums[right] > nums[exchange]) exchange = right;
        if(exchange != cur) {
            int temp = nums[exchange];
            nums[exchange] = nums[cur];
            nums[cur] = temp;
            maxHeapify(nums,heapSize,exchange);
        }
    }

    public static void buildMaxHeap(int[] nums){
        //从最后一个非叶节点开始，倒序一个个进行调整
        for(int i = nums.length / 2 - 1; i >=0; i--) maxHeapify(nums, nums.length,i);
    }
}

数据流的中位数（对顶堆维护）

题目链接：295. 数据流的中位数

解题逻辑：

计算中位数：

  • 如果数组长度为奇数，则直接返回中间值
  • 如果为偶数，那么我们可以将数组分为两半，而中位数的计算只与前半段的最大值和后半段的最小值有关，所以我们可以用一个大顶堆维护左半部分的数据，使用小顶堆维护右半部分的数据。

那么其实本题的核心就是如何维护这个对顶堆，首先可以明确：

  • 两个堆的大小要尽量相等，我们可以规定奇数个的时候，左堆的个数比右堆多一个。
  • left 的所有元素都应该小于等于 right 的所有元素，也就是说left的堆顶元素一定小于等于right的堆顶元素。

那么为了维护这种关系，一个重要的思想就是堆顶元素的流动，因为只有堆顶元素的流动可以保证left 的所有元素都应该小于等于 right 的所有元素，此处我们可以分情况讨论：

  • 两个堆大小相等的时候，我们可以将该数加入到right堆中，把right堆的堆顶加入到left堆中去，这样一定可以保证left 的所有元素都应该小于等于 right 的所有元素。【堆大小相等，规定的左堆的个数比右堆多一个，所以让堆顶元素向左堆流动】
  • 两个堆大小不相等的时候，按照规定只有可能是left的个数比right多一个，那么此时可以通过将元素加入到left，将left的堆顶加入到right，此时两个堆的大小相等。【堆大小不相等，按照规定，让堆顶元素向右流动，让两堆大小重新相等】

代码如下：

java 复制代码 
class MedianFinder {
    Queue<Integer> left = new PriorityQueue<>((a,b) -> -(a - b));
    Queue<Integer> right = new PriorityQueue<>((a,b) -> a - b);

    public MedianFinder() {
        
    }
    
    public void addNum(int num) {
        if(left.size() == right.size()) {
            right.offer(num);
            left.offer(right.poll());
        }else {
            left.offer(num);
            right.offer(left.poll());
        }
    }
    
    public double findMedian() {
        if(left.size() == right.size()) {
            return ((double)left.peek() + (double)right.peek()) / 2;
        }else {
            return left.peek();   
        }
    }
}

技巧部分

只出现一次的数字（异或运算）

题目链接：136. 只出现一次的数字

解题逻辑：

对于这道题，可使用异或运算 ⊕。异或运算有以下三个性质。

  • 任何数和 0 做异或运算，结果仍然是原来的数，即 a⊕0=a。
  • 任何数和其自身做异或运算，结果是 0，即 a⊕a=0。
  • 异或运算满足交换律和结合律，即 a⊕b⊕a=b⊕a⊕a=b⊕(a⊕a)=b⊕0=b。

根据题目要求只有某一个元素出现一次，其他元素都出现两次，所以通过交换律与结合律，那么将所有的元素异或最后得到的就是只出现一次的那个元素！

总结一下Java中几种常见的位运算符号：

运算符 名称 规则（二进制位） 示例
& 按位与 都为 1 则为 1，否则 0 5 & 3 = 1
| 按位或 至少一个 1 则为 1，否则 0 `5
^ 按位异或 不同则为 1，相同则为 0 5 ^ 3 = 6
~ 按位非 取反（1变0，0变1） ~5 = -6
<< 左移 左移 n 位，低位补 0 5 << 2 = 20
>> 算术右移 右移 n 位，高位补符号位 5 >> 2 = 1
>>> 无符号右移 右移 n 位，高位补 0 -5 >>> 2 = 1073741822

解题代码：

java 复制代码 
class Solution {
    public int singleNumber(int[] nums) {
        int result = 0;
        for(int num : nums) result ^= num;
        return result;
    }
}

多数元素（摩尔投票）

题目链接：169. 多数元素

解题逻辑：

摩尔投票算法（Boyer-Moore Majority Vote Algorithm）是一种高效的找出众数查找算法，用于在无序数组中快速找到出现次数超过数组长度 1/k 的元素（最经典的是找出现次数超过 1/2 的元素）。其核心优势是时间复杂度 O (n)、空间复杂度 O (1)，无需额外存储大量元素计数。

核心原理

摩尔投票算法的核心思想是 "抵消"：通过不断消除不同元素，最终剩下的元素可能是要找的多数元素（需最后验证）。

解题代码：

java 复制代码 
class Solution {
    public int majorityElement(int[] nums) {
        int counter = 1;
        int cur = nums[0];
        if(nums.length == 1) return nums[0];
        for(int i = 1;i < nums.length;i++) {
            if(cur == nums[i]) counter++;
            else {
                if(counter == 0) {
                    cur = nums[i];
                    counter = 1;
                }
                counter--;
            }
        }
        return cur;
    }
}

拓展：如果查找出现次数超过 1/k 的元素怎么办？

根据摩尔投票算法的扩展原理，最多有 k-1 个元素满足出现次数超过 1/k，因此需要维护 k-1 个候选元素及其计数器。

实现思路

  1. 初始化 ：创建两个数组，分别存储 k-1 个候选元素（candidates）和对应的计数（counts）。
  2. 投票阶段 ：遍历数组元素，对每个元素：
    • 若与某个候选元素相同，则对应计数器加 1。
    • 若不存在相同候选，且有计数器为 0，则替换该候选元素并将计数器设为 1。
    • 若既无相同候选，也无空计数器，则所有计数器减 1（抵消）。
  3. 验证阶段 ：统计每个候选元素的实际出现次数，筛选出超过 n/k 的元素（n 为数组长度）。

代码实现

java 复制代码 
import java.util.ArrayList;
import java.util.List;

public class FindElementsMoreThan1OverK {

    /**
     * 查找数组中出现次数超过 1/k 的所有元素
     * @param nums 输入数组
     * @param k 比例分母
     * @return 满足条件的元素列表
     */
    public static List<Integer> findElements(int[] nums, int k) {
        List<Integer> result = new ArrayList<>();
        if (nums == null || nums.length == 0 || k <= 1) {
            // k<=1 时，所有元素都满足（1/k >=1），直接返回去重后结果
            for (int num : nums) {
                if (!result.contains(num)) {
                    result.add(num);
                }
            }
            return result;
        }

        int n = nums.length;
        int m = k - 1; // 最多 m 个候选元素
        int[] candidates = new int[m]; // 存储候选元素
        int[] counts = new int[m];     // 存储对应候选的计数

        // 投票阶段：筛选候选元素
        for (int num : nums) {
            boolean found = false;
            // 1. 检查是否与已有候选匹配
            for (int i = 0; i < m; i++) {
                if (counts[i] > 0 && candidates[i] == num) {
                    counts[i]++;
                    found = true;
                    break;
                }
            }
            if (found) continue;

            // 2. 若不匹配，检查是否有计数为0的候选位置（可替换）
            for (int i = 0; i < m; i++) {
                if (counts[i] == 0) {
                    candidates[i] = num;
                    counts[i] = 1;
                    found = true;
                    break;
                }
            }
            if (found) continue;

            // 3. 若既不匹配也无空位置，所有计数减1（抵消）
            for (int i = 0; i < m; i++) {
                counts[i]--;
            }
        }

        // 验证阶段：统计候选元素的实际出现次数，判断是否超过 n/k
        for (int i = 0; i < m; i++) {
            if (counts[i] == 0) continue; // 跳过无效候选
            int actualCount = 0;
            for (int num : nums) {
                if (num == candidates[i]) {
                    actualCount++;
                }
            }
            if (actualCount > n / k) {
                result.add(candidates[i]);
            }
        }

        return result;
    }

    public static void main(String[] args) {
        // 测试用例1：查找出现次数超过 1/3 的元素（最多2个）
        int[] nums1 = {3, 2, 3, 1, 1, 2, 1};
        System.out.println("超过 1/3 的元素：" + findElements(nums1, 3)); // 输出 [1]

        // 测试用例2：查找出现次数超过 1/2 的元素（最多1个）
        int[] nums2 = {2, 2, 1, 1, 1, 2, 2};
        System.out.println("超过 1/2 的元素：" + findElements(nums2, 2)); // 输出 [2]

        // 测试用例3：查找出现次数超过 1/4 的元素（最多3个）
        int[] nums3 = {4, 3, 4, 2, 4, 2, 2, 4};
        System.out.println("超过 1/4 的元素：" + findElements(nums3, 4)); // 输出 [4, 2]
    }
}

颜色分类（荷兰国旗问题）

题目链接：75. 颜色分类

解题逻辑：

此题的本质是通过三指针（两个边界指针left、right，一个遍历指针i）维护三个区间，left指向下一个交换0的位置，right指向下一个交换1的位置。所以可以确定：

  • 0,left − 1\] 均为 0

  • 由于 [0,i − 1] 均为处理过的数值（即 0 和 2 必然都被分到了两端），同时 left − 1 又是 0 的右边界。所以
  • [left,i − 1] 均为1,也就是说如果没有1，left和i应该一直是一样的，如果有1两者才会分开
  • [i,right] 为未处理的数值

那么指针的运动规则如下：

  • i指向的元素为0，则与left指针进行交换，然后left指针右移，由于【left，i- 1】之间维护的是1，那么left交换过来的一定是1，所以i也要右移
  • i指向的元素为1，则i直接右移
  • i指向的元素为2，则与right指针进行交换，然后right指针左移，由于交换过来的元素不知道大小，所以i维持不变进入下一次循环继续判断

题目代码：

java 复制代码 
class Solution {
    public void sortColors(int[] nums) {
        int left = 0;
        int right = nums.length - 1;
        int i = 0;
        while(i <= right && left <= right) {
            if(nums[i] == 0) swap(nums,left++,i++);    
            else if(nums[i] == 2) swap(nums,right--,i);
            else i++;
        }
    }

    public void swap(int[] nums,int left,int right){
        int temp = nums[left];
        nums[left] = nums[right];
        nums[right] = temp;
    }
}

下一个排列

题目链接：31. 下一个排列

解题逻辑：

leetcode中的一个题解写的非常的清晰：下一个排列算法详解：思路+推导+步骤，看不懂算我输！

解题代码：

java 复制代码 
class Solution {
    public void nextPermutation(int[] nums) {
        if(nums.length < 2) return;
        int left = nums.length - 2;
        int right = nums.length - 1;
        while(left > 0 && nums[left] >= nums[right]) {
            left--;
            right--;
        }
        if(nums[left] >= nums[right]) {
            Arrays.sort(nums);
            return;
        }
        int smallerBigNum = right;
        while(right < nums.length) {
            if(nums[right] < nums[smallerBigNum] && nums[right] > nums[left]) smallerBigNum = right;
            right++;
        }
        swap(nums,left,smallerBigNum);
        Arrays.sort(nums,left + 1,nums.length);
    }

    public void swap(int[] nums,int left,int right){
        int temp = nums[left];
        nums[left] = nums[right];
        nums[right] = temp;
    }

}

寻找重复数

题目链接：287. 寻找重复数

解题逻辑：

这一题可以使用在环形链表 II中使用过的快慢指针思想。

也就是说我们可以将这个数组转换成为链表，而找到重复的数字也就是找到环的入口。那么本题的重点就在于怎么将这个数组转换成为链表。

注意到题目说：给定一个包含 n + 1 个整数的数组 nums ，其数字都在 [1, n] 范围内（包括 1 和 n），可知至少存在一个重复的整数。所以我们可以从nums[0]作为头节点，接下来将nums[0]索引处的元素作为下一个节点，然后将nums[nums[0]]索引处的元素作为再下一个元素，以此类推。相当于使用数组元素作为索引，将整个数组串联成链表。

解题代码：

java 复制代码 
class Solution {
    public int findDuplicate(int[] nums) {
        int fast = nums[0];
        int slow = nums[0];
        while(fast < nums.length && nums[fast] < nums.length) {
            fast = nums[nums[fast]];
            slow = nums[slow];
            if(fast == slow) {
                slow = nums[0];
                while(fast != slow) {
                    fast = nums[fast];
                    slow = nums[slow];
                }
                return fast;
            }
        }
        return -1;
    }
}
相关推荐
一路往蓝-Anbo2 小时前
C语言从句柄到对象 (三) —— 抛弃 Malloc：静态对象池与索引句柄的终极形态
c语言·开发语言·数据结构·stm32·单片机·算法
fantasy_arch2 小时前
SVT-AV1 B帧决策和mini-GOP决策分析
算法·av1
声声codeGrandMaster2 小时前
逻辑回归-泰坦尼克号
算法·机器学习·逻辑回归
mu_guang_3 小时前
算法图解2-选择排序
数据结构·算法·排序算法
xiaowu0803 小时前
IEnumerable、IEnumerator接口与yield return关键字的相关知识
java·开发语言·算法
报错小能手3 小时前
数据结构 b+树
数据结构·b树·算法
POLITE33 小时前
Leetcode 238.除了自身以外数组的乘积 JavaScript (Day 7)
前端·javascript·leetcode
元亓亓亓3 小时前
LeetCode热题100--64. 最小路径和--中等
算法·leetcode·职场和发展
热门推荐
01GitHub 镜像站点02从快手“12·22”直播攻击事件看：一次教科书式的业务层饱和攻击03Claude Code Skills 实用使用手册04Linux下V2Ray安装配置指南05jdk21下载、安装（Windows、Linux、macOS）06UV安装并设置国内源07电脑检测软件—图吧工具箱082025 最新教程：注册并切换到美区 Apple ID09Google Antigravity Agent 编辑器操作教程10【踩坑笔记】50系显卡适配的 PyTorch 安装