KNN算法基础 机器学习基础1 python人工智能

上一篇：机器学习简介 扫盲版 机器学习基础0 python人工智能

目录

简介

数学基础

[1. 欧氏距离（Euclidean Distance）](#1. 欧氏距离（Euclidean Distance）)

[2. 曼哈顿距离（Manhattan Distance）](#2. 曼哈顿距离（Manhattan Distance）)

[3. 切比雪夫距离（Chebyshev Distance）](#3. 切比雪夫距离（Chebyshev Distance）)

[4. 闵氏距离（Minkowski Distance）](#4. 闵氏距离（Minkowski Distance）)

分类思想

回归思想

特征值预处理

归一化

标准化

案例：鸢尾花

dm01_load_iris()输出：

dm02_show_iris()输出：

dm03_split_train_test()输出：

dm04_iris_evaluate_test()输出：

简介

K 近邻（K-Nearest Neighbor，KNN）是一种基于 "相似样本具有相似标签"的简单机器学习算法，既可以做分类也能做回归。核心逻辑是：对新样本，计算它与训练集中所有样本的距离，取距离最近的 K 个样本（"邻居"），用这 K 个样本的标签来推断新样本的结果。

数学基础

KNN 通过 "计算样本间距离" 找邻居，常用这 4 种距离：

1. 欧氏距离（Euclidean Distance）

最常用的 "直线距离"，适合数值型特征：

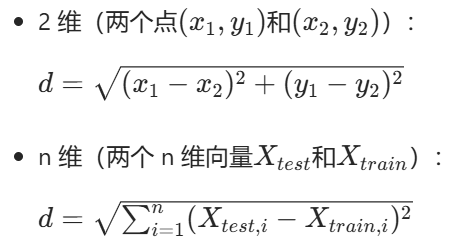
2. 曼哈顿距离（Manhattan Distance）

也叫 "城市街区距离"，模拟 "水平 + 垂直" 的移动路径：

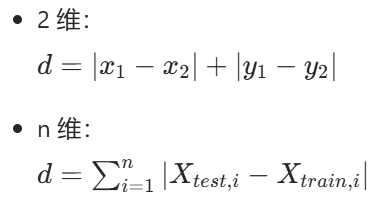
3. 切比雪夫距离（Chebyshev Distance）

模拟 "国际象棋中王的移动"（走最少步数），取各维度差的最大值：

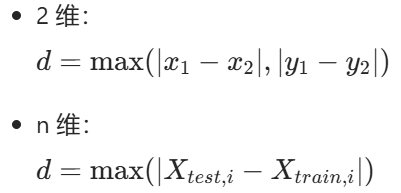
4. 闵氏距离（Minkowski Distance）

前 3 种距离的 "统一形式"，由参数p控制：

分类思想

KNN 分类的核心是"少数服从多数"，步骤如下：

1. 计算新样本（X_test）与所有训练样本（X_train）的距离（常用欧氏距离）；
2. 对距离排序，选取最近的 K 个训练样本；
3. 统计这 K 个样本中出现次数最多的标签，作为新样本的预测分类。

K 值选择技巧：

• K 太小：模型易过拟合（对噪声敏感）；
• K 太大：模型欠拟合（忽略局部特征）；
• 常用交叉验证、网格搜索确定最优 K（比如 K=√样本数）。

# 1. 导包.
from sklearn.neighbors import KNeighborsClassifier # 分类
# from sklearn.neighbors import KNeighborsRegressor # 回归

# 2. 准备数据集(测试集 和 训练集)
# train: 训练集
# test: 测试集
# neighbors: 最近邻的邻居数
x_train = [[0], [1], [2], [3]]  # 训练集的特征数据, 因为特征可以有多个特征, 所以是一个二维数组
y_train = [0, 0, 1, 1]  # 训练集的标签数据, 因为标签是离散的, 所以是一个一维数组
x_test = [[5]]  # 测试集的特征数据

# 3. 创建(KNN 分类模型)模型对象.
estimator=KNeighborsClassifier(n_neighbors=3)

# 4. 模型训练.
# 传入: 训练集的特征数据, 训练集的标签数据
estimator.fit(x_train, y_train)

# 5. 模型预测.
# 传入: 测试集的特征数据, 获取到: 预测结果(测试集的标签, y_test)
y_test=estimator.predict(x_test)

# 6. 打印预测结果.
print(f'预测值为: {y_test}') # 预测值为: [1]

回归思想

KNN 回归的逻辑与分类类似，区别是用 "平均值" 代替 "多数投票"：

1. 同样计算新样本与训练样本的距离，选最近的 K 个邻居；
2. 取这 K 个邻居的标签平均值，作为新样本的预测值。

# 1. 导包
from sklearn.neighbors import KNeighborsRegressor

# 2. 准备数据集
x_train=[[0, 0, 1], [1, 1, 0], [3, 10, 10], [4, 11, 12]]
y_train=[0.1, 0.2, 0.3, 0.4]
x_test=[[3, 11, 10]]

# 3. 创建模型对象
estimator=KNeighborsRegressor(n_neighbors=2)

# 4. 模型训练
estimator.fit(x_train, y_train)

# 5. 模型预测
y_test=estimator.predict(x_test)

# 6. 预测结果
print(f'预测值为: {y_test}')

特征值预处理

特征的单位 / 数值范围差异会 "干扰距离计算"（比如 "身高（米）" 和 "体重（千克）" 的数值差异会让体重主导距离），因此需要先对特征做预处理。

归一化

归一化是将特征映射到指定区间（默认 0,1），公式为：

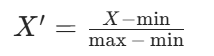
*示例：*原数据：\[90,2, 60,4, 75,3]

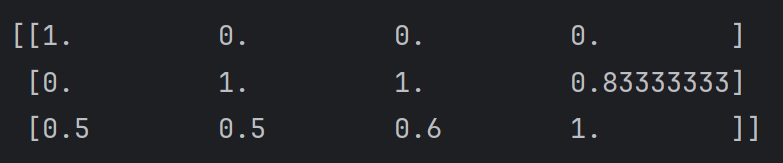
• 第一列（90、60、75）：min=60，max=90 → 映射后：(90-60)/30=1，(60-60)/30=0，(75-60)/30=0.5
• 第二列（2、4、3）：min=2，max=4 → 映射后：0、1、0.5最终归一化结果：\[1,0, 0,1, 0.5,0.5]

# 归一化的步骤：
from sklearn.preprocessing import MinMaxScaler,StandardScaler # 归一化对象

# 1. 准备数据集(归一化之前的原数据).
x_train = [[90, 2, 10, 40], [60, 4, 15, 45], [75, 3, 13, 46]]

# 2. 创建归一化对象.
# 参数feature_range 表示生成范围, 默认为: 0, 1  如果就是这个区间, 则参数可以省略不写.
transfer = MinMaxScaler()
# transfer = MinMaxScaler(feature_range=(3,5))

# 3. 对原数据集进行归一化操作.
x_train_new=transfer.fit_transform(x_train)

# 4. 打印处理后的数据.
print('归一化后的数据集为: \n')
print(x_train_new)

输出：

标准化

标准化是将特征转换为均值 = 0、方差 = 1 的正态分布，公式为：

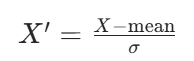
（其中 mean 是特征均值，σ 是特征标准差）

适用场景： 数据分布较分散、存在极端值的情况（比如身高数据中包含异常值）。

# 1. 准备数据集
x_train = [[90, 2, 10, 40], [60, 4, 15, 45], [75, 3, 13, 46]]

# 2. 创建标准化对象.
transfer = StandardScaler()

# 3. 对原数据集进行标准化操作.
x_train_new = transfer.fit_transform(x_train)

# 4. 打印处理后的数据.
print('标准化后的数据集为: \n')
print(x_train_new)

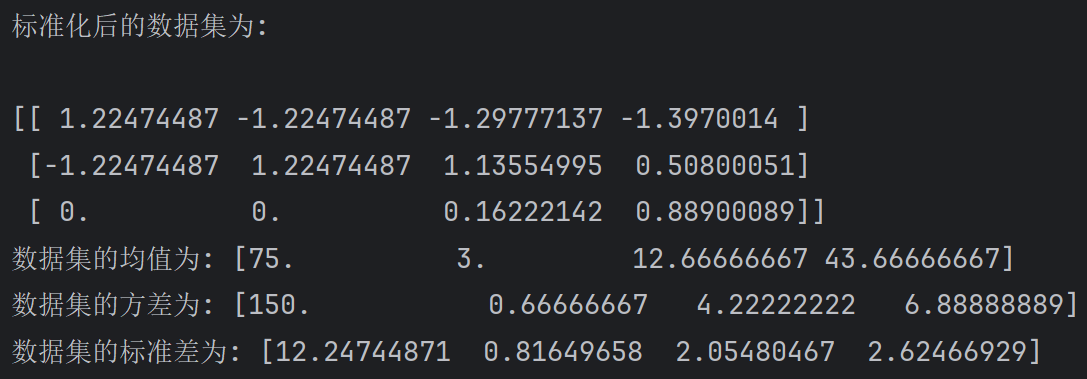
# 5. 打印数据集的均值和方差.
print(f'数据集的均值为: {transfer.mean_}')
print(f'数据集的方差为: {transfer.var_}')
print(f'数据集的标准差为: {transfer.scale_}')

输出：

案例：鸢尾花

# 导包
from sklearn.datasets import load_iris # 加载鸢尾花测试集的.
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split # 分割训练集和测试集
from sklearn.metrics import accuracy_score  # 模型评估的, 计算模型预测的准确率
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

# 加载鸢尾花数据集，并查看数据
def dm01_load_iris():
    # 加载鸢尾花数据集.
    iris_data=load_iris()

    # print(f'数据集：{iris_data}')  # 字典
    print(f'所有的键：{iris_data.keys()}') # ['data', 'target', 'target_names', 'DESCR', 'feature_names', 'filename']
    print(f'具体数据：{iris_data.data}')
    print(f'标签：{iris_data.target}')
    print(f'标签对应的名称：{iris_data.target_names}')
    print(f'特征对应的名称：{iris_data.feature_names}')

# 绘制数据集的散点图
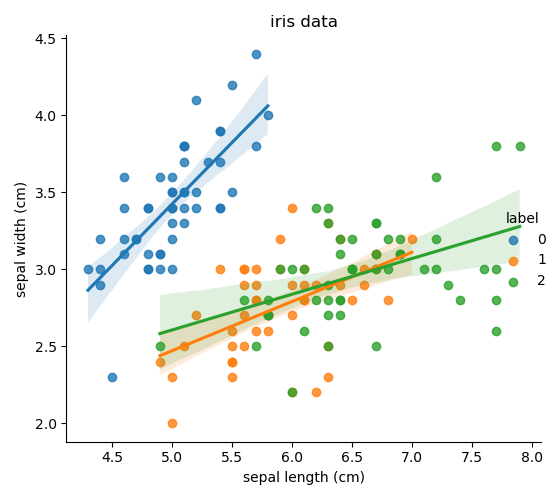
def dm02_show_iris():
    # 加载数据集.
    iris_data = load_iris()
    # 把 鸢尾花数据集封装成 DataFrame对象.
    iris_df=pd.DataFrame(iris_data.data, columns=iris_data.feature_names)
    # print(f'iris_df:\n{iris_df}')
    # 给df对象新增1列 -> 标签列.
    iris_df['label']=iris_data.target
    # print(iris_df)

    # 通过 Seaborn绘制散点图.
    # 参1: 数据集. 参2: x轴. 参3: y轴. 参4: 分组字段. 参5: 是否显示拟合线.
    sns.lmplot(data=iris_df, x='sepal length (cm)', y='sepal width (cm)', hue='label', fit_reg=True)
    # 设置标题, 显式.
    plt.title('iris data')
    plt.tight_layout() # 自动调整子图参数, 以使整个图像的边界与子图匹配.
    plt.show()

# 切分训练集和测试集
def dm03_split_train_test():
    # 加载数据集.
    iris_data = load_iris()

    # 数据的预处理: 从150个特征和标签中, 按照 8:2的比例, 切分训练集和测试集.
    # 参1: 特征数据. 参2: 标签数据. 参3: 测试集的比例.  参4: 随机种子(种子一致, 每次生成的随机数据集都是固定的)
    # 返回值: 训练集的特征数据, 测试集的特征数据, 训练集的标签数据, 测试集的标签数据.
    x_train, x_test, y_train, y_test = train_test_split(iris_data.data, iris_data.target, test_size=0.2, random_state=23)

    # 打印切割后的结果.
    print(f'训练集的特征: {x_train}, 个数: {len(x_train)}')
    print(f'训练集的标签: {y_train}, 个数: {len(y_train)}')
    print(f'测试集的特征: {x_test}, 个数: {len(x_test)}')
    print(f'测试集的标签: {y_test}, 个数: {len(y_test)}')

# 定义函数, 实现鸢尾花完整案例 -> 加载数据, 数据预处理, 特征工程, 模型训练, 模型评估, 模型预测.
def dm04_iris_evaluate_test():
    # 加载数据集.
    iris_data = load_iris()
    # 拆分训练集和测试集.
    x_train, x_test, y_train, y_test = train_test_split(iris_data.data, iris_data.target, test_size=0.2, random_state=23)

    # 特征工程(提取, 预处理...)
    # 标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)

    # 模型训练.
    estimator = KNeighborsClassifier(n_neighbors=3)
    estimator.fit(x_train, y_train)

    # 模型预测.
    y_pre = estimator.predict(x_test)
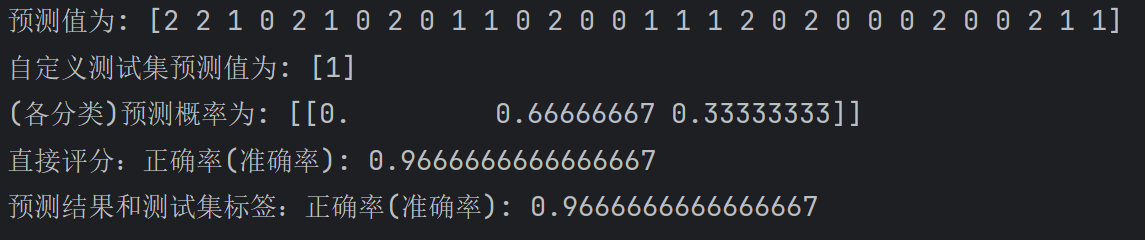
    print(f'预测值为: {y_pre}')

    # 自定义的测试数据
    my_data = [[7.8, 2.1, 3.9, 1.6]]
    # 标准化
    my_data = transfer.transform(my_data)
    # 模型预测.
    y_pre_new = estimator.predict(my_data)
    print(f'自定义测试集预测值为: {y_pre_new}')

    # 5.4 查看上述数据集, 每种分类的预测概率.
    y_pre_proba = estimator.predict_proba(my_data)
    print(f'(各分类)预测概率为: {y_pre_proba}')  # [[0, 0.66666667, 0.33333333]] -> 0分类的概率, 1分类的概率, 2分类的概率.

    # 模型评估.
    # 方式1: 直接评分, 基于: 测试集的特征 和 测试集集的标签.
    print(f'直接评分：正确率(准确率): {estimator.score(x_test, y_test)}')  # 0.9666666666666667
    # 方式2: 基于 测试集的标签 和 预测结果 进行评分.
    print(f'预测结果和测试集标签：正确率(准确率): {accuracy_score(y_test, y_pre)}')  # 0.9666666666666667


# 测试
if __name__ == '__main__':
    # dm01_load_iris()
    # dm02_show_iris()
    # dm03_split_train_test()
    dm04_iris_evaluate_test()

dm01_load_iris()输出：

太长了不好截图，这里复制过来折叠一下

所有的键：dict_keys(['data', 'target', 'frame', 'target_names', 'DESCR', 'feature_names', 'filename', 'data_module'])
具体数据：[[5.1 3.5 1.4 0.2]
 [4.9 3.  1.4 0.2]
 [4.7 3.2 1.3 0.2]
 [4.6 3.1 1.5 0.2]
 [5.  3.6 1.4 0.2]
 [5.4 3.9 1.7 0.4]
 [4.6 3.4 1.4 0.3]
 [5.  3.4 1.5 0.2]
 [4.4 2.9 1.4 0.2]
 [4.9 3.1 1.5 0.1]
 [5.4 3.7 1.5 0.2]
 [4.8 3.4 1.6 0.2]
 [4.8 3.  1.4 0.1]
 [4.3 3.  1.1 0.1]
 [5.8 4.  1.2 0.2]
 [5.7 4.4 1.5 0.4]
 [5.4 3.9 1.3 0.4]
 [5.1 3.5 1.4 0.3]
 [5.7 3.8 1.7 0.3]
 [5.1 3.8 1.5 0.3]
 [5.4 3.4 1.7 0.2]
 [5.1 3.7 1.5 0.4]
 [4.6 3.6 1.  0.2]
 [5.1 3.3 1.7 0.5]
 [4.8 3.4 1.9 0.2]
 [5.  3.  1.6 0.2]
 [5.  3.4 1.6 0.4]
 [5.2 3.5 1.5 0.2]
 [5.2 3.4 1.4 0.2]
 [4.7 3.2 1.6 0.2]
 [4.8 3.1 1.6 0.2]
 [5.4 3.4 1.5 0.4]
 [5.2 4.1 1.5 0.1]
 [5.5 4.2 1.4 0.2]
 [4.9 3.1 1.5 0.2]
 [5.  3.2 1.2 0.2]
 [5.5 3.5 1.3 0.2]
 [4.9 3.6 1.4 0.1]
 [4.4 3.  1.3 0.2]
 [5.1 3.4 1.5 0.2]
 [5.  3.5 1.3 0.3]
 [4.5 2.3 1.3 0.3]
 [4.4 3.2 1.3 0.2]
 [5.  3.5 1.6 0.6]
 [5.1 3.8 1.9 0.4]
 [4.8 3.  1.4 0.3]
 [5.1 3.8 1.6 0.2]
 [4.6 3.2 1.4 0.2]
 [5.3 3.7 1.5 0.2]
 [5.  3.3 1.4 0.2]
 [7.  3.2 4.7 1.4]
 [6.4 3.2 4.5 1.5]
 [6.9 3.1 4.9 1.5]
 [5.5 2.3 4.  1.3]
 [6.5 2.8 4.6 1.5]
 [5.7 2.8 4.5 1.3]
 [6.3 3.3 4.7 1.6]
 [4.9 2.4 3.3 1. ]
 [6.6 2.9 4.6 1.3]
 [5.2 2.7 3.9 1.4]
 [5.  2.  3.5 1. ]
 [5.9 3.  4.2 1.5]
 [6.  2.2 4.  1. ]
 [6.1 2.9 4.7 1.4]
 [5.6 2.9 3.6 1.3]
 [6.7 3.1 4.4 1.4]
 [5.6 3.  4.5 1.5]
 [5.8 2.7 4.1 1. ]
 [6.2 2.2 4.5 1.5]
 [5.6 2.5 3.9 1.1]
 [5.9 3.2 4.8 1.8]
 [6.1 2.8 4.  1.3]
 [6.3 2.5 4.9 1.5]
 [6.1 2.8 4.7 1.2]
 [6.4 2.9 4.3 1.3]
 [6.6 3.  4.4 1.4]
 [6.8 2.8 4.8 1.4]
 [6.7 3.  5.  1.7]
 [6.  2.9 4.5 1.5]
 [5.7 2.6 3.5 1. ]
 [5.5 2.4 3.8 1.1]
 [5.5 2.4 3.7 1. ]
 [5.8 2.7 3.9 1.2]
 [6.  2.7 5.1 1.6]
 [5.4 3.  4.5 1.5]
 [6.  3.4 4.5 1.6]
 [6.7 3.1 4.7 1.5]
 [6.3 2.3 4.4 1.3]
 [5.6 3.  4.1 1.3]
 [5.5 2.5 4.  1.3]
 [5.5 2.6 4.4 1.2]
 [6.1 3.  4.6 1.4]
 [5.8 2.6 4.  1.2]
 [5.  2.3 3.3 1. ]
 [5.6 2.7 4.2 1.3]
 [5.7 3.  4.2 1.2]
 [5.7 2.9 4.2 1.3]
 [6.2 2.9 4.3 1.3]
 [5.1 2.5 3.  1.1]
 [5.7 2.8 4.1 1.3]
 [6.3 3.3 6.  2.5]
 [5.8 2.7 5.1 1.9]
 [7.1 3.  5.9 2.1]
 [6.3 2.9 5.6 1.8]
 [6.5 3.  5.8 2.2]
 [7.6 3.  6.6 2.1]
 [4.9 2.5 4.5 1.7]
 [7.3 2.9 6.3 1.8]
 [6.7 2.5 5.8 1.8]
 [7.2 3.6 6.1 2.5]
 [6.5 3.2 5.1 2. ]
 [6.4 2.7 5.3 1.9]
 [6.8 3.  5.5 2.1]
 [5.7 2.5 5.  2. ]
 [5.8 2.8 5.1 2.4]
 [6.4 3.2 5.3 2.3]
 [6.5 3.  5.5 1.8]
 [7.7 3.8 6.7 2.2]
 [7.7 2.6 6.9 2.3]
 [6.  2.2 5.  1.5]
 [6.9 3.2 5.7 2.3]
 [5.6 2.8 4.9 2. ]
 [7.7 2.8 6.7 2. ]
 [6.3 2.7 4.9 1.8]
 [6.7 3.3 5.7 2.1]
 [7.2 3.2 6.  1.8]
 [6.2 2.8 4.8 1.8]
 [6.1 3.  4.9 1.8]
 [6.4 2.8 5.6 2.1]
 [7.2 3.  5.8 1.6]
 [7.4 2.8 6.1 1.9]
 [7.9 3.8 6.4 2. ]
 [6.4 2.8 5.6 2.2]
 [6.3 2.8 5.1 1.5]
 [6.1 2.6 5.6 1.4]
 [7.7 3.  6.1 2.3]
 [6.3 3.4 5.6 2.4]
 [6.4 3.1 5.5 1.8]
 [6.  3.  4.8 1.8]
 [6.9 3.1 5.4 2.1]
 [6.7 3.1 5.6 2.4]
 [6.9 3.1 5.1 2.3]
 [5.8 2.7 5.1 1.9]
 [6.8 3.2 5.9 2.3]
 [6.7 3.3 5.7 2.5]
 [6.7 3.  5.2 2.3]
 [6.3 2.5 5.  1.9]
 [6.5 3.  5.2 2. ]
 [6.2 3.4 5.4 2.3]
 [5.9 3.  5.1 1.8]]
标签：[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2]
标签对应的名称：['setosa' 'versicolor' 'virginica']
特征对应的名称：['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']

dm02_show_iris()输出：

dm03_split_train_test()输出：

太长了不好截图，这里复制过来折叠一下

训练集的特征: [[4.9 3.1 1.5 0.1]
 [5.2 2.7 3.9 1.4]
 [5.4 3.9 1.3 0.4]
 [7.7 2.8 6.7 2. ]
 [5.  3.4 1.5 0.2]
 [5.4 3.9 1.7 0.4]
 [6.5 2.8 4.6 1.5]
 [5.  2.3 3.3 1. ]
 [5.7 3.  4.2 1.2]
 [6.3 3.3 6.  2.5]
 [6.9 3.2 5.7 2.3]
 [4.8 3.4 1.9 0.2]
 [5.5 2.4 3.7 1. ]
 [4.6 3.2 1.4 0.2]
 [6.3 2.3 4.4 1.3]
 [6.3 2.5 5.  1.9]
 [4.9 2.5 4.5 1.7]
 [7.9 3.8 6.4 2. ]
 [4.9 3.1 1.5 0.2]
 [5.7 2.8 4.1 1.3]
 [7.4 2.8 6.1 1.9]
 [6.2 3.4 5.4 2.3]
 [5.5 4.2 1.4 0.2]
 [6.1 2.6 5.6 1.4]
 [5.4 3.  4.5 1.5]
 [7.  3.2 4.7 1.4]
 [7.7 3.8 6.7 2.2]
 [5.9 3.  4.2 1.5]
 [5.  3.6 1.4 0.2]
 [6.5 3.2 5.1 2. ]
 [6.7 3.  5.  1.7]
 [4.7 3.2 1.6 0.2]
 [5.8 2.6 4.  1.2]
 [5.1 3.3 1.7 0.5]
 [6.4 2.8 5.6 2.1]
 [5.5 2.3 4.  1.3]
 [6.8 2.8 4.8 1.4]
 [6.4 2.8 5.6 2.2]
 [5.8 2.8 5.1 2.4]
 [6.3 2.5 4.9 1.5]
 [4.9 3.6 1.4 0.1]
 [5.  3.4 1.6 0.4]
 [6.3 3.4 5.6 2.4]
 [4.9 3.  1.4 0.2]
 [4.8 3.4 1.6 0.2]
 [6.8 3.  5.5 2.1]
 [5.8 2.7 5.1 1.9]
 [5.5 2.5 4.  1.3]
 [4.4 2.9 1.4 0.2]
 [5.6 3.  4.1 1.3]
 [6.4 2.7 5.3 1.9]
 [6.2 2.2 4.5 1.5]
 [6.5 3.  5.8 2.2]
 [7.6 3.  6.6 2.1]
 [6.2 2.9 4.3 1.3]
 [4.4 3.2 1.3 0.2]
 [6.1 2.8 4.  1.3]
 [5.6 2.8 4.9 2. ]
 [6.1 3.  4.9 1.8]
 [6.  2.2 4.  1. ]
 [5.2 3.5 1.5 0.2]
 [5.7 2.8 4.5 1.3]
 [6.  3.4 4.5 1.6]
 [5.8 2.7 3.9 1.2]
 [6.  2.2 5.  1.5]
 [5.9 3.2 4.8 1.8]
 [5.5 2.4 3.8 1.1]
 [5.8 2.7 5.1 1.9]
 [7.3 2.9 6.3 1.8]
 [7.2 3.6 6.1 2.5]
 [5.8 4.  1.2 0.2]
 [6.7 3.3 5.7 2.1]
 [5.1 2.5 3.  1.1]
 [5.2 4.1 1.5 0.1]
 [6.8 3.2 5.9 2.3]
 [6.  3.  4.8 1.8]
 [5.1 3.5 1.4 0.2]
 [6.  2.9 4.5 1.5]
 [5.6 2.7 4.2 1.3]
 [6.5 3.  5.2 2. ]
 [4.4 3.  1.3 0.2]
 [4.6 3.6 1.  0.2]
 [5.  2.  3.5 1. ]
 [4.3 3.  1.1 0.1]
 [6.3 3.3 4.7 1.6]
 [5.7 2.9 4.2 1.3]
 [5.  3.2 1.2 0.2]
 [6.7 2.5 5.8 1.8]
 [6.4 2.9 4.3 1.3]
 [5.6 3.  4.5 1.5]
 [5.  3.  1.6 0.2]
 [7.7 2.6 6.9 2.3]
 [6.6 2.9 4.6 1.3]
 [5.9 3.  5.1 1.8]
 [6.3 2.9 5.6 1.8]
 [6.7 3.1 4.7 1.5]
 [5.7 4.4 1.5 0.4]
 [5.  3.5 1.6 0.6]
 [6.5 3.  5.5 1.8]
 [7.2 3.  5.8 1.6]
 [6.7 3.1 4.4 1.4]
 [5.5 3.5 1.3 0.2]
 [6.7 3.  5.2 2.3]
 [4.9 2.4 3.3 1. ]
 [6.7 3.3 5.7 2.5]
 [5.7 2.6 3.5 1. ]
 [4.5 2.3 1.3 0.3]
 [5.3 3.7 1.5 0.2]
 [5.1 3.7 1.5 0.4]
 [6.9 3.1 5.1 2.3]
 [5.  3.3 1.4 0.2]
 [4.8 3.  1.4 0.1]
 [6.3 2.7 4.9 1.8]
 [4.6 3.4 1.4 0.3]
 [5.5 2.6 4.4 1.2]
 [5.1 3.4 1.5 0.2]
 [6.1 3.  4.6 1.4]
 [5.4 3.4 1.5 0.4]
 [5.  3.5 1.3 0.3]
 [6.  2.7 5.1 1.6]], 个数: 120
训练集的标签: [0 1 0 2 0 0 1 1 1 2 2 0 1 0 1 2 2 2 0 1 2 2 0 2 1 1 2 1 0 2 1 0 1 0 2 1 1
 2 2 1 0 0 2 0 0 2 2 1 0 1 2 1 2 2 1 0 1 2 2 1 0 1 1 1 2 1 1 2 2 2 0 2 1 0
 2 2 0 1 1 2 0 0 1 0 1 1 0 2 1 1 0 2 1 2 2 1 0 0 2 2 1 0 2 1 2 1 0 0 0 2 0
 0 2 0 1 0 1 0 0 1], 个数: 120
测试集的特征: [[6.9 3.1 5.4 2.1]
 [7.2 3.2 6.  1.8]
 [5.8 2.7 4.1 1. ]
 [4.6 3.1 1.5 0.2]
 [5.7 2.5 5.  2. ]
 [6.9 3.1 4.9 1.5]
 [5.7 3.8 1.7 0.3]
 [6.4 3.1 5.5 1.8]
 [5.4 3.4 1.7 0.2]
 [5.6 2.9 3.6 1.3]
 [6.1 2.8 4.7 1.2]
 [4.8 3.1 1.6 0.2]
 [7.1 3.  5.9 2.1]
 [5.1 3.8 1.5 0.3]
 [5.4 3.7 1.5 0.2]
 [6.3 2.8 5.1 1.5]
 [6.4 3.2 4.5 1.5]
 [6.1 2.9 4.7 1.4]
 [7.7 3.  6.1 2.3]
 [5.2 3.4 1.4 0.2]
 [6.4 3.2 5.3 2.3]
 [4.8 3.  1.4 0.3]
 [5.1 3.8 1.6 0.2]
 [4.7 3.2 1.3 0.2]
 [6.7 3.1 5.6 2.4]
 [5.1 3.5 1.4 0.3]
 [5.1 3.8 1.9 0.4]
 [6.2 2.8 4.8 1.8]
 [6.6 3.  4.4 1.4]
 [5.6 2.5 3.9 1.1]], 个数: 30
测试集的标签: [2 2 1 0 2 1 0 2 0 1 1 0 2 0 0 2 1 1 2 0 2 0 0 0 2 0 0 2 1 1], 个数: 30

dm04_iris_evaluate_test()输出：