88~93感知机f

wjykp2026-01-01 8:23

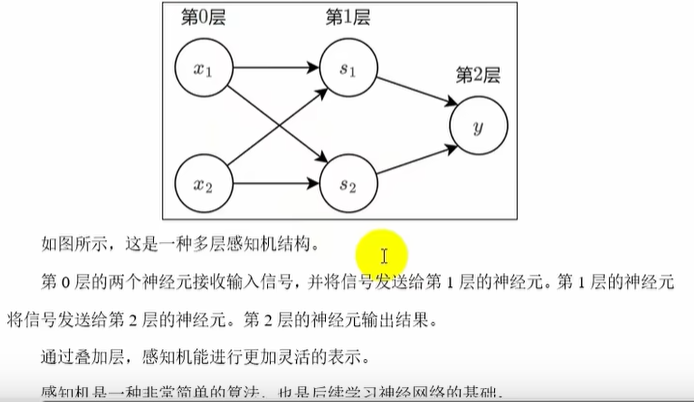
感知机的概念

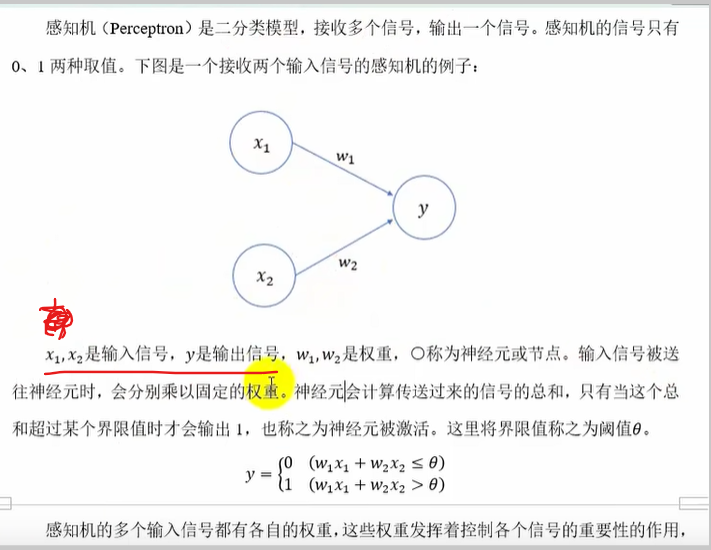
输入输出x,y都是0 or 1

简单逻辑电路

与门

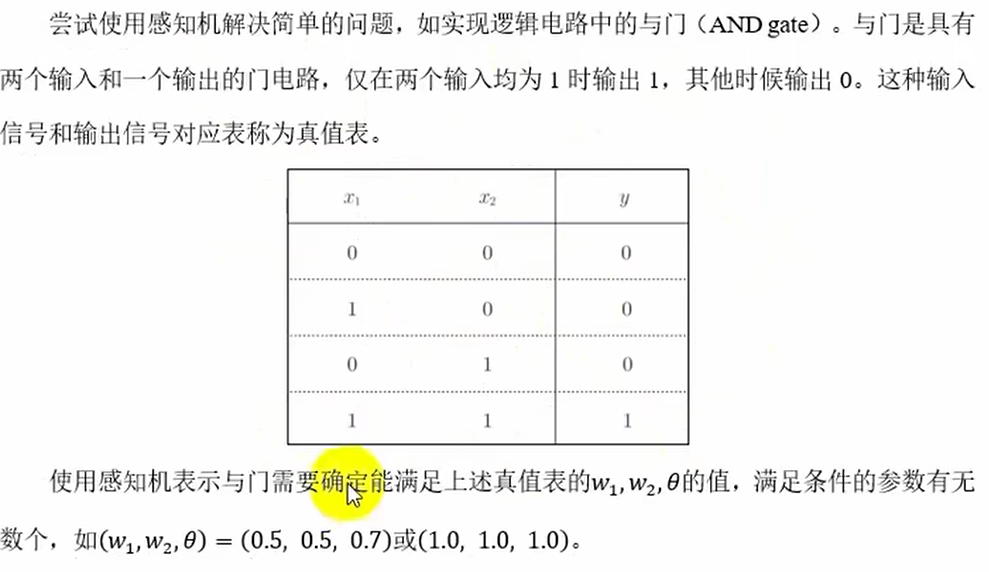
与非门

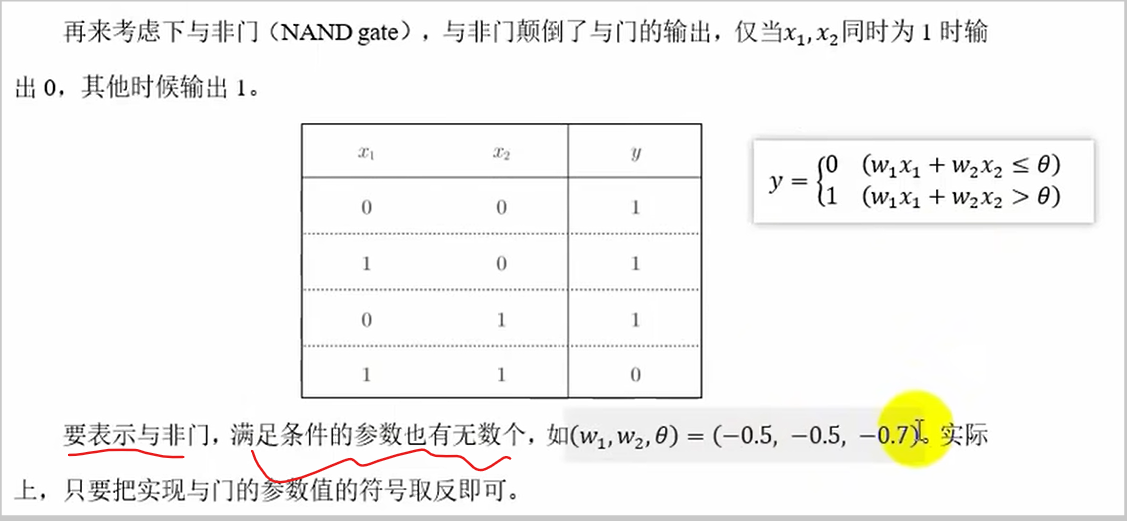
或门

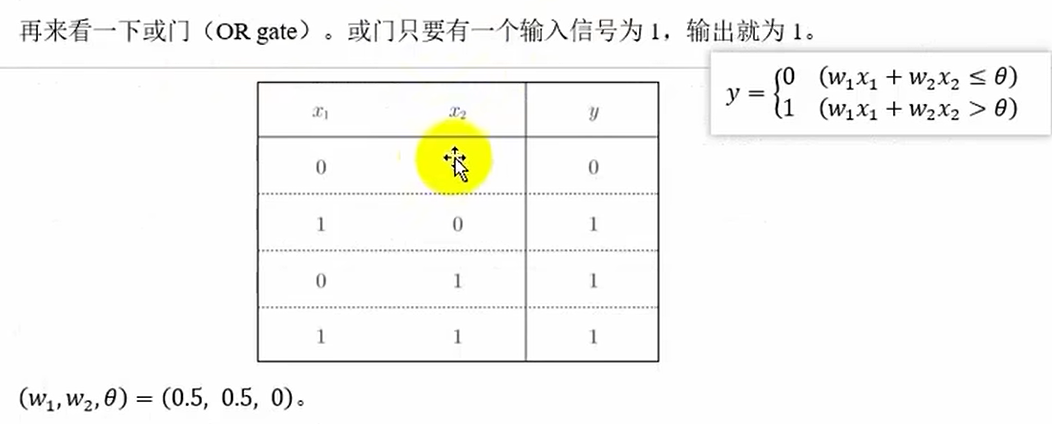
感知机的实现

导入权重和偏置

代码实现

复制代码

# 实现与门
# def AND(x1,x2):
#     w1,w2,theta=0.5,0.5,0.7
#     res=x1*w1+x2*w2
#     if res<=theta:
#         return 0
#     else:
#         return 1
import numpy as np


def AND(x1,x2):
     x=np.array([x1,x2])
     w=np.array([0.5,0.5])
     b=-0.7
     # 直接用矩阵运算的形式计算结果
     res=w@x+b
     if res<=0:
         return 0
     else:
         return 1
# 测试
print(AND(0,0))
print(AND(0,1))
print(AND(1,0))
print(AND(1,1))
# 0 0 0 1

# 与非门
def NAND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([-0.5, -0.5])
    b = 0.7
    # 直接用矩阵运算的形式计算结果
    res = w @ x + b
    if res <= 0:
        return 0
    else:
        return 1
# 测试
print(NAND(0,0))
print(NAND(0,1))
print(NAND(1,0))
print(NAND(1,1))
# 1 1 1 0

# 或门
def OR(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.2
    # 直接用矩阵运算的形式计算结果
    res = w @ x + b
    if res <= 0:
        return 0
    else:
        return 1
# 测试
print(OR(0,0))
print(OR(0,1))
print(OR(1,0))
print(OR(1,1))
# 0 1 1 1

感知机的局限

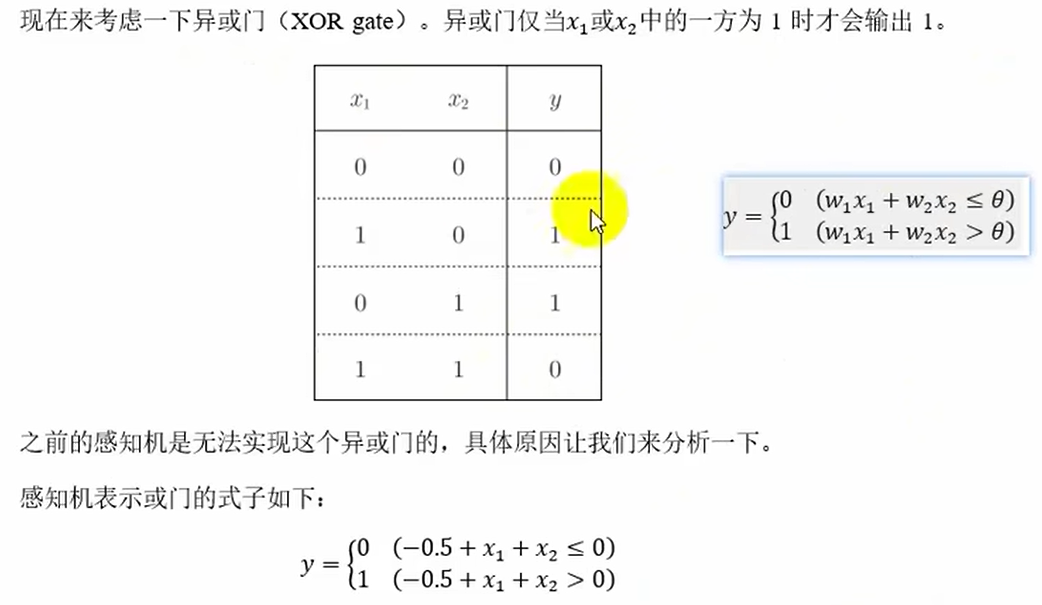
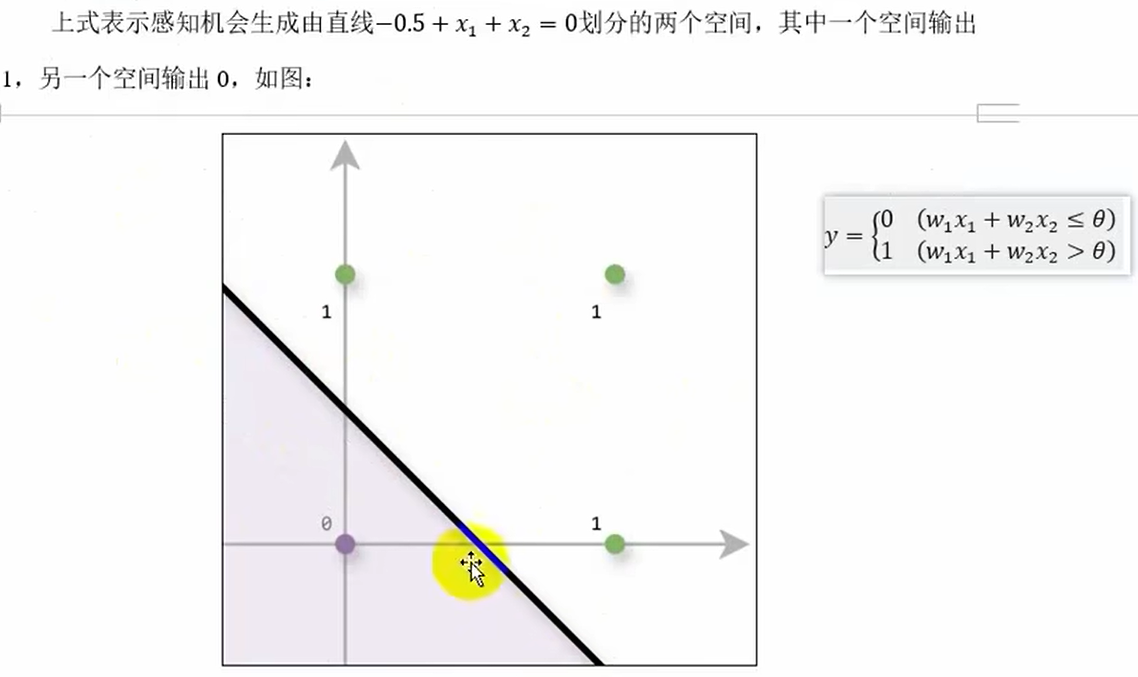
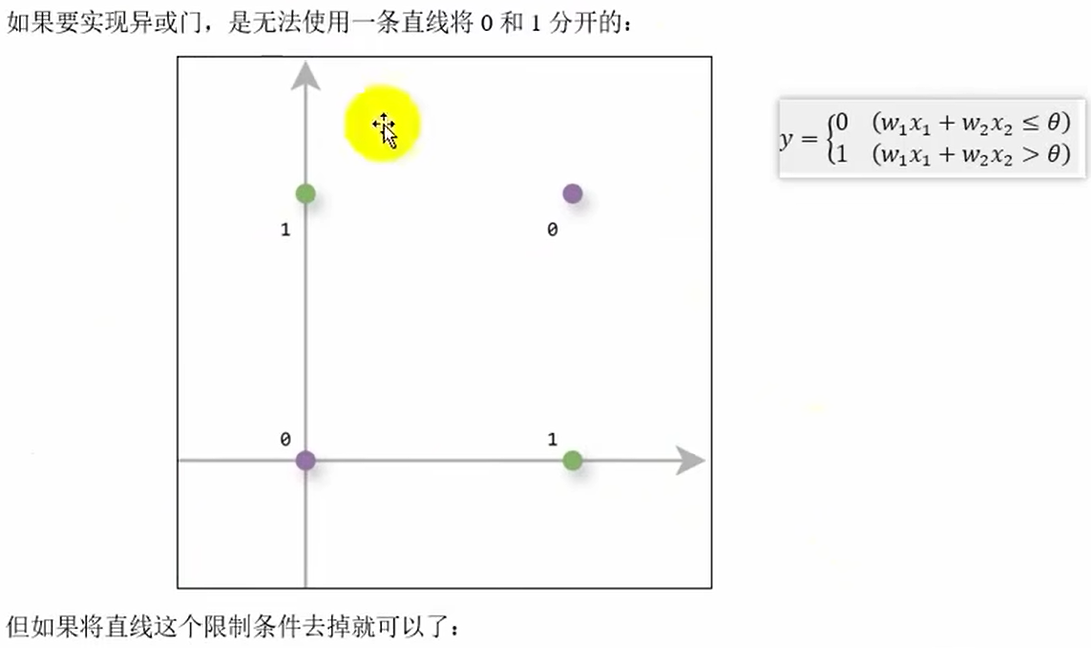
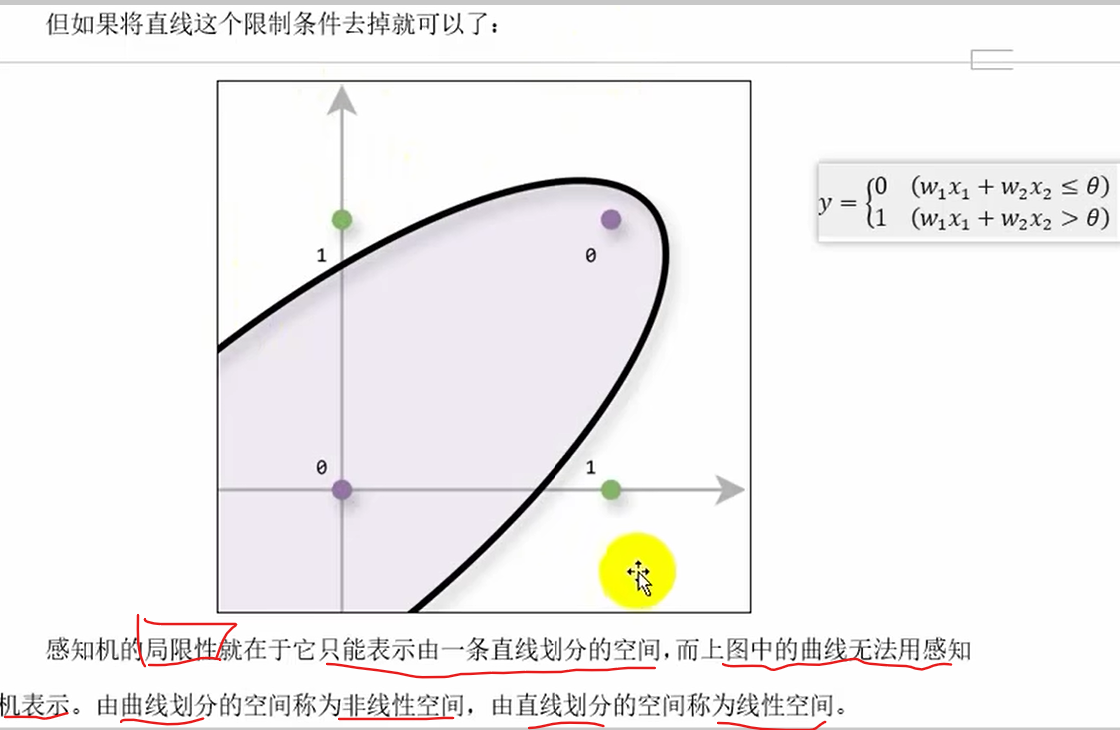
多层感知机

复制代码

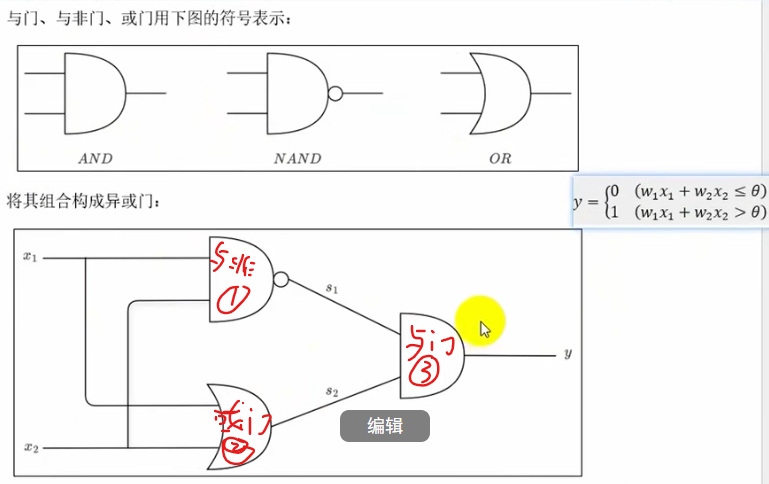
# 异或门
def XOR(x1,x2):
    s1=NAND(x1,x2)
    s2=OR(x1, x2)
    y=AND(s1, s2)
    return y
# 测试
print(XOR(0,0))
print(XOR(0,1))
print(XOR(1,0))
print(XOR(1,1))
# 0 1 1 0