大家好,从今天开始,我将在这一个专辑当中陆续给大家分享算法竞赛当中的进阶算法,大家如果对算法竞赛有兴趣的化,可以关注我一下,相信一定会给大家带来收获。
这一期,我讲给大家分享的是++树的 dfs 序++ ,一个比较简单的算法知识,但是简单归简单,它是后续较难算法的奠基石,后面很多较难的算法知识都会用到树的 dfs 序,所以是很重要的。
那么废话不多说,我们直接开始:
一:树的 dfs 序
树的 dfs 序,顾名思义,就是对一棵树进行 dfs 所得到的序列。
树的创建方式是不唯一的,树的遍历方式也是不唯一的,那么树的 dfs 序就会有很多种形式。
今天,我先来给大家介绍一种基于 "先序" 遍历形成的 dfs 序,也称作 dfn 序或者时间戳。
这种 dfs 序是指在深度优先遍历的过程中,按照访问结点的顺序给结点进行编号,如下图所示:
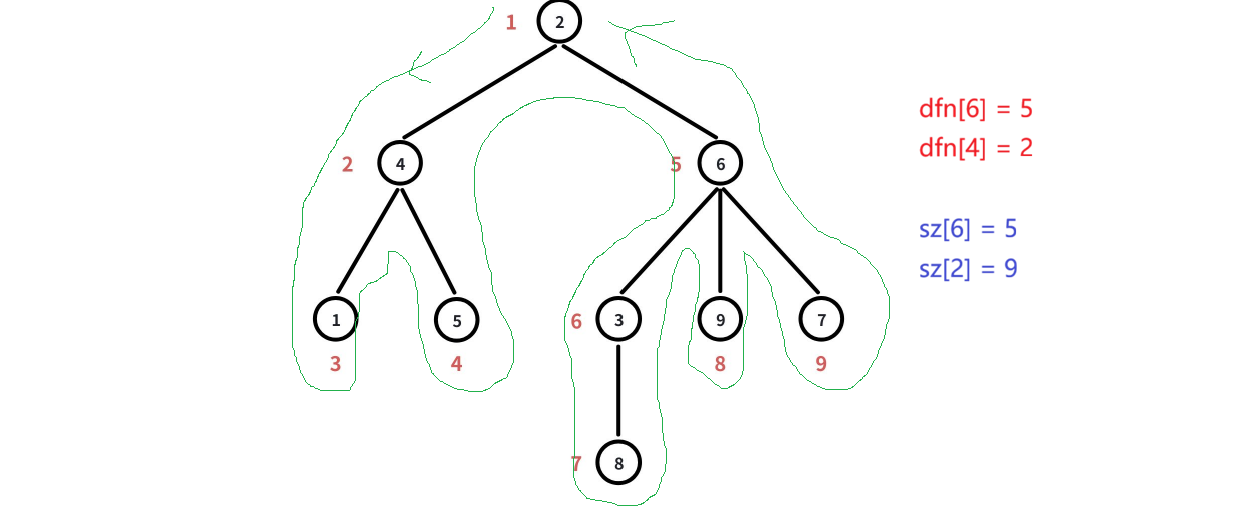
至于先遍历哪一个孩子结点,其实是无所谓的,不影响后面的性质。
二:代码实现
我们要编写代码求出一棵树的 dfn 序:
1. idx 表示新遍历到一个结点,它在 dfn 序中的编号。
2. dfn[x] 表示:x 结点的 dfn 序。(一次 dfs 就可以维护出来)
3. sz[x] 表示:以 x 为根的子树的大小(树形 dp 就可以维护出来)(后面有用)
cpp
vector<int> edges[N];
int dfn[N], sz[N], idx; // dfs 序,子树的大小
void dfs(int x, int fa)
{
dfn[x] = ++idx;
sz[x] = 1;
for(auto y : edges[x])
{
if(y == fa) continue;
dfs(y, x)
sz[x] += sz[y];
}
} 三:性质
性质 1:
在一棵子树中,dfn 序是连续的。(通过 dfs 的过程就可以证明其正确性)
性质 2:
祖先节点的 dfn 序小于子孙节点的 dfn 序。(通过 dfs 的过程就可以证明其正确性)
性质 3:
以 x 为根的子树中,dfn 序为 [dfn[x], dfn[x] + sz[x] - 1](通过 dfs 的过程就可以证明其正确性)
上面所列的三个性质只需要记住结论就可以了,如果实在不好理解的话,就画图看一看:
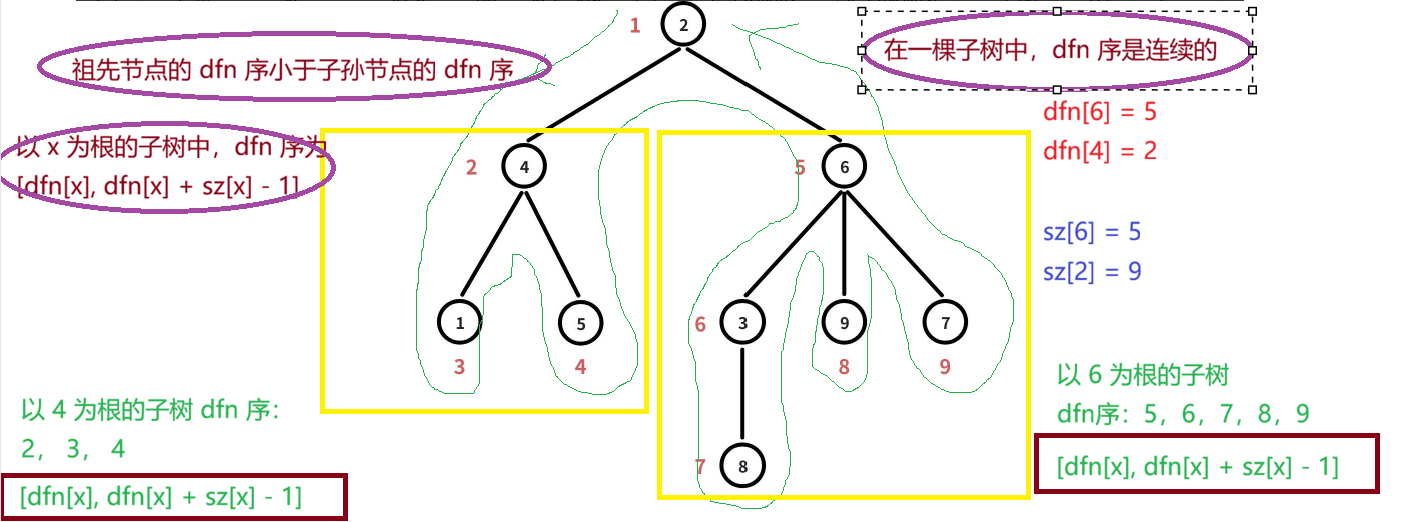
四:应用
应用 1:
如何判断结点 y 是否在以结点 x 为根的子树中???
在我们没有学习树的 dfn 序之前,我们的做法是:
在 dfs 的过程中,维护出每一个结点的父亲结点信息 fa 数组。然后以 y 结点为起点,一直向上找 x,如果能找到,则说明结点 y 在以结点 x 为根的子树中,否则,结点 y 不在以结点 x 为根的子树中。
这样的话,单次判断的时间复杂度就会达到 O(n)。
如果是q** 次判断,时间复杂度就会达到 O(n * q)。**
我们学习完树的 dfn 序之后,就有更高效的解法了:
我们可以通过一次 dfs 预处理出 dfn 数组。然后每一次判断,就去看一下 dfn[y] 是否在
[dfn[x], dfn[x] + sz[x] - 1] 中就可以了。
这样的话,预处理的时间复杂度为 O(n),q 次询问的时间复杂度为 O(q)。
整体时间复杂度就为 O(n + q)(线性级别)了。
应用 2:
在一些树上问题中,利用树的 dfs 序,可以将 "树上问题" 转变成 "序列问题"。
比如说:
将以 x 为根的子树,所有的结点权值全部加 1,对应的就是将序列**[dfn[x], dfn[x] + sz[x] - 1] 中的元素全部增加 1。**
树上问题转化成为序列问题,我们就可以用之前学过的各种数据结构(线段树、树状数组......)来维护这些信息了。
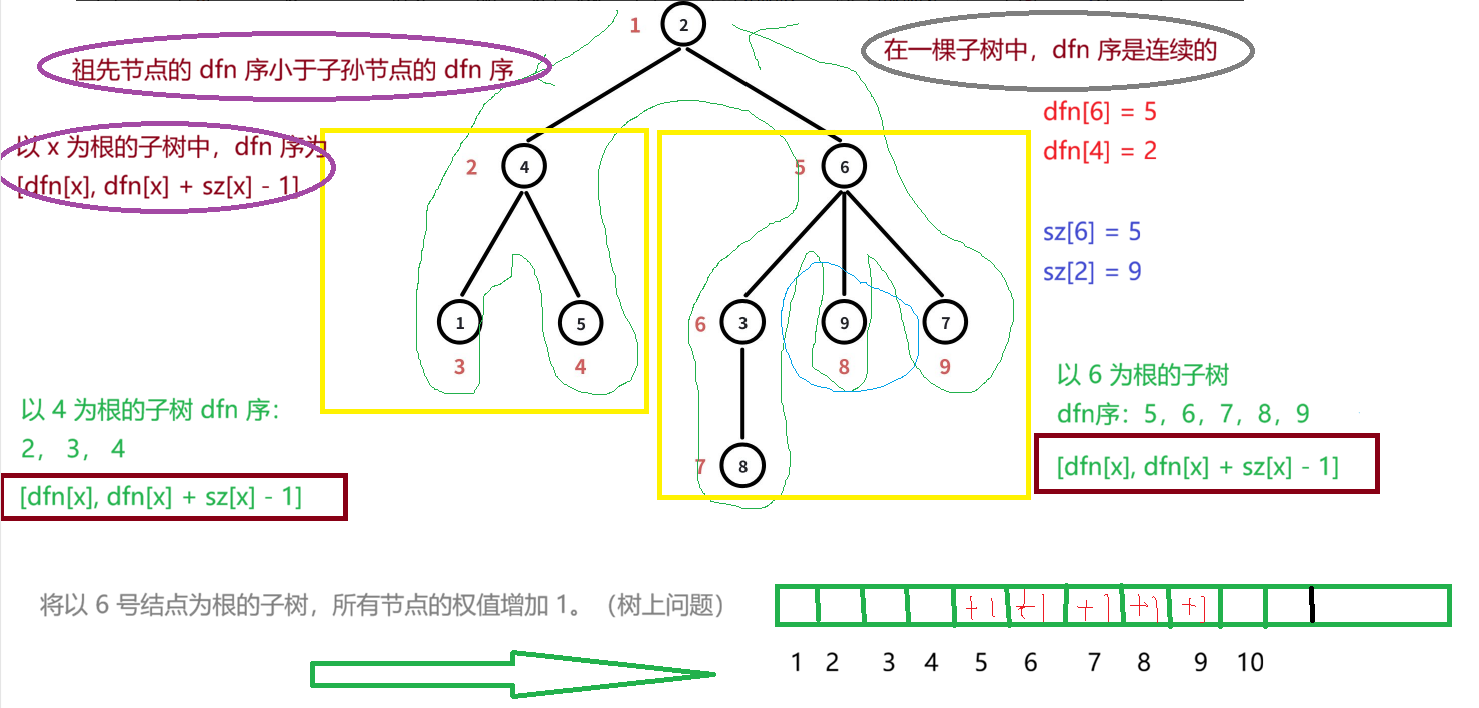
五:模板题
接下来就是两道关于树的 dfs 序的**模板题目,**大家既然已经看到了这里,还是希望大家自己先尝试一下,看看能不能解决,再去对照我的代码。
题目链接:题目一:DFS 序 1 题目二:DFS 序 2
题目描述 + 算法原理:
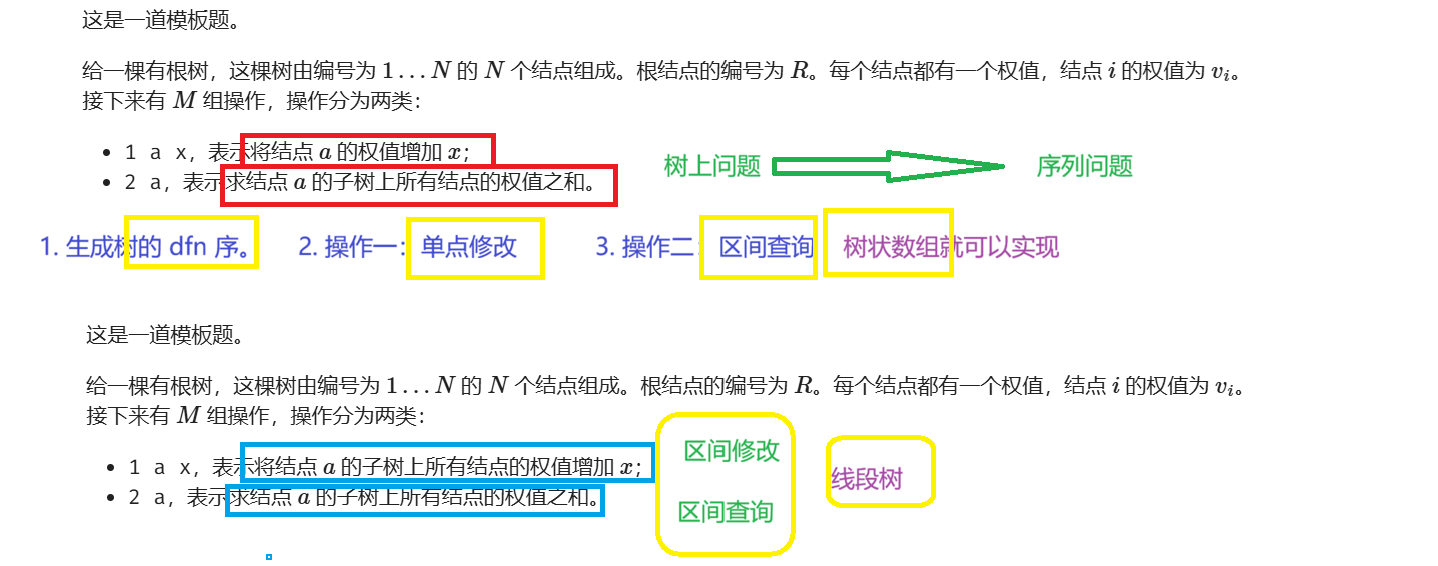
代码实现:
题目一:DFS 序 1:
cpp
#include <iostream>
#include <vector>
using namespace std;
#define lowbit(x) (x & -x)
typedef long long LL;
const int N = 1e6 + 10;
int n, m, r, a[N];
vector<int> edges[N];
int dfn[N], sz[N], idx;
LL s[N]; // 树状数组
void modify(int x, LL k)
{
for(int i = x; i <= n; i += lowbit(i)) s[i] += k;
}
LL query(int x)
{
LL sum = 0;
for(int i = x; i; i -= lowbit(i)) sum += s[i];
return sum;
}
void dfs(int x, int fa)
{
dfn[x] = ++idx;
sz[x] = 1;
modify(dfn[x], a[x]); // 初始的权值
for(auto y : edges[x])
{
if(y == fa) continue;
dfs(y, x);
sz[x] += sz[y];
}
}
int main()
{
cin >> n >> m >> r;
for(int i = 1; i <= n; i++) cin >> a[i];
for(int i = 1; i < n; i++)
{
int x, y; cin >> x >> y;
edges[x].push_back(y);
edges[y].push_back(x);
}
dfs(r, 0);
while(m--)
{
int op, a, x; cin >> op >> a;
if(op == 1)
{
cin >> x;
modify(dfn[a], x);
}
else
{
int l = dfn[a], r = dfn[a] + sz[a] - 1;
cout << query(r) - query(l - 1) << endl;
}
}
return 0;
} 题目二:DFS 序 2:
cpp
#include <iostream>
#include <vector>
using namespace std;
#define lc p << 1
#define rc p << 1 | 1
typedef long long LL;
const int N = 1e6 + 10;
int n, m, r, a[N];
vector<int> edges[N];
int dfn[N], sz[N], rnk[N], idx;
struct node
{
int l, r;
LL sum, add;
}tr[N << 2];
void dfs(int x, int fa)
{
dfn[x] = ++idx;
rnk[idx] = x;
sz[x] = 1;
for(auto y : edges[x])
{
if(y == fa) continue;
dfs(y, x);
sz[x] += sz[y];
}
}
void pushup(int p)
{
tr[p].sum = tr[lc].sum + tr[rc].sum;
}
void build(int p, int l, int r)
{
tr[p] = {l, r, a[rnk[l]], 0};
if(l == r) return;
int mid = (l + r) / 2;
build(lc, l, mid); build(rc, mid + 1, r);
pushup(p);
}
void lazy(int p, LL k)
{
tr[p].sum += (tr[p].r - tr[p].l + 1) * k;
tr[p].add += k;
}
void pushdown(int p)
{
if(tr[p].add)
{
lazy(lc, tr[p].add);
lazy(rc, tr[p].add);
tr[p].add = 0;
}
}
void modify(int p, int x, int y, LL k)
{
int l = tr[p].l, r = tr[p].r;
if(x <= l && r <= y)
{
lazy(p, k);
return;
}
pushdown(p);
int mid = (l + r) >> 1;
if(x <= mid) modify(lc, x, y, k);
if(y > mid) modify(rc, x, y, k);
pushup(p);
}
LL query(int p, int x, int y)
{
int l = tr[p].l, r = tr[p].r;
if(x <= l && r <= y) return tr[p].sum;
pushdown(p);
int mid = (l + r) >> 1;
LL s = 0;
if(x <= mid) s += query(lc, x, y);
if(y > mid) s += query(rc, x, y);
return s;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin >> n >> m >> r;
for(int i = 1; i <= n; i++) cin >> a[i];
for(int i = 1; i < n; i++)
{
int a, b; cin >> a >> b;
edges[a].push_back(b);
edges[b].push_back(a);
}
dfs(r, 0);
build(1, 1, n);
while(m--)
{
int op, a, x; cin >> op >> a;
int l = dfn[a], r = dfn[a] + sz[a] - 1;
if(op == 1)
{
cin >> x;
modify(1, l, r, x);
}
else
{
cout << query(1, l, r) << endl;
}
}
return 0;
}好的,今天的分享就到这里了,看到最后的你是不是收获慢慢呢~~~,
如果是的话,别忘了一键三连哦~~~
如果还是有问题的话,可以下来和我交流,或者直接在评论区指明。
谢谢大家的观看,我们下一期再见。