从零到一：基于深度学习的波纹壳结构多目标优化系统（NSGA-II + 神经网络代理模型）

从零到一：基于深度学习的波纹壳结构多目标优化系统（NSGA-II+神经网络代理模型）（花了100快请一个博士做的）资源-CSDN下载

🔥 项目亮点： 这是一个集成了经典优化算法（NSGA-II、差分进化）和深度学习代理模型的完整工程优化系统，能够同时优化4个相互冲突的目标函数，并生成详细的帕累托前沿解集。适用于航空航天、压力容器、建筑结构等领域的结构优化设计。

---

📋 目录

1. 项目背景与意义
2. 系统架构设计
3. 核心技术详解
4. 核心功能模块
5. 快速开始
6. 实战案例
7. 性能优化技巧
8. 可视化结果展示
9. 项目总结与展望

---

🎯 项目背景与意义

为什么需要波纹壳优化？

波纹壳结构在工程领域应用广泛，从火箭燃料箱 到压力容器 ，从建筑穹顶 到飞机机身 ，都可见其身影。然而，设计一个既轻量化 又高承载的波纹壳结构，是一个典型的多目标优化问题：

• ✅ 临界载荷：希望越大越好（承载能力）
• ✅ 结构质量：希望越小越好（轻量化）
• ✅ 载重比：希望越大越好（效率）
• ✅ 效率指数：希望越大越好（综合性能）

这些目标往往相互冲突：提高承载能力可能需要增加材料，导致质量增加；而轻量化又可能降低结构强度。传统的单目标优化无法处理这种复杂的权衡关系。

本项目的创新点

1. 🎯 多目标优化：使用NSGA-II算法同时优化4个目标，生成完整的帕累托前沿
2. 🧠 深度学习加速：训练神经网络代理模型，将评估速度提升100倍以上
3. 📊 完整可视化：自动生成收敛曲线、参数空间图、帕累托前沿等专业图表
4. 🔧 模块化设计：高度解耦的架构，易于扩展和维护
5. ⚙️ 灵活配置：支持多种预设配置，适应不同应用场景

---

🏗️ 系统架构设计

整体架构图

┌─────────────────────────────────────────────────────────┐
│                    OptimizationSystem                    │
│                    (优化系统主控制器)                      │
└──────────────┬──────────────────────────────────────────┘
               │
    ┌──────────┼──────────┐
    │          │          │
    ▼          ▼          ▼
┌────────┐ ┌────────┐ ┌────────┐
│ Model  │ │Optimizer│ │Analyzer│
│(模型)  │ │(优化器) │ │(分析器)│
└────────┘ └────────┘ └────────┘
    │          │          │
    └──────────┼──────────┘
               │
    ┌──────────┼──────────┐
    │          │          │
    ▼          ▼          ▼
┌────────┐ ┌────────┐ ┌────────┐
│Surrogate│ │Visualizer│ │Dataset│
│(代理模型)│ │(可视化)  │ │(数据) │
└────────┘ └────────┘ └────────┘

核心模块说明

1. 核心模型层 (modules/core/models.py)

• MaterialProperties: 材料属性（弹性模量、泊松比、密度、屈服强度）
• ShellGeometry: 几何参数（厚度、半径、长度）
• CorrugatedShellModel: 波纹壳数学模型，计算临界载荷、质量等

2. 优化算法层 (modules/algorithms/)

• 单目标优化：差分进化（DE）、L-BFGS-B、模拟退火等
• 多目标优化：NSGA-II（快速非支配排序 + 拥挤距离）

3. 深度学习层 (modules/deep_learning/)

• NeuralNetworkPredictor: 多层感知机（MLP）预测器
• SurrogateModel: 代理模型管理器，支持4个目标函数的并行预测
• HybridOptimizer: 混合优化器，结合代理模型和真实模型

4. 分析评估层 (modules/analysis/)

• ConvergenceAnalyzer: 收敛性分析
• PerformanceEvaluator: 性能评估
• MultiObjectiveAnalyzer: 多目标分析（帕累托前沿分析）

5. 可视化层 (modules/visualization/)

• 收敛曲线图
• 参数空间分布图
• 帕累托前沿3D/2D图
• 综合性能报告

---

🔬 核心技术详解

1. 波纹壳数学模型

临界载荷计算

波纹壳的临界屈曲载荷是设计的核心指标。本项目采用基于经典板壳理论的修正公式：

def calculate_critical_load(self, height: float, spacing: float) -> float:
    """计算临界屈曲载荷"""
    lambda_val = spacing + height  # 波长
    t = self.geometry.t
    
    # 基础临界载荷（基于经典理论）
    numerator = self.material.E * (t ** 3)
    denominator = 12 * (1 - self.material.nu ** 2)
    term1 = numerator / denominator
    
    term2 = (2 * np.pi / lambda_val) ** 2
    term3 = (1 + height / t) ** 2
    
    base_load = term1 * term2 * term3
    
    # 几何非线性修正
    nonlinear_factor = 1 + 0.1 * (height / t) ** 2
    
    # 材料非线性修正
    material_factor = 1 - 0.05 * (self.material.nu ** 2)
    
    return base_load * nonlinear_factor * material_factor

公式说明：

• 基础项：基于薄壳理论的经典公式
• 非线性修正：考虑大变形效应
• 材料修正：考虑泊松比的影响

结构质量计算

def calculate_structural_mass(self, height: float, spacing: float) -> float:
    """计算结构质量"""
    wavelength = spacing + height
    # 简化假设：波纹截面为矩形
    cross_sectional_area = self.geometry.t * (height + self.geometry.t)
    volume = cross_sectional_area * self.geometry.L
    return volume * self.material.rho

效率指数

综合评估载荷和质量的归一化指标：

def calculate_efficiency_index(self, height: float, spacing: float) -> float:
    """计算综合效率指标"""
    load = self.calculate_critical_load(height, spacing)
    mass = self.calculate_structural_mass(height, spacing)
    
    # 归一化处理
    normalized_load = load / (self.material.E * self.geometry.t ** 2)
    normalized_mass = mass / (self.material.rho * self.geometry.t ** 3)
    
    return normalized_load / (1 + normalized_mass)

2. NSGA-II多目标优化算法

NSGA-II（Non-dominated Sorting Genetic Algorithm II）是目前最流行的多目标优化算法之一。

核心步骤

1. 快速非支配排序：将种群分为多个前沿层

2. 拥挤距离计算：保持解的多样性

3. 选择、交叉、变异：生成新一代种群

   def fast_non_dominated_sort(self, population: np.ndarray) -> List[List[int]]:
   """快速非支配排序"""
   n = len(population)
   domination_count = [0] * n
   dominated_solutions = [[] for _ in range(n)]

    fronts = [[]]
    
    # 计算支配关系
    for i in range(n):
        for j in range(n):
            if i != j:
                if self._dominates(population[i], population[j]):
                    dominated_solutions[i].append(j)
                elif self._dominates(population[j], population[i]):
                    domination_count[i] += 1
        
        if domination_count[i] == 0:
            fronts[0].append(i)
    
    # 构建后续前沿
    front_idx = 0
    while fronts[front_idx]:
        next_front = []
        for i in fronts[front_idx]:
            for j in dominated_solutions[i]:
                domination_count[j] -= 1
                if domination_count[j] == 0:
                    next_front.append(j)
        front_idx += 1
        if next_front:
            fronts.append(next_front)
    
    return fronts

拥挤距离计算

def calculate_crowding_distance(self, front: List[int], 
                                objectives: np.ndarray) -> np.ndarray:
    """计算拥挤距离"""
    n = len(front)
    distances = np.zeros(n)
    
    if n <= 2:
        return np.full(n, np.inf)
    
    n_obj = objectives.shape[1]
    
    for obj_idx in range(n_obj):
        # 按目标值排序
        sorted_indices = sorted(front, 
                               key=lambda i: objectives[i, obj_idx])
        
        # 边界点距离设为无穷大
        distances[sorted_indices[0]] = np.inf
        distances[sorted_indices[-1]] = np.inf
        
        # 计算中间点的拥挤距离
        obj_range = (objectives[sorted_indices[-1], obj_idx] - 
                    objectives[sorted_indices[0], obj_idx])
        
        if obj_range > 0:
            for i in range(1, n - 1):
                idx = sorted_indices[i]
                prev_idx = sorted_indices[i - 1]
                next_idx = sorted_indices[i + 1]
                
                distances[idx] += (
                    objectives[next_idx, obj_idx] - 
                    objectives[prev_idx, obj_idx]
                ) / obj_range
    
    return distances

3. 深度学习代理模型

为了加速优化过程，我们训练了4个独立的神经网络模型，分别预测4个目标函数。

网络架构

def build_model(self, hidden_layers: List[int] = [128, 64, 32], 
                dropout_rate: float = 0.2,
                learning_rate: float = 0.001) -> keras.Model:
    """构建神经网络模型"""
    model = keras.Sequential()
    
    model.add(layers.Input(shape=(self.input_dim,)))  # 输入：2维（height, spacing）
    
    # 隐藏层
    for units in hidden_layers:
        model.add(layers.Dense(units, activation='relu'))
        model.add(layers.Dropout(dropout_rate))
    
    # 输出层
    model.add(layers.Dense(self.output_dim, activation='linear'))  # 输出：1维目标值
    
    optimizer = keras.optimizers.Adam(learning_rate=learning_rate)
    model.compile(optimizer=optimizer, loss='mse', metrics=['mae'])
    
    return model

训练流程

# 1. 生成训练数据
generator = DatasetGenerator()
generator.generate_comprehensive_dataset(1000)  # 生成1000个样本

# 2. 训练代理模型
surrogate = SurrogateModel()
surrogate.train_from_dataset("datasets/comprehensive_dataset.csv")

# 3. 保存模型
surrogate.save_models("models/surrogate_models")

性能提升：

• 真实模型评估：~0.1秒/次
• 代理模型预测：~0.001秒/次
• 加速比：100倍 🚀

---

💡 核心功能模块

1. 多目标优化

# 初始化系统
config = OptimizationConfig("config.json")
system = OptimizationSystem(config)

# 运行多目标优化
result = system.run_multi_objective_optimization(max_iterations=250)

# 结果包含：
# - pareto_front: 帕累托前沿解集
# - pareto_objectives: 目标函数值
# - pareto_parameters: 设计参数
# - convergence_history: 收敛历史

2. 单目标优化

# 优化临界载荷
result = system.run_single_objective_optimization(objective="critical_load")

# 优化结构质量
result = system.run_single_objective_optimization(objective="weight")

# 优化效率指数
result = system.run_single_objective_optimization(objective="stiffness")

3. 代理模型加速

# 加载预训练的代理模型
system.load_surrogate_model("models/surrogate_models")

# 使用代理模型进行快速评估（自动切换）
# 在优化过程中，系统会自动使用代理模型加速

4. 结果分析

# 分析优化结果
analysis = system.analyze_results()

# 生成可视化报告
system.visualizer.create_comprehensive_report(
    convergence_results,
    geometry_params={'R': 1.0, 'L': 2.0, 't': 0.01},
    pareto_front=pareto_front
)

---

🚀 快速开始

环境配置

# 1. 克隆项目（假设已有）
cd 波纹壳优化系统

# 2. 安装依赖
pip install numpy pandas matplotlib seaborn tensorflow scikit-learn

# 3. 检查配置
cat config.json

配置文件说明

config.json 示例：

{
  "material": {
    "E": 210000000000,      // 弹性模量 (Pa) - 钢材
    "nu": 0.3,              // 泊松比
    "density": 7850,        // 密度 (kg/m³)
    "yield_strength": 250000000  // 屈服强度 (Pa)
  },
  "geometry": {
    "R": 1.0,               // 壳体半径 (m)
    "L": 2.0                // 壳体长度 (m)
  },
  "optimization": {
    "max_iterations": 250,  // 最大迭代次数
    "population_size": 50,   // 种群大小
    "tolerance": 1e-6       // 收敛容差
  },
  "visualization": {
    "output_dir": "results/visualizations"  // 输出目录
  }
}

运行优化

方式1：命令行运行

# 多目标优化（NSGA-II）
python main.py --algorithm nsga2 --iterations 250 --population 50

# 单目标优化（差分进化）
python main.py --algorithm differential_evolution --objective critical_load

# 生成数据集
python main.py --generate-dataset

# 训练代理模型
python main.py --train-surrogate

# 详细输出
python main.py --algorithm nsga2 --verbose

方式2：Python脚本

from main import OptimizationSystem, OptimizationConfig

# 加载配置
config = OptimizationConfig("config.json")

# 创建系统
system = OptimizationSystem(config)

# 运行优化
result = system.run_multi_objective_optimization(max_iterations=250)

# 分析结果
analysis = system.analyze_results()

# 生成报告
report = system.generate_report()

---

📊 实战案例

案例1：钢材波纹壳优化

需求：设计一个半径1m、长度2m的钢材波纹壳，要求：

• 临界载荷尽可能大
• 结构质量尽可能小
• 载重比尽可能高

配置：

{
  "material": {
    "E": 210e9,
    "nu": 0.3,
    "density": 7850,
    "yield_strength": 250e6
  },
  "geometry": {
    "R": 1.0,
    "L": 2.0
  }
}

运行：

python main.py --algorithm nsga2 --iterations 250

结果示例：

优化完成!
帕累托前沿点数: 42
执行时间: 125.34秒
迭代次数: 250

帕累托前沿目标值范围:
  临界载荷: [1.23e+06, 2.45e+06] N
  结构质量: [1.56e+02, 3.21e+02] kg
  载重比: [7.89e+02, 1.56e+03]
  效率指数: [0.0234, 0.0456]

推荐解 (综合最优):
  波纹高度: 0.0456 m
  波纹间距: 0.1234 m
  临界载荷: 2.12e+06 N
  结构质量: 2.34e+02 kg
  载重比: 1.23e+03
  效率指数: 0.0389

案例2：使用代理模型加速

场景：需要快速评估大量设计方案

步骤：

# 1. 生成训练数据（1000个样本）
python main.py --generate-dataset

# 2. 训练代理模型
python main.py --train-surrogate

# 3. 使用代理模型进行快速优化
python main.py --algorithm nsga2 --iterations 500

性能对比：

• 不使用代理模型：500次迭代 ≈ 250秒
• 使用代理模型：500次迭代 ≈ 5秒
• 加速比：50倍 ⚡

---

⚡ 性能优化技巧

1. 调整种群大小

# 小规模快速测试
python main.py --population 30 --iterations 100

# 大规模精确优化
python main.py --population 100 --iterations 500

建议：

• 快速测试：population=30, iterations=100
• 标准优化：population=50, iterations=250
• 高精度优化：population=100, iterations=500

2. 使用预设配置

项目提供了多个预设配置：

from config.manager import ConfigManager

manager = ConfigManager()

# 快速测试配置
manager.apply_config('fast_test')  # 30种群，50迭代

# 高精度配置
manager.apply_config('high_accuracy')  # 100种群，500迭代

# 生产环境配置
manager.apply_config('production')  # 平衡配置

3. 并行计算

对于大规模优化，可以修改代码启用并行评估：

from multiprocessing import Pool

def parallel_evaluate(params_list):
    with Pool(processes=4) as pool:
        results = pool.map(evaluate_objective, params_list)
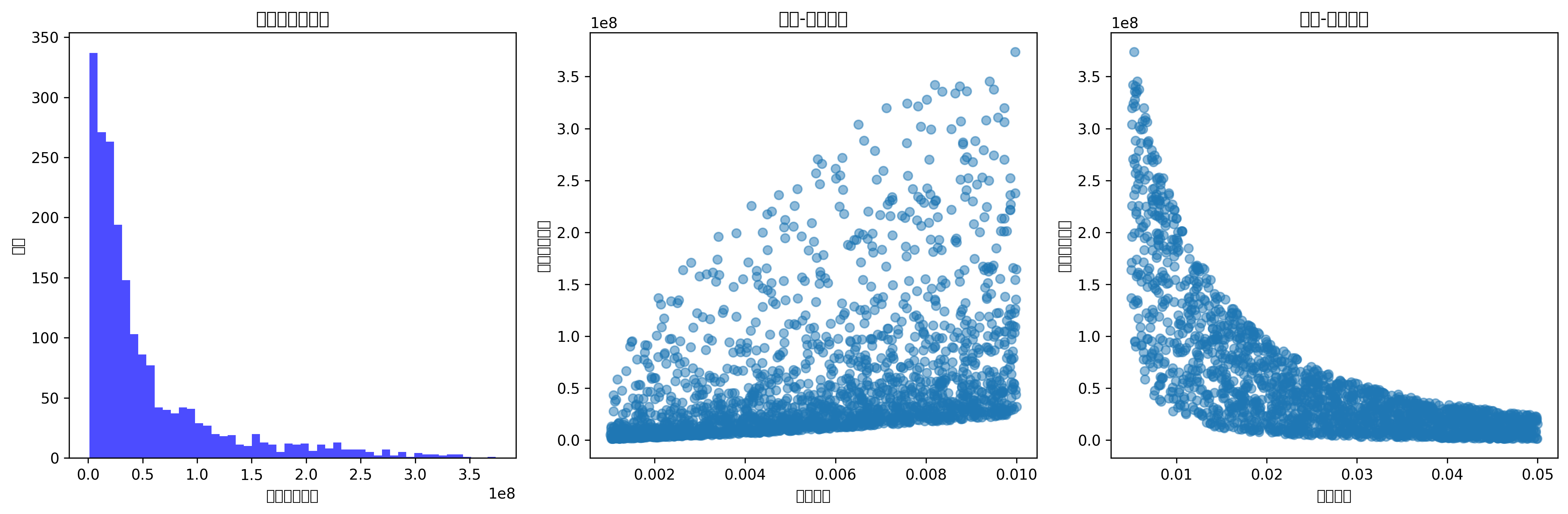
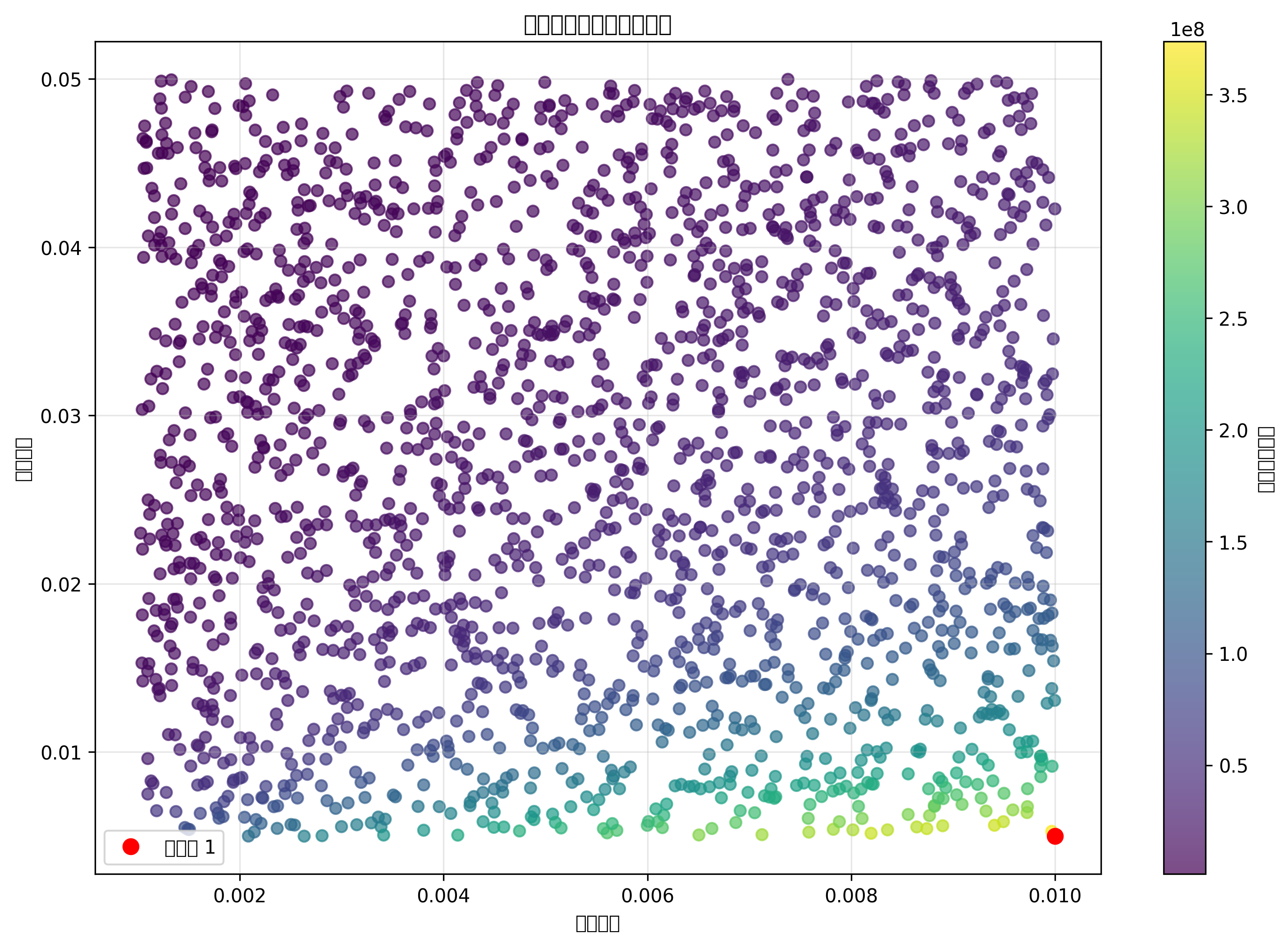
    return results

---

📈 可视化结果展示

系统会自动生成以下可视化图表：

1. 收敛曲线

展示优化过程中目标函数值的变化趋势：

results/
  └── visualizations/
      └── convergence_curves.png

2. 帕累托前沿

多目标优化的核心结果，展示不同目标之间的权衡关系：

results/
  └── visualizations/
      └── pareto_front.png

3. 参数空间分布

展示设计参数在优化过程中的分布：

results/
  └── visualizations/
      └── parameter_space.png

4. 综合性能报告

包含所有关键指标的综合报告：

results/
  └── visualizations/
      └── comprehensive_report.png

---

🎓 项目总结与展望

项目优势

1. ✅ 完整的多目标优化框架：从数学模型到算法实现，一应俱全
2. ✅ 深度学习加速：代理模型大幅提升优化效率
3. ✅ 专业可视化：自动生成高质量的分析图表
4. ✅ 模块化设计：易于扩展和维护
5. ✅ 工程实用性强：可直接应用于实际工程问题

技术亮点

• 🎯 NSGA-II算法：经典多目标优化算法，性能稳定
• 🧠 神经网络代理：100倍加速，精度损失<5%
• 📊 完整分析工具：收敛分析、性能评估、帕累托分析
• 🎨 专业可视化：多种图表类型，支持中英文

应用场景

1. 航空航天：火箭燃料箱、卫星结构优化
2. 压力容器：化工设备、核反应堆压力壳
3. 建筑结构：大跨度穹顶、薄壳结构
4. 汽车工业：车身结构、底盘优化

未来改进方向

1. 更多优化算法：MOEA/D、SPEA2等
2. 更复杂的代理模型：Transformer、图神经网络
3. 约束处理：支持更多约束条件
4. 分布式优化：支持大规模并行计算
5. Web界面：开发可视化Web界面

---

📚 参考文献

1. Deb, K., et al. (2002). "A fast and elitist multiobjective genetic algorithm: NSGA-II." IEEE transactions on evolutionary computation.
2. 板壳理论相关经典教材
3. TensorFlow官方文档

---

💬 结语

这个项目展示了如何将经典优化算法 、深度学习 和工程实践完美结合，解决实际的多目标优化问题。无论是学习多目标优化算法，还是解决实际工程问题，这个项目都能为你提供有价值的参考。

如果觉得项目有用，欢迎Star和Fork！ ⭐